文档内容
格致课堂
8.6.3 平面与平面垂直
第1课时 平面与平面垂直的判定
(用时45分钟)
【选题明细表】
知识点、方法 题号
判定定理的理解及应用 1,3,6,7
二面角 2,4,9
综合应用 5,8,10,11,12
基础巩固
1.在长方体 的侧面中,与平面ABCD垂直的平面有( )个
A.1个 B.2个 C.3个 D.4个
【答案】D
【解析】如图
在长方体中,侧棱与底面都是垂直的,所以侧面与底面ABCD垂直.
平面 、平面 、平面 、平面 均与平面ABCD垂直.
故选:D
2.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角的关系是( )
A.相等 B.互补 C.相等或互补 D.不确定
【答案】D
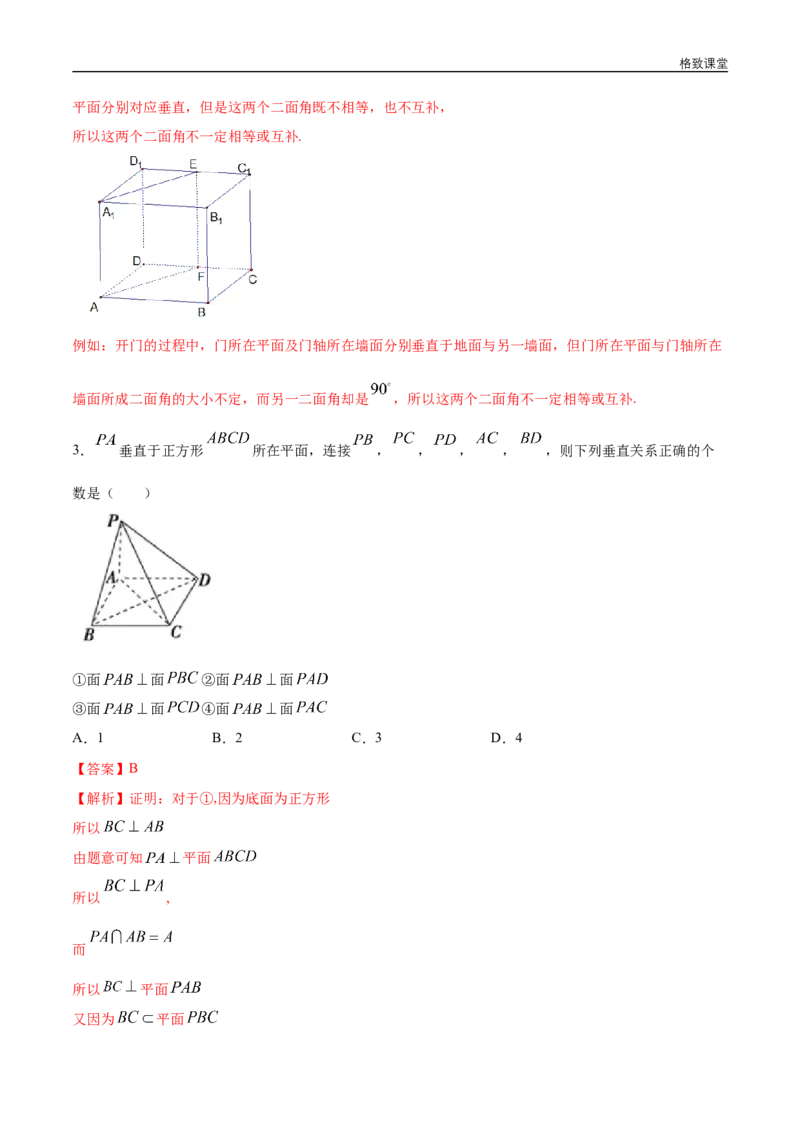
【解析】如图所示,在正方体 中,二面角 与二面角 的两个半格致课堂
平面分别对应垂直,但是这两个二面角既不相等,也不互补,
所以这两个二面角不一定相等或互补.
例如:开门的过程中,门所在平面及门轴所在墙面分别垂直于地面与另一墙面,但门所在平面与门轴所在
墙面所成二面角的大小不定,而另一二面角却是 ,所以这两个二面角不一定相等或互补.
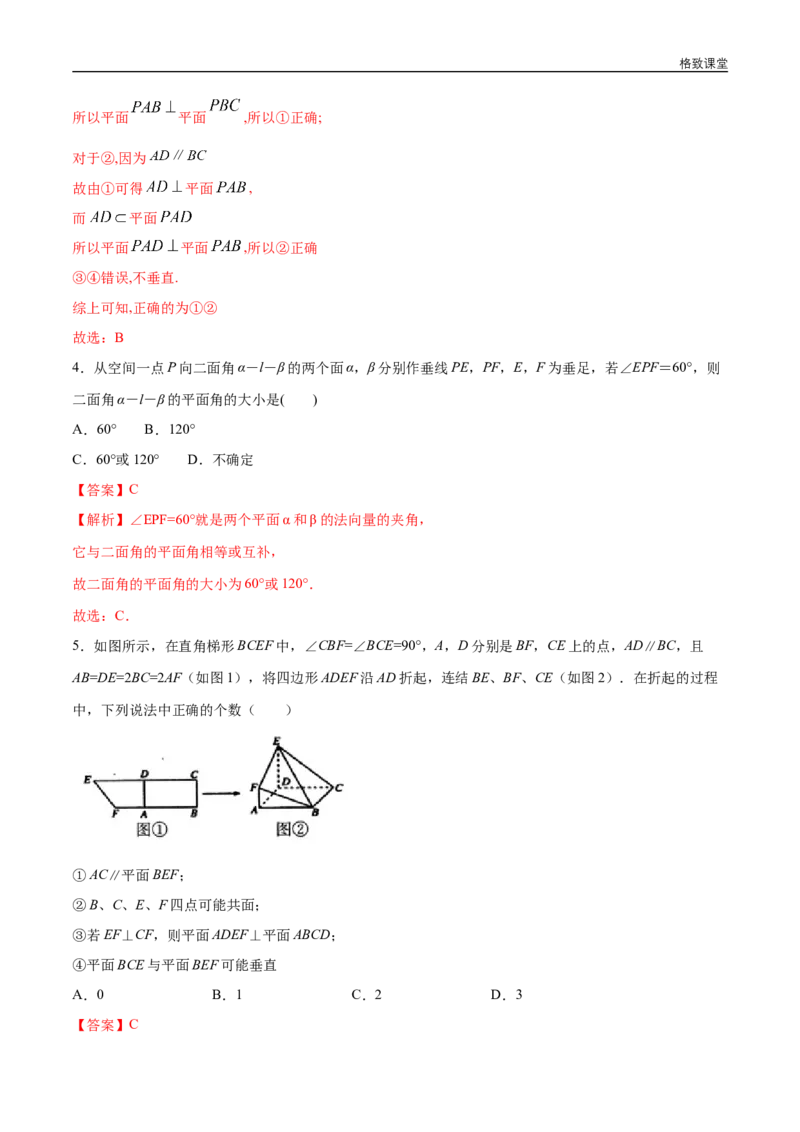
3. 垂直于正方形 所在平面,连接 , , , , ,则下列垂直关系正确的个
数是( )
①面 面 ②面 面
③面 面 ④面 面
A.1 B.2 C.3 D.4
【答案】B
【解析】证明:对于①,因为底面为正方形
所以
由题意可知 平面
所以 ,
而
所以 平面
又因为 平面格致课堂
所以平面 平面 ,所以①正确;
对于②,因为
故由①可得 平面 ,
而 平面
所以平面 平面 ,所以②正确
③④错误,不垂直.
综上可知,正确的为①②
故选:B
4.从空间一点P向二面角α-l-β的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则
二面角α-l-β的平面角的大小是( )
A.60° B.120°
C.60°或120° D.不确定
【答案】C
【解析】∠EPF=60°就是两个平面α和β的法向量的夹角,
它与二面角的平面角相等或互补,
故二面角的平面角的大小为60°或120°.
故选:C.
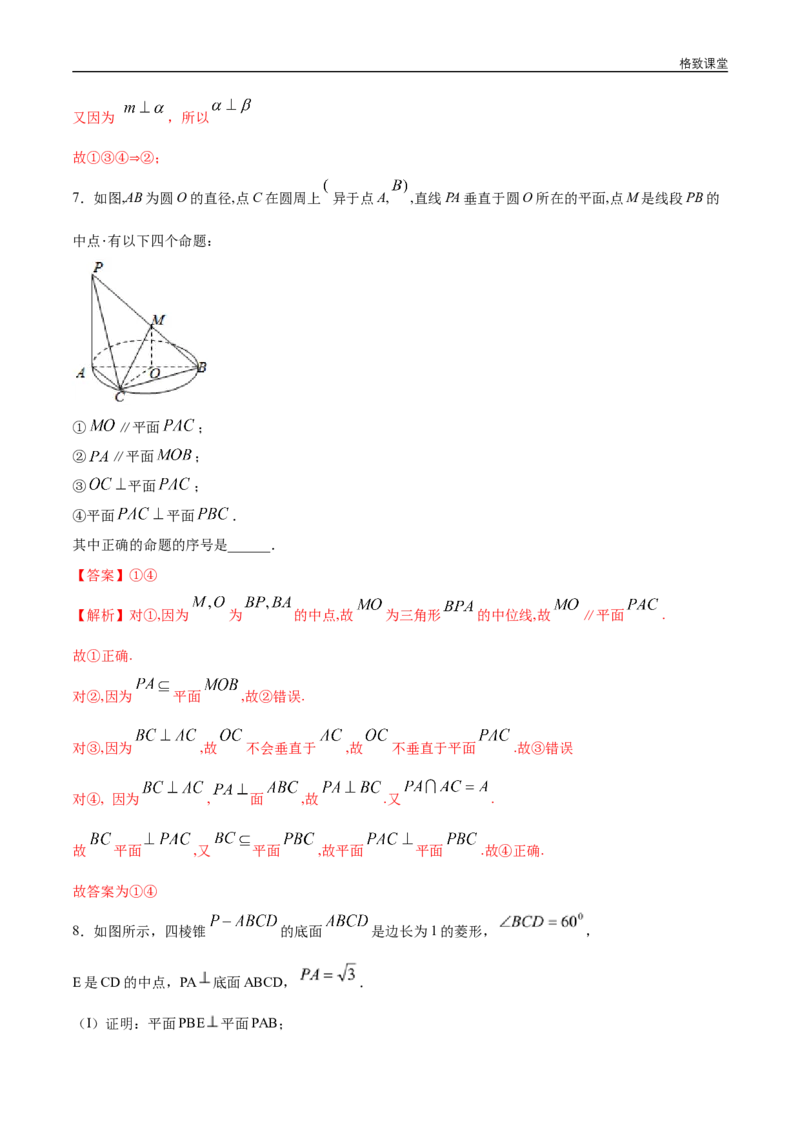
5.如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且
AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程
中,下列说法中正确的个数( )
①AC∥平面BEF;
②B、C、E、F四点可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④平面BCE与平面BEF可能垂直
A.0 B.1 C.2 D.3
【答案】C格致课堂
【解析】
对①,在图②中,连接 交于点 ,取 中点,连接MO,易证AOMF为平行四边形,即AC//
FM,所以AC//平面BEF,故①正确;
对②,如果B、C、E、F四点共面,则由BC//平面ADEF,可得BC//EF,又AD//BC,所以AD//EF,这样
四边形ADEF为平行四边形,与已知矛盾,故②不正确;
对③,在梯形ADEF中,由平面几何知识易得EF FD,又EF CF,∴EF 平面CDF,
即有CD EF,∴CD 平面ADEF,则平面ADEF 平面ABCD,故③正确;
对④,在图②中,延长AF至G,使得AF=FG,连接BG,EG,易得平面BCE 平面ABF,BCEG四点共
面.过F作FN BG于N,则FN 平面BCE,若平面BCE 平面BEF,
则过F作直线与平面BCE垂直,其垂足在BE上,矛盾,故④错误.
故选:C.
6.设α,β是空间内两个不同的平面,m,n是平面α及β外的两条不同直线.从“①m⊥n;②α⊥β;
③n⊥β;④m⊥α”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题:________(用
序号表示).
【答案】①③④⇒②
【解析】将①③④作为条件,
因为 所以 或 ,格致课堂
又因为 ,所以
故①③④⇒②;
7.如图,AB为圆O的直径,点C在圆周上 异于点A, ,直线PA垂直于圆O所在的平面,点M是线段PB的
中点 有以下四个命题:
① ∥平面 ;
② ∥平面 ;
③ 平面 ;
④平面 平面 .
其中正确的命题的序号是______.
【答案】①④
【解析】对①,因为 为 的中点,故 为三角形 的中位线,故 ∥平面 .
故①正确.
对②,因为 平面 ,故②错误.
对③,因为 ,故 不会垂直于 ,故 不垂直于平面 .故③错误
对④, 因为 , 面 ,故 .又 .
故 平面 ,又 平面 ,故平面 平面 .故④正确.
故答案为①④
8.如图所示,四棱锥 的底面 是边长为1的菱形, ,
E是CD的中点,PA 底面ABCD, .
(I)证明:平面PBE 平面PAB;格致课堂
(II)求二面角A—BE—P和的大小.
【答案】(I)同解析(II)二面角 的大小为
【解析】(I)如图所示, 连结 由 是菱形且 知,
BCD是等边三角形. 因为E是CD的中点,所以
△
又 所以
又因为PA 平面ABCD, 平面ABCD,
所以 而 因此 平面PAB.
又 平面PBE,所以平面PBE 平面PAB.
(II)由(I)知, 平面PAB, 平面PAB, 所以
又 所以 是二面角 的平面角.
在Rt PAB中, .
△
故二面角 的大小为
能力提升
9.在四面体 中,已知棱 的长为 ,其余各棱长都为1,则二面角 的平面角的
余弦值为( )格致课堂
A. B. C. D.
【答案】C
【解析】
由已知可得AD⊥DC
又由其余各棱长都为1得正三角形BCD,取CD得中点E,连BE,则BE⊥CD
在平面ADC中,过E作AD的平行线交AC于点F,则∠BEF为二面角A﹣CD﹣B的平面角
∵EF= (三角形ACD的中位线),BE= (正三角形BCD的高),BF= (等腰RT三角形ABC,
F是斜边中点)
∴cos∠BEF=
故选C.
10.如图所示,正方形 的边长为 ,已知 ,将△ABE沿 边折起,折起后 点在平
面 上的射影为 点,则翻折后的几何体中有如下描述:① 与 所成角的正切值为 ;
②AB//CE;③ ;④平面 平面 ,其中正确的命题序号为___________.格致课堂
【答案】③④
【解析】
作出折叠后的几何体直观图如图所示:
∵AB= a,BE=a,∴AE= a.
∴ .
∵BC∥DE,∴∠ABC是异面直线AB,DE所成的角,
在Rt ABC中, ,故①不正确;
△
连结BD,CE,则CE⊥BD,
又AD⊥平面BCDE,CE 平面BCDE,
∴CE⊥AD,又BD∩AD=⊂D,BD 平面ABD,AD 平面ABD,
∴CE⊥平面ABD,又AB 平面A⊂BD, ⊂
∴CE⊥AB.故②错误. ⊂
三棱锥B−ACE的体积 .
故③正确.
∵AD⊥平面BCDE,BC 平面BCDE,
∴BC⊥AD,又BC⊥CD⊂,
∴BC⊥平面ACD,∵BC 平面ABC,
∴平面ABC⊥平面ACD.⊂
故答案为③④.格致课堂
11.如图,在四棱锥 中,底面是边长为 的正方形,侧棱 ,求证:
(1) 平面 ;
(2)平面 平面 ;
(3)二面角 的平面角的大小.
【答案】(1)见解析;(2)见解析;(3)
【解析】(1) , .
.
同理可证 .
平面 .
(2)由(1)知 平面 , 平面 , .
∵四边形 是正方形, .
又 , 平面 .
又 平面 ,∴平面 平面 .格致课堂
(3)由(1)知 平面 , 平面 , .
又 , 平面 .
平面 , .
为二面角 的平面角.
在 中, .
∴二面角 的平面角的大小为45°.
素养达成
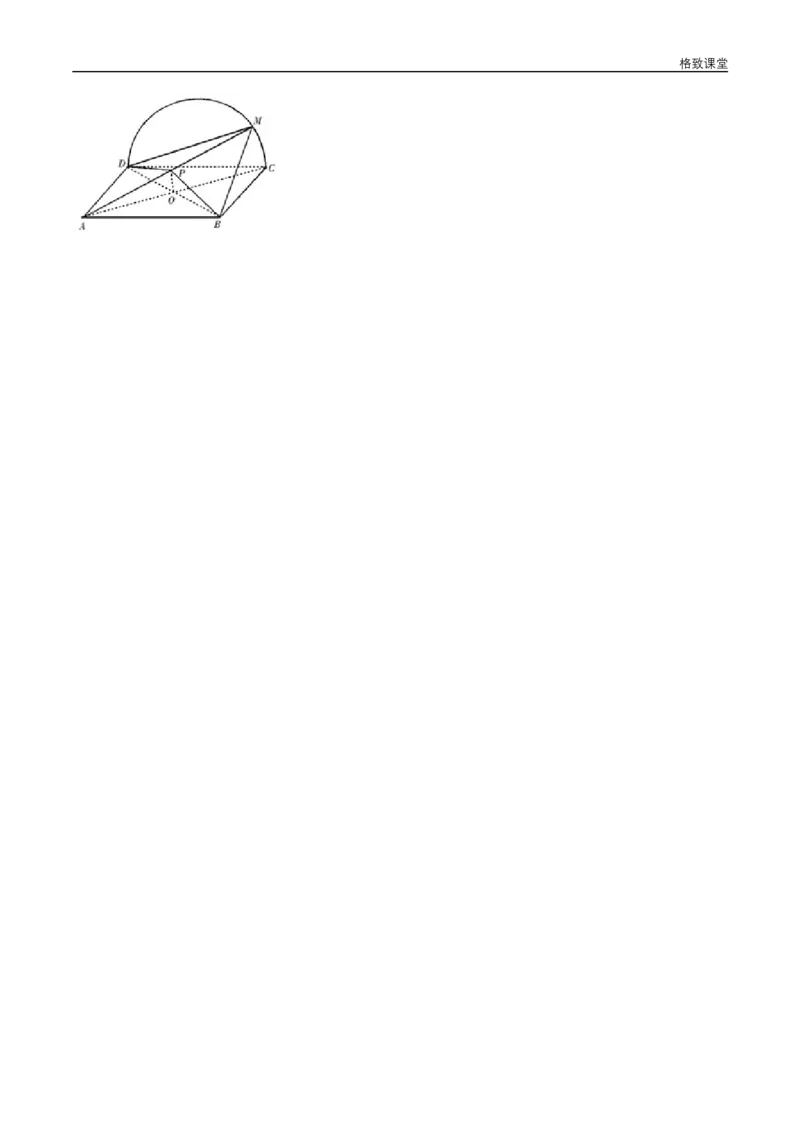
12.如图,矩形 所在平面与半圆弧CD所在平面垂直, 是CD上异于 , 的点.
(1)证明:平面 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ?说明理由.
【答案】(1)证明见解析.(2)存在,理由见解析.
【解析】(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC 平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为 上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM 平面AMD,故平面AMD⊥平面BMC.
(2)当P为AM的中点时,MC∥平面PBD.
证明如下:连结AC交BD于O.因为ABCD为矩形,所以O为AC中点.
连结OP,因为P为AM 中点,所以MC∥OP.
MC 平面PBD,OP 平面PBD,所以MC∥平面PBD.格致课堂