文档内容
新高考地区高 2024 届高二(上)第一次月考模拟一
数学试卷
注意事项:
1.答题前,考生务必将自己的姓名、准考证号、班级、学校在答题卡上填写清楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦
干净后,再选涂其他答案标号.在试卷上作答无效.
3.考试结束后,请将答题卡交回,试卷自行保存.满分150分,考试用时120分钟.
一、单选题:本题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项
是符合题目要求的.
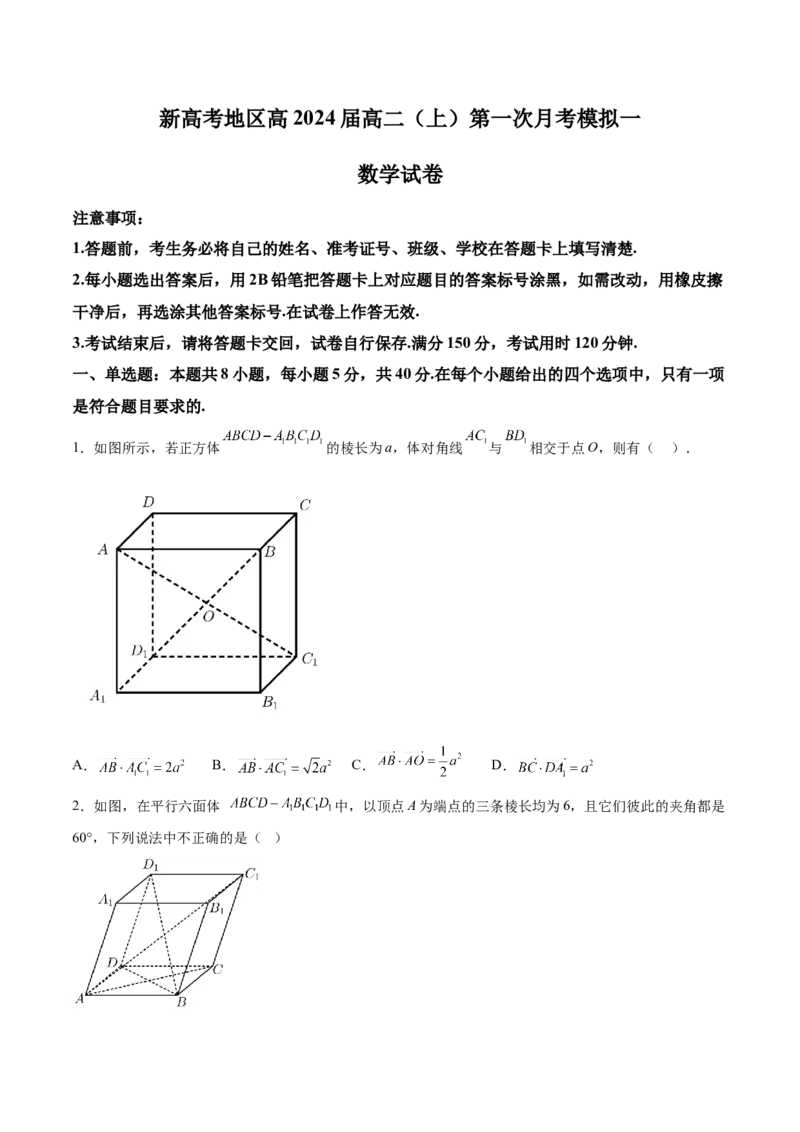
1.如图所示,若正方体 的棱长为a,体对角线 与 相交于点O,则有( ).
A. B. C. D.
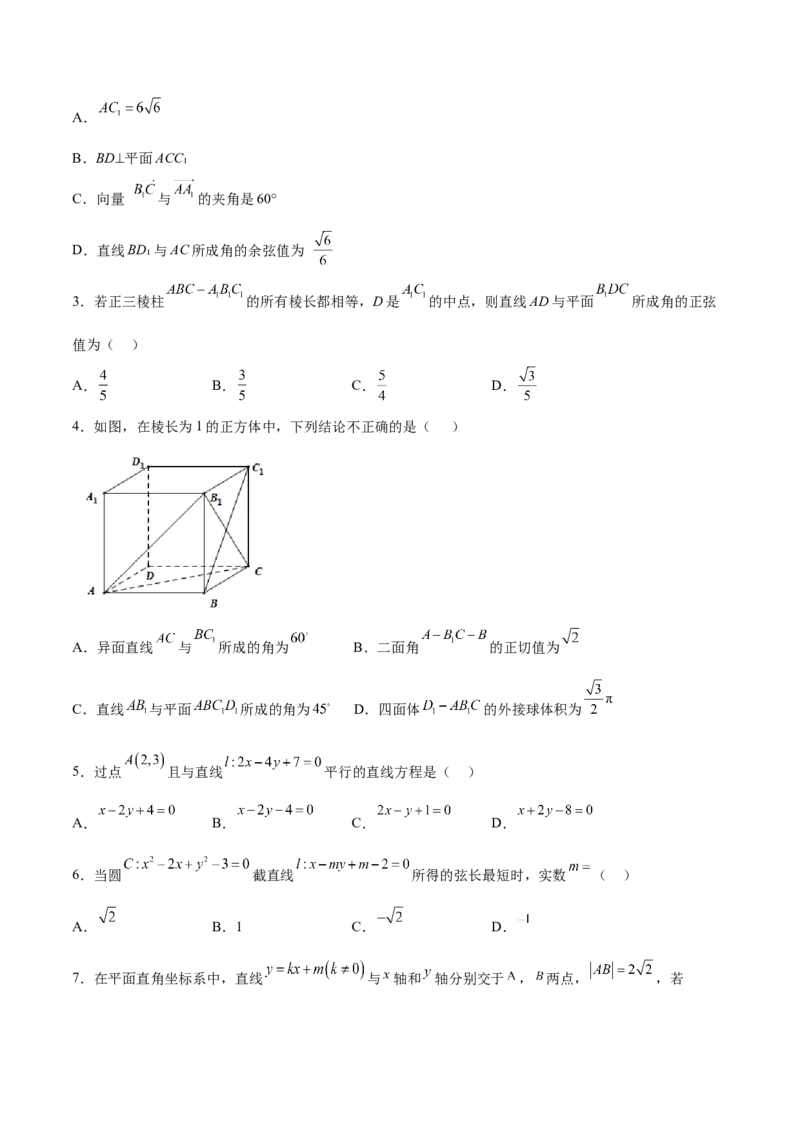
2.如图,在平行六面体 中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是
60°,下列说法中不正确的是( )A.
B.BD⊥平面ACC₁
C.向量 与 的夹角是60°
D.直线BD₁与AC所成角的余弦值为
3.若正三棱柱 的所有棱长都相等,D是 的中点,则直线AD与平面 所成角的正弦
值为( )
A. B. C. D.
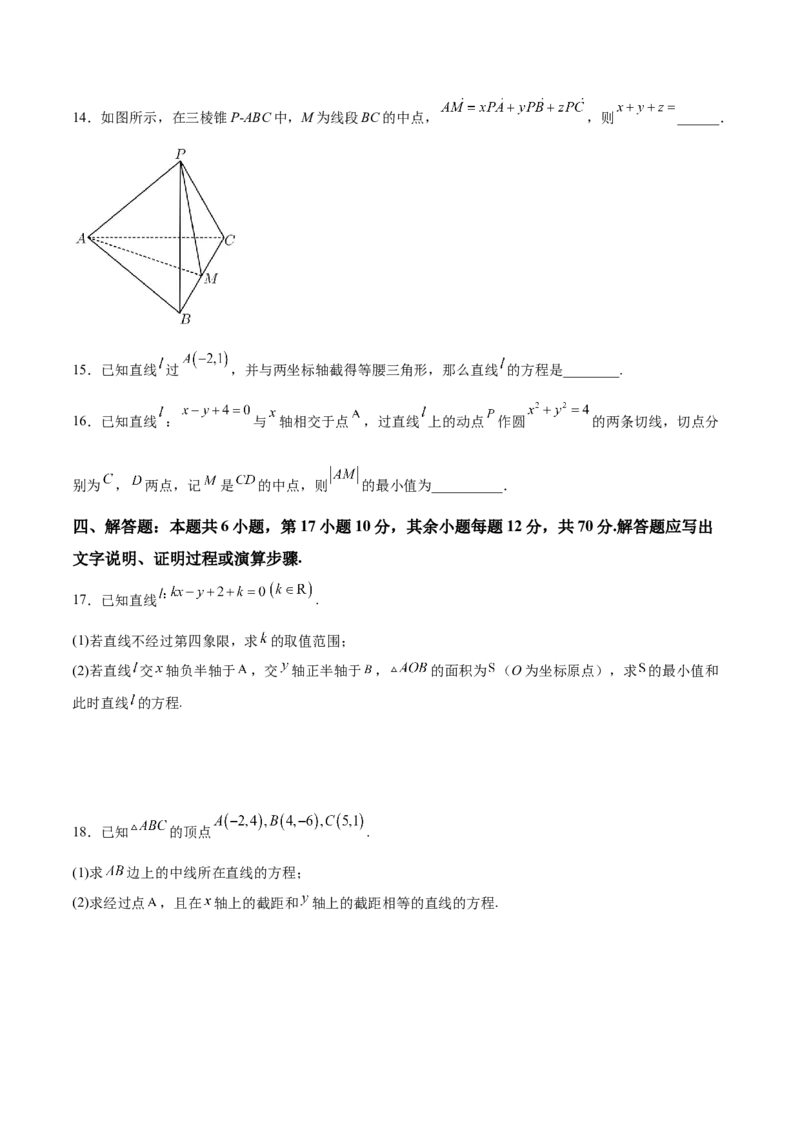
4.如图,在棱长为1的正方体中,下列结论不正确的是( )
A.异面直线 与 所成的角为 B.二面角 的正切值为
C.直线 与平面 所成的角为 D.四面体 的外接球体积为
5.过点 且与直线 平行的直线方程是( )
A. B. C. D.
6.当圆 截直线 所得的弦长最短时,实数 ( )
A. B.1 C. D.
7.在平面直角坐标系中,直线 与 轴和 轴分别交于 , 两点, ,若,则当 , 变化时,点 到点 的距离的最大值为( )
A. B. C. D.
8.设 ,过定点 的动直线 和过定点 的动直线 交于点 ,则
的最大值( )
A. B. C.3 D.6
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知空间三点 ,设 .则下列结论正确的是( )
A.若 ,且 ,则
B. 和 的夹角的余弦值
C.若 与 互相垂直,则k的值为2;
D.若 与z轴垂直,则 , 应满足
10.如图,已知 , 分别是正方体 的棱 和 的中点,则( )
A. 与 是异面直线B. 与 所成角的大小为
C. 与平面 所成角的余弦值为
D.二面角 的余弦值为
11.已知圆 ,直线 ,点 在直线 上运动,直线 分别于圆 切于
点 .则下列说法正确的是( )
A.四边形 的面积最小值为
B. 最短时,弦 长为
C. 最短时,弦 直线方程为
D.直线 过定点
12.已知直线 ,圆 ,则下列选项中正确的是
( )
A.圆心 的轨迹方程为
B. 时,直线 被圆截得的弦长的最小值为
C.若直线 被圆 截得的弦长为定值,则
D. 时,若直线 与圆相切,则
三、填空题:本题共4小题,每小题5分,共20分.
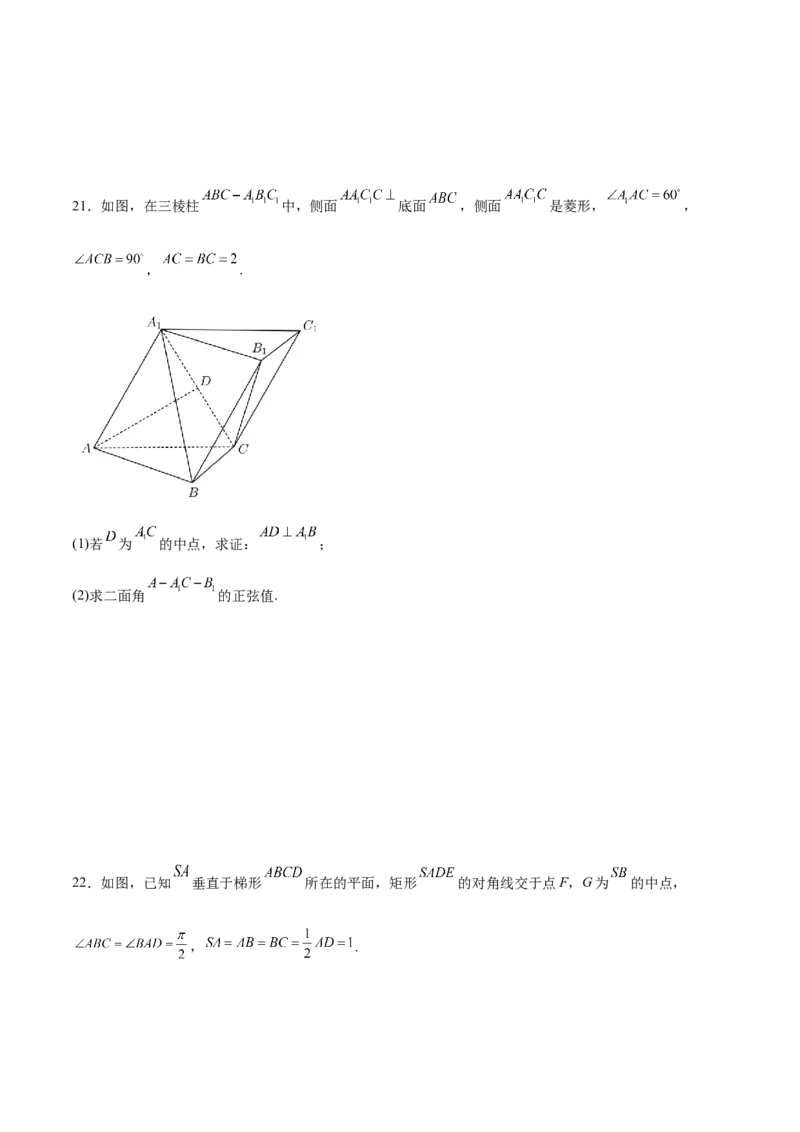
13.若三个向量 , , 共面,则实数m的值为______.14.如图所示,在三棱锥P-ABC中,M为线段BC的中点, ,则 ______.
15.已知直线 过 ,并与两坐标轴截得等腰三角形,那么直线 的方程是________.
16.已知直线 : 与 轴相交于点 ,过直线 上的动点 作圆 的两条切线,切点分
别为 , 两点,记 是 的中点,则 的最小值为__________.
四、解答题:本题共6小题,第17小题10分,其余小题每题12分,共70分.解答题应写出
文字说明、证明过程或演算步骤.
17.已知直线 .
(1)若直线不经过第四象限,求 的取值范围;
(2)若直线 交 轴负半轴于 ,交 轴正半轴于 , 的面积为 (O为坐标原点),求 的最小值和
此时直线 的方程.
18.已知 的顶点 .
(1)求 边上的中线所在直线的方程;
(2)求经过点 ,且在 轴上的截距和 轴上的截距相等的直线的方程.19.已知圆 的圆心在坐标原点,且过点 .
(1)求圆 的方程;
(2)已知点 是圆 上的动点,试求点 到直线 的距离的最小值;
(3)若直线 与圆 相切,且 与 轴的正半轴分别相交于 两点,求 的面积最小时直线 的方程.
20.已知圆 过点 ,且与直线 相切于点 .
(1)求圆 的方程;
(2)过点 的直线 与圆 交于 两点,若 为直角三角形,求直线 的方程;
(3)在直线 上是否存在一点 ,过点 向圆 引两切线,切点为 ,使 为正三角形,若
存在,求出点 的坐标,若不存在,说明理由.21.如图,在三棱柱 中,侧面 底面 ,侧面 是菱形, ,
, .
(1)若 为 的中点,求证: ;
(2)求二面角 的正弦值.
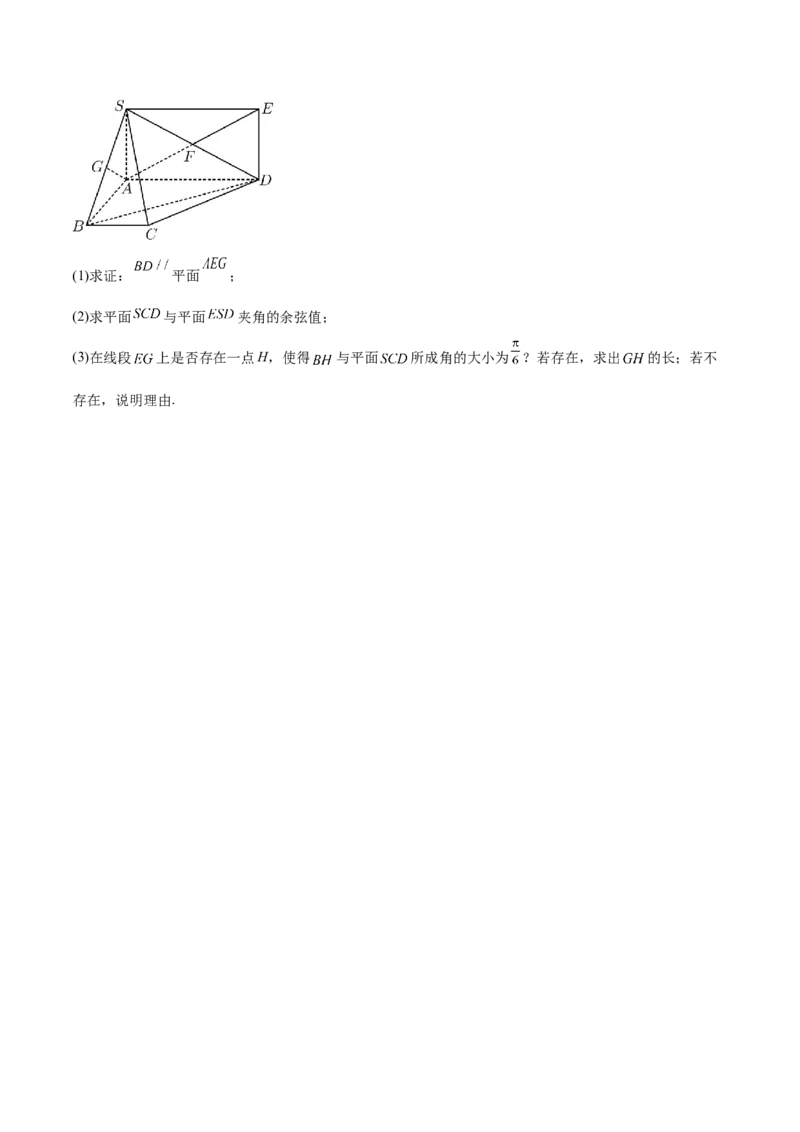
22.如图,已知 垂直于梯形 所在的平面,矩形 的对角线交于点F,G为 的中点,
, .(1)求证: 平面 ;
(2)求平面 与平面 夹角的余弦值;
(3)在线段 上是否存在一点H,使得 与平面 所成角的大小为 ?若存在,求出 的长;若不
存在,说明理由.