文档内容
期中测试卷
(考试范围:人教A版2019选择性必修第三册)
姓名: 班级:
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符
合题目要求的。
1.A、B、C、D四人并排站成一排,如果A与B相邻,那么不同的排法种数是( )。
A、24种
B、12种
48
C、 种
23
D、 种
2.某人民医院召开抗疫总结表彰大会,有7名先进个人受到表彰,其中有一对夫妻。现要选3人上台报告
事迹,要求夫妻两人中至少有1人报告,若夫妻同时被选,则两人的报告顺序需要相邻,这样不同的报告
方案共有( )。
80
A、 种
120
B、 种
130
C、 种
140
D、 种
3.从4件合格品和2件次品共6件产品中任意抽取2件检查,抽取的2件中至少有1件是次品的概率是
( )。
2
5
A、
3
5
B、
8
15
C、
2
3
D、
2
(x2 +m)⋅(x− ) 6
x x4 30
4.若 的展开式中 的系数为 ,则m的值为( )。
15
−
2
A、
5
−
2
B、5
2
C、
15
2
D、
5.我国古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水
克火,火克金。”将这五种不同属性的物质任意排成一排,设事件A表示“排列中属性相克的两种物质均
不相邻”,则事件A发生的概率为( )。
1
24
A、
1
12
B、
1
6
C、
5
12
D、
(2−x) 7 =a +a⋅(1+x)+a⋅(1+x) 2 +¿⋅¿+a⋅(1+x) 7 a +a +a +¿⋅¿+a =
6.记 0 1 2 7 ,则 0 1 2 6 ( )。
A、−1
B、2
129
C、
256
D、
7.
2019
年末,武汉出现新型冠状病毒肺炎(
COVID−19
)疫情,并快速席卷我国其他地区,传播速度很
快。因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大,
武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊
的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等
“四类”人员,强化网格化管理,不落一户、不漏一人。在排查期间,一户6口之家被确认为“与确诊患
者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,
则该家庭为“感染高危户”。设该家庭每个成员检测呈阳性的概率均为p( 01)=0.68 P(2≤X<3)=0.18
D、若随机变量 , ,则
1 1
a∈(0, ) (0, )
11.设 3 ,随机变量X的分布列如表所示,随机变量Y=3X+2,则当a在 3 上增大时,下列
E(Y) D(Y)
关于 、 的表述正确的是( )。
X −2 −1 0
P 2b b−a a
E(Y)
A、 增大
E(Y)
B、 先减小后增大
D(Y)
C、 先增大后减小
D(Y)
D、 增大12.骰子通常作为桌上游戏的小道具。最常见的骰子是六面骰,它是一个质地均匀的正方体,六个面上分
别写有数字1、2、3、4、5、6。现有一款闯关游戏,共有4关,规则如下:在第n关要抛掷六面骰n
次,每次观察向上面的点数并做记录,如果这n次抛掷所出现的点数之和大于
2n +n
,则算闯过第n关,
n=1、2、3、4,假定每次闯关互不影响,则( )。
7
A、直接挑战第2关并过关的概率为 12
5
24
B、连续挑战前两关并过关的概率为
C、若直接挑战第3关,设A= “三个点数之和等于 15 ”, B= “至少出现一个5点”,则
1
P(A|B)=
13
35
D、若直接挑战第4关,则过关的概率是 1296
三、填空题:本题共4小题,每小题5分,共20分。
1
X~B(n, )
13.设随机变量 4 ,Y=2X+1,若 E(Y)=4 ,则n= 。
14.某班举行了由甲、乙、丙、丁、戊5名学生参加的“弘扬中华文化”的演讲比赛,决出第1名到第5名
的名次。甲、乙两名参赛者去询问成绩,回答者对甲说,“很遗憾,你和乙都没有得到冠军”;对乙说,
“你当然不会是最差的”从这个回答分析,5人的名次排列情况可能有 种。(请用具体数字作
答)
15.已知 (x−1) 3 (x+a) 2 (a∈Z)的展开式中x的系数等于8,则展开式中 x3 的系数等于 。
16.为了抗击新冠肺炎变种奥密克戎引起的疫情,现从四川省成都市的A医院 150 人和B医院 100 人中,
按分层抽样的方法,选出5人加入“援沪医疗队”,现拟再从此5人中选出两人作为联络人,则这两名联
络人中B医院至少有一人的概率是 ;设两名联络人中B医院的人数为X,则X 的期望为
。(本小题第一个空2分,第二个空3分)
四、解答题:本题共6小题,共70分。应写出文字说明、证明过程或演算步骤。
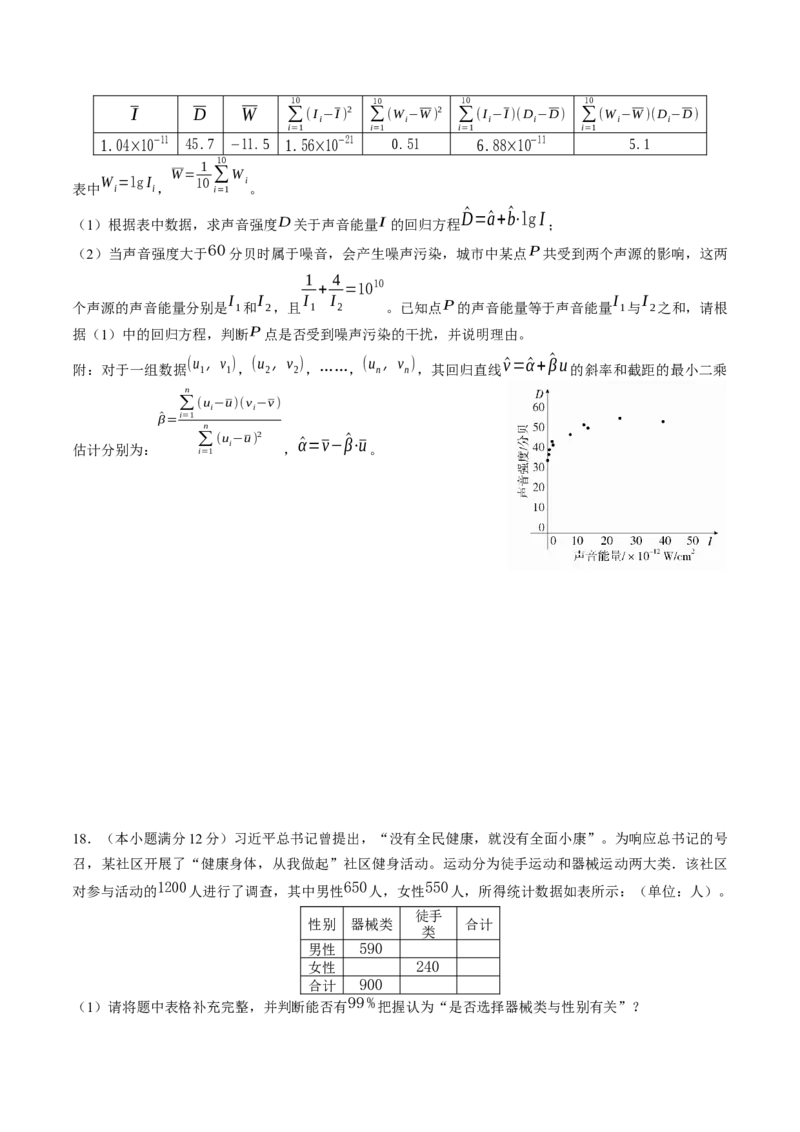
17.(本小题满分10分)噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解强度D
(单位:分贝)与声音能量I (单位:
W/cm2
)之间的关系,将测量得到的声音强度
D
i和声音能量
I
i(
i=1、2、…、 10 )数据作了初步处理,得到下面的散点图及一些统计量的值。10 10 10 10
I D W ∑(I −I)2 ∑(W −W)2 ∑(I −I)(D−D) ∑(W −W)(D−D)
i i i i i i
i=1 i=1 i=1 i=1
1.04×10−11 45.7 −11.5 1.56×10−21 0.51 6.88×10−11 5.1
10
1
W= ∑W
W =lgI 10 i
表中 i i, i=1 。
(1)根据表中数据,求声音强度D关于声音能量I 的回归方程
D^ =a^+b^ ⋅lgI
;
(2)当声音强度大于 60 分贝时属于噪音,会产生噪声污染,城市中某点P共受到两个声源的影响,这两
1 4
+
=1010
I I I I I I
个声源的声音能量分别是 1和 2,且 1 2 。已知点P的声音能量等于声音能量 1与 2之和,请根
据(1)中的回归方程,判断P点是否受到噪声污染的干扰,并说明理由。
(u ,v ) (u ,v ) (u ,v ) ν^=α^+β^ u
附:对于一组数据 1 1 , 2 2 ,……, n n ,其回归直线 的斜率和截距的最小二乘
n
∑(u−u)(v−v)
i i
β^=i=1
n
估计分别为: ∑(u i −u)2 , α^=v−β^ ⋅u 。
i=1
18.(本小题满分12分)习近平总书记曾提出,“没有全民健康,就没有全面小康”。为响应总书记的号
召,某社区开展了“健康身体,从我做起”社区健身活动。运动分为徒手运动和器械运动两大类.该社区
1200 650 550
对参与活动的 人进行了调查,其中男性 人,女性 人,所得统计数据如表所示:(单位:人)。
徒手
性别 器械类 合计
类
男性 590
女性 240
合计 900
99%
(1)请将题中表格补充完整,并判断能否有 把握认为“是否选择器械类与性别有关”?(2)为了检验活动效果,该社区组织了一次竞赛活动。竞赛包括三个项目,一个是器械类,两个是徒手
4
5
类,规定参与者必需三个项目都参加。据以往经验,参赛者通过器械类竞赛的概率是 ,通过徒手类竞赛
3
4 ξ
的概率都是 ,且各项目是否通过相互独立。用 表示某居民在这次竞赛中通过的项目个数,求随机变量
ξ
的分布列和数学期望。
(参考数据:
12302 =1518900
,
65×65×9=32175
,
1518900÷32175≈47
)
n(ad−bc) 2
K2
=
(a+b)(a+c)(c+d)(b+d)
附: 。
P(K2 >k) 0.050 0.025 0.010 0.005 0.001
k 3.841 5.024 6.635 7.879 10.828
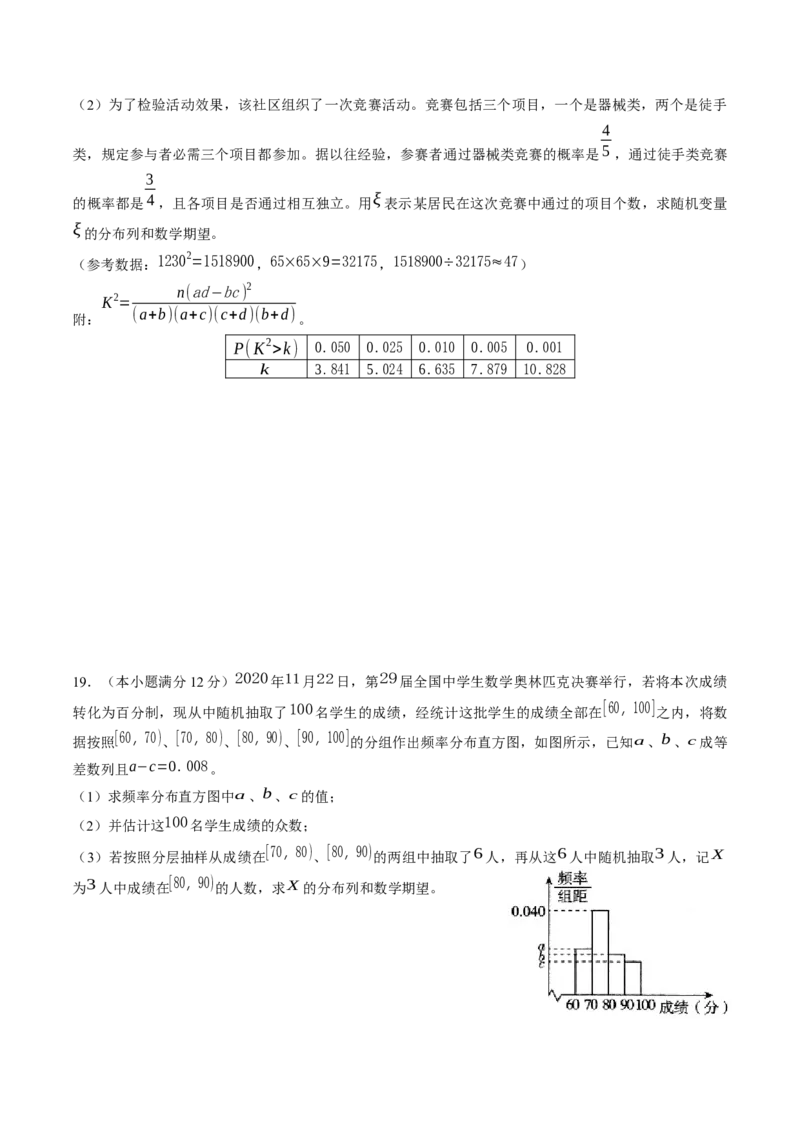
19.(本小题满分12分) 2020 年11月22日,第 29 届全国中学生数学奥林匹克决赛举行,若将本次成绩
转化为百分制,现从中随机抽取了
100 名学生的成绩,经统计这批学生的成绩全部在[60,100]之内,将数
据按照[60,70)、[70,80)、[80,90)、 [90,100] 的分组作出频率分布直方图,如图所示,已知a、b、c成等
差数列且a−c=0.008
。
(1)求频率分布直方图中a、b、c的值;
100
(2)并估计这 名学生成绩的众数;
(3)若按照分层抽样从成绩在[70,80)、[80,90)的两组中抽取了6人,再从这6人中随机抽取3人,记X
为3人中成绩在[80,90)的人数,求X的分布列和数学期望。20.(本小题满分12分)北京时间 2021 年11月7日凌晨1点。来自中国赛区的 EDG 战队,捧起了英雄联
盟S11
全球总决赛的冠军奖杯,据统计,仅在
bilibili 平台,S11 总决赛的直播就有3.5亿人观看,电子竞
技作为正式体育竞赛项目已经引起越来越多的年轻人关注,已知该项赛事的季后赛后半段有四支战队参加,
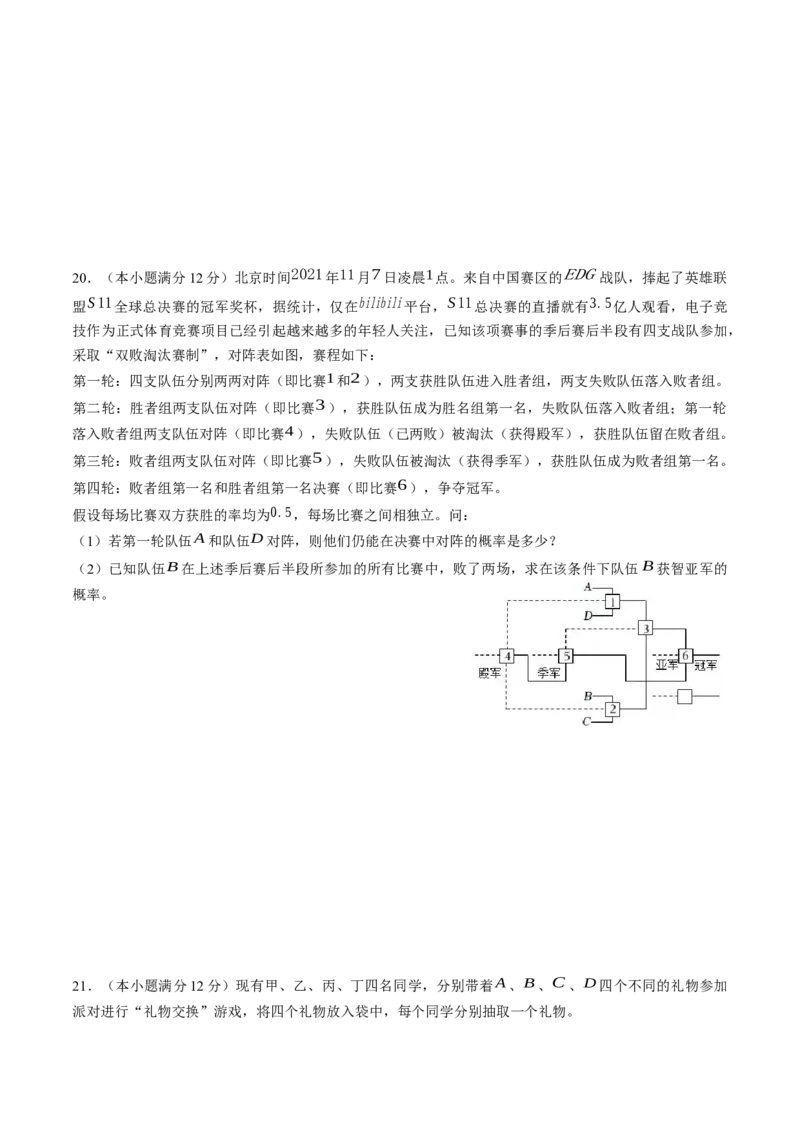
采取“双败淘汰赛制”,对阵表如图,赛程如下:
第一轮:四支队伍分别两两对阵(即比赛1和2),两支获胜队伍进入胜者组,两支失败队伍落入败者组。
第二轮:胜者组两支队伍对阵(即比赛3),获胜队伍成为胜名组第一名,失败队伍落入败者组;第一轮
落入败者组两支队伍对阵(即比赛4),失败队伍(已两败)被淘汰(获得殿军),获胜队伍留在败者组。
第三轮:败者组两支队伍对阵(即比赛5),失败队伍被淘汰(获得季军),获胜队伍成为败者组第一名。
第四轮:败者组第一名和胜者组第一名决赛(即比赛6),争夺冠军。
假设每场比赛双方获胜的率均为0.5,每场比赛之间相独立。问:
(1)若第一轮队伍A和队伍D对阵,则他们仍能在决赛中对阵的概率是多少?
(2)已知队伍B在上述季后赛后半段所参加的所有比赛中,败了两场,求在该条件下队伍B获智亚军的
概率。
21.(本小题满分12分)现有甲、乙、丙、丁四名同学,分别带着A、B、C、D四个不同的礼物参加
派对进行“礼物交换”游戏,将四个礼物放入袋中,每个同学分别抽取一个礼物。(1)求四位同学都没有拿到自己所带的礼物的概率;
(2)记X 为未拿到自己所带的礼物的同学的人数,求X的分布列和数学期望。
22.(本小题满分12分)条件概率和条件期望是现代概率体系中的重要概念,近年来,随着人们对随机现
象的不断观察和研究,条件概率和条件期望已经被广泛的利用到日常生产生活中。我们可以进行定义:设
X、 Y 是 离 散 型 随 机 变 量 , 则 X 在 给 定 事 件 Y=y 条 件 下 的 期 望 为 :
n
E(X|Y=y)=∑x⋅P(X=x|Y=y)=
i i
i=1
n P(X=x,Y=y)
∑x⋅ i
i=1 i P(Y=y) ,其中 {x 1 ,x 2 ,⋅¿⋅,x n } 为X的所有可能取值集合。 P(X=x,Y=y)表示事件“
X=x”与事件“ Y=y ”都发生的概率。
某射击手进行射击训练,每次射击击中目标的概率均为p( 0