新疆喀什市2024-2025学年高一下学期期中考试数学Word版含答案_2024-2025高一（7-7月题库）_2025年05月试卷_0530新疆喀什市2024-2025学年高一下学期期中考试

喀什市 2024-2025 学年第二学期期中质量监测试卷 高一 数学 注意事项： 1.本试卷共150分，考试用时120分钟。 2.本试卷为问答分离式试卷，其中问卷4页。所有答案一律写在答题卷上，在问卷上答题无效。. 一、单选题（共8小题，每小题5分，共40分） 1．已知向量 ，则 （ ） 10,5 1,8 5,10 7,6 A． B． C． D． z 13i z 3i z z 2．已知复数 1 ， 2 ，则 1 2在复平面内对应的点所在的象限为（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限  3.若 a 3 ， b 4 ，a ，b  的夹角为135，则a  b  等于（ ） 6 2 3 2 2 2 A． B． C． D． 4．各棱长均为a的三棱锥的表面积为 4 3a2 3 3a2 2 3a2 3a2 A. B. C. D. 4 6 b 5.在 中，内角A，B，C所对的边分别为a，b，c，且a 4， 3 ，A60，则 B （ ） 30 30 150 45 45 135 A. B. 或 C. D. 或 6．如图，在 中， ，点 是 的中点．设 ， ，则 （ ） A． B． 2 a 1 b  3 6 C． 1 a 2 b  D． 1 a 2 b  6 3 6 3 7.已知平面向量a,b  ，若 a 3,ab   13,ab  6，则向量 a与向量 b 的夹角为（ ）π π 2π 5π A． B． C． D． 6 3 3 6 8.桂林日月塔又称金塔银塔､情侣塔，日塔别名叫金塔，月塔别名叫银塔，所以也有 金银塔之称.如图1，这是金银塔中的金塔，某数学兴趣小组成员为测量该塔的高度， O A,B A P 在塔底 的同一水平面上的 两点处进行测量，如图2.已知在 处测得塔顶 的仰 B P AB25 AOB30 OP 角为60°，在 处测得塔顶 的仰角为45°， 米， ，则该塔的高度 （ ） 25 2 25 6 A． 米 B． 米 25 3 C．50米 D． 米 二、多选题（共4小题，每小题5分，共20分，在每小题给出的选项中有多项符合题目要求，全部选对 的得5分，部分选对的得2分，有选错的得0分）   e,e 9．已知 1 2是平面内的一组基底，则下列向量中能作为一组基底的是（ ）         e e e e 3e e 6e 4e A． 1 2和 1 2 B． 1 2 和 1 2        e e e e e e e C． 1 2和 2 1 D． 2和 2 1   a x,3 b5,2 10． 已知向量 ， ，则下列结论正确的是( ) 15 6   x   x A.若a//b，则 2 B.若a b，则 5  a 5   C.若 ，则x4 D.若x3，则ab21 13i 11.已知复数z （ 是虚数单位），则下列结论正确的是（ ） 1i i z 2i zz  5 A．复数 的虚部等于 B． zz2 a za a1 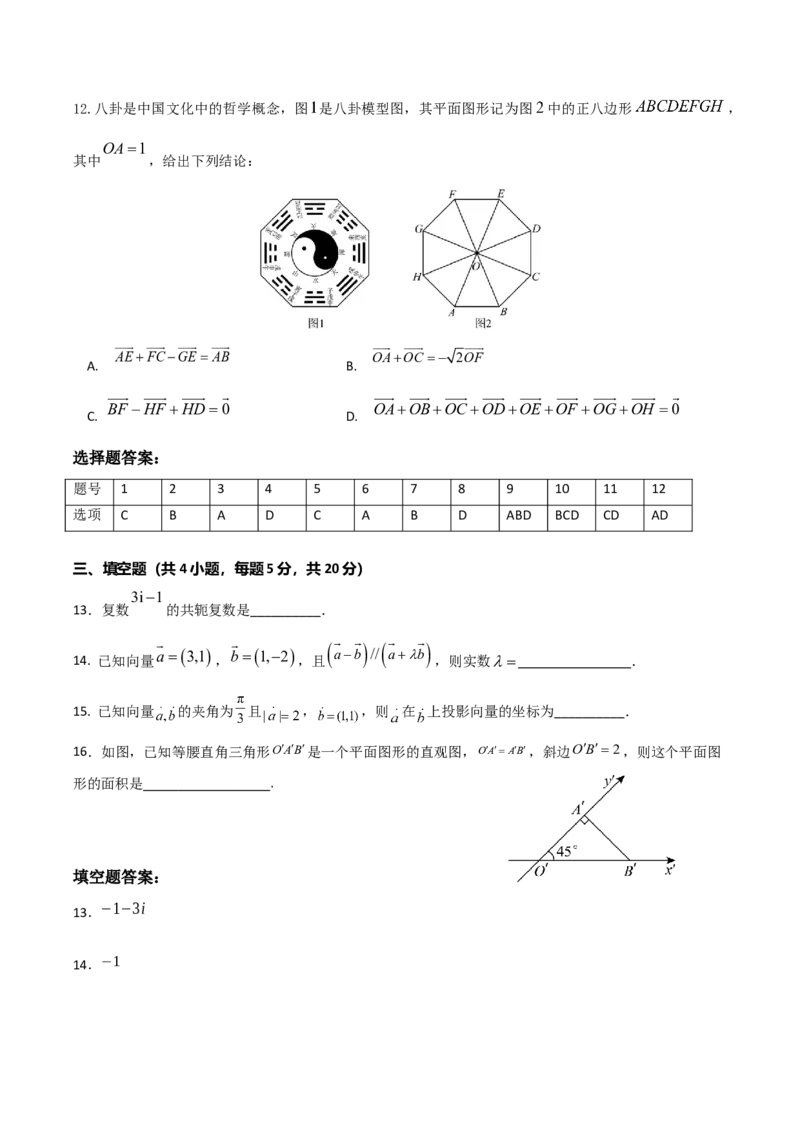C． D．若 是实数， 是纯虚数，则12.八卦是中国文化中的哲学概念，图 是八卦模型图，其平面图形记为图 中的正八边形 ， OA1 其中 ，给出下列结论：        AEFCGE  AB OAOC  2OF A. B.              BF HF HD0 OAOBOCODOEOF OGOH 0 C. D. 选择题答案： 题号 1 2 3 4 5 6 7 8 9 10 11 12 选项 C B A D C A B D ABD BCD CD AD 三、填空题（共4小题，每题5分，共20分） 3i1 13．复数 的共轭复数是__________．       a 3,1 b1,2 ab // ab 14. 已知向量 ， ，且 ，则实数 ． 15. 已知向量 的夹角为 且 ， ，则 在 上投影向量的坐标为__________． 16．如图，已知等腰直角三角形OAB是一个平面图形的直观图，OAAB，斜边OB2，则这个平面图 形的面积是 . 填空题答案： 13．−1−3i 14．−1(√2 √2) ， 2 2 15． 2√2 16． 四、解答题（共6小题，共70分） 17．（10分）计算： (1)(−3)×4⃗a； (2) ； 3(⃗a+⃗b)−2(⃗a−⃗b)−⃗a (3) ； (4) ； (5)⃗NQ+⃗QP+⃗MN−⃗MP. 【解答过程】（1） → →； (−3)×4a=−12a （2） ； 3(⃗a+⃗b)−2(⃗a−⃗b)−⃗a=3⃗a+3⃗b−2⃗a+2⃗b−⃗a=5⃗b (3) -2-11i (4) i (5) （5） ⃗NQ+⃗QP+⃗MN−⃗MP=⃗NP+(⃗MN−⃗MP) =⃗NP+⃗PN=0⃗. 18．（12分）已知复数 ， （i为虚数单位）． |¯z| （1）当 时，求 ； （2）若z为纯虚数，求m的值； （3）若复数z在复平面内对应的点位于第三象限，求m的取值范围． √5 【答案】（1） （2） （3） （1）¯z=2+i,∴|¯z|=√5 当 时， ，故 （2） { 2 m −m=0¿¿¿¿ m=0或m=1 ，解得 （3） 若复数z在复平面内对应的点 位于第三象限， 则 ，解得 ， 所以m的取值范围为 19.（12分）已知向量 与 的夹角为 ， ， . （I）若 ，求实数k的值； （II）是否存在实数k，使得 ？说明理由. （1） ;（2） （Ⅰ）∵向量 与 的夹角为 ， 又 且 ， （Ⅱ）若 ，则 ，使 又向量 与 不共线解得： 存在实数 时，有 ． 20．在 中， ， ， ． （1）求 的面积； （2）求 及 的值． 【答案】（1）22 （2） ， （1） 因为在 中， ， ， 结合平方关系 ，可知 ， 从而由三角形面积公式，可知 的面积为 . （2） 因 在 中， ， ， ， 为 所以由余弦定理有 ， 又 ，所以解得 ， 由（1）可知 ， 所以由正弦定理有 ，即 ，解得 . 21.（12分）如图，已知在正四棱锥SABCD中，SA5，AB6. (1)求四棱锥SABCD的表面积； (2)求四棱锥SABCD的体积. 答案：(1)84 (2) 解析：（1）连接 相交于 ，连接 过点 作 于点 ，连接 ，则 是斜高， 在直角三角形 中， ， 在直角三角形 中， ， ， ． 所以正四棱锥 的表面积为84． （2） ， 所以正四棱锥 的体积为 ； 22.（12分）在△ 中， ， ． （1）求 的大小；（2）在下列三个条件中选择一个作为已知，使 存在且唯一确定，并求出 边上的中线的长度． 条件①：△ 的周长为 ； 条件②：△ 的面积为 ． 注：如果选择多个符合要求的条件分别解答，按第一个解答计分． 【答案】（1） （2）选择条件②或③， （1） 在 中，因为 ，又 ，所以 ． 因为 ，所以 ． 因为 ，所以 ． （2） 选择条件②：因为 中， ， ， ， 所以 ，即 为等腰三角形，其中 ． 因为 ，所以 ． 所以 ． 设点 为线段 的中点，在 中， ． 因为 中，， 所以 ，即 边上的中线的长度为 ． 选择条件③：因为 中， ， ， ， 所以 ，即 为等腰三角形，其中 ． 因为 的面积为 ，即 ， 所以 ． 设点 为线段 的中点，在 中， ． 因为 中， ，