数学答案-河北保定一中2024-2025学年高一（第八届贯通班）上学期开学考试_2024-2025高一（7-7月题库）_2024年9月试卷

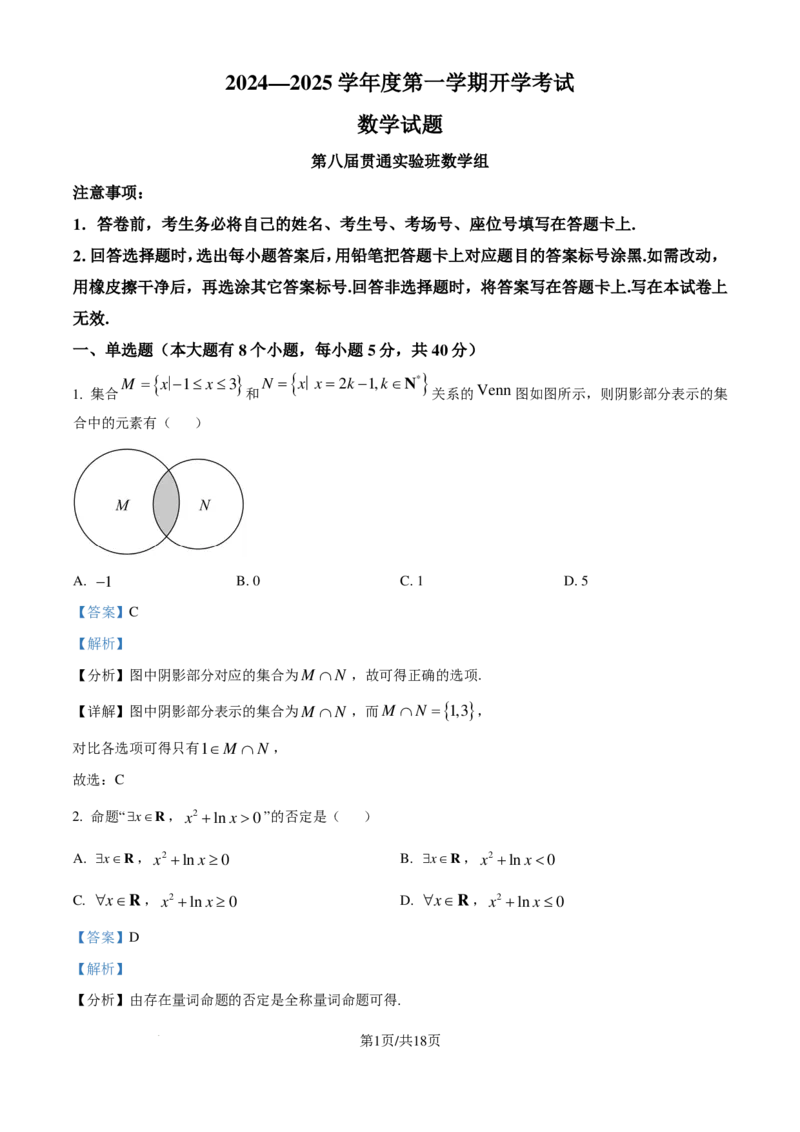
2024—2025 学年度第一学期开学考试 数学试题 第八届贯通实验班数学组 注意事项： 1．答卷前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上. 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动， 用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上 无效. 一、单选题（本大题有 8个小题，每小题 5分，共 40分） M ={ x∣−1≤ x≤3 } N = { x∣x=2k−1,k∈N* } 1. 集合 和 关系的Venn图如图所示，则阴影部分表示的集 合中的元素有（ ） A. −1 B. 0 C. 1 D. 5 【答案】C 【解析】 【分析】图中阴影部分对应的集合为M ∩N ，故可得正确的选项. 【详解】图中阴影部分表示的集合为M ∩N ，而M ∩N ={ 1,3 } ， 对比各选项可得只有1∈M ∩N ， 故选：C 2. 命题“∃x∈R，x2 +lnx>0”的否定是（ ） A. ∃x∈R，x2 +lnx≥0 B. ∃x∈R，x2 +lnx<0 C. ∀x∈R，x2 +lnx≥0 D. ∀x∈R，x2 +lnx≤0 【答案】D 【解析】 【分析】由存在量词命题的否定是全称量词命题可得. 第1页/共18页 学科网（北京）股份有限公司【详解】命题“∃x∈R，x2 +lnx>0”的否定是“∀x∈R，x2 +lnx≤0”. 故选：D. 3. “不积跬步，无以至千里，不积小流，无以成江海.”此句话是出自荷子的《劝学》，由此推断，其中最后 一句“积小流”是“成江海”的（ ） A. 充分条件 B. 必要条件 C. 充要条件 D. 既不充分也不必要条件 【答案】B 【解析】 【分析】利用充分条件、必要条件的定义分析判断即得. 【详解】依题意，不积累一步半步的行程，就没有办法达到千里之远； 不积累细小的流水，就没有办法汇成江河大海，等价于“汇成江河大海，则积累细小的流水”， 所以“积小流”是“成江海”的的必要条件. 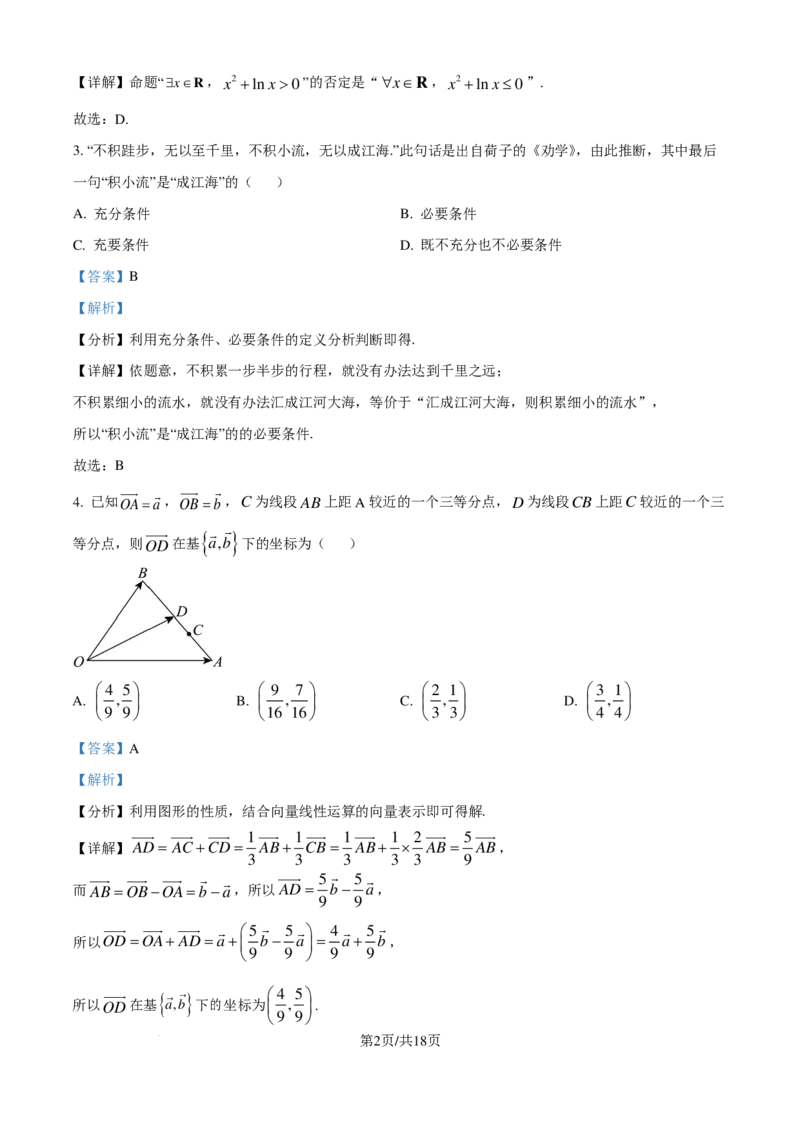故选：B     4. 已知OA=a，OB=b，C为线段AB上距A较近的一个三等分点，D为线段CB上距C较近的一个三  {  } 等分点，则OD在基 a,b 下的坐标为（ ） 4 5  9 7  2 1 3 1 A.  ,  B.  ,  C.  ,  D.  ,  9 9 16 16 3 3 4 4 【答案】A 【解析】 【分析】利用图形的性质，结合向量线性运算的向量表示即可得解.         1 1 1 1 2 5 【详解】AD= AC+CD= AB+ CB= AB+ × AB= AB， 3 3 3 3 3 9       5  5  而AB=OB−OA=b −a，所以AD= b − a， 9 9     5  5  4  5  所以OD=OA+ AD=a+  b − a = a+ b， 9 9  9 9  {  } 4 5 所以OD在基 a,b 下的坐标为 , . 9 9 第2页/共18页 学科网（北京）股份有限公司故选：A.  π 1 5. 已知α∈( 0,π ) ，且cos α+  = ，则cos2α=（ ）  4 3 4 2 4 2 7 7 A. B. ± C. D. ± 9 9 9 9 【答案】A 【解析】 【分析】利用二倍角公式结合角的余弦值确定角的范围计算即可.  π 1 π π π 【详解】因为α∈( 0,π ) ，cos α+  = >0，所以α+ ∈  , ，  4 3 4 4 2  π  π 2 2 则sin α+  = 1−cos2  α+  = ，  4  4 3   π π  π  π  π 4 2 则cos2α=cos2 α+  −  =sin2 α+  =2sin α+  ⋅cos α+  = . 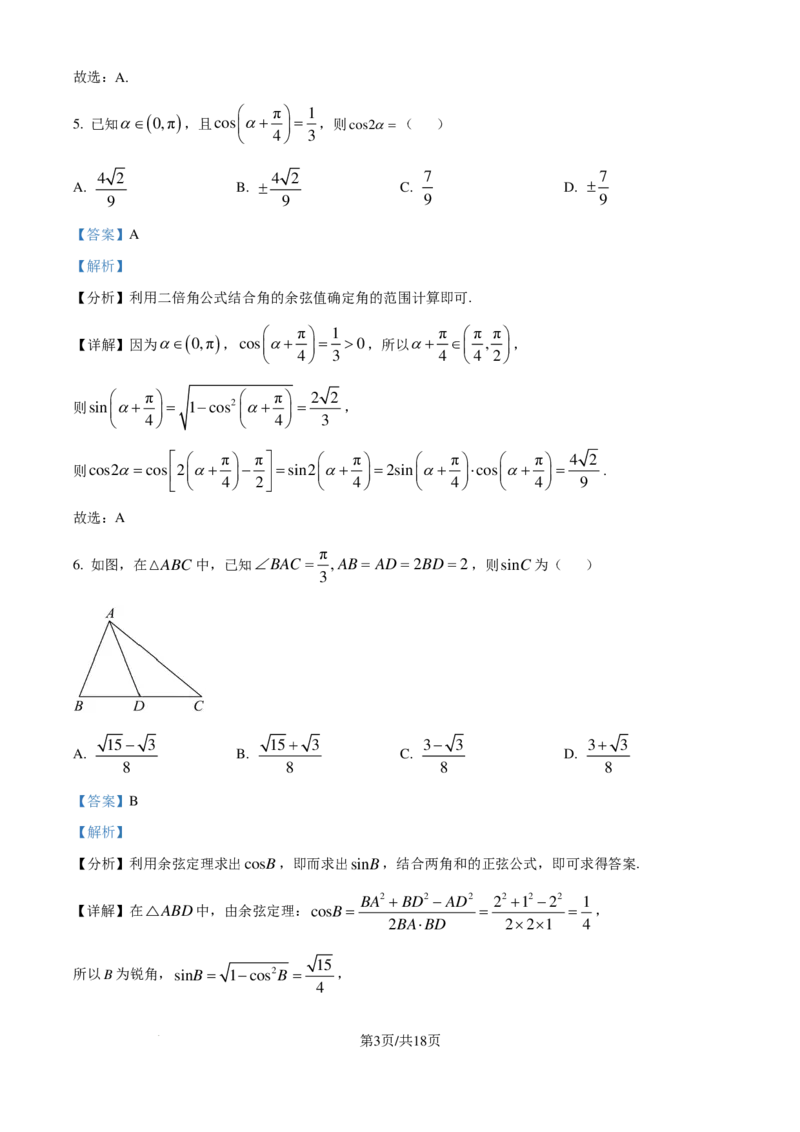  4 2  4  4  4 9 故选：A π 6. 如图，在ABC中，已知∠BAC = ,AB= AD=2BD=2，则sinC为（ ） 3 15− 3 15+ 3 3− 3 3+ 3 A. B. C. D. 8 8 8 8 【答案】B 【解析】 【分析】利用余弦定理求出cosB，即而求出sinB，结合两角和的正弦公式，即可求得答案. 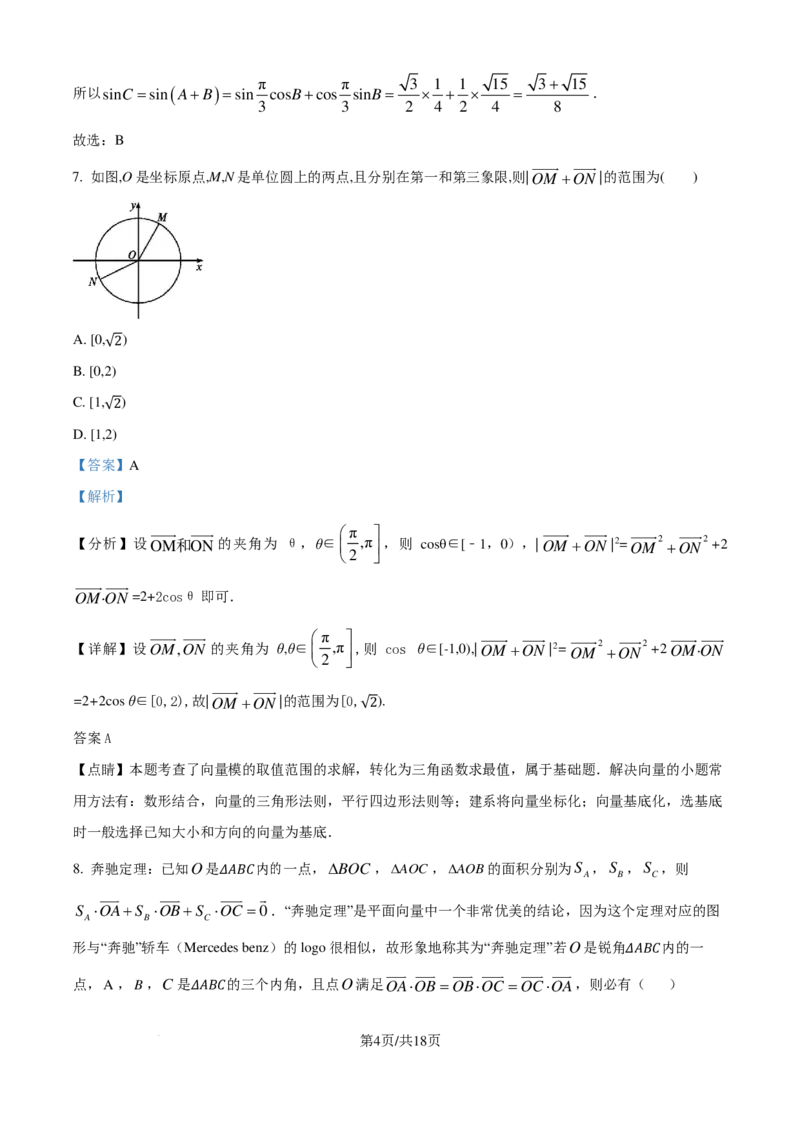BA2 +BD2 −AD2 22 +12 −22 1 【详解】在△ABD中，由余弦定理：cosB= = = ， 2BA⋅BD 2×2×1 4 15 所以B为锐角，sinB= 1−cos2B = ， 4 第3页/共18页 学科网（北京）股份有限公司π π 3 1 1 15 3+ 15 所以sinC =sin ( A+B )=sin cosB+cos sinB= × + × = ． 3 3 2 4 2 4 8 故选：B   7. 如图,O是坐标原点,M,N是单位圆上的两点,且分别在第一和第三象限,则|OM +ON|的范围为( ) A. [0, ) B. [0,2√)2 C. [1, ) D. [1,√2)2 【答案】A 【解析】   π      【分析】设OM和ON的夹角为 θ，θ∈ ,π  ，则 cosθ∈[﹣1，0），|OM +ON |2=OM 2 +ON 2 +2 2   OM·ON =2+2cosθ即可．   π       【详解】设OM,ON 的夹角为 θ,θ∈ ,π  ,则 cos θ∈[-1,0),|OM +ON |2=OM 2 +ON 2 +2OM·ON 2    =2+2cos θ∈[0,2),故|OM +ON|的范围为[0, ). 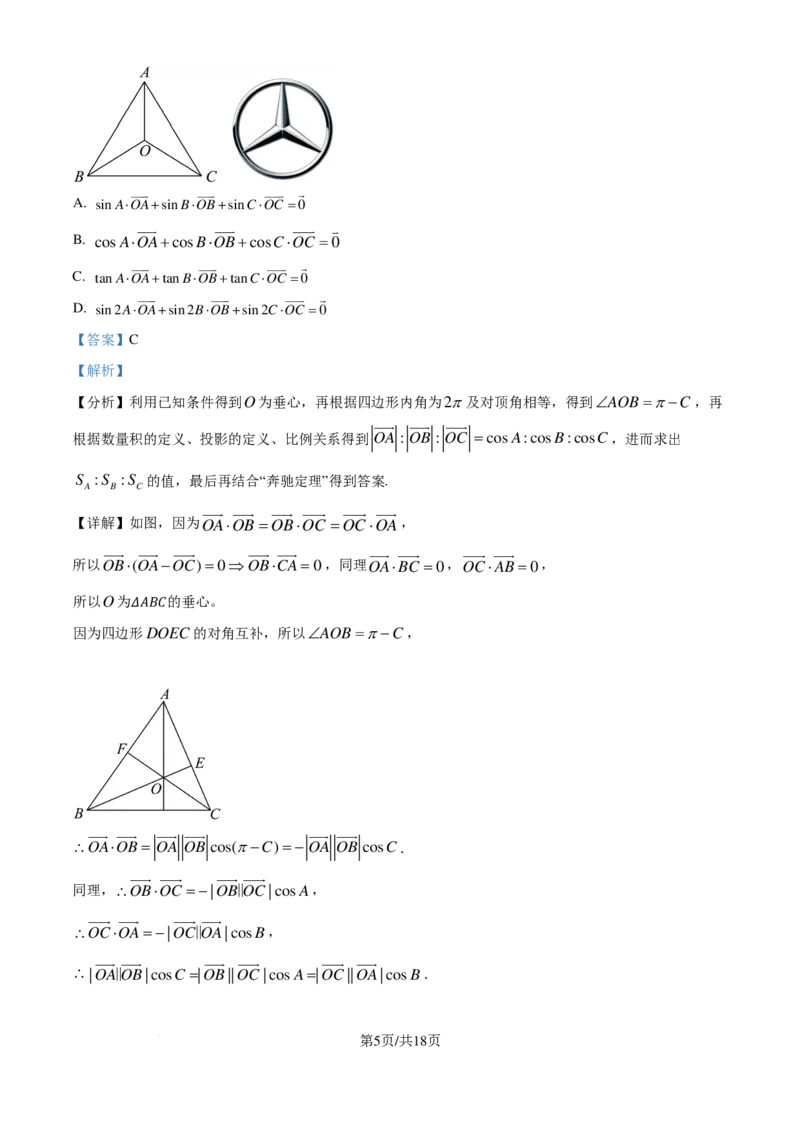答案A √2 【点睛】本题考查了向量模的取值范围的求解，转化为三角函数求最值，属于基础题．解决向量的小题常 用方法有：数形结合，向量的三角形法则，平行四边形法则等；建系将向量坐标化；向量基底化，选基底 时一般选择已知大小和方向的向量为基底． 8. 奔驰定理：已知O是 内的一点，∆BOC，∆AOC，∆AOB的面积分别为S ，S ，S ，则 A B C     𝛥𝛥𝛥𝛥𝛥𝛥𝛥𝛥 S ⋅OA+S ⋅OB+S ⋅OC =0．“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图 A B C 形与“奔驰”轿车（Mercedes benz）的logo很相似，故形象地称其为“奔驰定理”若O是锐角 内的一       点，A，B，C是 的三个内角，且点O满足OA⋅OB=OB⋅OC =OC⋅OA，则必有𝛥𝛥（𝛥𝛥𝛥𝛥 𝛥𝛥 ） 𝛥𝛥𝛥𝛥𝛥𝛥𝛥𝛥 第4页/共18页 学科网（北京）股份有限公司    A. sinA⋅OA+sinB⋅OB+sinC⋅OC =0     B. cosA⋅OA+cosB⋅OB+cosC⋅OC =0     C. tanA⋅OA+tanB⋅OB+tanC⋅OC =0     D. sin2A⋅OA+sin2B⋅OB+sin2C⋅OC =0 【答案】C 【解析】 【分析】利用已知条件得到O为垂心，再根据四边形内角为2π及对顶角相等，得到∠AOB=π−C，再    根据数量积的定义、投影的定义、比例关系得到 OA : OB : OC =cosA:cosB:cosC，进而求出 S :S :S 的值，最后再结合“奔驰定理”得到答案. A B C       【详解】如图，因为OA⋅OB=OB⋅OC =OC⋅OA，          所以OB⋅(OA−OC)=0⇒OB⋅CA=0，同理OA⋅BC =0，OC⋅AB=0， 所以O为 的垂心。 因为四边形𝛥𝛥𝛥𝛥D𝛥𝛥O𝛥𝛥EC的对角互补，所以∠AOB=π−C，       ∴OA⋅OB= OA OB cos(π−C)=− OA OB cosC．     同理，∴OB⋅OC =−|OB‖OC|cosA，     ∴OC⋅OA=−|OC‖OA|cosB，       ∴|OA‖OB|cosC =|OB||OC|cosA=|OC||OA|cosB． 第5页/共18页 学科网（北京）股份有限公司      |OA‖OB|cosC |OB||OC|cosA |OC||OA|cosB ∴    =    =    ， |OA‖OB||OC| |OA‖OB||OC| |OA‖OB||OC|    ∴OA : OB : OC =cosA:cosB:cosC．     1 1 又S = OB OC sin(π−A)= OB OC sin A A 2 2     1 1 S = OA OC sin(π−B)= OA OC sinB B 2 2     1 1 S = OB OAsin(π−C)= OB OAsinC C 2 2 sinA sinB sinC ∴S A :S B :S C =  :  :  = sinA : sinB : sinC =tan A:tanB:tanC． OA OB OC cosA cosB cosC     由奔驰定理得tan A⋅OA+tanB⋅OB+tanC⋅OC =0. 故选C． 【点睛】本题考查平面向量新定义，考查逻辑推理能力和运算求解能力，求解过程中要注意连比式子的变 形运用，属于难题. 二、多选题（本大题有 3个小题，每小题 6分，全部选对得 6分，错选不得分） 9. （多选）下列命题中，正确的是（ ） A. 在ABC中，A> B，则sinA>sinB B. 在锐角ABC中，不等式sin A>cosB恒成立 C. 在ABC中，若acosA＝bcosB，则ABC必是等腰直角三角形 D. 在ABC中，若B=60°，b2 =ac，则ABC必是等边三角形 【答案】ABD 【解析】 π π 【分析】A应用正弦定理及三角形中大边对大角即可判断正误；B由锐角三角形易得 > A> −B>0， 2 2 根据锐角正弦函数的大小关系及诱导公式即可判断正误；C由正弦定理边角关系，结合三角形内角的性质 判断内角A、B的数量关系；D利用余弦定理，结合已知得(a−c)2 =0，进而判断ABC的形状. a b 【详解】A：若sinA>sinB，而 = ，即a>b，故A> B，正确； sinA sinB 第6页/共18页 学科网（北京）股份有限公司π π π π B：由锐角ABC知：A+B> ，即 > A> −B>0，则sinA>sin( −B)=cosB，正确； 2 2 2 2 π C：由题设sinAcosA=sinBcosB，可得sin2A=sin2B，又A,B∈(0,π)，则A= B或A+B= ，故 2 ABC为等腰或直角三角形，错误； D：由题设，b2 =ac=a2 +c2 −ac，故(a−c)2 =0，即a =c，又B=60°，可知a=b=c，故ABC 必是等边三角形，正确. 故选：ABD  x+ y  x− y 10. 定义域为 的函数 f ( x ) 满足：∀x,y∈R, f ( x ) f ( y )= f 2   − f 2  ，当x>0时，  2   2  𝑅𝑅 f ( x )<0，则下列结论正确的有（ ） A. f ( 0 )=1 B. y = f ( x+1 )−2的图象关于点 (−1,−2 ) 对称 f ( 2023 )+ f ( 2025 ) f ( 2024 ) C. = f ( 2022 )+ f ( 2024 ) f ( 2023 ) ( ) D. f x 在 上单调递增 【答案】BC ( 0,+∞) 【解析】 【分析】对于A，赋值令x= y =0，求解；对于B，赋值令y =−x，得到 f(x)关于 ( 0,0 ) 对称，再结合 函数图像平移变换得解；对于C,赋值令x= y+2，再令y =2022,2023，再变形即可；对于D，赋值令 x=4,y =2，结合x>0时， f ( x )<0，举反例可解. 【详解】令x= y =0，得到 f 2( 0 )=0，则 f ( 0 )=0.故A错误. 令y =−x，得到 f ( x ) f (−x )= f 2( 0 )− f 2( x ) ， 则 f ( x ) f (−x )+ f 2( x )=0， f(x)(f(−x)+ f(x))=0 则 f(x)=0或 f(x) f(x)0, 由于当x>0时， f ( x )<0，则此时 f(x) f(x)0， 故x<0时， f ( x )>0，故x≠0时， f ( x )≠0，所以 f(x) f(x)0， 第7页/共18页 学科网（北京）股份有限公司而 f ( 0 )=0，故 f(x) f(x)0对任意x∈R恒成立，则 f(x)关于 ( 0,0 ) 对称. y = f ( x+1 )−2可由 f(x)向左平移1个单位，再向下平移2个单位. 则y = f ( x+1 )−2的图象关于点 (−1,−2 ) 对称，故B正确.  y+2+ y 令x= y+2，得到 f ( y+2 ) f ( y )= f 2   − f 2( 1 ) ，  2  则 f ( y+2 ) f ( y )= f 2( y+1 )− f 2( 1 ) . 令y =2022，得到 f ( 2024 ) f ( 2022 )= f 2( 2023 )− f 2( 1 ) 令y =2023，得到 f ( 2025 ) f ( 2023 )= f 2( 2024 )− f 2( 1 ) ， 两式相减得 f ( 2024 ) f ( 2022 )− f ( 2025 ) f ( 2023 )= f 2( 2023 )− f 2( 2024 ) ， 变形 f ( 2024 ) f ( 2022 )+ f 2( 2024 )= f ( 2025 ) f ( 2023 )+ f 2( 2023 ) ， 即 f ( 2024 )( f ( 2022 )+ f ( 2024 )) = ( f ( 2025 )+ f ( 2023 )) f ( 2023 ) , x>0时， f ( x )<0，两边除以 ( f ( 2022 )+ f ( 2024 )) f ( 2023 ) ， f ( 2023 )+ f ( 2025 ) f ( 2024 ) 即 = ，故C正确. f ( 2022 )+ f ( 2024 ) f ( 2023 ) 令x=4,y =2，则 f ( 4 ) f ( 2 )= f 2( 3 )− f 2( 1 )= ( f ( 3 )+ f ( 1 ))( f ( 3 )− f ( 1 )) ， x>0时， f ( x )<0，则 f ( 4 ) f ( 2 )= ( f ( 3 )+ f ( 1 ))( f ( 3 )− f ( 1 )) >0， 且 f ( 3 )+ f ( 1 )<0，则 f ( 3 )− f ( 1 )<0，即 f ( 3 )< f ( 1 ) .故D错误. 故选：BC. 【点睛】难点点睛：解答此类有关函数性质的题目，难点在于要结合抽象函数性质，利用赋值法以及代换 法，推出函数相应的性质. 11. 围棋是我国发明的古老的也是最复杂的智力竞技活动之一.现代围棋棋盘共有19行19列，361个格 点，每个格点上可能出现黑子､白子､空三种情况，因此整个棋盘上有3361种不同的情况，下面对于数字 3361的判断正确的是（ ） （参考数据：lg3≈0.4771） A. 3361的个位数是3 B. 3361的个位数是1 第8页/共18页 学科网（北京）股份有限公司C. 3361是173位数 D. 3361是172位数 【答案】AC 【解析】 【分析】对于AB，因为31,32,33,34,35,的个位数以4为周期循环往复，则3361的个位数与31的个位数相 同，即可判断AB；对于CD，通过对数运算lg3361 =361lg3≈172.2331，得3361 ≈100.2331×10172即可判断 CD. 【详解】对于AB,由31 =3,32 =9,33 =27,34 =81,35 =243,， 个位数分别为3,9,7,1,3,9,7，以4为周期循环往复， 因为361÷4的余数为1， 故3361的个位数与31的个位数相同， 即3361的个位数为3，故A正确，B错误； 对于CD，因为lg3361 =361lg3≈361×0.4771=172.2331， 所以3361 ≈10172.2331 =100.2331×10172， 因为100.2331∈( 1,2 ) ， 所以3361为173位数，故C正确，D错误. 故选：AC. 三、填空题（本题共 3题，每题 5分，共 15分） 12. f ( x ) 的周期为2，值域为 [ 0,1 ] ，且为偶函数，则 f ( x ) 的解析式 f ( x )=__________.（写出一个即 可） 1 1 【答案】 cos ( πx )+ (答案不唯一） 2 2 【解析】 1 1 【分析】取 f ( x )= cos ( πx )+ ，再验证周期，值域和奇偶性得到答案. 2 2 1 1 【详解】取 f ( x )= cos ( πx )+ ， 2 2 2π 1 1 则函数周期为T = =π，cos ( πx )∈[−1,1 ] ， f ( x )= cos ( πx )+ ∈[ 0,1 ]， 2 2 2 1 1 1 1 f (−x )= cos (−πx )+ = cos ( πx )+ = f ( x )，函数为偶函数，满足条件. 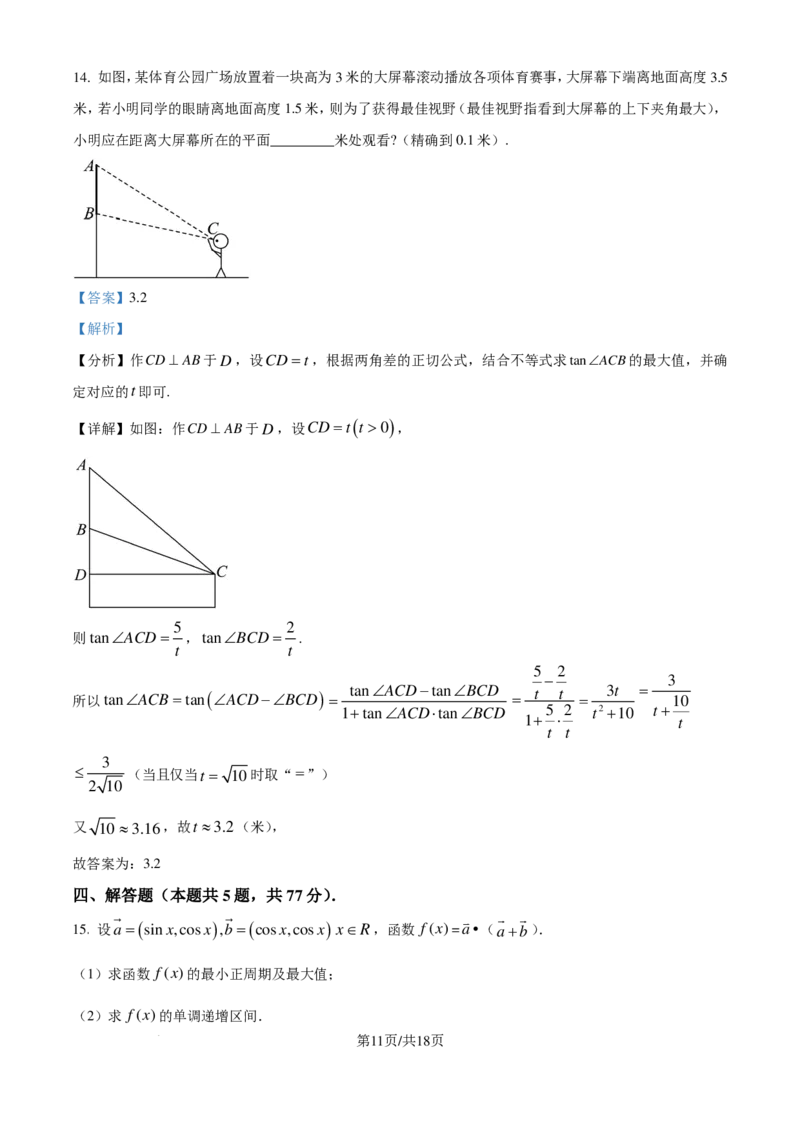2 2 2 2 第9页/共18页 学科网（北京）股份有限公司1 1 故答案为： cos ( πx )+ 2 2 13. 用M 表示函数y =sinx在闭区间I上的最大值．若正数a满足M ≥2M ，则a的最大值为 I [0,a] [a,2a] ________． 13 【答案】 π 12 【解析】 【分析】分类讨论，根据正弦函数的图象与性质求出M 、M ，代入不等式求解a的取值范围即可. [0,a] [a,2a] π 【详解】①当a∈[0, )时，2a∈[0,π),M =sina,M =1， [0,a] [a,2a] 2 若M ≥2M ，则sina≥2，此时不成立； [0,a] [a,2a] π ②当a∈[ ,π)时，2a∈[π,2π),M =1,M =sina， [0,a] [a,2a] 2 1 π 5π 若M ≥2M ，则1≥2sina⇒sina≤ ，又a∈[ ,π)，解得a∈[ ,π)； [0,a] [a,2a] 2 2 6 3π ③当a∈[π, )时，2a∈[2π,3π),M =1,M =sin2a， [0,a] [a,2a] 2 1 3π 13π 若M ≥2M ，则1≥2sin2a⇒sin2a≤ ，又a∈[π, )，解得a∈[π, ]； [0,a] [a,2a] 2 2 12 3π ④当a∈[ ,+∞)时，2a∈[3π,+∞)，M =1，M =1，不符合题意. [0,a] [a,2a] 2 5π 13π 13 综上所述，a∈[ , ]，即a的最大值为 π. 6 12 12 13 故答案为： π 12 【点睛】本题考查正弦函数的图象与性质，考查逻辑推理能力、直观想象能力，属于中档题. 第10页/共18页 学科网（北京）股份有限公司14. 如图，某体育公园广场放置着一块高为3米的大屏幕滚动播放各项体育赛事，大屏幕下端离地面高度3.5 米，若小明同学的眼睛离地面高度1.5米，则为了获得最佳视野（最佳视野指看到大屏幕的上下夹角最大）， 小明应在距离大屏幕所在的平面_________米处观看?（精确到0.1米）. 【答案】3.2 【解析】 【分析】作CD⊥ AB于D，设CD=t，根据两角差的正切公式，结合不等式求tan∠ACB的最大值，并确 定对应的t即可. 【详解】如图：作CD⊥ AB于D，设CD=t ( t >0 ) ， 5 2 则tan∠ACD= ，tan∠BCD= . t t 5 2 − 3 所以tan∠ACB=tan (∠ACD−∠BCD ) = tan∠ACD−tan∠BCD = t t = 3t = 10 1+tan∠ACD⋅tan∠BCD 5 2 t2 +10 t+ 1+ ⋅ t t t 3 ≤ （当且仅当t = 10时取“=”） 2 10 又 10 ≈3.16，故t ≈3.2（米）， 故答案为：3.2 四、解答题（本题共 5题，共 77分）．      15. 设a=( sinx,cosx ) ,b=( cosx,cosx ) x∈R，函数 f(x)=a•（a+b）． （1）求函数 f(x)的最小正周期及最大值； （2）求 f(x)的单调递增区间． 第11页/共18页 学科网（北京）股份有限公司3+ 2 3π π 【答案】（1）最小正周期为π，最大值为 ； （2）[− +kπ, +kπ],k∈Z . 2 8 8 【解析】 【分析】 ( ) （1）根据向量的数量积的运算和三角恒等变换的公式，求得函数 f x 的解析式，结合三角函数的性质， 即可求解； ( ) （2）由（1）中函数 f x 的解析式，结合正弦型函数的性质，即可求解.   【详解】由题意，向量a =( sinx,cosx ) ,b=( cosx,cosx ) x∈R，       可得函数 f ( x )=a⋅(a+b)=a 2 +a⋅b=sin2 x+cos2 x+sinxcosx+cos2 x 1 1+cos2x 1 1 3 2 π 3 =1+ sin2x+ = sin2x+ cos2x+ = sin(2x+ )+ ， 2 2 2 2 2 2 4 2 2π 所以函数 f(x)的最小正周期为T = =π， 2 π π π 3+ 2 当2x+ = +2kπ,k∈Z时，即x= +kπ,k∈Z ，函数取得最大值，最大值为 . 4 2 8 2 2 π 3 （2）由（1）知，函数 f ( x )= sin(2x+ )+ ， 2 4 2 π π π 3π π 令− +2kπ≤2x+ ≤ +2kπ,k∈Z ，解得− +kπ≤ x≤ +kπ,k∈Z ， 2 4 2 8 8 3π π 所以函数 f ( x ) 的单调递增区间为[− +kπ, +kπ],k∈Z . 8 8 【点睛】本题主要考查了平面向量的数量积的运算，三角恒等变换的化简运算，以及三角函数的图象与性 质的应用，着重考查了推理与运算能力，属于中档试题. 16. 已知函数 f(x)= mx+n 是定义在[−1,1]上的奇函数，且 f ( 1 )=1. x2 +1 （1）求m，n的值： （2）试判断函数 f(x)的单调性，并证明你的结论； （3）求使 f ( a−1 )+ f ( a2 −1 ) <0成立的实数a的取值范围. 【答案】（1）m=2，n=0 2x （2） f(x)= 在[−1,1]上为增函数.证明见解析 x2 +1 [ ) （3） 0,1 第12页/共18页 学科网（北京）股份有限公司【解析】 【分析】（1）由奇函数的性质可得 f(0)=0，结合 f ( 1 )=1，解方程可得m，n的值； （2） f(x)在 [−1,1 ] 上为增函数，再由单调性的定义证明，注意运用因式分解和不等式的性质； （3）由奇函数 f(x)在[−1,1]上为增函数，可将不等式的两边的“ f ”去掉，解不等式可得所求取值范围. 【小问1详解】 由题意，x∈[−1,1] mx+n 在 f(x)= 中，函数是奇函数， x2 +1 且 f ( 1 )=1，可得 f(0)=0即n=0； 1 又 (m+n)=1，则m=2， 2 ∴m=2，n=0；经验证满足题意. 【小问2详解】 由题意及（1）得， 2x f(x)= 在[−1,1]上为增函数.证明如下： x2 +1 mx+n 在 f(x)= 中，x∈[−1,1] x2 +1 2x 2x 2(x −x )(1−x x ) 设−1x 1 0 1 故有：cosB=− 2 2π 又B∈( 0,π ) ，则B= 3 2π 故∠B的大小为： 3 【小问2详解】 若选①： 由BD平分∠ABC得：S =S +S △ABC △ABD △BCD 1 2π 1 π 1 π 则有： acsin = ×1×csin + ×1×asin ，即ac=a+c 2 3 2 3 2 3 第14页/共18页 学科网（北京）股份有限公司2π 在ABC中，由余弦定理可得：b2 =a2 +c2 −2accos 3 又b=2 3，则有：a2 +c2 +ac=12 ac=a+c 联立 a2 +c2 +ac=12 可得：(ac)2 − ac− 12 = 0 解得：ac=4（ac=−3舍去） 1 2π 1 3 故S = acsin = ×4× = 3 △ABC 2 3 2 2 若选②： → 1 → →  → 2 1 → →  2 1 → 2 → → → 2 可得：BD= BA+BC，BD = BA+BC = BA +2BA⋅BC+BC  2  4  4  1 2π  1= c2 +2accos +a2 ，可得：a2 +c2 −ac =4 4 3  2π 在ABC中，由余弦定理可得：b2 =a2 +c2 −2accos ，即a2 +c2 +ac=12 3 a2 +c2 −ac=4 联立 a2 +c2 +ac=12 解得：ac=4 1 2π 1 3 故S = acsin = ×4× = 3 △ABC 2 3 2 2  π 18. 已知函数 f(x)= Asin(ωx+ϕ)+BA>0,ω>0,|ϕ|< 的某一周期内的对应值如下表：  2 π π 5π 4π 11π x − 6 3 6 3 6 f(x) −1 1 3 1 −1 （1）根据表格提供的数据求函数 f(x)的解析式； 2π  π （2）根据（1）的结果，若函数y = f(nx)，n>0的最小正周期为 ，当x∈  0,  时，方程 3  3 第15页/共18页 学科网（北京）股份有限公司f(nx)=m恰有两个不同的解，求实数m的取值范围．  π 【答案】（1） f(x)=2sinx−  +1  3  （2）[ 3+1,3) 【解析】 【分析】（1）根据表格提供数据依次求得ω,ϕ,A,B的值，从而求得解析式； （2）先利用周期公式求n的值，利用换元法，结合三角函数的图象求得m的取值范围. 【小问1详解】 2π 设 f(x)的最小正周期为T，则T＝2π，由T = 得ω＝1， ω B+ A=3 A=2 又由 ，解得 ， B−A=−1 B=1 5π π 令ω⋅ +ϕ= +2kπ,k∈Z， 6 2 5π π π 即 +ϕ= +2kπ,k∈Z，解得ϕ=− +2kπ,k∈Z， 6 2 3 π π  π 因为ϕ< ，所以ϕ=− ，所以 f(x)=2sinx−  +1. 2 3  3 【小问2详解】  π f(nx)=2sinnx−  +1，  3  π 2π 因为函数 f(nx)=2sinnx−  +1的最小正周期为 ，且n>0，∴n＝3，  3 3 π  π π  π 2π 令t =3x− ，由x∈  0,  得t =3x− ∈  − ,  ， 3  3 3  3 3  m−1 所以由2sint+1=m恰有两个不同的解，得sint = 有两个交点， 2  π 2π m−1 如图所示，当t∈  − ,  时，且函数图象y =sint和 y = 有两个交点时，  3 3  2 m−1  3  sint = ∈ ,1，  2  2  ) 解得：m∈ 3+1,3 .  第16页/共18页 学科网（北京）股份有限公司19. 如图，矩形ABCD中，AB=2 3，BC =4，点M ，N 分别在线段AB，CD(含端点)上，P为 AD的中点，PM ⊥PN ，设∠APM =α. （1）求角α的取值范围； （2）求出PMN 的周长l关于角α的函数解析式 f(α)，并求PMN 的周长l的最小值及此时α的值. π π 【答案】（1）[ , ]； （2）4( 2+1). 6 3 【解析】 π 【分析】（1）由题意，当点M 位于点B时，角α取最大值，得到α= ，当点N 位于点C时，∠DPN 3 π 取得最大值，角α取最小值，求得α = ，即可求解. min 6 2 2 （2）在直角△PAM 中，求得PM = ，在直角△PDN 中，求得PN = ，在PMN 中，由勾 cosα sinα 2 2(1+sinα+cosα) π π 股定理求得MN = ，得到 f (α)= ,α∈[ , ]，利用换元法和三角函数 cosαsinα sinαcosα 6 3 的性质，结合函数的单调性，即可求解. 【详解】（1）由题意，当点M 位于点B时，角α取最大值，此时tanα= 3， π π 因为0<α< ，所以α= ， 2 3 当点N 位于点C时，∠DPN 取得最大值，角α取最小值， π π π π 由对称性知此时∠DPN = ，所以α = − = ， 3 min 2 3 6 π π 所以角α的取值范围是[ , ]. 6 3 第17页/共18页 学科网（北京）股份有限公司PA 2 （2）在直角△PAM 中，cosα= 且PA=2，所以PM = ， PM cosα π PD 2 在直角△PDN 中，cos∠PDN =cos( −α)=sinα= 且PD=2，所以PN = ， 2 PN sinα 4 4 4 在PMN 中，由勾股定理得MN2 = PM2 +PN2 = + = ， cos2α sin2α cos2αsin2α π π 2 因为α∈[ , ]，所以sinα>0,cosα>0，所以MN = ， 6 3 cosαsinα 2 2 2 2(1+sinα+cosα) π π 所以 f (α)= + + = ,α∈[ , ]， sinα cosα sinαcosα sinαcosα 6 3 π 令t =sinα+cosα= 2sin(α+ )， 4 π π π 5π 7π π 3+1 因为α∈[ , ]，可得α+ ∈[ , ]，所以t = 2sin(α+ )∈[ , 2]， 6 3 4 12 12 4 2 2 ( t+1 ) 4 t2 −1 g ( t )= = 又由sinαcosα= ，可得 t2 −1 t−1， 2 2 ( ) 3+1 因为函数g t 在区间[ , 2]上单调递减， 2 4 ( ) π π 当t = 2 时，g ( t ) = =4 2+1 ，此时t = 2sin(α+ )= 2 ，解得α= ， min 2−1 4 4 π 所以当α= 时，PMN 的周长l取得最小值，最小值为4( 2+1). 4 【点睛】解答三角函数的图象与性质的基本方法： 1、根据已知条件化简得出三角函数的解析式为 的形式； 2、熟练应用三角函数的图象与性质，结合数形结合法的思想研究函数的性质（如：单调性、奇偶性、对 称性、周期性与最值等），进而加深理解函数的极值点、最值点、零点及有界性等概念与性质，但解答中 主要角的范围的判定，防止错解. 第18页/共18页 学科网（北京）股份有限公司