文档内容
微信公众号“做事方法很重要”
洛阳市 ——— 学年高一质量检测
2024 2025
数学试卷参考答案
一、选择题
1-4. CDBD 5-8. ABCD
二、选择题
9. ABC 10. AC 11. BCD
三、填空题
1 41
12. 1 13. 14. π
2 2
四、解答题
. 分
15 (12 )
由已知得 z = m2 - m + + m2 - m + ′
(1) , 3 2 ( 4 3)i, ……1
z为纯虚数
∵ ,
{m2 - m + = ′
3 2 0, ……2
∴ m2 - m + ′
4 3≠0, ……3
m = . ′
∴ 2 ……4
设A t t < 则O→A = t ′
(2) (0, )( 0), (0, ), ……5
又O→Z = m2 - m + m2 - m + ′
( 3 2, 4 3), ……6
由O→A O→Z夹角为锐角得
, :
O→A O→Z > 且O→A与O→Z不共线 ′
· 0, , ……8
{t m2 - m + > ′
( 4 3) 0, ……9
∴ m2 - m + . ′
3 2≠0 ……10
解得 < m < 且m
1 3 ≠2,
故m的取值范围为 . ′
(1,2) ∪(2,3) ……12
. 分
16 (13 )
由于 4x - x x - 4x = 2x + 2x 2x - 2x - x x
(1) cos 2 3sin cos sin (cos sin )(cos sin ) 2 3sin cos
= x - x = x + π
cos2 3sin2 2cos(2 ),
3
高一数学答案 第 页 共 页
1 ( 5 ) (2025.7)
微信公众号“做事方法很重要”微信公众号“做事方法很重要”
f x = x + π ′
∴ ( ) 2cos(2 ), ……4
3
由 k - x + π k 得
(2 1)π ≤2 ≤2 π :
3
- 2π + k x - π + k ′
π ≤ ≤ π, ……6
3 6
故f x 的单调递增区间为 - 2π + k - π + k k Z ′
( ) [ π, π]( ∈ ), ……7
3 6
x π 时 x + π π 4π ′
(2) ∈[0, ] ,2 ∈[ , ], ……8
2 3 3 3
当 x + π π 即x π 时 f x 单调递减 ′
2 ∈[ ,π], ∈[0, ] , ( ) , ……10
3 3 3
当 x + π 4π 即x π π 时 f x 单调递增 ′
2 ∈[π, ], ∈[ , ] , ( ) , ……12
3 3 3 2
故当x = π 时 f x 有最小值 且f x = f π =- ′
, ( ) , ( )min ( ) 2, ……13
3 3
. 分 本试卷答案最早发在微信公众号“做事方法很重要”
17 (13 )
用x x 分别表示第 次取到的球 则可用 x x 表示 次取球的可能结果
(1) 1, 2 1,2 , ( 1, 2) 2 ,
则样本空间Ω = R R R G R G R R G R G R . ′
{( 1, 2),( 1, ),( 2, ),( 2, 1),( , 1),( , 2)} ……4
样本点总数为 + n + n 两个球都是红球的样本点个数为 × =
(2)① (3 )(2 ), 3 2 6,
故 6 = 1 解得n = . ′
+ n + n , 4 ……8
(3 )(2 ) 7
设A = 第一次取到红球 B = 第二次取到红球
② “ ”, “ ”,
- - - -
则 取到的 个球颜色不同 = AB AB 且AB 与 AB互斥
“ 2 ” ∪ , ,
- - - -
所以P AB AB = P AB + P A = 12 + 12 = 4 . ′
( ∪ ) ( ) ( B) ……13
42 42 7
. 分 本试卷答案最早发在微信公众号“做事方法很重要”
18 (13 )
b B C + c B + C = a 由正弦定理得
∵ 2 cos cos cos2 , :
B B C + C B + C = A ′
2sin cos cos sin cos2 sin sin , ……2
B B C + 2B C = A ′
∴ 2sin cos cos 2cos sin sin , ……3
B B C + B C = A
∴ 2cos (sin cos cos sin ) sin ,
B B + C = A ′
∴ 2cos sin( ) sin , ……5
高一数学答案 第 页 共 页
2 ( 5 ) (2025.7)
微信公众号“做事方法很重要”微信公众号“做事方法很重要”
即 B A = A 又 A >
2cos sin sin , sin 0,
B = 1
∴ cos ,
2
B
∵ ∈(0,π),
B = π . ′
∴ ……7
3
设BD = m 则由S + S = S 知
(2) , △ ABD △ CBD △ ABC
1 π + 1am π = 1ac π ′
cmsin sin sin , ……10
2 6 2 6 2 3
a + c
× 2
ac 3 ( )
m = 3 2 = 3 a + c = 3 × = ′
∴ a + c≤ a + c ( ) 4 3, ……12
4 4
当且仅当a = c = 时 取 =
2 , “ ”,
故BD长度的最大值为 ′
3, ……13
. 分 本试卷答案最早发在微信公众号“做事方法很重要”
19 (13 )
方程f x = 1 即 x = 1
( ) x , e x ,
当x < 时 方程ex = 1 无实数解. ′
0 , x ……1
当x > 时 令φ x = x - 1 则φ x 在 + 上单调递增 ′
0 , ( ) e x , ( ) (0, ∞) , ……2
又φ 1 = - < φ = - > .
( ) e 2 0, (1) e 1 0
2
故φ x 在 1 内有唯一零点x
( ) ( ,1) 0,
2
即x 1 . ′
0 ∈( ,1) ……4
2
x - x -
x 0 + x - = 1 + x - = ( 0 1)(2 0 1) <
∴ e 2 0 3 x 2 0 3 x 0
0 0
x
0 + x < . ′
∴ e 2 0 3 ……5
g x = x ′
(2) ( ) ln , ……6
h x = x + e-x ′
∴ ( ) ln(e ), ……7
高一数学答案 第 页 共 页
3 ( 5 ) (2025.7)
微信公众号“做事方法很重要”微信公众号“做事方法很重要”
h x = g m x + 1 -x + m .
∵ ( ) ( e e 2 )
2
即 x + -x = m x + 1 -x + m
ln(e e ) ln( e e 2 ),
2
x + -x = m x + 1 -x + m ′
∴ e e e e 2 , ……8
2
m - 2 x + m x - 1 = .
∴ ( 1)e 2 e 0
2
令 x = t t >
e ( 0),
即 m - t2 + mt - 1 = 在 + 有两个不等实根 ′
( 1) 2 0 (0, ∞) , ……9
2
ìm -
ï
1≠0 ,
ï
ï m 2 - m - × - 1 >
ï(2 ) 4( 1) ( ) 0 ,
ï 2
í m
∴ ït + t = 2 >
ï1 2 - m 0 ,
1
ï
ï ït t =- 1 > .
î1· 2 m - 0
2( 1)
1 < m < 即m的取值范围为 1 . ′
∴ 1, ( ,1) ……13
2 2
. 分 本试卷答案最早发在微信公众号“做事方法很重要”
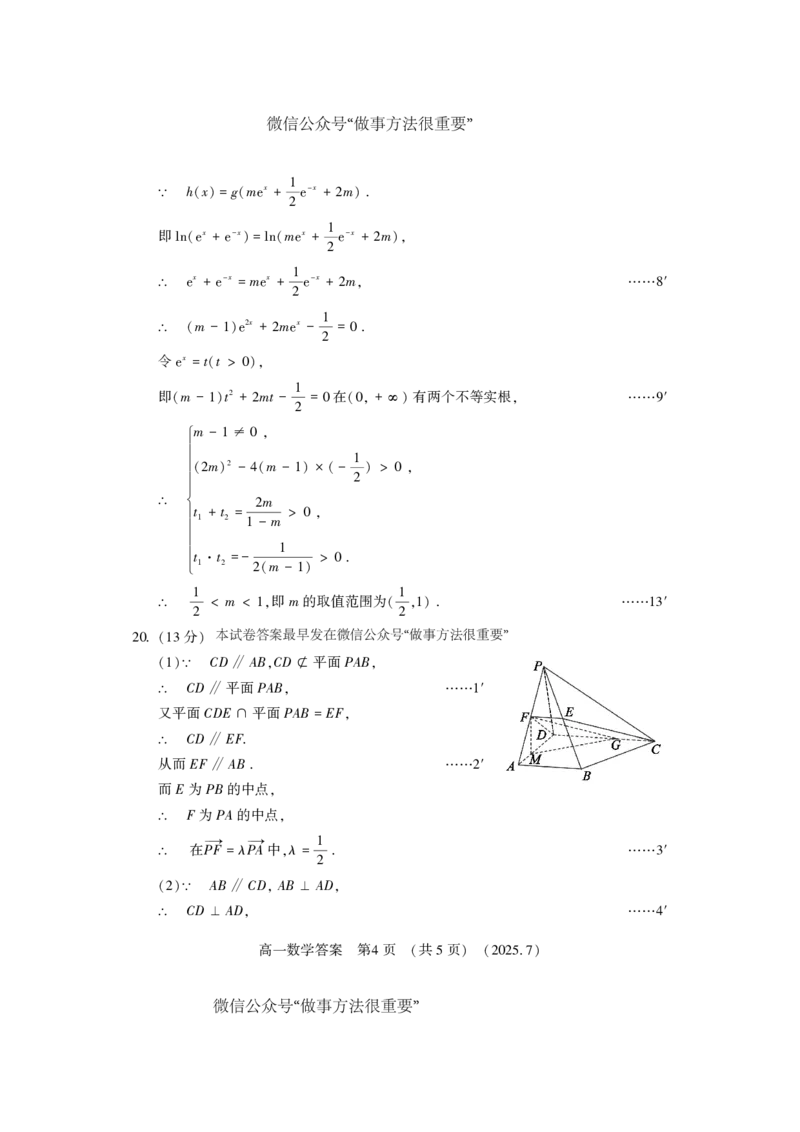
20 (13 )
CD AB CD 平面PAB
(1)∵ ∥ , ⊄ ,
CD 平面PAB ′
∴ ∥ , ……1
又平面CDE 平面PAB = EF
∩ ,
CD EF.
∴ ∥
从而EF AB . ′
∥ ……2
而E为PB的中点
,
F为PA的中点
∴ ,
在P→F = λP→A中 λ = 1 . ′
∴ , ……3
2
AB CD AB AD
(2)∵ ∥ , ⊥ ,
CD AD ′
∴ ⊥ , ……4
高一数学答案 第 页 共 页
4 ( 5 ) (2025.7)
微信公众号“做事方法很重要”微信公众号“做事方法很重要”
平面PAD 平面ABCD
∵ ⊥ ,
平面PAD 平面ABCD = AD
∩ ,
CD 平面PAD
∴ ⊥ ,
CD DF . ′
∴ ⊥ ……5
在直角梯形CDFE中 CD = EF = 3 DF = 3 6
, 6, , ,
2 2
故S = 1 × 3 + × 3 6 = 45 6 . ′
( 6) ……7
2 2 2 8
在CD上取靠近点C的四等分点G 连FG
(3) , ,
由EF CG知四边形CEFG为平行四边形
,
FG CE
∴ ∥ ,
FG与平面PAD所成的角等于CE与平面PAD所成的角 FG与平面ABCD所成的
∴ ,
角等于CE与平面ABCD所成的角. ′
……9
GD 平面PAD 本试卷答案最早发在微信公众号“做事方法很重要”
∵ ⊥ ,
GFD即为FG与平面PAD所成的角
∴ ∠ ,
在 GDF中 GD = 9 DF = 3 6
Rt△ , , ,
2 2
FG = 3 15
∴ ,
2
9
α GFD = 2 = 15 ′
∴ sin = sin∠ , ……11
3 15 5
2
作FM AD于M 则FM 平面ABCD
⊥ , ⊥ ,
连接GM 则 FGM即为FG与平面ABCD所成的角 .
, ∠
在Rt FGM中 FM = 3 15
△ , ,
4
FM
β = FGM = = 1 . ′
∴ sin sin∠ FG ……12
2
2α + 2β = 15 2 + 1 2 = 17 . ′
∴ sin sin ( ) ( ) ……13
5 2 20
高一数学答案 第 页 共 页
5 ( 5 ) (2025.7)
微信公众号“做事方法很重要”