文档内容
第九章 统计A(基础卷)
参考答案与试题解析
一.选择题(共8小题)
1.(2020春•郑州期中)某中学为了了解500名学生的身高,从中抽取了30名学生的身高进行统计分析,
在这个问题中,500名学生身高的全体是( )
A.总体
B.个体
C.从总体中抽取的一个样本
D.样本的容量
【解答】解:为了了解500名学生的身高,从中抽取了30名学生的身高进行统计分析,
这500名学生身高的全体是总体.
故选:A.
2.(2020春•盐城期末)某校高一、高二、高三年级各有学生数分别为800、1000、800(单位:人),现
用分层抽样的方法抽取一个容量为n的样本了解网课学习情况,样本中高一学生的人数为48人,那么
此样本的容量n为( )
A.108 B.96 C.156 D.208
【解答】解:∵高一、高二、高三学生的数量之比依次为800:1000:800=4:5:4,
现用分层抽样的方法抽出的样本中高一学生有48人,
∴由分层抽样性质,得: ,
解得n=156.
故选:C.
3.(2020•赣州模拟)从某班50名同学中选出5人参加户外活动,利用随机数表法抽取样本时,先将 50
名同学按01,02,……50进行编号,然后从随机数表的第1行第5列和第6列数字开始从左往右依次选
取两个数字,则选出的第5个个体的编号为( )(注:表为随机数表的第1行与第2行)
0347 4373 8636 9647 3661 4698 6371 6297
7424 6792 4281 1457 2042 5332 3732 1676
A.24 B.36 C.46 D.47
【解答】解:由题知从随机数表的第1行第5列和第6列数字开始,由表可知依次选取43,36,47,
46,24.故选:A.
4.(2020•山西模拟)如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:
分).则甲组数据的中位数,乙组数据的平均数分别为( )
A.12,15 B.15,15 C.15,15.9 D.15,16.8
【解答】解:由茎叶图得:
甲组数据为:
9,12,15,24,27,
乙组数据为:
8,15,18,19,24,
故甲组数据的中位数是15,
乙组数据的平均数是: 16.8,
故选:D.
5.(2020•新课标Ⅲ)设一组样本数据x ,x ,…,x 的方差为0.01,则数据10x ,10x ,…,10x 的方差
1 2 n 1 2 n
为( )
A.0.01 B.0.1 C.1 D.10
【解答】解:∵样本数据x ,x ,…,x 的方差为0.01,
1 2 n
∴根据任何一组数据同时扩大几倍方差将变为平方倍增长,
∴数据10x ,10x ,…,10x 的方差为:100×0.01=1,
1 2 n
故选:C.
6.(2020春•闵行区校级期中)在一次数学测试中,高二某班 40名学生成绩的平均分为82,方差为
10.2,则下列四个数中不可能是该班数学成绩的是( )
A.100 B.85 C.65 D.55
【解答】解:因为S2 10.2,
所以 40×10.2=408,
若存在x=55,则(x )2=(55﹣82)2=729 408,
则方差必然大于10.2,不符合题意,所以55不可能是所有成绩中的一个样本.
故选:D.
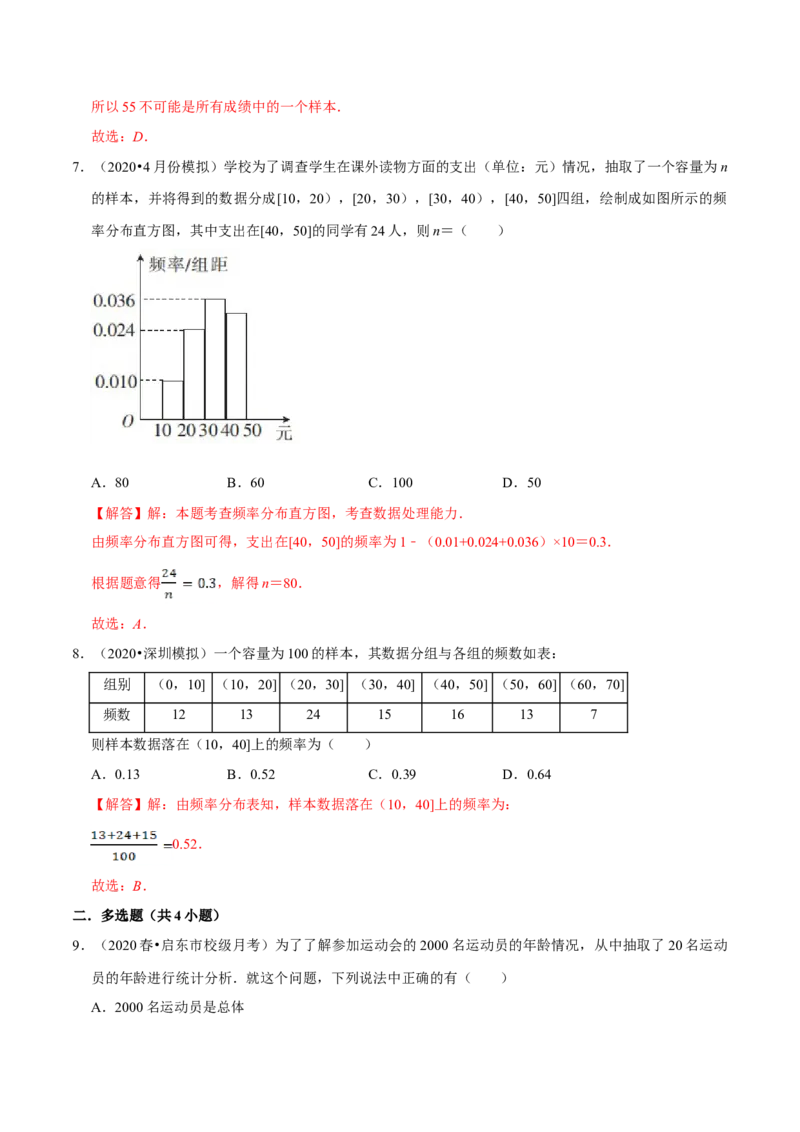
7.(2020•4月份模拟)学校为了调查学生在课外读物方面的支出(单位:元)情况,抽取了一个容量为n
的样本,并将得到的数据分成[10,20),[20,30),[30,40),[40,50]四组,绘制成如图所示的频
率分布直方图,其中支出在[40,50]的同学有24人,则n=( )
A.80 B.60 C.100 D.50
【解答】解:本题考查频率分布直方图,考查数据处理能力.
由频率分布直方图可得,支出在[40,50]的频率为1﹣(0.01+0.024+0.036)×10=0.3.
根据题意得 ,解得n=80.
故选:A.
8.(2020•深圳模拟)一个容量为100的样本,其数据分组与各组的频数如表:
组别 (0,10] (10,20] (20,30] (30,40] (40,50] (50,60] (60,70]
频数 12 13 24 15 16 13 7
则样本数据落在(10,40]上的频率为( )
A.0.13 B.0.52 C.0.39 D.0.64
【解答】解:由频率分布表知,样本数据落在(10,40]上的频率为:
0.52.
故选:B.
二.多选题(共4小题)
9.(2020春•启东市校级月考)为了了解参加运动会的2000名运动员的年龄情况,从中抽取了20名运动
员的年龄进行统计分析.就这个问题,下列说法中正确的有( )
A.2000名运动员是总体B.所抽取的20名运动员是一个样本
C.样本容量为20
D.每个运动员被抽到的机会相等.
【解答】解:由题意知,2000名运动员的年龄是总体,所以A错误;
所抽取的20名运动员的年龄是一个样本,所以A错误;
样本容量是20,所以C正确;
每个运动员被抽到的机会相等,所以D正确.
故选:CD.
10.(2020•烟台一模)2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延,疫情就是命令,防
控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢
疫情防控阻击战的人民战争.右侧的图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该
折线图,下列结论正确的是( )
A.16天中每新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数小于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000
D.19至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
【解答】解:由频率分布折线图可知,16天中新增确诊病例数量整体呈下降趋势,但具体到每一天有
增有减,故A错误;
由每日新增确诊病例的数量大部分小于新增疑似病例的数量,则 16天中每日新增确诊病例的中位数小
于新增疑似病例的中位数,故B正确;
由图可知,16天中新增确诊、新增疑似、新增治愈病例的极差均大于2000,故C正确;
由图可知,20日的新增治愈病例数量小于新增确诊与新增疑似病例之和,故D错误.
∴正确的结论是BC.
故选:BC.11.(2020春•济宁月考)一组数据2x +l,2x +1,2x +1,…,2x +1的平均值为7,方差为4,记3x +2,
1 2 3 n 1
3x +2,3x +2,…,3x +2的平均值为a,方差为b,则( )
2 3 n
A.a=7 B.a=ll C.b=12 D.b=9
【解答】解:2x +l,2x +1,2x +1,…,2x +1的平均值为7,方差为4,
1 2 3 n
设X=(x ,x ,x ,…,x ),
1 2 3 n
E(2X+1)=2E(X)+1=7,得E(X)=3,
D(2X+1)=4D(X)=4,D(X)=1,
3x +2,3x +2,3x +2,…,3x +2的平均值为a,方差为b,
1 2 3 n
a=E(3X+2)=3E(X)+2=11,
b=D(3X+2)=9D(X)=9,
故选:BD.
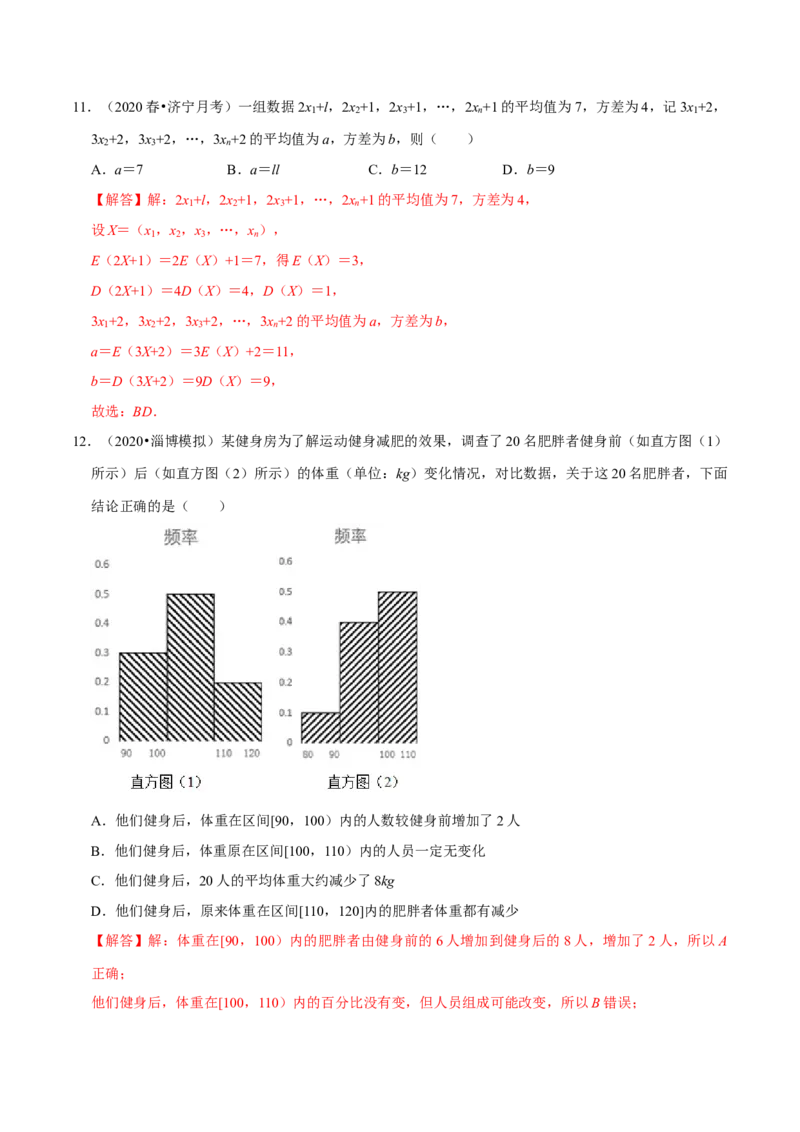
12.(2020•淄博模拟)某健身房为了解运动健身减肥的效果,调查了20名肥胖者健身前(如直方图(1)
所示)后(如直方图(2)所示)的体重(单位:kg)变化情况,对比数据,关于这20名肥胖者,下面
结论正确的是( )
A.他们健身后,体重在区间[90,100)内的人数较健身前增加了2人
B.他们健身后,体重原在区间[100,110)内的人员一定无变化
C.他们健身后,20人的平均体重大约减少了8kg
D.他们健身后,原来体重在区间[110,120]内的肥胖者体重都有减少
【解答】解:体重在[90,100)内的肥胖者由健身前的6人增加到健身后的8人,增加了2人,所以A
正确;
他们健身后,体重在[100,110)内的百分比没有变,但人员组成可能改变,所以B错误;他们健身后,20人的平均体重大约减少了
(0.3×95+0.5×105+0.2×115)﹣(0.1×85+0.4×95+0.5×105)=5(kg),所以C错误;
因为图(2)中没有体重在[110,120)内的人员,所以原来体重在[110,120)内的肥胖者体重都有减少,
所以D正确.
故选:AD.
三.填空题(共4小题)
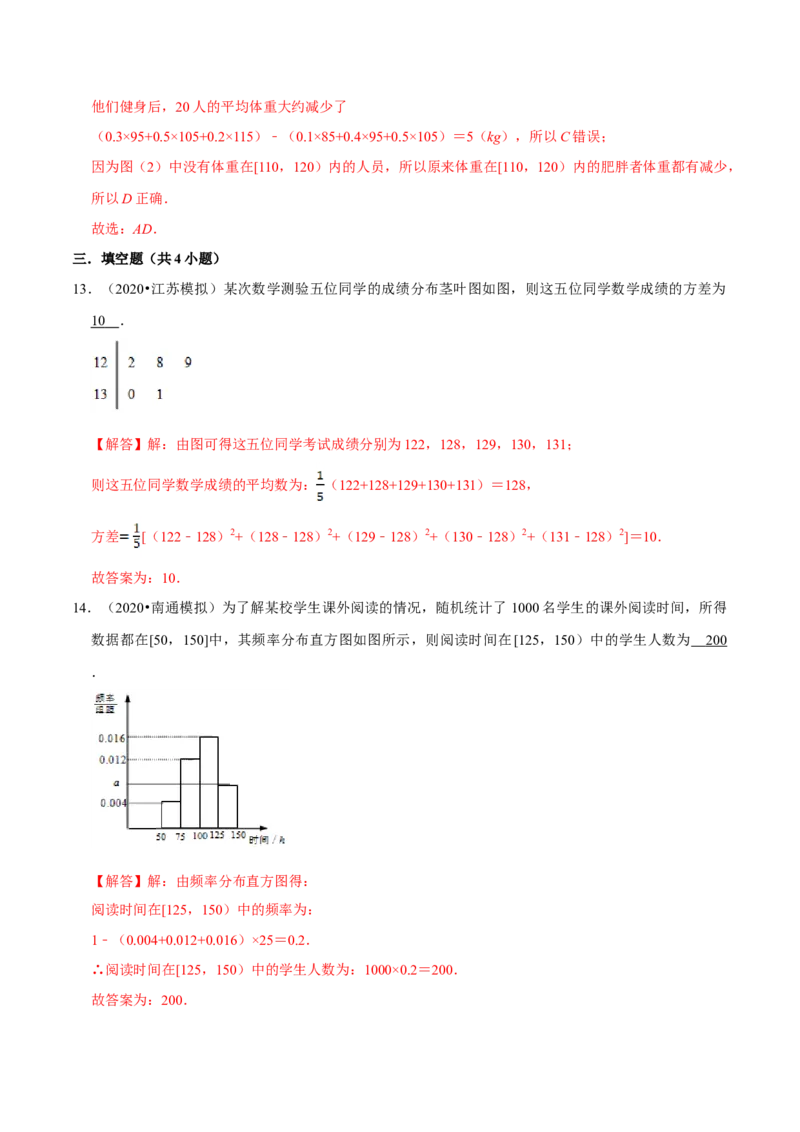
13.(2020•江苏模拟)某次数学测验五位同学的成绩分布茎叶图如图,则这五位同学数学成绩的方差为
10 .
【解答】解:由图可得这五位同学考试成绩分别为122,128,129,130,131;
则这五位同学数学成绩的平均数为: (122+128+129+130+131)=128,
方差 [(122﹣128)2+(128﹣128)2+(129﹣128)2+(130﹣128)2+(131﹣128)2]=10.
故答案为:10.
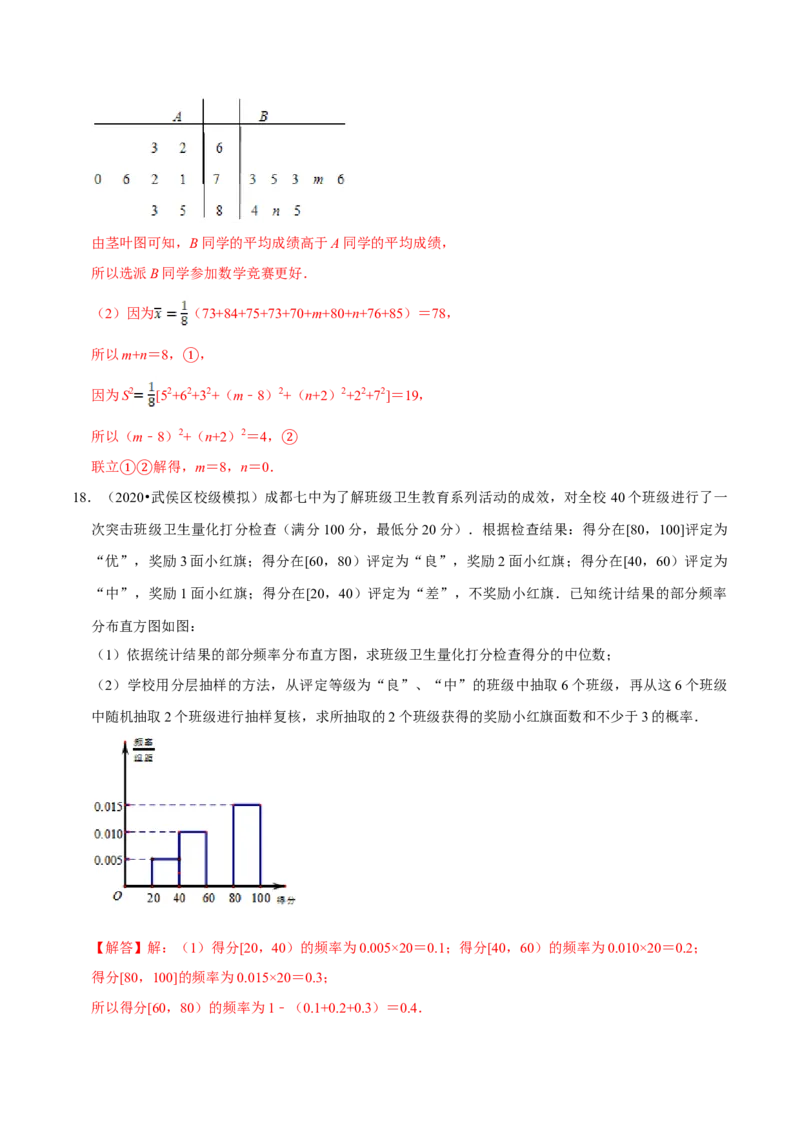
14.(2020•南通模拟)为了解某校学生课外阅读的情况,随机统计了 1000名学生的课外阅读时间,所得
数据都在[50,150]中,其频率分布直方图如图所示,则阅读时间在[125,150)中的学生人数为 200
.
【解答】解:由频率分布直方图得:
阅读时间在[125,150)中的频率为:
1﹣(0.004+0.012+0.016)×25=0.2.
∴阅读时间在[125,150)中的学生人数为:1000×0.2=200.
故答案为:200.15.(2020•扬州模拟)某校在高一、高二、高三三个年级中招募志愿者 50人,现用分层抽样的方法分配
三个年级的志愿者人数,已知高一、高二、高三年级的学生人数之比为4:3:3,则应从高三年级抽取
15 名志愿者.
【解答】解:∵高三年级的学生人数占的比例为 ,
则应从高三年级抽取的人数为50 15,
故答案为:15.
16.(2020•中卫三模)从2021个学生中选取202人志愿者,若采用下面的方法选取,先用简单随机抽样
法从2021人中剔除1人,剩下的2020人按系统抽样取出202人,则每人入选的概率 .
【解答】解:根据抽样的性质可知,无论哪种抽样,每个个体抽到的概率都是相同的,
用简单随机抽样从2021人中剔除1人,每个人被剔除的概率相等,
剩下的2020人再按系统抽样的方法抽取,每个人被抽取的概率也相等,即 ,
故答案为: .
四.解答题(共5小题)
17.(2020•宁德模拟)A、B两同学参加数学竞赛培训,在培训期间,他们参加了 8次测验,成绩(单位:
分)记录如下:
A 71 62 72 76 63 70 85 83
B 73 84 75 73 7 8 76 85
B同学的成绩不慎被墨迹污染( , 分别用m,n表示).
(1)用茎叶图表示这两组数据,现从A、B两同学中选派一人去参加数学竞赛,你认为选派谁更好?请
说明理由(不用计算);
(2)若B同学的平均分为78,方差s2=19,求m,n.
【解答】解:(1)A、B两同学参加了8次测验,成绩(单位:分)茎叶图如下:由茎叶图可知,B同学的平均成绩高于A同学的平均成绩,
所以选派B同学参加数学竞赛更好.
(2)因为 (73+84+75+73+70+m+80+n+76+85)=78,
所以m+n=8, ,
①
因为S2 [52+62+32+(m﹣8)2+(n+2)2+22+72]=19,
所以(m﹣8)2+(n+2)2=4,
联立 解得,m=8,n=0.②
18.(2①02②0•武侯区校级模拟)成都七中为了解班级卫生教育系列活动的成效,对全校 40个班级进行了一
次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果:得分在[80,100]评定为
“优”,奖励3面小红旗;得分在[60,80)评定为“良”,奖励2面小红旗;得分在[40,60)评定为
“中”,奖励1面小红旗;得分在[20,40)评定为“差”,不奖励小红旗.已知统计结果的部分频率
分布直方图如图:
(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数;
(2)学校用分层抽样的方法,从评定等级为“良”、“中”的班级中抽取6个班级,再从这6个班级
中随机抽取2个班级进行抽样复核,求所抽取的2个班级获得的奖励小红旗面数和不少于3的概率.
【解答】解:(1)得分[20,40)的频率为0.005×20=0.1;得分[40,60)的频率为0.010×20=0.2;
得分[80,100]的频率为0.015×20=0.3;
所以得分[60,80)的频率为1﹣(0.1+0.2+0.3)=0.4.设班级得分的中位数为x分,于是 ,解得x=70.
所以班级卫生量化打分检查得分的中位数为70分.
(2)由(1)知题意“良”、“中”的频率分别为0.4,0.2.又班级总数为40.
于是“良”、“中”的班级个数分别为16,8.
分层抽样的方法抽取的“良”、“中”的班级个数分别为4,2.
因为评定为“良”,奖励2面小红旗,评定为“中”,奖励1面小红旗.
所以抽取的2个班级获得的奖励小红旗面数和不少于3为两个评定为“良”的班级或一个评定为“良”
与一个评定为“中”的班级.
记这个事件为A.
则 为两个评定为“中”的班级.
把4个评定为“良”的班级标记为1,2,3,4,2个评定为“中”的班级标记为5,6.
从这6个班级中随机抽取2个班级用点(i,j)表示,其中1≤i<j≤6.
这些点恰好为6×6方格格点上半部分(不含i=j对角线上的点),于是有 种.
事件 仅有(5,6)一个基本事件.所以 .
所抽取的2个班级获得的奖励小红旗面数和不少于3的概率为 .
19.(2020•甲卷三模)中国女排一直是国人的骄傲,2019年女排世界杯于9月14日﹣9月29日在日本举
行,中国女排10连胜提前夺冠,获世界杯第五冠、三大赛第十冠.中国女排用胜利点燃国人的激情,
女排精神成为了拼搏、不服输的代表.某校受此影响,也举办了校园排球联赛,每班各自选出 12人代
表队,最后甲、乙两班进入决赛,如下茎叶图所示的是对每名队员上场时间做的统计,根据茎叶图回答
问题:
(Ⅰ)计算甲、乙两班队员上场的平均时间,并根据茎叶图分析哪班队员上场时间更均衡(不需要计
算);
(Ⅱ)赛后学校在上场时间超过50分钟(包括50分钟)的队员中随机抽取2人评为最佳运动员,则两
人中至少有一人来自乙班的概率是多少?【解答】解:(Ⅰ)甲班队员上场的平均时间
31.25,
乙班队员上场的平均时间 34.5.
由茎叶图分析甲班队员上场时间更均衡.
(Ⅱ)上场时间超过50分钟的队员甲班有两人为A,B,乙班有3人为C,D,E.
则从5人中随机抽取2人的取法有:AB,AC,AD,AE,BC,BD,BE,CD,CE,DE.共有10种,至
少有一人来自乙班的有9种,
故两人中至少有一人来自乙班的概率P .
20.(2020春•锡山区校级期中)为了落实习主席提出“绿水青山就是金山银山”的环境治理要求,某市
政府积极鼓励居民节约用水.计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准 x
(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用
水情况,通过抽样,获得了某年200位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,
2),…,[8,9)分成9组,制成了如图所示的频率分布直方图,其中0.4a=b.
(1)求直方图中a,b的值,并由频率分布直方图估计该市居民用水的平均数(每组数据用该组区间中
点值作为代表);
(2)设该市有40万居民,估计全市居民中月均用水量不低于2吨的人数,并说明理由;
(3)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.【解答】解:(1)由题意得: ,
解得a=0.15,b=0.06.
由频率分布直方图估计该市居民用水的平均数为:
0.5×0.04+1.5×0.08+2.5×0.15+3.5×0.20+4.5×0.26+5.5×0.15+6.5×0.06+7.5×0.04+8.5×0.02≈4.07.
(2)由频率分布直方图得:
全市居民中月均用水量不低于2吨的频率为:1﹣0.04﹣0.08=0.88,
∴全市居民中月均用水量不低于2吨的人数为:
400000×(1﹣0.04﹣0.08)=352000.
(3)∵前6组的频率之和是0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85,
而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85,
∴5≤x<6,
由0.15×(x﹣5)=0.85﹣0.73,解得:x=5.8,
因此,估计月用水量标准为5.8吨时,85%的居民每月的用水量不超过标准.
21.(2020•迎泽区校级模拟)2019年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实
行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善垃圾资源环境,某部门在某小
区年龄处于[20,45]岁的人中随机地抽取x人,进行了“垃圾分类”相关知识掌握和实施情况的调查,
并把达到“垃圾分类”标准的人称为“环保族”,得到如图示各年龄段人数的频率分布直方图和表中的
统计数据.
(1)求x,y,z的值;
(2)根据频率分布直方图,估计这x人年龄的平均值(同一组数据用该区间的中点值代替,结果按四
舍五入保留整数);
(3)从年龄段在[25,35]的“环保族”中采取分层抽样的方法抽取9人进行专访,并在这9人中选取2
人作为记录员,求选取的2名记录员中至少有一人年龄在[30,35]中的概率.
组数 分组 “环保族”人数 占本组频率
第一组 [20,25) 45 0.75
第二组 [25,30) 25 y
第三组 [30,35) 20 0.5
第四组 [35,40) z 0.2
第五组 [40,45) 3 0.1【解答】解:(1)由题意得: .
(2)根据频率分布直方图,估计这x人年龄的平均值为:
22.5×0.06×5+27.5×0.04×5+32.5×0.04×5+37.5×0.03×5+42.5×0.03×5=30.75≈31..
(3)从年龄段在[25,35]的“环保族”中采取分层抽样的方法抽取9人进行专访,
[25,30)中选:9 5人,[30,35]中选:9 4人,
在这9人中选取2人作为记录员,
基本事件总数n ,
选取的2名记录员中至少有一人年龄在[30,35]包含的基本事件个数:
m 26,
∴选取的2名记录员中至少有一人年龄在[30,35]中的概率p .