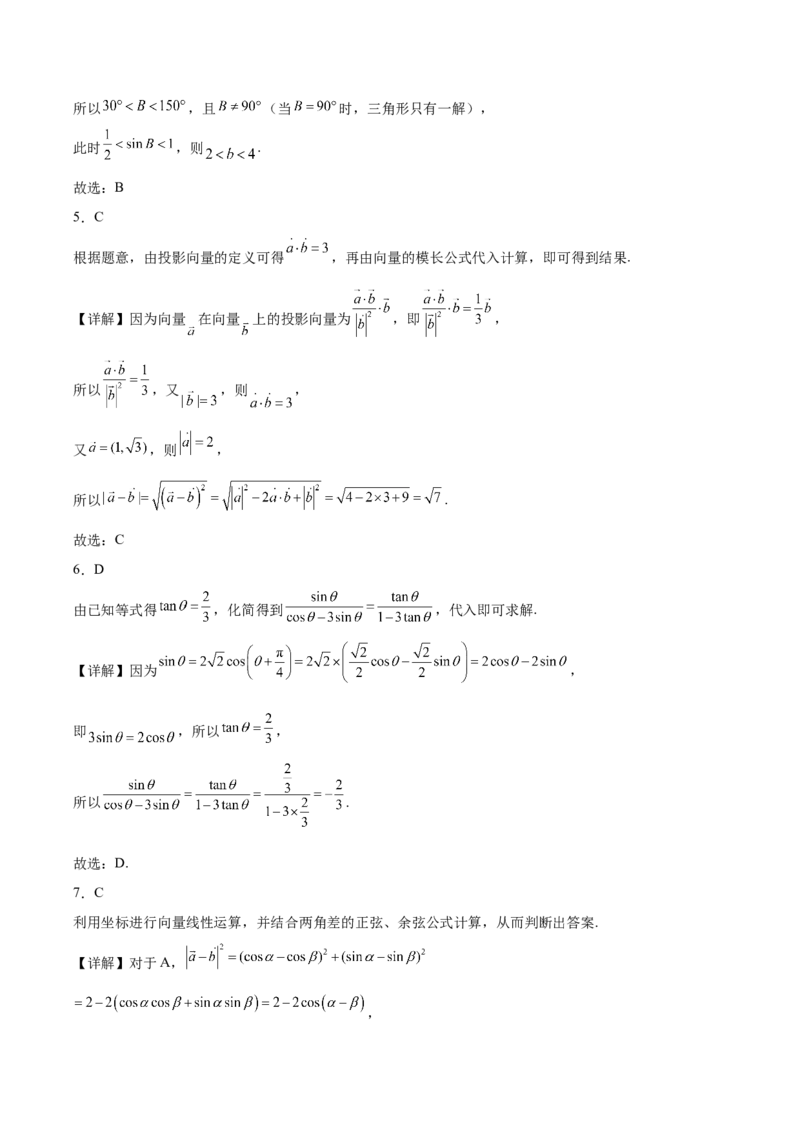文档内容
2024-2025学年高一下学期期中质量检测数学试卷
一、单选题
1.
A. B. C. D.
2.在 中,角A,B,C的对边分别为a,b,c,若 , , ,则 ( )
A. B.1 C. D.
3.已知三点 ,若 和 是相反向量,则D点坐标为( )
A. B. C. D.
4.在 中,角A,B,C的对边分别为a,b,c.已知 ,若满足条件的 有两个,则
b的取值范围是( )
A. B. C. D.
5.已知向量 ,且向量 在向量 上的投影向量为 ,则 ( )
A.1 B.2 C. D.
6.已知 ,则 ( )
A. B. C. D.
7.已知 ,向量 ,则下列可能成立的是( )
A. B. C. D.
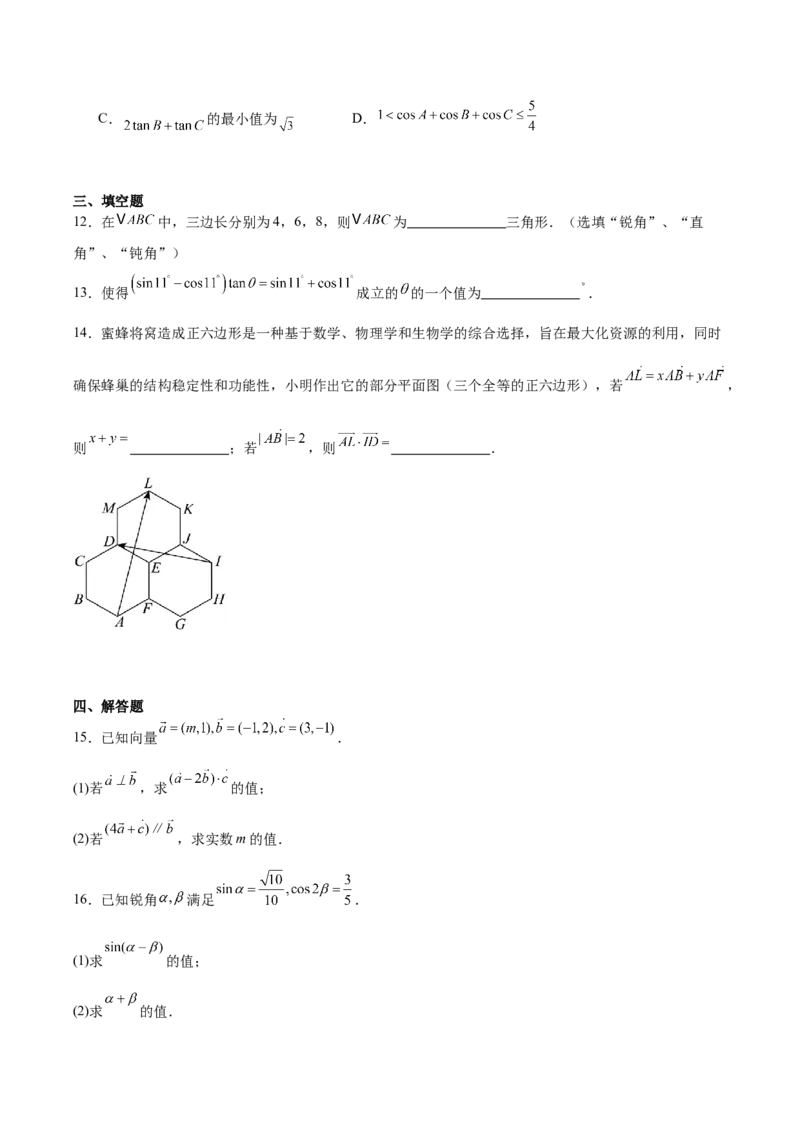
8.密铺,即平面图形的镶嵌,用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留
空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌.皇冠图形(图1)是一个密铺图形,它由四个完全相同的平面凹四边形组成.在平面凹四边形 (图2)中,测得
,凹四边形 的面积为 ,则 的余弦值为( )
A. B. C. D.
二、多选题
9.已知非零向量 ,则下列说法正确的是( )
A.若 ,则向量 夹角为锐角
B.若 ,则
C.若 ,则 与 的夹角是
D.若 ,则
10.已知 ,则( )
A. B.
C. D.
11.在斜三角形 中,角A,B,C的对边分别为a,b,c.若 ,则( )
A. 为锐角三角形 B.若 ,则C. 的最小值为 D.
三、填空题
12.在 中,三边长分别为4,6,8,则 为 三角形.(选填“锐角”、“直
角”、“钝角”)
13.使得 成立的 的一个值为 .
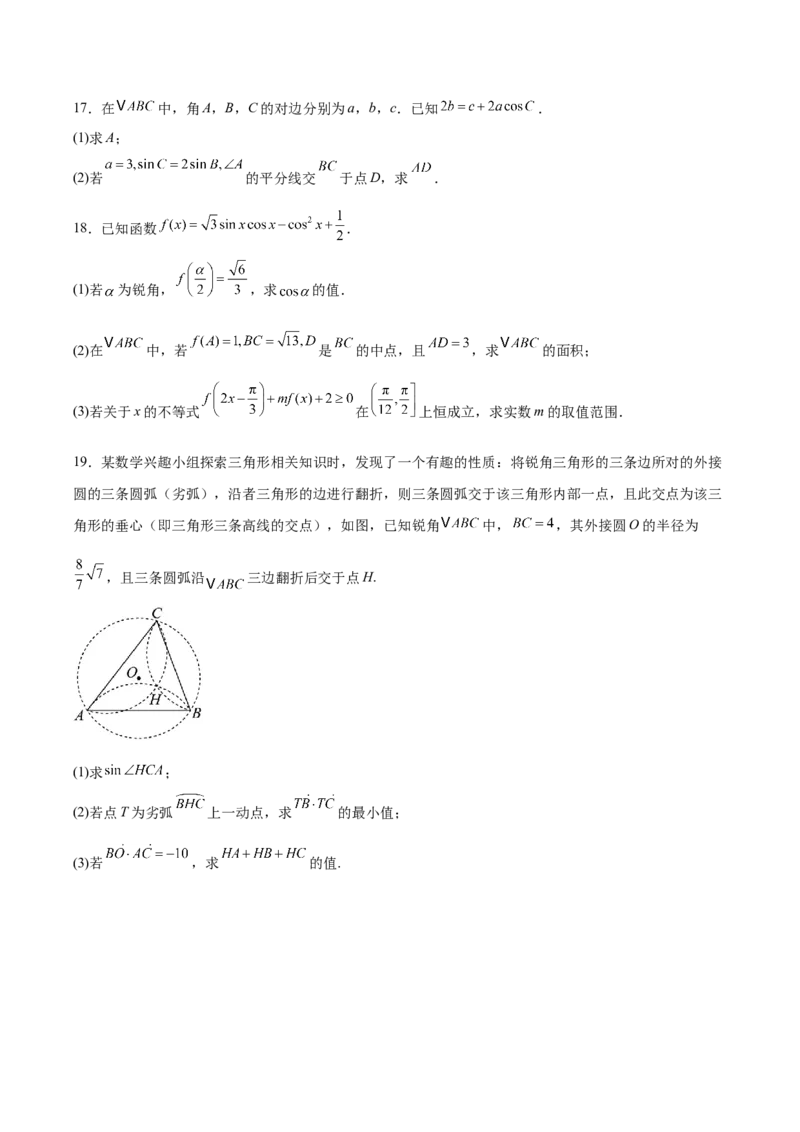
14.蜜蜂将窝造成正六边形是一种基于数学、物理学和生物学的综合选择,旨在最大化资源的利用,同时
确保蜂巢的结构稳定性和功能性,小明作出它的部分平面图(三个全等的正六边形),若 ,
则 ;若 ,则 .
四、解答题
15.已知向量 .
(1)若 ,求 的值;
(2)若 ,求实数m的值.
16.已知锐角 满足 .
(1)求 的值;
(2)求 的值.17.在 中,角A,B,C的对边分别为a,b,c.已知 .
(1)求A;
(2)若 的平分线交 于点D,求 .
18.已知函数 .
(1)若 为锐角, ,求 的值.
(2)在 中,若 是 的中点,且 ,求 的面积;
(3)若关于x的不等式 在 上恒成立,求实数m的取值范围.
19.某数学兴趣小组探索三角形相关知识时,发现了一个有趣的性质:将锐角三角形的三条边所对的外接
圆的三条圆弧(劣弧),沿者三角形的边进行翻折,则三条圆弧交于该三角形内部一点,且此交点为该三
角形的垂心(即三角形三条高线的交点),如图,已知锐角 中, ,其外接圆O的半径为
,且三条圆弧沿 三边翻折后交于点H.
(1)求 ;
(2)若点T为劣弧 上一动点,求 的最小值;
(3)若 ,求 的值.题号 1 2 3 4 5 6 7 8 9 10
答案 C C A B C D C A BCD AC
题号 11
答案 BCD
1.C
利用两角和差正弦公式化简求得结果.
【详解】 .
故选: .
2.C
【详解】在 中,∵ , ,
∴由三角形内角和定理可知: .
在 中,由正弦定理 可知: .
故选:C.
3.A
【详解】设 ,∵ ,
∴ , .
∵ 和 是相反向量,
∴ ,即 ,解得 .
故选:A.
4.B
由正弦定理可得 ,再由三角形有两解可得角 的范围,从而得到结果.
【详解】由正弦定理可得 ,则 ,
因为 ,且满足条件的 有两个,所以 ,且 (当 时,三角形只有一解),
此时 ,则 .
故选:B
5.C
根据题意,由投影向量的定义可得 ,再由向量的模长公式代入计算,即可得到结果.
【详解】因为向量 在向量 上的投影向量为 ,即 ,
所以 ,又 ,则 ,
又 ,则 ,
所以 .
故选:C
6.D
由已知等式得 ,化简得到 ,代入即可求解.
【详解】因为 ,
即 ,所以 ,
所以 .
故选:D.
7.C
利用坐标进行向量线性运算,并结合两角差的正弦、余弦公式计算,从而判断出答案.
【详解】对于A,
,因为 ,所以 ,
,则 ,则 ,
故A错误;
对于B,因为 ,
因为 ,所以 ,
则 ,所以 不成立,故B错误;
对于C,因为 ,
因为 ,所以 ,
所以 ,则有可能 ,
所以 可能成立,故C正确;
对于D,
,
因为 ,所以 ,
所以 , 则 ,
所以 ,
, ,
则 ,所以 ,故D错误.
故选:C.
8.A
在图2中连接 ,在 和 中,分别利用余弦定理可得 ,利用三角形的面积公式可得 ,两式平方相加,由两角差的余弦
公式,即可求出 的余弦值.
【详解】如图,连接 ,
因为 ,
在 中,由余弦定理得 ,
则 ,
在 中,由余弦定理得 ,
则 ,
所以 ,
即 ,①
因为 ,
,
所以 ,②
则①式和②式分别平方并相加得:
,
则 ,所以 ,
即 的余弦值为 .
故选:A.
9.BCD
对于A,因为 时,向量的夹角为锐角或零度角,即可判断;对于B,由 与 表示同向的单位向量,即可判断;对于C,利用向量的线性运算知识结合图形,即可判断;对于D,由 ,设 ,
代入等式两边利用运算法则运算,即可判断.
【详解】向量 是非零向量,
对于A,因为 ,即 ,
所以向量 夹角为锐角或零度角,故A错误;
对于B,因为 ,所以 与 方向相同,
又 表示与 同向的单位向量, 表示与 同向的单位向量,
所以 ,故B正确;
对于C,设 , ,由向量线性运算知:
, ,如下图所示:
因为 ,
所以 与 均为等边三角形, ,
又四边形 为菱形,所以 ,
即 与 的夹角为 ,故C正确;
对于D,因为 ,设 ,
则 , ,所以 ,故D正确.
故选:BCD.
10.AC
将原式平方即可判断A,由 即可判断B,结合二倍角公式以及余弦的和差角
公式化简即可判断C,由 与 的值代入计算,即可判断D.
【详解】由 可得 ,则 ,故A正确;
且 ,则 ,
所以 ,
且 ,则 ,故B错误;
,故C正确;
因为 ,
由 , 可得 ,故D错误;
故选:AC
11.BCD
由诱导公式即可判断A,由正弦定理即可判断B,由条件可得 ,结合基本不
等式代入计算,即可判断C,由条件可得 ,然后换元,结合二
次函数的值域,即可判断D.
【详解】对于A,由 可得 ,则 或 ,即 或 ,
因为三角形 为斜三角形,若 ,则 , ,
不符合斜三角形,所以 ,即 为钝角, 为钝角三角形,故A错误;
对于B,由正弦定理可得 ,则 ,
所以 ,故B正确;
对于C,由 , 可得 ,
且 ,则 ,
则
,
当且仅当 时,即 时,等号成立,故C正确;
对于D,由C可知 , ,
则 ,
令 ,
由 可得 ,则 ,
所以 ,故 ,
且 ,所以 ,
当 时,取得最大值 ,
当 或 时,最小值为 ,
所以 ,故D正确;
故选:BCD
12.钝角
设边长为8的边对应的角为 ,利用余弦定理可判断.
【详解】设边长为8的边对应的角为 ,
由余弦定理可得 ,
所以 为钝角,因此,三角形为钝角三角形,
故答案为:钝角.
13. (答案不唯一,满足 即可)
根据题中条件将式子变形为 ,分子、分母同时除以 将弦化切,然后利用
及两角和的正切公式、诱导公式即可求解.
【详解】∵ ,
∴
,
∴ .
故答案为: (答案不唯一,满足 即可).
14.
结合正六边形的性质以及平面向量的线性运算即可得到结果;再将 分别用 表示出来,结合向量数量积的运算律代入计算,即可得到结果.
【详解】观察图形可知, 三点共线,且 ,
因为 ,
且 ,
则 ,
所以 ,即 ;
由正六边形的性质可得
,
所以
.
故答案为: ;
15.(1)
(2)
(1)由向量垂直的坐标运算可得 的值,然后代入计算,即可得到结果;
(2)先表示出 的坐标,再由向量平行的坐标运算代入计算,即可得到结果.
【详解】(1)由 可得 ,即 ,解得 ,所以 ,
则 ,
所以 .(2)因为 ,
由 可得 ,解得 .
16.(1)
(2)
(1)由题意求出 ,利用两角差的正弦公式即可求得 ;
(2)由(1)解出 ,由 均为锐角以及 的取值情况,解出 的取值范围,
即可求得 的值.
【详解】(1)因为 , ,所以 ,
因为 , ,所以 ,
则 ,又 ,所以 ,则 ,
所以 .
(2)由(1)得 ,
因为 , , ,所以 ,
由(1)知 ,所以 ,
则 ,所以 .17.(1)
(2)
(1)根据题意,由正弦定理的边角互化代入计算,即可得到结果;
(2)先由余弦定理可得 的值,再由等面积法结合三角形的面积公式代入计算,即可得到结果.
【详解】(1)由正弦定理可得 ,
即 ,
,
即 ,且 ,
则 , ,则 .
(2)由 可得 ,
由正弦定理可得 ,
即 ,解得 ,则 ,
且 为角 的角平分线,
,即 ,
化简可得 ,解得 .
18.(1)
(2)
(3)
(1)由恒等变换公式化简函数解析式,即可得到 ,再由 代入计算,即
可得到结果;(2)由中线可得 ,从而可得 ,结合余弦定理与三角形的面积公式代入计
算,即可得到结果;
(3)将不等式化简,然后换元可得 在 上恒成立,分离参数结合基本不等式代入计算,
即可得到结果.
【详解】(1) ,
由 可得 ,
且 为锐角,则 ,即 ,则 ,
即 ,
所以
.
(2)因为 ,且 ,则 ,
则 ,解得 ,
由 为三角形的中线,则 ,
即 ,
即 ,化简可得 ①,
由余弦定理可得 ,化简可得 ②,
① ②可得 ,即 ,
则 .
(3) ,
由 可得 ,则 ,
由不等式 在 上恒成立,
可得 在 上恒成立,
且
,
令 ,则 ,
则不等式 在 上恒成立,
即 在 上恒成立,
又 ,当且仅当 时,即 时等号成立,
所以 ,即 ,
则实数m的取值范围是 .19.(1)
(2)
(3)
(1)在锐角 中,由正弦定理求出 ,利用同角三角函数的平方关系求出 .利用三
角形垂心性质可得 ,结合三角形诱导公式即可求解;
(2)设点M为 的边 所对的外接圆的劣弧,点D为边 的中点.
由题意及对称性可知 .故要使 取得最小值,只需 最小.分析可知当
三点共线 最小,即可求解.
(3)由向量减法运算可知 ,由圆的性质可知 , ,
从而 .由(1)可求 ,可求解 .在锐角 中,
由二倍角公式、三角形内角和定理、诱导公式及正弦定理可解 .由点H是 的垂心可得
, , .
在 中,由正弦定理可求得 ,同理可求 , ,本题即可求解.
【详解】(1)在锐角 中,∵ ,其外接圆O的半径为 ,
∴由正弦定理可得: ,解得 .
.
由题可知 , .
(2)设点M为 的边 所对的外接圆的劣弧,点D为边 的中点.
由题意及对称性可知 .故要使 取得最小值,只需 最小.
在圆 上,由三角形三边关系可知 ,当且仅当 三点共线时取等号,此时
.
∴ ,
即 的最小值为 .
(3)由(1)可知: , .
, .
又 ,
∴由圆的性质可知
.
又 ,
∴ ,解得 .
∴在锐角 中, , ,
,
.
∴由正弦定理可得: ,∴ , .
在 中,由点H是 的垂心可得 , , .
在 中,由正弦定理可得 ,
.
同理可得 ,
,