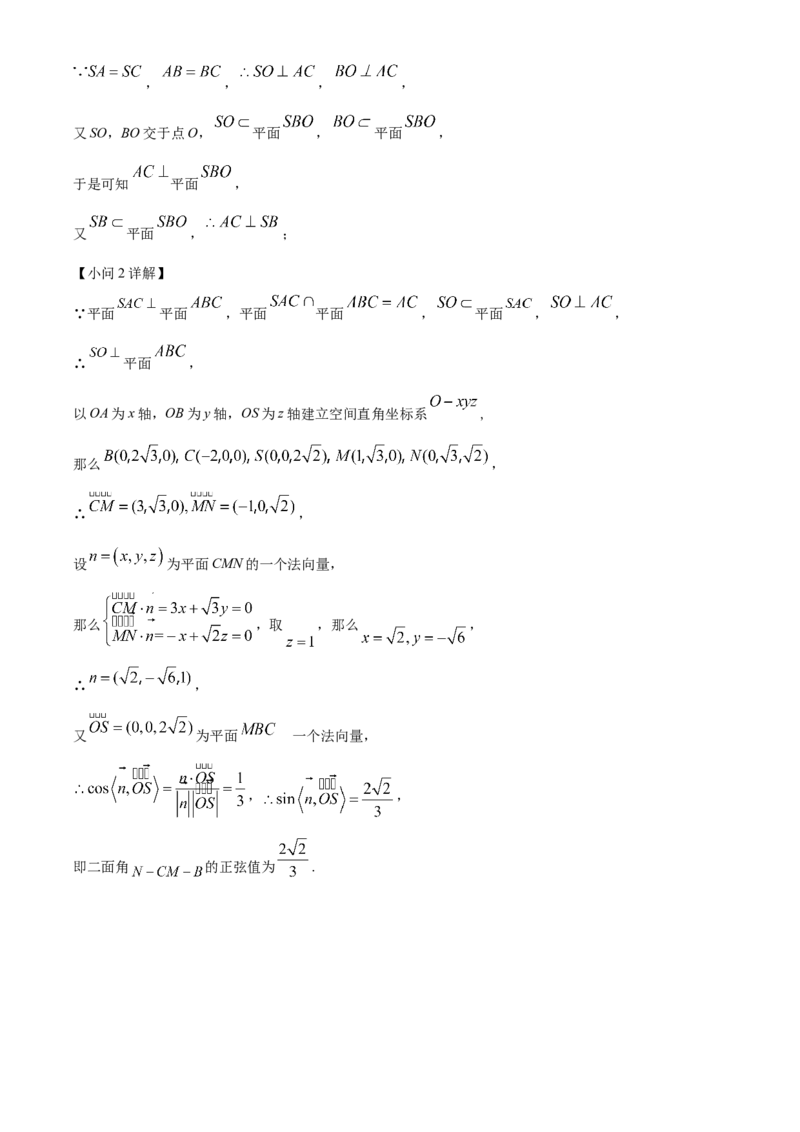文档内容
友好学校第七十六届期末联考
高三数学
说明:本试卷共22题,共4页.考试时间为120分钟,满分150分.
注意事项:
1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码粘贴到条形码区域内.
2选择题必须用2B铅笔填涂﹔非选择题必须用0.5mm黑色中性笔书写,字体工整,笔迹清楚.
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效,在草
纸、试题卷上答题无效.
4.保持卡面清洁,不要折叠,不要弄破、弄皱、不准使用涂改液、修正带、刮纸刀.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求.
1. 设集合 ,则 ( )
A. B. C. D.
2. 若复数 为纯虚数,则实数m的值为( )
A. 1 B. -1 C. 2 D. -2
3. 设函数 在 处的切线与直线 平行,则 ( )
A. B. 2 C. D. 1
4. 2023年7月28日、第31届世界大学生夏季运动会将在成都东安湖体育公园开幕.公园十二景中的第一
景东安阁,阁楼整体采用唐代风格、萃取太阳神乌形象、蜀锦与宝相花纹(芙蓉花)元素,严谨地按照唐
式高阁的建筑形制设计建造,已成为成都市文化新地标,面向世界展现千年巴蜀风韵.某数学兴趣小组在
探测东安阁高度的实践活动中,选取与阁底A在同一水平面的B,C两处作为观测点,测得 ,
, ,在C处测得阁顶 的仰角为45°,则他们测得东安阁的高度 为(精确
到 ,参考数据: , )( )A. B. C. D.
5. 已知等差数列 的前 项和为 .若 , ,则 ( )
A. B. C. D.
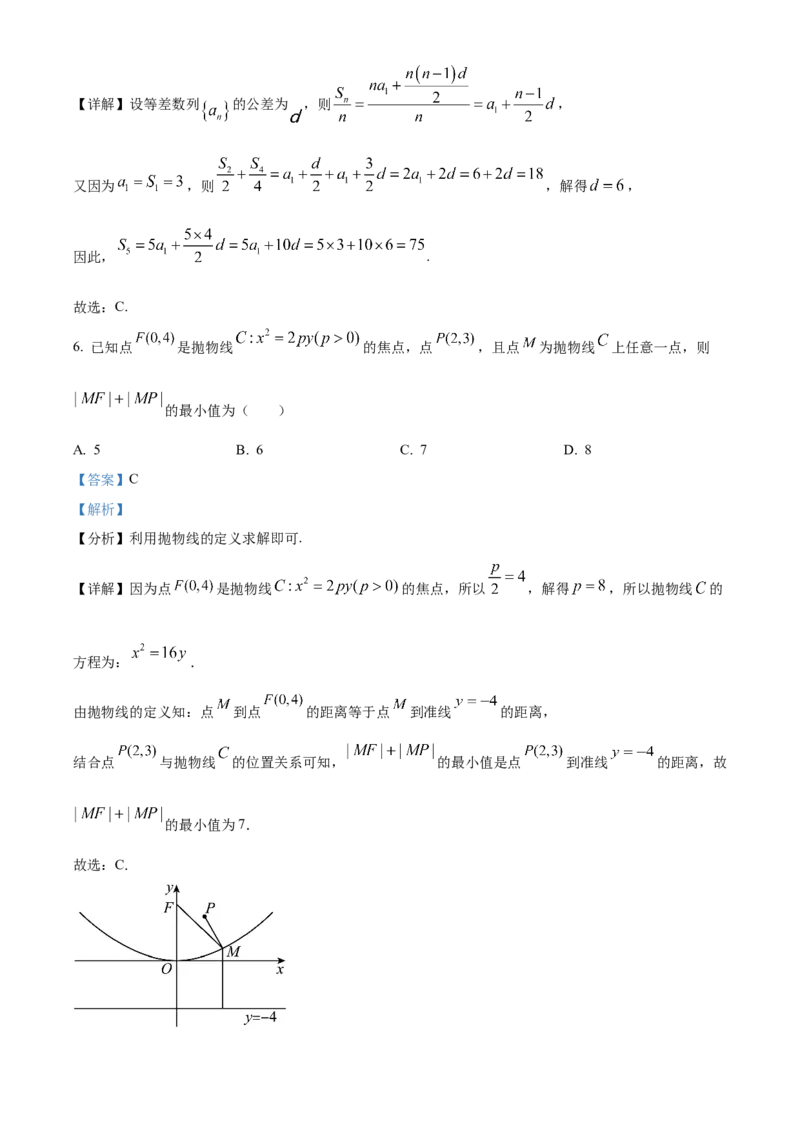
6. 已知点 是抛物线 的焦点,点 ,且点 为抛物线 上任意一点,则
的最小值为( )
A. 5 B. 6 C. 7 D. 8
7. 已知定义在 上的函数 , , , ,则a,b,
c的大小关系为( )
A. B.
C. D.
8. 已知三棱锥 的顶点都在球 的球面上, 平面 ,若球 的体
积为 ,则该三棱锥的体积的最大值是( )
A. B. 5 C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项
符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列命题中是真命题的是( )
A. “ ”是“ ”的充分不必要条件B. 命题“ , ” 的否定是“ : , ”
C. 把 的图像向左平移 个单位长度,得到的图像的解析式为
D.
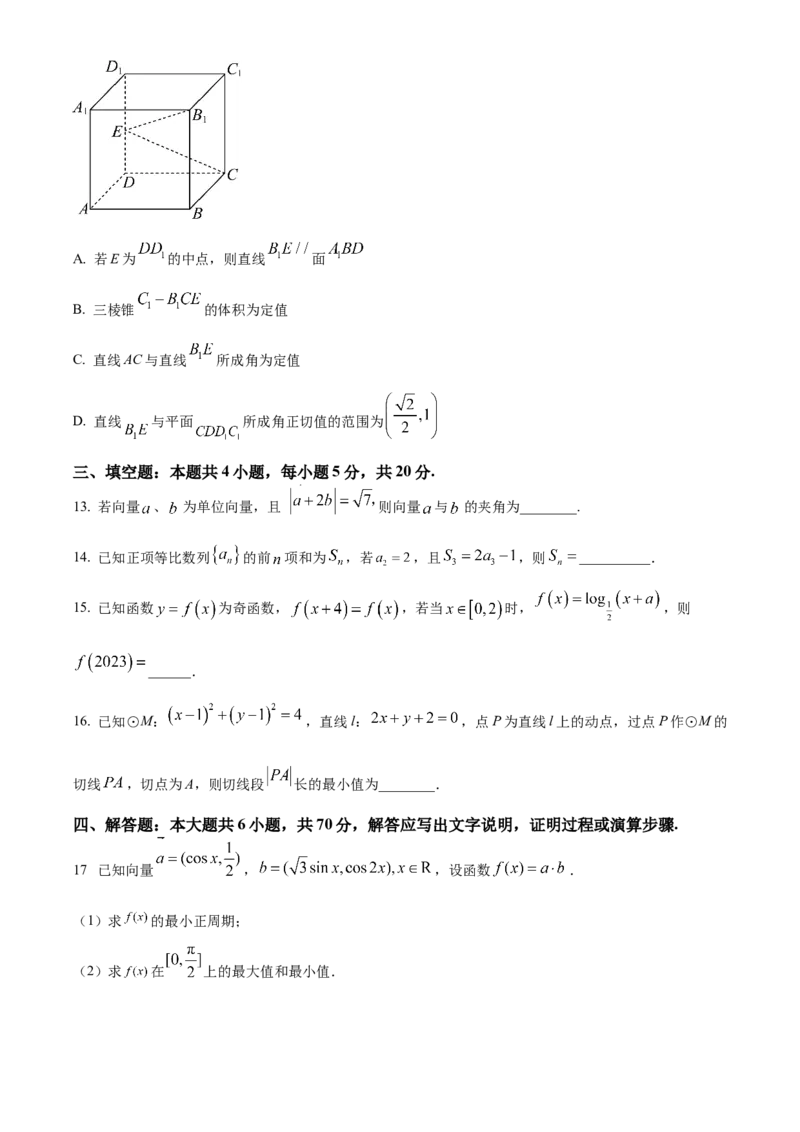
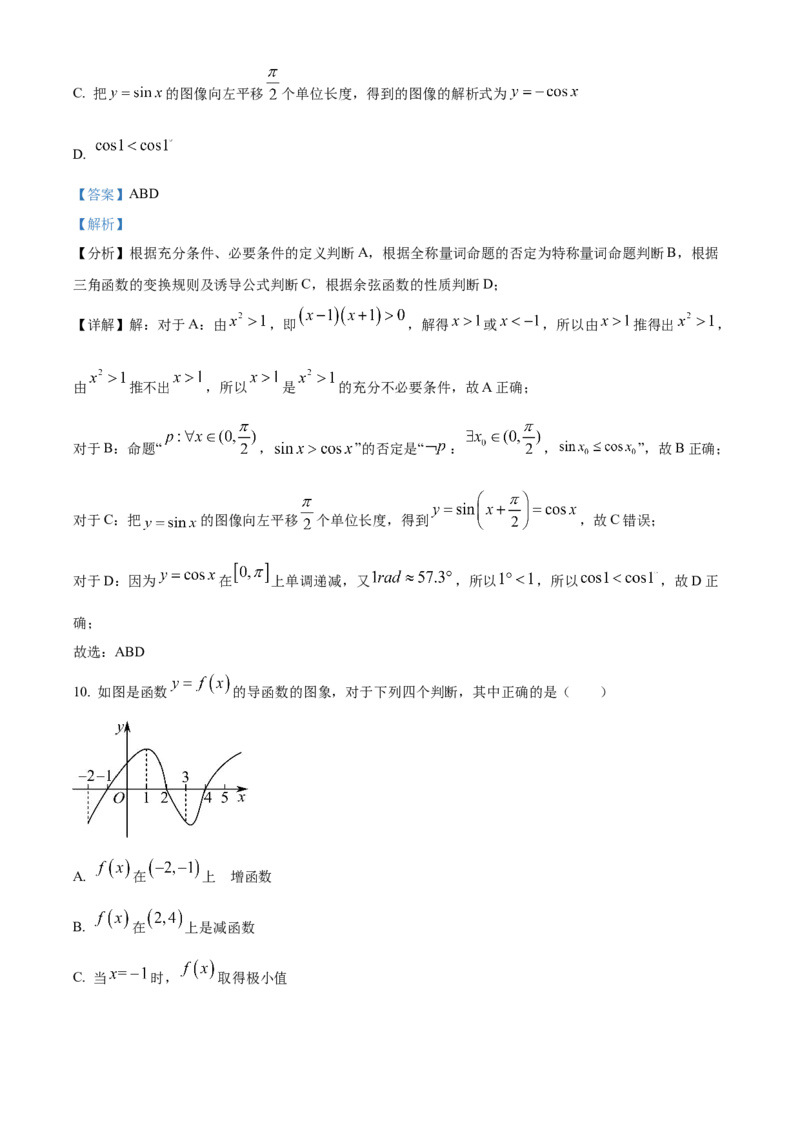
10. 如图是函数 的导函数的图象,对于下列四个判断,其中正确的是( )
A. 在 上 是增函数
B. 在 上是减函数
C. 当 时, 取得极小值
D. 当 时, 取得极大值
11. 已知双曲线 的左、右焦点分别为 ,抛物线 的焦点与双曲线C的
一个焦点重合,点P是这两条曲线的一个公共点,则下列说法正确的是( )
的
A. B. 周长为16
C. 的面积为 D.
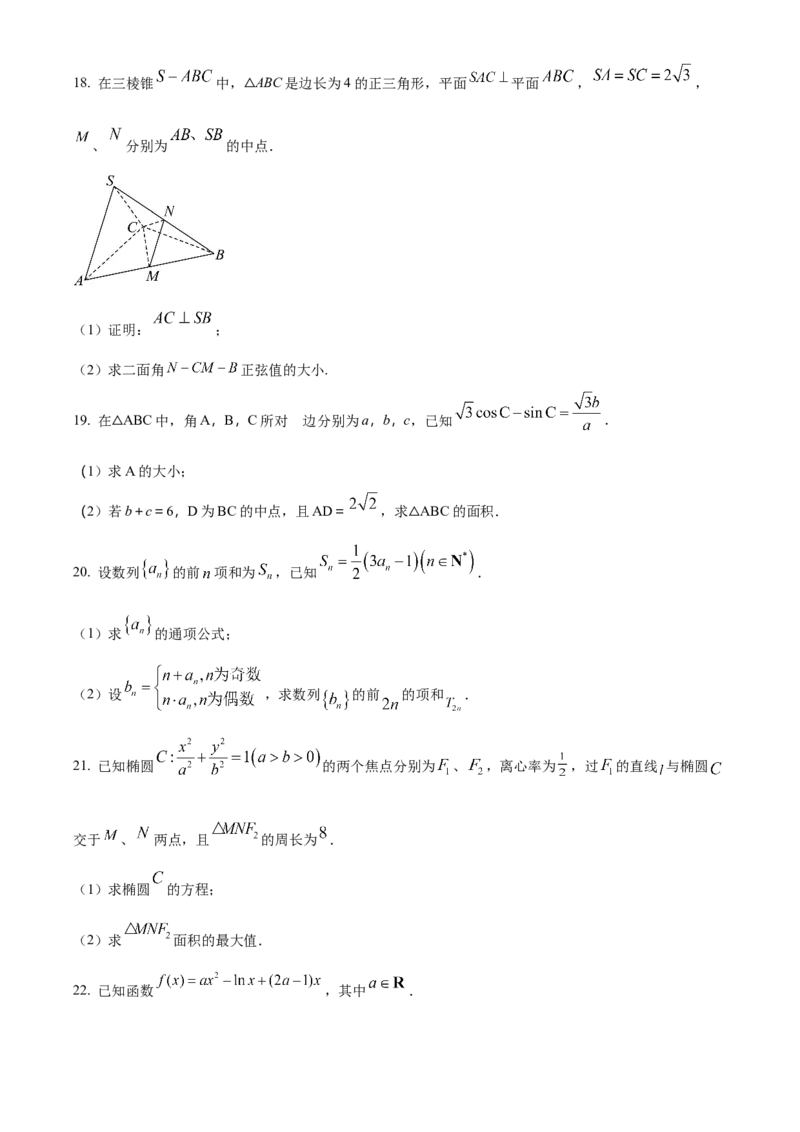
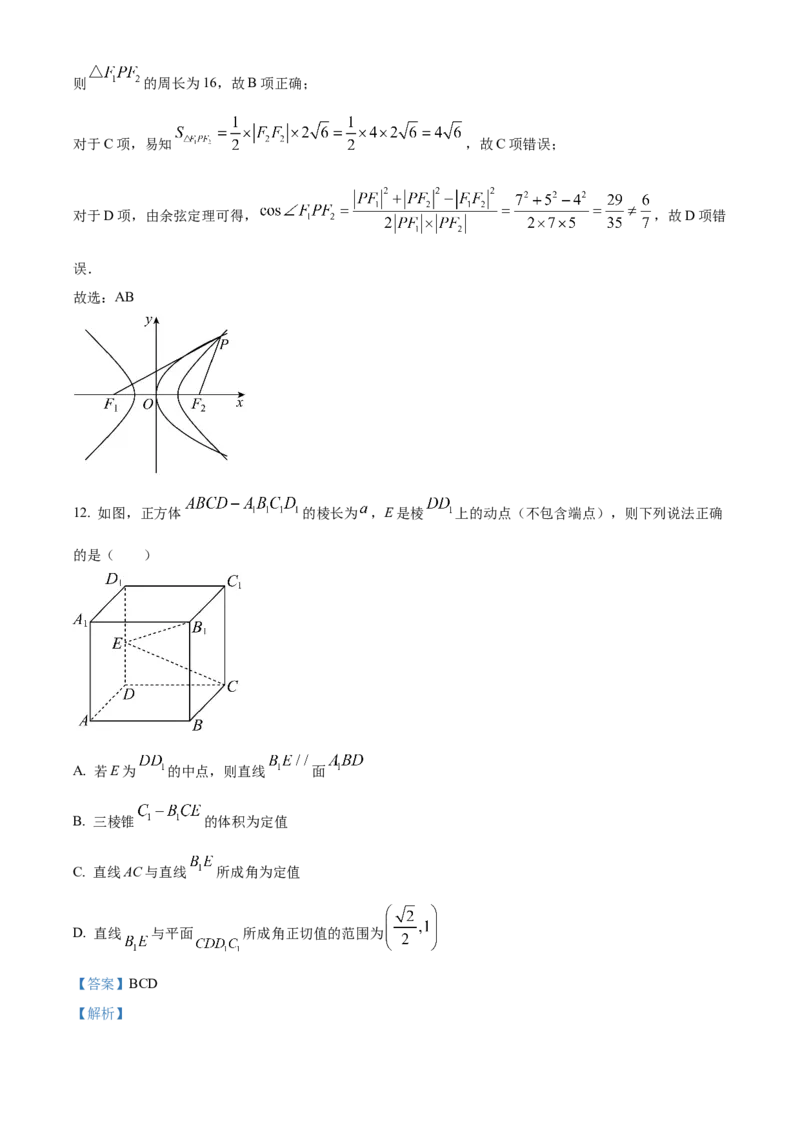
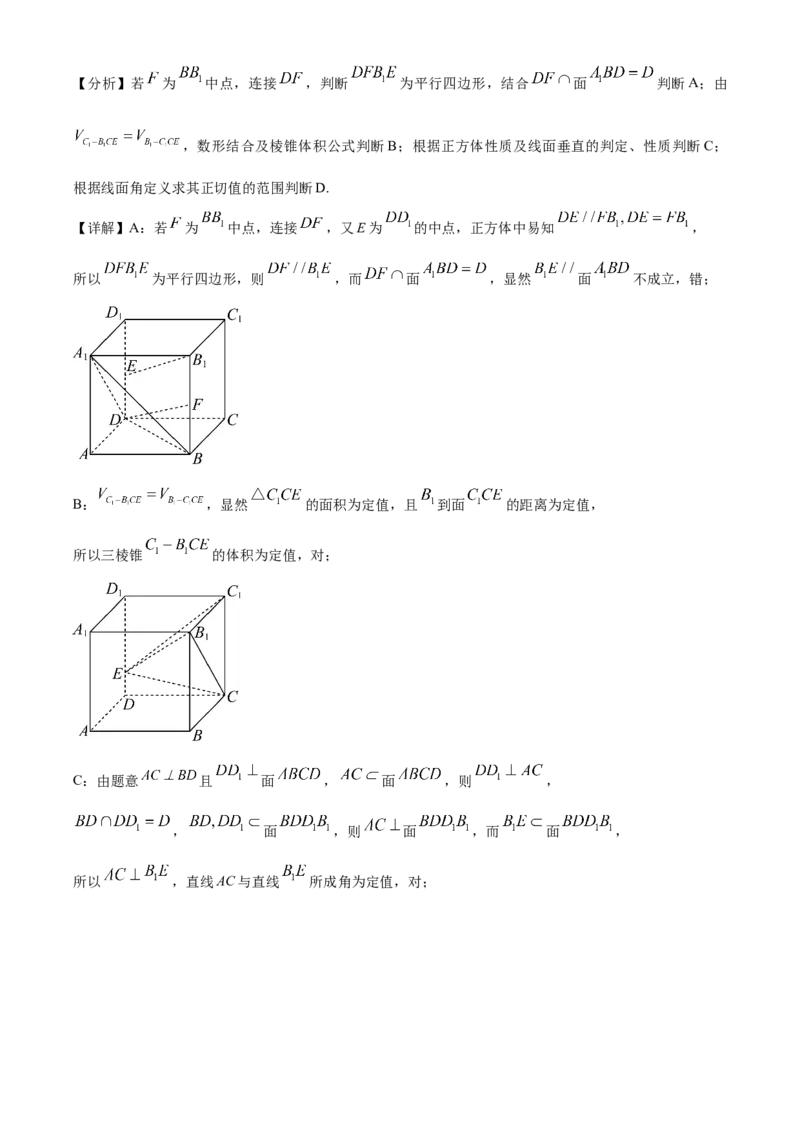
12. 如图,正方体 的棱长为 ,E是棱 上的动点(不包含端点),则下列说法正确
的是( )A. 若E为 的中点,则直线 面
B. 三棱锥 的体积为定值
C. 直线AC与直线 所成角为定值
D. 直线 与平面 所成角正切值的范围为
三、填空题:本题共4小题,每小题5分,共20分.
13. 若向量 、 为单位向量,且 则向量 与 的夹角为________.
14. 已知正项等比数列 的前 项和为 ,若 ,且 ,则 __________.
15. 已知函数 为奇函数, ,若当 时, ,则
______.
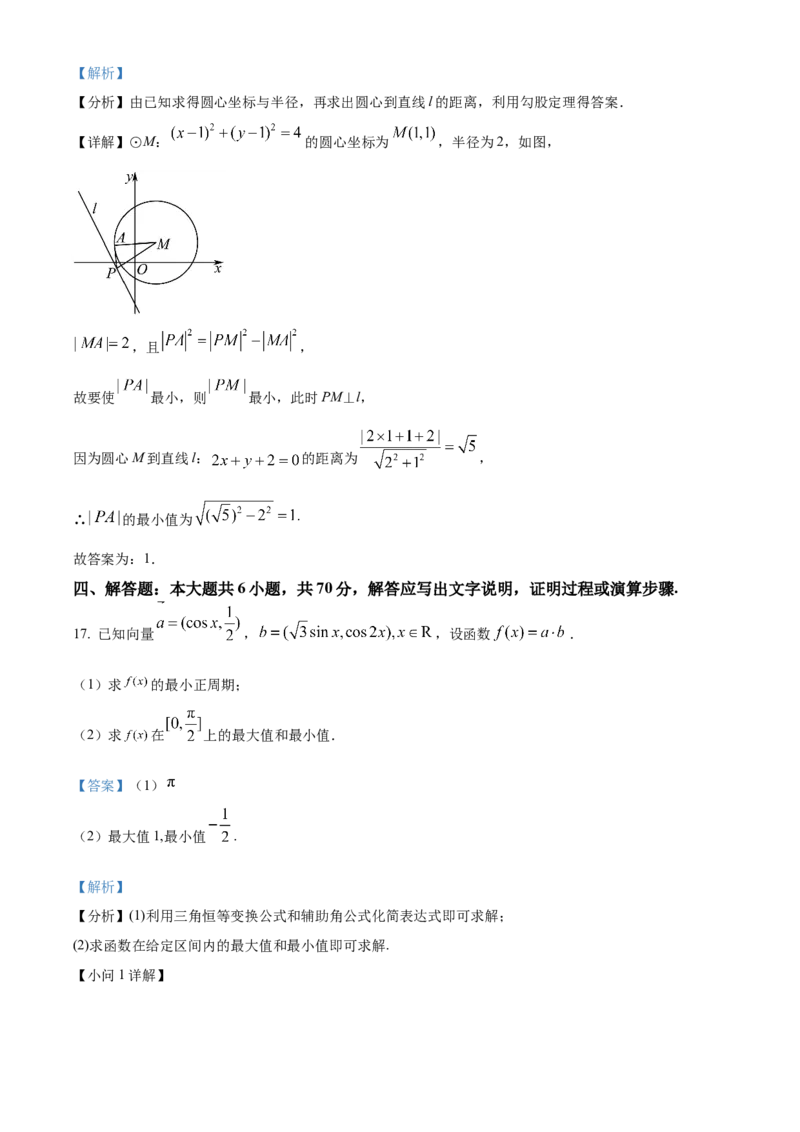
16. 已知⊙M: ,直线l: ,点P为直线l上的动点,过点P作⊙M的
切线 ,切点为A,则切线段 长的最小值为________.
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
.
17 已知向量 , ,设函数 .
(1)求 的最小正周期;
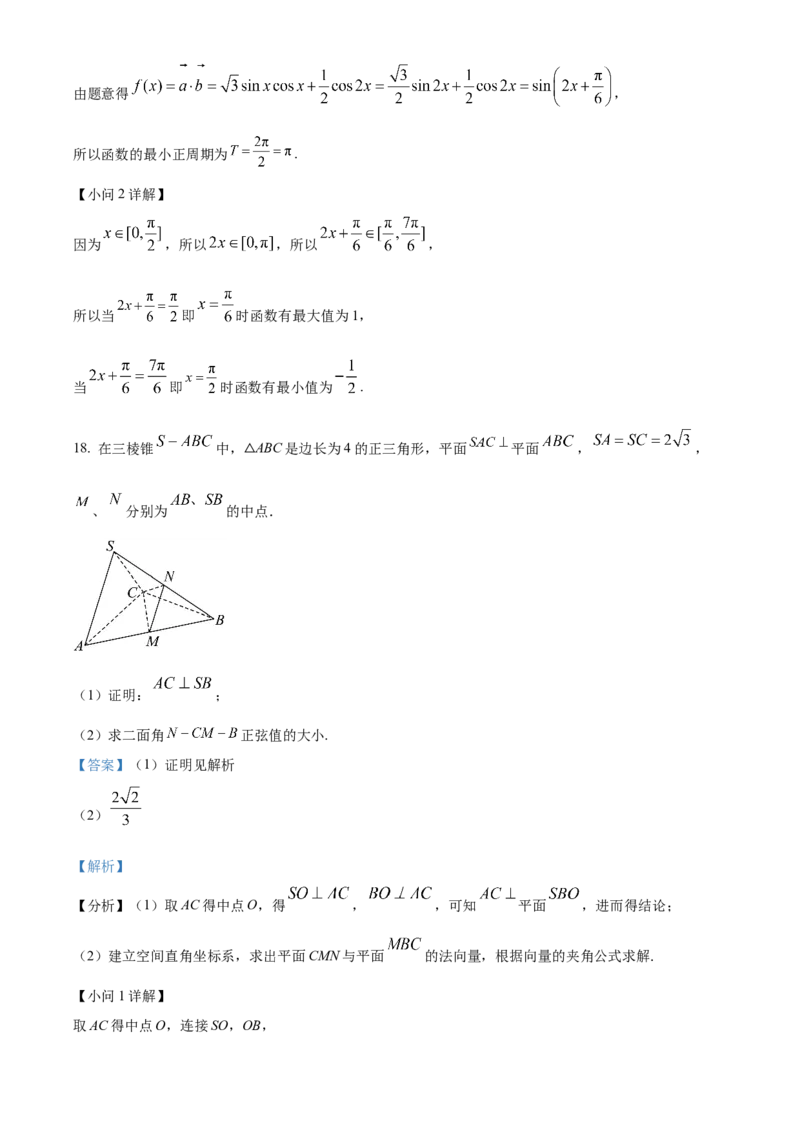
(2)求 在 上的最大值和最小值.18. 在三棱锥 中, ABC是边长为4的正三角形,平面 平面 , ,
△
、 分别为 的中点.
(1)证明: ;
(2)求二面角 正弦值的大小.
19. 在 ABC中,角A,B,C所对 的边分别为a,b,c,已知 .
△
(1)求A的大小;
(2)若b+c=6,D为BC的中点,且AD= ,求 ABC的面积.
△
20. 设数列 的前 项和为 ,已知 .
(1)求 的通项公式;
(2)设 ,求数列 的前 的项和 .
21. 已知椭圆 的两个焦点分别为 、 ,离心率为 ,过 的直线 与椭圆
交于 、 两点,且 的周长为 .
(1)求椭圆 的方程;
(2)求 面积的最大值.
22. 已知函数 ,其中 .(1)讨论 的单调性;
(2)设 ,若不等式 对 恒成立,求 的取值范围.友好学校第七十六届期末联考
高三数学
说明:本试卷共22题,共4页.考试时间为120分钟,满分150分.
注意事项:
1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码粘贴到条形码区域内.
2选择题必须用2B铅笔填涂﹔非选择题必须用0.5mm黑色中性笔书写,字体工整,笔迹清楚.
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效,在草
纸、试题卷上答题无效.
4.保持卡面清洁,不要折叠,不要弄破、弄皱、不准使用涂改液、修正带、刮纸刀.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求.
1. 设集合 ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】由描述法表示集合,求函数的定义域可得集合A,再由集合的交集的定义可求解.
【详解】集合 ,故 ,
故选:B.
2. 若复数 为纯虚数,则实数m的值为( )
A. 1 B. -1 C. 2 D. -2
【答案】D
【解析】
【分析】根据除法运算求出 ,再根据纯虚数的定义可得结果.
【详解】 ,
因为 为纯虚数,所以 ,得 .
故选:D3. 设函数 在 处的切线与直线 平行,则 ( )
.
A B. 2 C. D. 1
【答案】D
【解析】
【分析】由条件,根据导数的几何意义及两平行直线的斜率关系列方程求 .
【详解】函数 的定义域为 ,
由已知 ,故 ,
函数 的导函数 ,
所以 ,
因为函数 在 处的切线与直线 平行,
所以 ,所以 ,经验证,此时满足题意.
.
故选:D
4. 2023年7月28日、第31届世界大学生夏季运动会将在成都东安湖体育公园开幕.公园十二景中的第一
景东安阁,阁楼整体采用唐代风格、萃取太阳神乌形象、蜀锦与宝相花纹(芙蓉花)元素,严谨地按照唐
式高阁的建筑形制设计建造,已成为成都市文化新地标,面向世界展现千年巴蜀风韵.某数学兴趣小组在
探测东安阁高度的实践活动中,选取与阁底A在同一水平面的B,C两处作为观测点,测得 ,
, ,在C处测得阁顶 的仰角为45°,则他们测得东安阁的高度 为(精确
到 ,参考数据: , )( )A. B. C. D.
【答案】C
【解析】
【分析】在 中,由正弦定理可求 ,进而可得结果.
【详解】在 中,则 ,
因为 ,可得 (m),
在 中,则 ,
即 为等腰直角三角形,可得 (m).
故选:C.
5. 已知等差数列 的前 项和为 .若 , ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】设等差数列 的公差为 ,利用等差数列的求和公式求出 的值,再利用等差数列的求和公式
可求得 的值.【详解】设等差数列 的公差为 ,则 ,
又因为 ,则 ,解得 ,
因此, .
故选:C.
6. 已知点 是抛物线 的焦点,点 ,且点 为抛物线 上任意一点,则
的最小值为( )
A. 5 B. 6 C. 7 D. 8
【答案】C
【解析】
【分析】利用抛物线的定义求解即可.
【详解】因为点 是抛物线 的焦点,所以 ,解得 ,所以抛物线 的
方程为: .
由抛物线的定义知:点 到点 的距离等于点 到准线 的距离,
结合点 与抛物线 的位置关系可知, 的最小值是点 到准线 的距离,故
的最小值为7.
故选:C.7. 已知定义在 上的函数 , , , ,则a,b,
c的大小关系为( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据函数的奇偶性、单调性以及导数等知识确定正确答案.
【详解】 的定义域是 ,所以 是奇函数.
当 时, ,
所以 在 上单调递增. ,
由于 ,
所以 ,即 .
故选:B
8. 已知三棱锥 的顶点都在球 的球面上, 平面 ,若球 的体
积为 ,则该三棱锥的体积的最大值是( )
A. B. 5 C. D.
【答案】A
【解析】
【分析】将三棱锥 放入长方体内,得到 为球直径,由基本不等式求出 ,从而
求出三棱锥的体积的最大值.
【详解】因为 ,易知三角形 为等腰直角三角形,
又 平面 ,所以 为三棱锥 的高,则可将三棱锥 放入长方体内,如图,
长方体的体对角线即为外接球直径,即 为球直径,
,
解得 ,
又 ,
解得 ,
,所以
所以三棱锥的体积 ,
故选:A
【点睛】解决与球有关的内切或外接的问题时,解题的关键是确定球心的位置.对于外切的问题要注意球
心到各个面的距离相等且都为球半径;对于球的内接几何体的问题,注意球心到各个顶点的距离相等,解
题时要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形,利用勾股定理求得球的
半径
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项
符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列命题中是真命题的是( )
A. “ ”是“ ”的充分不必要条件
B. 命题“ , ”的否定是“ : , ”C. 把 的图像向左平移 个单位长度,得到的图像的解析式为
D.
【答案】ABD
【解析】
【分析】根据充分条件、必要条件的定义判断A,根据全称量词命题的否定为特称量词命题判断B,根据
三角函数的变换规则及诱导公式判断C,根据余弦函数的性质判断D;
【详解】解:对于A:由 ,即 ,解得 或 ,所以由 推得出 ,
由 推不出 ,所以 是 的充分不必要条件,故A正确;
对于B:命题“ , ”的否定是“ : , ”,故B正确;
对于C:把 的图像向左平移 个单位长度,得到 ,故C错误;
对于D:因为 在 上单调递减,又 ,所以 ,所以 ,故D正
确;
故选:ABD
10. 如图是函数 的导函数的图象,对于下列四个判断,其中正确的是( )
A. 在 上 是增函数
B. 在 上是减函数
C. 当 时, 取得极小值D. 当 时, 取得极大值
【答案】BC
【解析】
【分析】根据导数与原函数关系解决.
【详解】从导函数图像可以看出函数 在 上为单调减函数;
在 上为增函数,故A错B对,C对D错.
故选:BC
11. 已知双曲线 的左、右焦点分别为 ,抛物线 的焦点与双曲线C的
一个焦点重合,点P是这两条曲线的一个公共点,则下列说法正确的是( )
A. B. 的周长为16
C. 的面积为 D.
【答案】AB
【解析】
【分析】根据双曲线的焦点即可求解抛物线的定义,即可判断A,联立双曲线方程与抛物线方程,即可求
解交点坐标,利用点点距离即可求解长度,即可判断BC,由余弦定理即可判断D.
【详解】由已知,双曲线右焦点 ,即 ,故A项正确.且抛物线方程为 .
对于B项,联立双曲线与抛物线的方程 ,
整理可得. ,解得 或 (舍去负值),
所以 ,代入 可得, .
设 ,又 ,所以 , , ,则 的周长为16,故B项正确;
对于C项,易知 ,故C项错误;
对于D项,由余弦定理可得, ,故D项错
误.
故选:AB
12. 如图,正方体 的棱长为 ,E是棱 上的动点(不包含端点),则下列说法正确
的是( )
A. 若E为 的中点,则直线 面
B. 三棱锥 的体积为定值
C. 直线AC与直线 所成角为定值
D. 直线 与平面 所成角正切值的范围为
【答案】BCD
【解析】【分析】若 为 中点,连接 ,判断 为平行四边形,结合 面 判断A;由
,数形结合及棱锥体积公式判断B;根据正方体性质及线面垂直的判定、性质判断C;
根据线面角定义求其正切值的范围判断D.
【详解】A:若 为 中点,连接 ,又E为 的中点,正方体中易知 ,
所以 为平行四边形,则 ,而 面 ,显然 面 不成立,错;
B: ,显然 的面积为定值,且 到面 的距离为定值,
所以三棱锥 的体积为定值,对;
C:由题意 且 面 , 面 ,则 ,
, 面 ,则 面 ,而 面 ,
所以 ,直线AC与直线 所成角为定值,对;D:由上 到面 的距离为a,而E是棱 上的动点(不包含端点),
所以 ,则直线 与面 所成角正切值 范围为 ,对.
故选:BCD
三、填空题:本题共4小题,每小题5分,共20分.
13. 若向量 、 为单位向量,且 则向量 与 的夹角为________.
【答案】 ##
【解析】
【分析】根据模长公式即可代入求解.
【详解】由 可得 ,
可得 ,
由于 ,所以 ,
故答案为: .
14. 已知正项等比数列 的前 项和为 ,若 ,且 ,则 __________.
【答案】
【解析】
【分析】根据条件求等比数列的基本量及等比数列求和公式计算即可.【详解】设公比为 ,则 ,
由 , ,
解之得 或 (舍去),
故 .
故答案为:
15. 已知函数 为奇函数, ,若当 时, ,则
______.
【答案】
【解析】
【分析】根据函数的周期性、奇偶性以及对数运算求得正确答案.
【详解】所以 ,
所以 是周期为 的周期函数,
又函数 为奇函数,当 时, ,
所以 ,即 ,可得 ,
则 .
故答案为:
16. 已知⊙M: ,直线l: ,点P为直线l上的动点,过点P作⊙M的
切线 ,切点为A,则切线段 长的最小值为________.
【答案】1【解析】
【分析】由已知求得圆心坐标与半径,再求出圆心到直线l的距离,利用勾股定理得答案.
【详解】⊙M: 的圆心坐标为 ,半径为2,如图,
,且 ,
故要使 最小,则 最小,此时PM⊥l,
因为圆心M到直线l: 的距离为 ,
∴ 的最小值为
故答案为:1.
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17. 已知向量 , ,设函数 .
(1)求 的最小正周期;
(2)求 在 上的最大值和最小值.
【答案】(1)
(2)最大值1,最小值 .
【解析】
【分析】(1)利用三角恒等变换公式和辅助角公式化简表达式即可求解;
(2)求函数在给定区间内的最大值和最小值即可求解.
【小问1详解】由题意得 ,
所以函数的最小正周期为 .
【小问2详解】
因为 ,所以 ,所以 ,
所以当 即 时函数有最大值为1,
当 即 时函数有最小值为 .
18. 在三棱锥 中, ABC是边长为4的正三角形,平面 平面 , ,
△
、 分别为 的中点.
(1)证明: ;
(2)求二面角 正弦值的大小.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)取AC得中点O,得 , ,可知 平面 ,进而得结论;
(2)建立空间直角坐标系,求出平面CMN与平面 的法向量,根据向量的夹角公式求解.
【小问1详解】
取AC得中点O,连接SO,OB,, , , ,
又SO,BO交于点O, 平面 , 平面 ,
于是可知 平面 ,
又 平面 , ;
【小问2详解】
∵平面 平面 ,平面 平面 , 平面 , ,
∴ 平面 ,
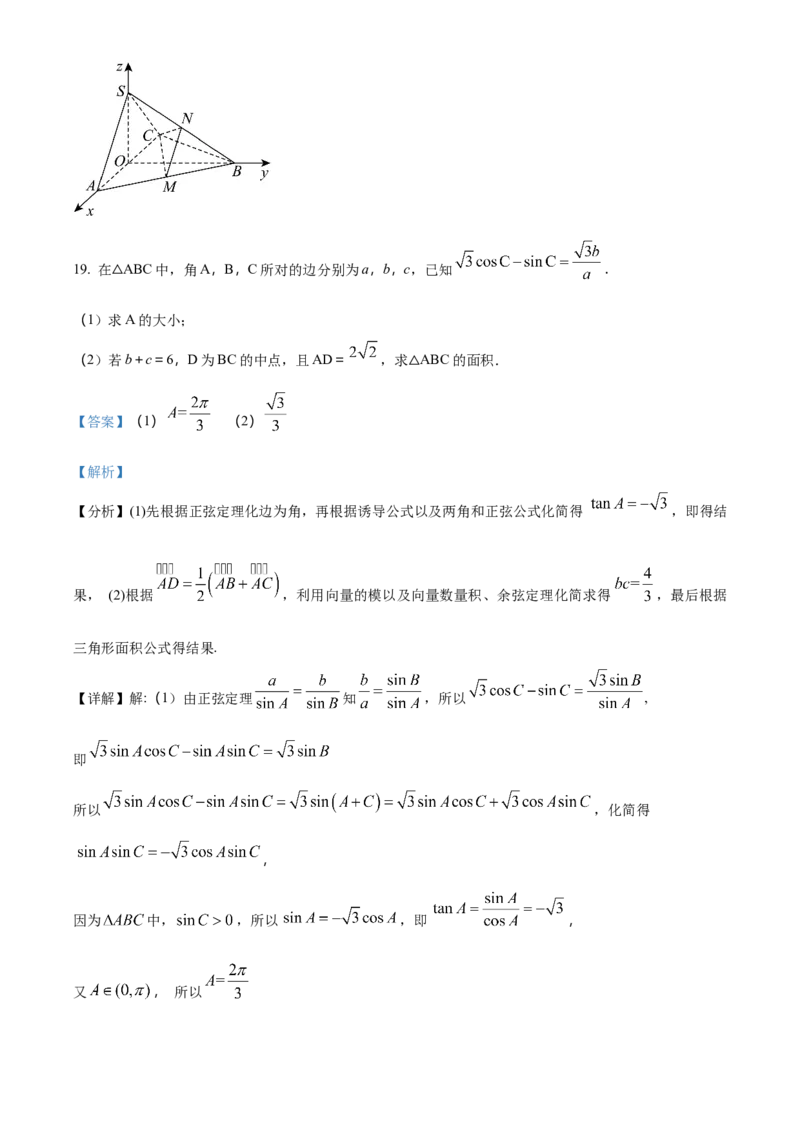
以OA为x轴,OB为y轴,OS为z轴建立空间直角坐标系 ,
那么 ,
∴ ,
设 为平面CMN的一个法向量,
那么 ,取 ,那么 ,
∴ ,
的
又 为平面 一个法向量,
, ,
即二面角 的正弦值为 .19. 在 ABC中,角A,B,C所对的边分别为a,b,c,已知 .
△
(1)求A的大小;
(2)若b+c=6,D为BC的中点,且AD= ,求 ABC的面积.
△
【答案】(1) (2)
【解析】
【分析】(1)先根据正弦定理化边为角,再根据诱导公式以及两角和正弦公式化简得 ,即得结
果, (2)根据 ,利用向量的模以及向量数量积、余弦定理化简求得 ,最后根据
三角形面积公式得结果.
【详解】解:(1)由正弦定理 知 ,所以 ,
即
所以 ,化简得
,
因为 中, ,所以 ,即 ,
又 , 所以(2)因为 ,
所以
,
由 ,解得
所以 的面积
【点睛】解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理以及三角形面积公式结合已
知条件灵活转化边和角之间的关系,从而达到解决问题的目的.
20. 设数列 的前 项和为 ,已知 .
(1)求 的通项公式;
(2)设 ,求数列 的前 的项和 .
【答案】(1)
(2)
【解析】
【分析】(1)由 ,得 ,两式相减化简可得数列 是以1为首项,
3为公比的等比数列,从而可求出其通项公式,
(2)由(1)得 ,然后分别利用分组求和,错位相减法求出奇数项的和与偶数项的
和,相加即可.
【小问1详解】由 ,得 ,两式相减得 .
令 数列 是以1为首项,3为公比的等比数列,
【小问2详解】
由题意可得 ,
,
①,
则 ②,
① ②得: ,
∴ ,
21. 已知椭圆 的两个焦点分别为 、 ,离心率为 ,过 的直线 与椭圆
交于 、 两点,且 的周长为 .
(1)求椭圆 的方程;
(2)求 面积的最大值.
【答案】(1)(2)
【解析】
【分析】(1)依题意可得 ,解得 、 ,即可求出椭圆方程;
(2)设直线 的方程为 , , ,联立直线与椭圆方程,消元、列出韦达
定理,则 ,代入可得 ,再令 ,根据对勾函数的性
质计算可得.
【小问1详解】
解:依题意可得 ,解得 ,
所以椭圆方程为 .
【小问2详解】
解:由(1)可得 ,
设直线 的方程为 , , ,
由 ,消去 整理得 ,
所以 , ,所以
,
令 ,则 ,
所以 ,又 在 上单调递增,
所以 ,当且仅当 时取等号,即当 时 面积的最大值为 .
22. 已知函数 ,其中 .
(1)讨论 的单调性;
(2)设 ,若不等式 对 恒成立,求 的取值范围.
【答案】(1)答案见解析
(2)
【解析】
【分析】(1)求导,分 和 两种情况,利用导数判断原函数单调性;
(2)结合(1)可得 ,令 ,利用导数解不等式即可.
【小问1详解】
由题意可知: 的定义域为 ,且 ,
当 时, 恒成立,则 在 上单调递减;当 时,令 ,解得 ;令 ,解得 ;
则 在 上单调递减,在 上单调递增;
综上所述:当 时, 的单调减区间为 ,无单调增区间;
当 时, 的单调减区间为 ,单调增区间为 .
【小问2详解】
当 时,由(1)可知 在 上单调递减,在 上单调递增,
故 的最小值为 .
因为不等式 对 恒成立,所以 .
设 ,
则 的定义域为 ,且 恒成立,
可知: 在 上单调递增.
因为 ,所以 ,
即 ,可得 ,即 .
综上所述: 的取值范围是 .