品优教学高中数学总复习知识点分类网络结构图(大全·精华)_赠送小初高学霸笔记等_小初高知识点_小初高知识点_高考数学知识点

集合 集合与简易逻辑 集合间的关系与运算 简易逻辑 映射与函数 函 映射与函数 函数的三要素 数 函数的图象 单调函数与函数的单调性 函数的性质与反函数 函数的奇偶性 反函数及其图象 正比例函数、反比例函数、一次函数、二次函数 幂函数 初等函数 指数与指数函数 对数与对数函数 函数的应用 函数的应用集合的基本概念 元素与集合的关系 特定集合的记法 N（自然数集）、Z（整数集）、Q（有理数集）、R（实数集）、C（复数集） 集合 对集合概念的理解 集 空集的特殊性 合 集合语言与数学语言的互译 与 简 集合与集合的关系 易 ①，（A、B代表任意集合） 逻 ②，则 辑 ③ ④若A中元素有n个，则A的子集共有个，真子集有个 集 合 与 集 合 间 的关系 集合间的运算 数形结合解集合问题 注意交集思想、并集思想、补集思想的运用 命题 简 易 逻 反证法 辑 充分条件与必要条件 逻辑与集合思想映射的概念 函数的概念 映射与函数的关系 表示函数的符号 映射与函数 函数的表示法 映 复合函数的定义 射 与 区间的概念 函 数 函数方程 函数三要素 定义域、值域、对应法则，三者缺一不可。 函数的定义域 函数的值域 函数三要素 函数的解析式 函数定义域的求法 函数值域的求法 用值域求最值 求解函数解析式 描点法作图 函数的图象 函数图象的变换 坐标变换单调函数的定义 单调函数的特点 单调函数与函数的单 利用单调性求极值 调性 函 利用单调性解方程 数 的 单调函数与二次方程结合 性 质 奇偶函数的定义 与 反 函数的奇偶性 奇偶函数的性质 函 数 奇偶函数与周期函数的结合 反函数的定义 反函数的一些性质 反函数及其图象 反函数求值域或定义域 反函数解不等式 指数函数的定义 指数与 指数函数的图象 指数函 数 指数函数的性质 指数函数与方程 初 等 指数函数的单调性 函 数 对数的有关概念 对数函数的定义 对数函数的图象 对数与 对数函 对数函数的性质 数 求对数的极值 对数方程初等函数及其分类 初等函数是能用一个解析式表示的函数，它分为超越函数和代数函数两 种（超越函数包括指数是无理数的幂函数、指数函数、对数函数、三角和反 三角函数），一共有15个约定的模型函数，我们一般研究七个： ①若（k ），那么，y叫做x的正比例函数 ②若（k是常数，），那么，y叫做x的反比例函数 ③若（k，b是常数，），那么，y叫做x的一次函数 ④若（a，b，c为常数，），则y叫x的二次函数 ⑤函数叫做幂函数，其中x是自变量，a是常数 ⑥函数叫做指数函数，其中a为常量且a＞0且a≠1 ⑦若（a＞0且a≠1），则b叫做以a为底N的对数，记做，其中a叫底 数，N叫真数 正比例 函数、 反比例 函数、 一次函 数、二 次函数 初 等 初等函数的定义、图象、性质 函 数 二次函数、二次方程、二次不等式 二次函数图象交点问题 函数极值的求法 函数解析式的求法 幂函数的定义 幂函数的图象 幂函数 幂函数的性质 幂函数的奇偶性和单调性不等式的性质 不等式 算术平均数与几何平均数 不等式的证明 不 不等式的证明 等 解不等式 式 不等式的拓展 含有绝对值的不等式 不等式的应用 不等式的概念 不等式的基本性质 ①（对称性）②（传递性） ③④ ⑤ ⑥ 不等 ⑦ 式的 性质 比较法解不等式 等号成立条件 不 等 分类思想的应用 式 重要结论的充分应用 基本不等式 ①②若则③ 算 数 ④若则 平 均 数 与 几 何 平 均 数 不等式的最值问题 不等式、三角函数和三角形的结合比较法 综合法 分析法 反证法 不 换元法 等 放缩法 式 的 判别式法 证 明 数学归纳法 解不等式的概念 不等式的同解变形原理：①对任何一个不等式，为任一关于的代数式，与同解； ②若，则不等式与不等式同解。 不 整式不等式的解法 等 (1) 的解 式 ①，不等式的解为； 的 ②，不等式的解为； 证 ③，不等式的解为R． 明 (2)的解 ①，不等式的解为； ②，不等式的解为． 解 不 等 式 分式不等式的解法 与同解 与同解无理不等式的解法 ①与不等式组或同解 ②与不等式组同解 ③与不等式组 同解 解 指数不等式的解法 不 ① 等 ② 式 对数不等式的解法 ①时与同解 ②时与同解 不 等 式 的 分类讨论思想的应用 证 明 绝对值的定义和性质 绝对值不等式的同解变形 含 ① 有 ② 绝 ③ 对 值 的 不 等 式 证 明 绝对值不等式的证明 一般要利用的性质来证明平均值不等式 当且仅当时取等号 柯西不等式 当且仅当时取等号 排序不等式 著 名 不 复数模不等式 等 是复数，则①当时，当且仅当时右等号成立； 式 时左等号成立②当且仅当辅角相等时等号成立 琴生不等式 设在区间内下凸，是区间内的任意数，有 （其中）。上凸函数不等号转向. 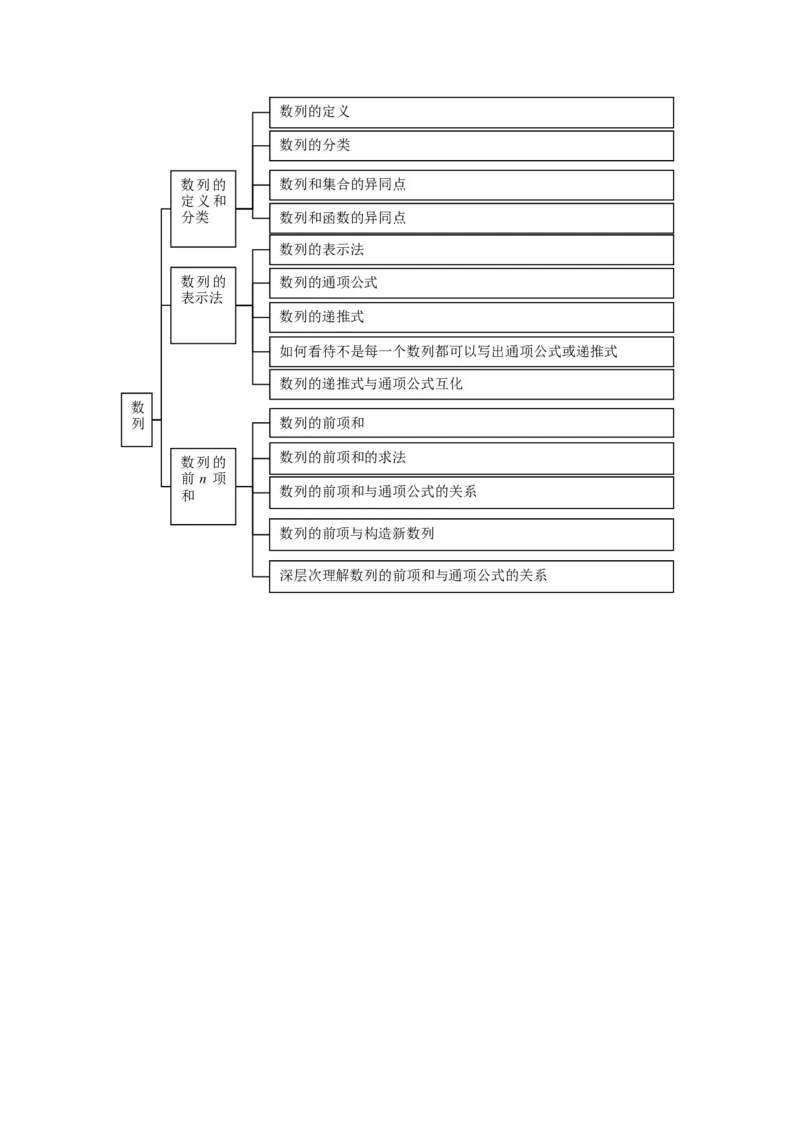不 等 式 拓 展 比较法 要证明，通常作差比较,或作商比较 证 明 不 分析综合法 等 式 数学归纳法 的 常 放缩法 用 方 变量代换法 法 构造法 局部调整法一元二次方程的实根分布问题 不等式求函数的极值 不 等 式 的 应用 不等式在实际生产生活中的应用题 椭圆不等式的应用和推广 数列的定义和分类 数列 数列的表示法 数列的前n项和 等差数列 数列、 极限、 数 学 等差数列的前n项和 归 纳 等差数列 法 等差数列的性质 等比数列 等比数列 等比数列的前项和 等比数列的性质 数列的极限 数列的极限 和数学归纳 法 数学归纳法 数列的应用 数列的应用 限和数学归 纳法数列的定义 数列的分类 数列的 数列和集合的异同点 定义和 分类 数列和函数的异同点 数列的表示法 数列的 数列的通项公式 表示法 数列的递推式 如何看待不是每一个数列都可以写出通项公式或递推式 数列的递推式与通项公式互化 数 列 数列的前项和 数列的前项和的求法 数列的 前 n 项 数列的前项和与通项公式的关系 和 数列的前项与构造新数列 深层次理解数列的前项和与通项公式的关系等差数列的定义 等差数列的通项公式 等差中项 等 等 差 如果三个数成等差数列，那么叫做的等差中项，且.和的等差中项也称为和的 差 数列 算术平均数 数 列 等差数列的通项公式是如何得到的 等差数列递推式的变形及应用 等差数列和一次函数的异同点 等差数列的前项和 等 差 数 列 的前 项和 等差数列的判定 等差数列的前项和公式和二次函数的关系 等差数列的基本性质 ①②③若m+n=k+l，其中m，n，k，l均为自然数，则必有④等差数列中，其项 数成等差的项构成的一个子数列仍是等差数列⑤等差数列的每一项都加上一 个常数（或乘以一个非零实数k）仍然构成一个与原等差数列，公差不变（或 变为原来的k倍） 等 差 数 列 的 性 质 等差数列若干项和的性质 将公差为d的等差数列截为k段，每段具有m项，则每段各项之和组成的新数 列为等差数列，其公差为等比数列的定义 等比数列的通项公式 其中，q分别是首项和公比，n为项数，n∈N 等比中项 等 等 比 如果三个数成等比数列，那么叫做和的等比中项，且，。x和y的等比中项也称 比 数列 为x和y的几何平均数。 数 列 等比数列的通项公式是如何得到的 等比数列递推式的变形及应用 等比数列和指数函数的异同点 等比数列的前项和 等 比 数 列 的前 项和 等比数列的判定 等比数列的概念扩展 等比数列的基本性质 ①②③若m，n，k，l均为自然数，且，则必有④其项数成等差的项构成的一 个子数列仍是等比数列⑤若数列为无穷等比数列，其公比为q，则对任意正整 数m，数列仍是等比数列，其公比为 等 比 数 列 的 性 质 等比数列若干项积的性质 等比数列若干项和的性质 递推数列的一阶特征方程数列的极限 数列极限的运算法则 若=A，=B，①则=A±B； ②当C为常数时，（C）=CA；（B≠0） 数 列 的 极 限 无穷数列的所有项的和 无穷递缩等比数列的各项和记作S， 则 数 列 的 极 怎样理解数列的极限 限 和 数 如何求简单数列的极限 学 归 演绎法和归纳法 纳 数 法 完全归纳法和不完全归纳法 学 归 数学归纳法 纳 法 如何理解数学归纳法 如何运用数学归纳法 角的概念的推广、弧度制 三角函数 任意角的三角函数 同角三角函数关系式和诱导公式 三角变换 两角和与差的三角函数公式 三 倍角与半角的三角函数公式 角 函 三角函数的 三角函数的图像与性质 数 图像和性质 等比数列的性质 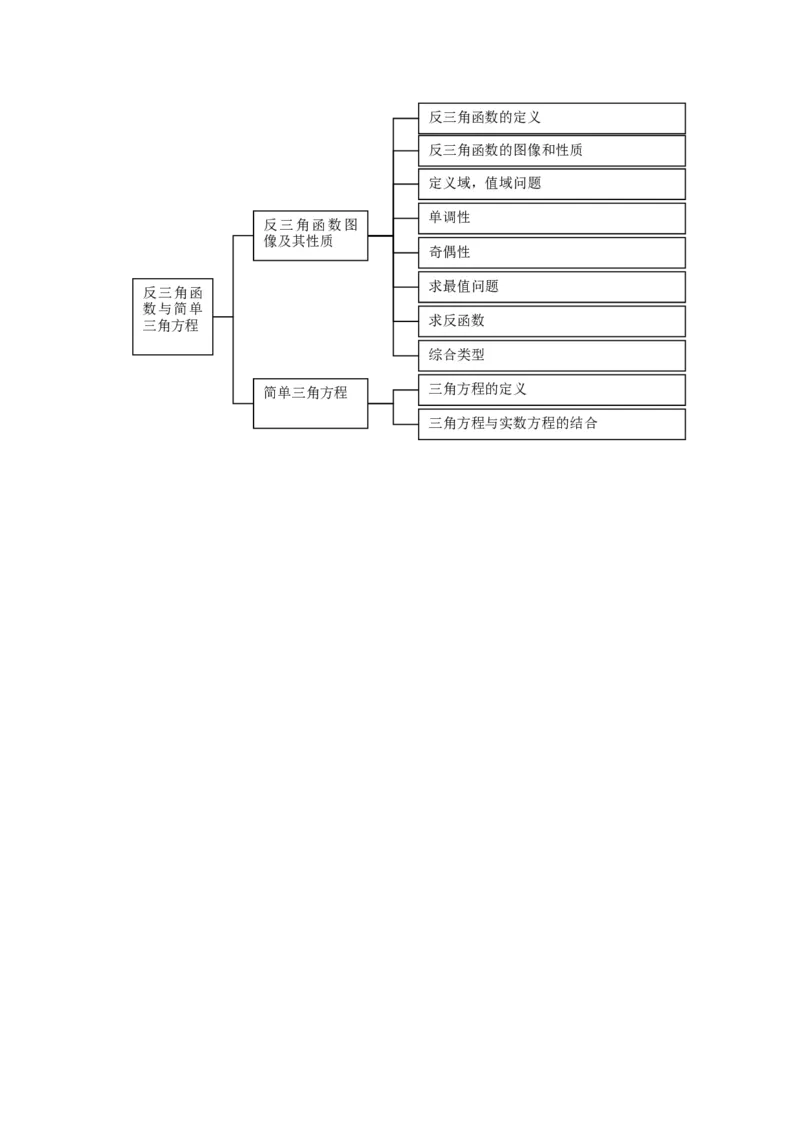反三角函数 反三角函数的图像和性质 与简单的三 角方程 简单三角方程 三角函数的 数列的应用 应用限和数 学归纳法角的概念 角的概念的推广 角 角的度量 的 概 念 弧度与实数的一一对应 的 推 广 任意角的三角函数 需要牢记的三角函数值 角 函 数 0°30°45°60°90°180°270°360°0 sin010-10cos10-101t an01不存在0不存在0cot不存在10不存在0不存在 三 角 函 数 任 意 角 的 三 角 函 数 三角函数线 弧长公式 任意角三角函数和与其对应的锐角三角函数的关系同 同角三角函数的基本关系 角 三 三角函数的诱导公式 角 “奇变偶不变，符号看象限” 函 数 如何记忆同角三角函数的基本关系 关 系 求任意角三角函数的步骤 式 和 三角函数的基本题型 诱 导 化归思想 公 式 整体代换法 三 两角和与差的三角函数公式 角 两 变 角 换 和 与 差 的 三 公式的推导 角 函 公式的运用 数 公 式 三角形中的三角函数关系式,判断三角形的形状 注意角度的各种存在形式 利用三角函数求最值问题倍角、半角公式 ①二倍角公式： ,②三倍角公式： ③半角公式： 倍 角 与 半 三 角 的 角 部分倍角、半角公式、和差化积、积化和差的推导 三 变 角 倍角、半角、和差化积、积化和差等公式的运用 换 函 数 万能公式的应用 公 式 三角函数在三角形中的应用反三角函数的定义 反三角函数的图像和性质 定义域，值域问题 单调性 反三角函数图 像及其性质 奇偶性 求最值问题 反三角函 数与简单 求反函数 三角方程 综合类型 简单三角方程 三角方程的定义 三角方程与实数方程的结合三角函数的图像 三 五点作图法 角 函 数 的 函数图像的坐标变换 图 象 求定义域和值域型 与 性 求最值型 质 三 求三角函数的周期与单调性 角 函 余弦定理 数 的 图 正 象 弦 和 定 性 理 质 、 正弦定理 余 弦 定 理 、 解 斜 斜三角形的解法 三 角 形 一些有用的结论 三角函数在三角形中的应用向量 向量的加减法 平面向量及 向量和实数的积 其运算 平面向量的数量积及运算率 平面向量的坐标表示及运算 平面向量的 坐标表示 向量的定比分点 向量 平移 空间向量及 空间向量 运算 空间向量的运算 向量的应用 向量的应用 限和数学归 纳法向量的定义 向量的模 零向量和单位向量 向量 平行向量、共线向量和相等向量 向量和有向线段 平 向量与标量 面 向 向量的相等与平行 量 及 向量的加法 其 运 算 向量的平行四边形法则 向 量 的 加 向量加法满足交换率和结合率 减法 向量的减法 向量减法的几何作法 对于向量三角形法则的补充 实数和向量积的定义 向 量 和 实 实数和向量积的运算率 数 的 积 两个向量公线定理 平面向量的基本定理 如何利用和证明向量的平行关系 向量方程的求解 平 面 向 量 平面向量数量积的定义和几何意义 的 数 量 积 向量数量积的性质 及 运 算 律 向量数量积的运算率 学 归 纳法 向量数量积运算与普通乘法运算的比较 用i、j坐标表示下向量的数量积平面向量的坐标表示 向量的模 若=(x,y),则 |a|2= · =x2+y2,∴| |= 平 面 两点间的距离公式 向 量 设A(x,y),B(x,y)，则| | 1 1 2 2 的 坐 标 表 示 及 两个非零向量垂直的充要条件的坐标表示 平 运算 若=(x,y), =(x,y)，则⊥xx+yy=0 面 1 1 2 2 1 2 1 2 向 量 两向量的夹角公式的坐标表示 的 =(x,y), =(x,y)的夹角的余弦 坐 1 1 2 2 标 表 示 平面向量的坐标运算 向量的坐标与表示该向量的有向线段的起始点位置无关 仿射坐标系的思想 向量的平行和垂直的判定 点P分有向线段所成的比的定义 定比分点公式，中点公式及其推导 线 段 ,设P(x,y)，P(x,y)，P(x,y)分所成比为，则 (λ≠-1) 的 定 1 1 1 2 2 2 比 分 点 定比分点的几个重要公式 平移 图形的平移 平移公式 利用平移公式化简函数解析式 平移图像是平移图像的每一点空间向量的概念 空间向量的表示方法 i=（1，0，0），j=（0，1，0），k=（0，0，1）.若a=（x，y，z），则a=xi+yj+zk 相等向量的内涵 空间直角坐标系中的坐标 向量的坐标 空间向量的直角坐标运算律 若，， 则①， ， ②， ③若，则． 空 间 向 量 模长公式 若，则． 夹角公式 两点间的距离 空间的向量 平面向量与空间向量空间向量的运算 运算律：⑴加法交换律：⑵加法结合律： ⑶数乘分配律： 平行六面体 空间向量的加减与数乘 =a+b， ， 空间向量的加减与数乘运算律 ⑴加法交换律：a + b = b + a⑵加法结合律：(a + b) + c =a + (b + c)； ⑶数乘分配律：λ(a + b) =λa +λb． 空 空间向量的夹角 间 向 向量的数乘积 量 的 运 算 空间向量数乘积的性质 ①．②．③． 空间向量数量积运算律 ①②（交换律） ③（分配律）④ea = ae =|a|cos ⑤ab  ab = 0⑥当a与b同向时，ab = |a||b|；当a与b反向时，ab = |a|| b|.特别的aa = |a|2或⑦⑧|ab| ≤ |a||b| 空间共面向量定理及推论 空间任意一向量可表示为，不共面， 空间向量的基本定理 利用空间两个向量平行的条件 数量积与互相垂直的等价关系 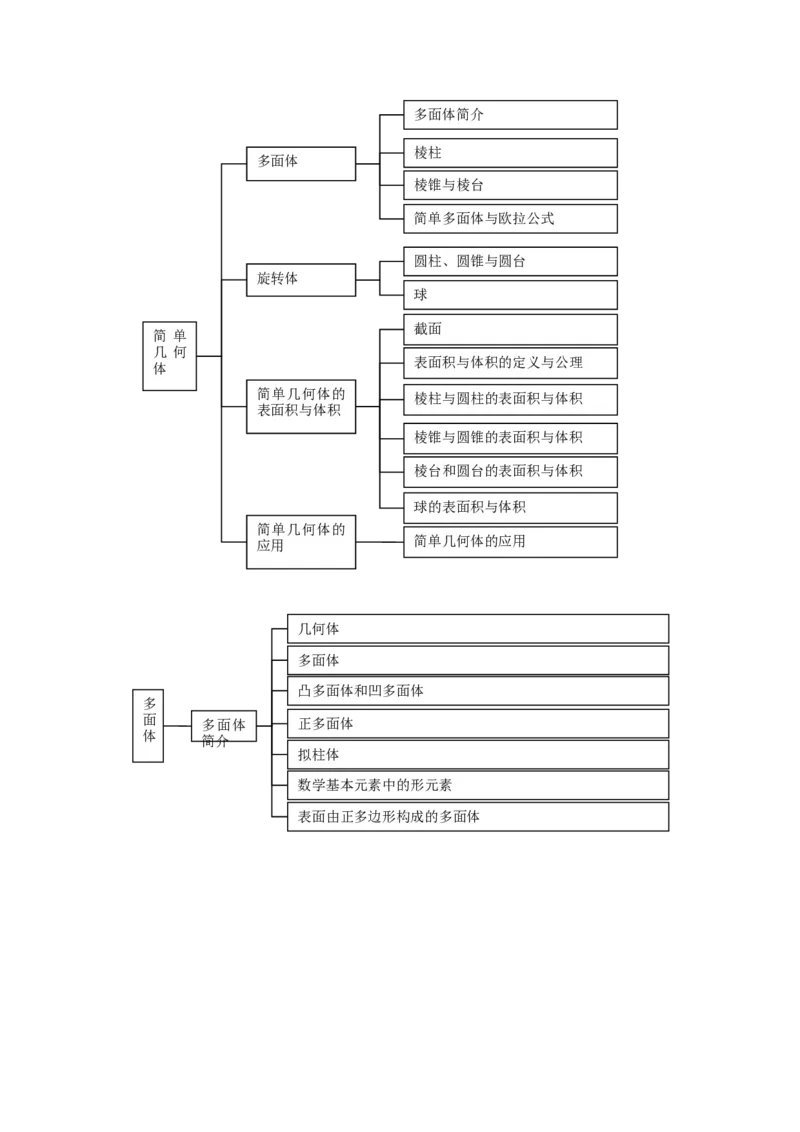数量积求角度，求点的坐标多面体简介 棱柱 多面体 棱锥与棱台 简单多面体与欧拉公式 圆柱、圆锥与圆台 旋转体 球 截面 简 单 几 何 表面积与体积的定义与公理 体 简单几何体的 棱柱与圆柱的表面积与体积 表面积与体积 棱锥与圆锥的表面积与体积 棱台和圆台的表面积与体积 球的表面积与体积 简单几何体的 简单几何体的应用 应用 几何体 多面体 凸多面体和凹多面体 多 面 多面体 正多面体 体 简介 拟柱体 数学基本元素中的形元素 表面由正多边形构成的多面体棱柱 斜棱柱与直棱柱 平行六面体 长方体三度定理及推论 长方体一条对角线长的平方等于一个顶点上三条棱的长的 棱柱 平方和；若长方体对角线和各棱所成的角分别为，和各面所 成角分别为，则; 特殊四棱柱之间的联系 多 简单几何体中的空间直线与平面 面 体 棱锥 正棱锥 棱锥与 棱锥的斜高 棱台 棱台 正棱台 棱台和棱锥相关问题的转化 简单多面体 如何证明欧拉公式 欧拉公式 简单多面体的顶点数V、棱数E、面数F，则有 简单多 面体与 欧拉定 理 欧拉示性数 欧拉公式中，令，那么叫做欧拉示性数 正多面体的种数 正多面体只有五种：正四面体、正八面体、正六面体、正十二面体和正 二十面体旋转面 圆柱面 圆 柱 圆锥面 圆 锥 与 圆 旋转体 台 圆柱 圆台 为什么说旋转体的轴截面是研究旋转体的主要工具 球面 球 球的大圆和小圆 旋 转 经线和纬线 体 两点的球面距离 球的切面和切线 球的内结圆台 球扇形 球冠和球冠面积公式 球面被平面所截得的一部分叫做球冠。截得的圆叫做球冠的底，垂 直于截面的直径被截得的一段叫做球冠的高。如果球冠所在球半径为R， 球冠高为h，球冠面积为S，则有 球 球带和球带面积公式 球面夹在两个平行截面之间的部分叫做球带，截得的两个圆叫做球带的 底，两个平行截面之间的距离叫做球带的高。如果球的半径是R，球带的 高是h，那么球带的面积 球缺和球台 环面和环体 简单多面体 怎么理解球类问题中的诸多概念截面 棱柱的截面 棱锥的截面 棱台的截面 圆柱的截面 截面 圆锥的截面 圆台的截面 球的截面 简 单 几 何 通过截面深层次体会降维思想 体 的 表 面 几何体的体积 积 与 体积 长方体体积公理及推论 设长方体的三棱长分别是a、b、c，则其体积 设长方体底面积为S，高为h，则其体积 设正方体棱长为a，则其体积为 表 面 积 祖暅原理 与 体 积 的 定 义 拟柱体的体积 和公理 如果拟柱体的上下底面的面积为和，中截面的面积为，高为，那 么它的体积 旋转体的体积 （1）柱体：； （2）锥体：； （3）台体；（4）球体：则。 几何体的表面积 拟柱体的侧面积和全面积 旋转体的侧面积和全面积 拟柱体的体积公式的证明思路棱柱的侧面积 设棱柱的底面周长为c，侧棱为l,则其侧面积 棱柱 与圆 圆柱的侧面积 柱的 设圆柱底面半径为r，侧棱为l，则其侧面积 表面 积与 体积 柱体的体积 若柱体的底面积为S，高为h，则其体积 推导体积公式的极限方法 棱锥的侧面积 ①正棱锥的侧面积等于底面周长与斜高的积的一半； ②若正棱锥的侧面与底面成角，则侧面积等于底面积乘以 棱锥 与圆 锥的 圆锥的侧面积 表面 ①圆锥的侧面积等于底面周长与母线的积的一半； 简单 积与 ②若圆锥母线与底面所成角为，则侧面积等于底面积乘以。 几何 体积 体的 表面 椎体的体积 积与 设锥体底面积为S，高为h，则有 体积 棱台的侧面积 棱台 ①正棱台的侧面积等于棱台的上下底面周长之和与斜高的积的一半； ②若正棱台的侧面与底面成角为，则等于上下底面积之差乘以 与圆 台的 表面 积与 圆台的侧面积 体积 台体的体积 台体的上、下底面的面积为，高为，则 球的表面积 设球的半径为R，则其表面积为 半球的侧面积 球的 设球的半径为R，则其表面积为 表面 积与 球的体积 体积 设球的半径为R，则其体积为 半球的体积 设球的半径为R，则其体积为平面的性质 平面 平面两直线的位置关系 空间两直线的位置关系 直线与直线的关系 两条异面直线所成角 直线与直线平行 直 线 直线和平面平行 与 直线与平面的关系 平 面 直线和平面所成角 平面和平面平行 二面角 几何中的平行关系和特 征角 异面直线上两点间距离 直线与平面的应用 直线与平面的应用面 面是没有厚度而只有位置和大小的几何图形 平面 可看成是由一条直线沿同一方向平行移动的轨迹 平面图形和空间图形 平面图形可看作是空间图形的一部分 平面的表示法 平面常用一个小写希腊字母表示，或用平面上的多边形的顶点字母表示 平 面 的 斜二测画法规则 定 义 从直线和平面的类比来理解平面 和 表 平面几何与立体几何的联系与区别 示 法 斜二测画法的本质与实际应用 平面的基本性质 平 平面的基本性质实际上就是关于平面的三个公理 面 公理1：若，则 公理2：若，则且 公理3：若，则A、B、C共面 平面基本性质的推论 这几个推论都是公理3的推论 。 平面的性质及推论的用途 平 性质1注药用语判定直线在平面内 面 性质2主要用来判断两面相交 的 性质3和推论都是确定一个平面的依据。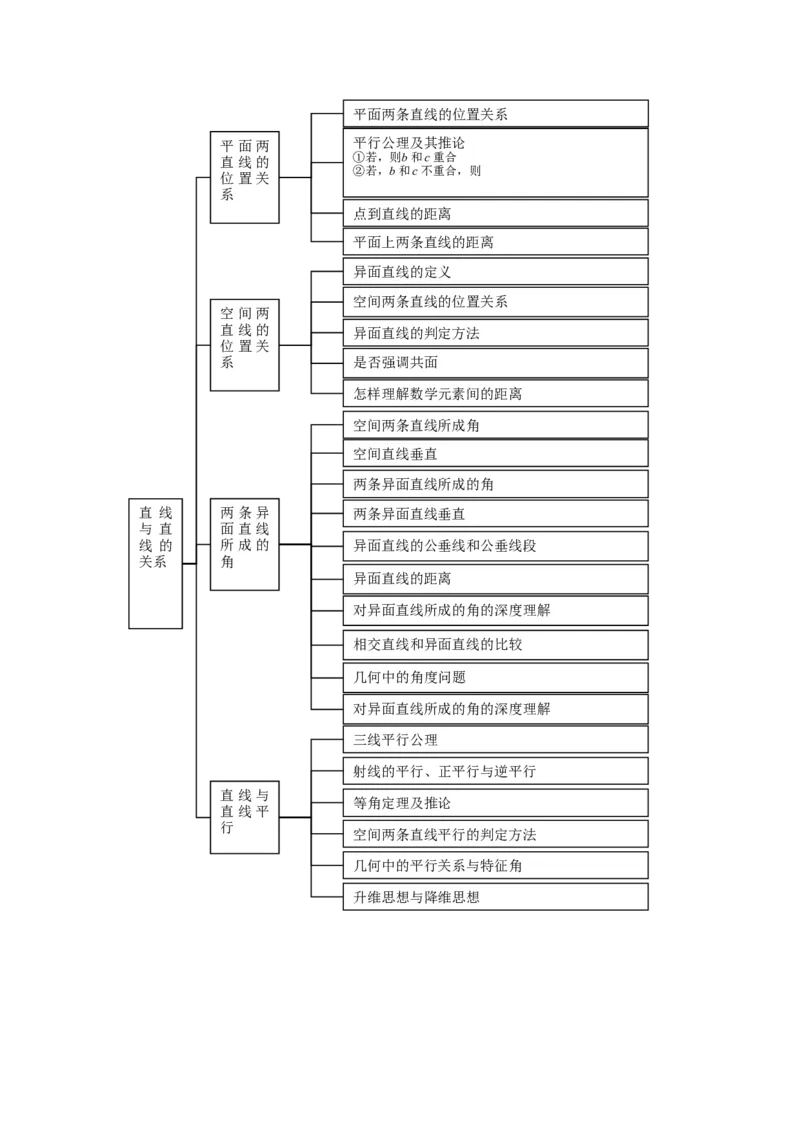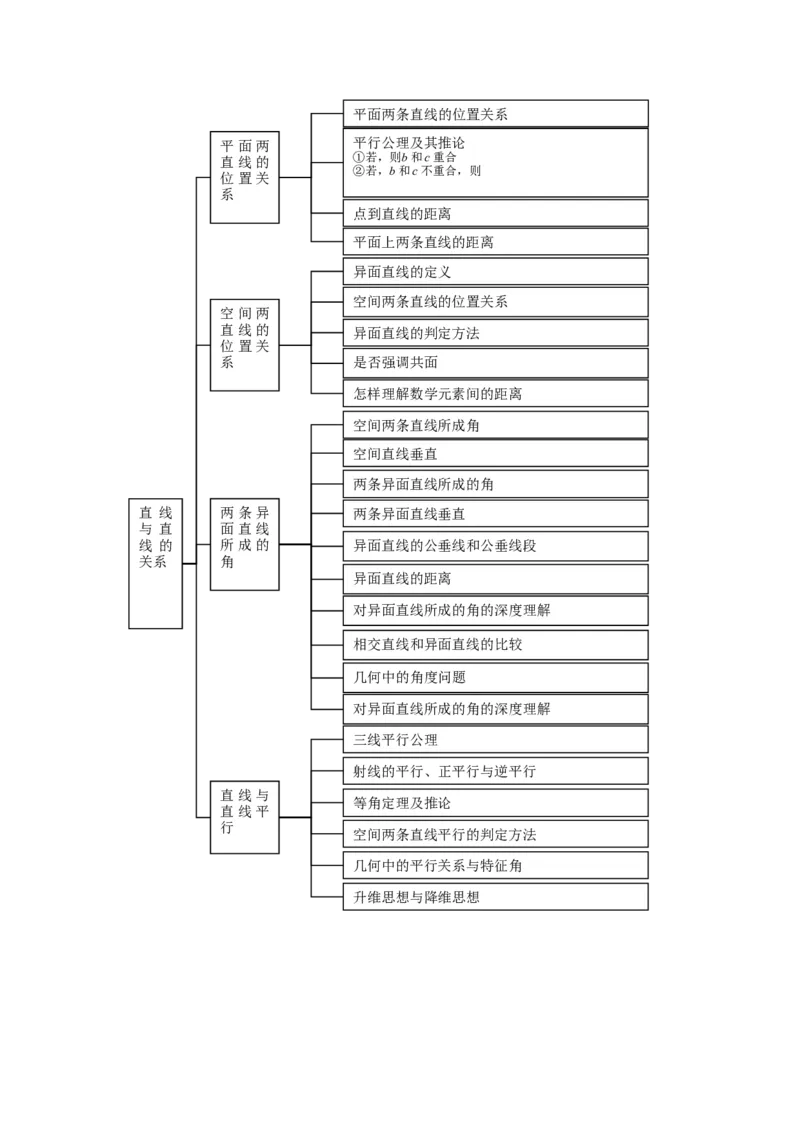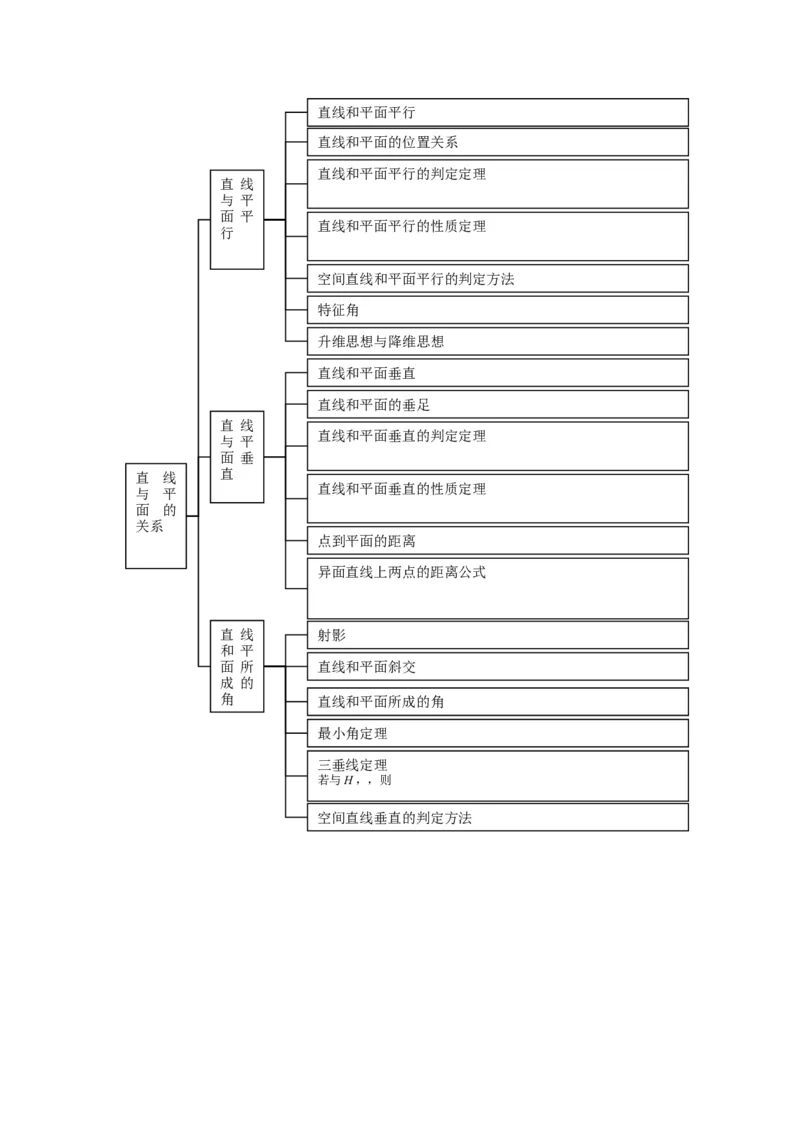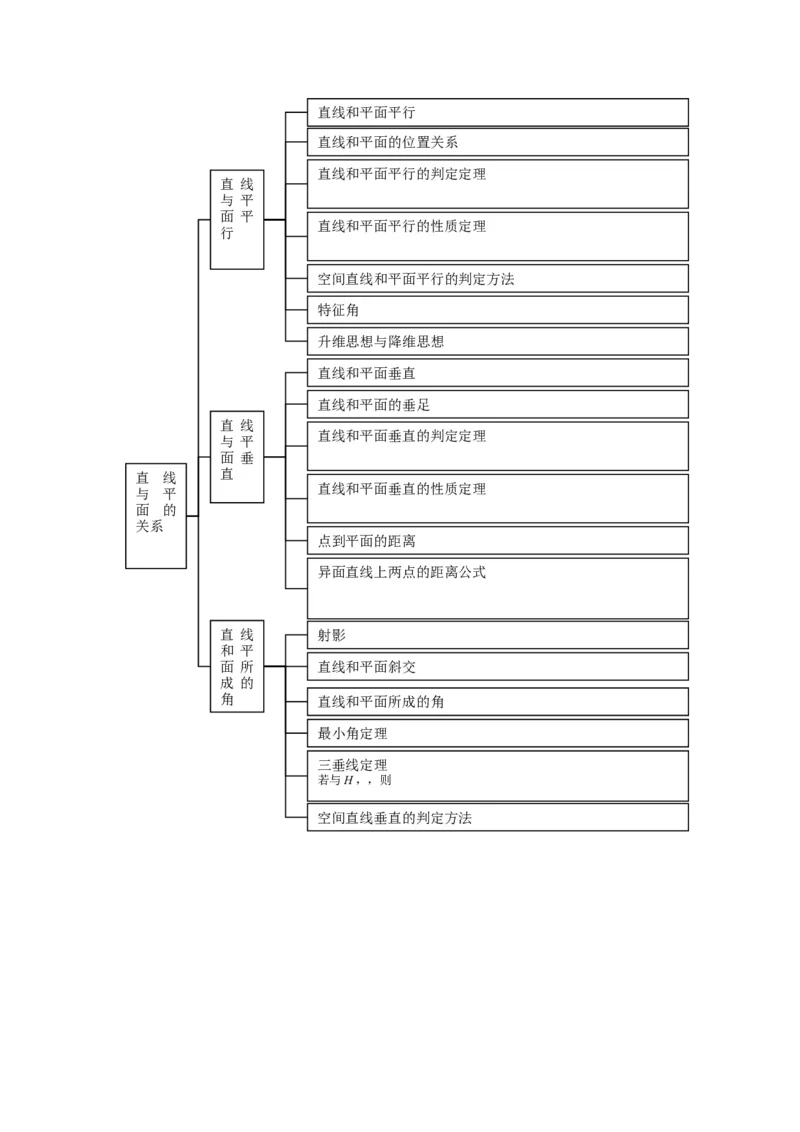 性 质 几何符号语言与常用语言的互化 平面的性质公理与推论的理解和运用平面两条直线的位置关系 平面两 平行公理及其推论 直线的 ①若，则b和c重合 ②若，b和c不重合，则 位置关 系 点到直线的距离 平面上两条直线的距离 异面直线的定义 空间两条直线的位置关系 空间两 直线的 异面直线的判定方法 位置关 系 是否强调共面 怎样理解数学元素间的距离 空间两条直线所成角 空间直线垂直 两条异面直线所成的角 直 线 两条异 两条异面直线垂直 与 直 面直线 线 的 所成的 异面直线的公垂线和公垂线段 关系 角 异面直线的距离 对异面直线所成的角的深度理解 相交直线和异面直线的比较 几何中的角度问题 对异面直线所成的角的深度理解 三线平行公理 射线的平行、正平行与逆平行 直线与 等角定理及推论 直线平 行 空间两条直线平行的判定方法 几何中的平行关系与特征角 升维思想与降维思想直线和平面平行 直线和平面的位置关系 直线和平面平行的判定定理 直 线 与 平 面 平 直线和平面平行的性质定理 行 空间直线和平面平行的判定方法 特征角 升维思想与降维思想 直线和平面垂直 直线和平面的垂足 直 线 直线和平面垂直的判定定理 与 平 面 垂 直 线 直 直线和平面垂直的性质定理 与 平 面 的 关系 点到平面的距离 异面直线上两点的距离公式 直 线 射影 和 平 面 所 直线和平面斜交 成 的 角 直线和平面所成的角 最小角定理 三垂线定理 若与H，，则 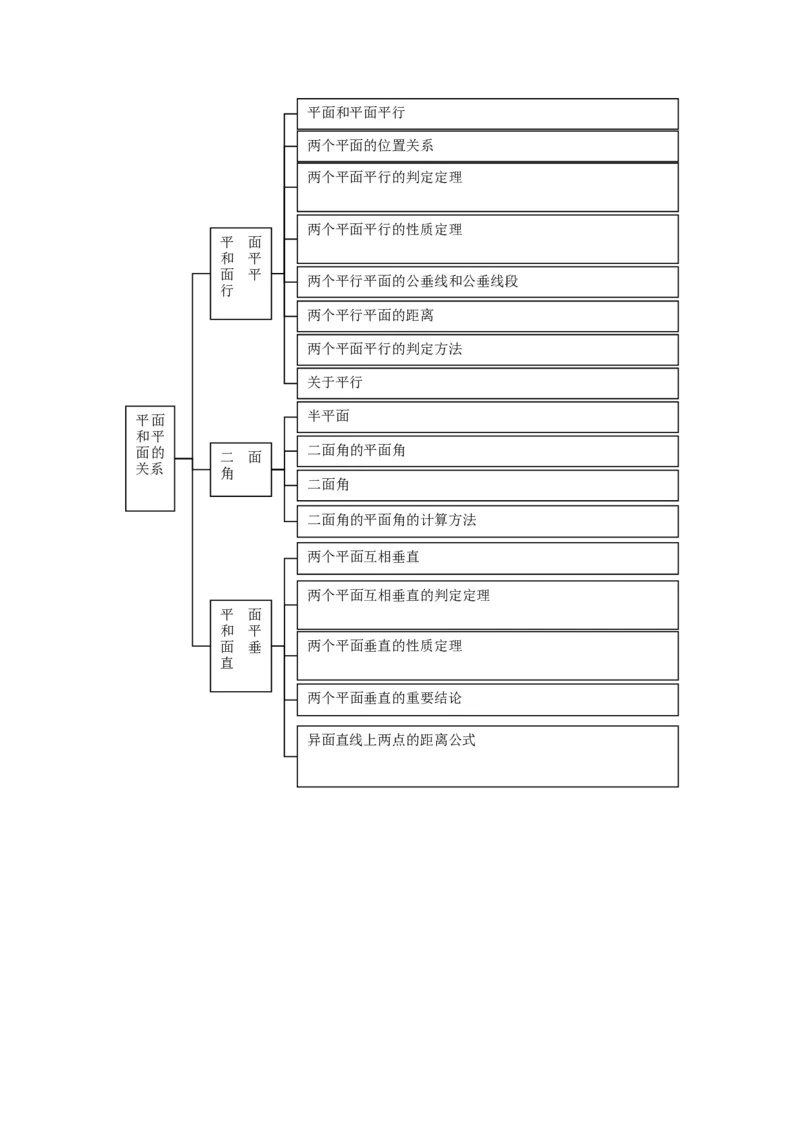空间直线垂直的判定方法平面和平面平行 两个平面的位置关系 两个平面平行的判定定理 两个平面平行的性质定理 平 面 和 平 面 平 两个平行平面的公垂线和公垂线段 行 两个平行平面的距离 两个平面平行的判定方法 关于平行 半平面 平面 和平 面的 二面角的平面角 二 面 关系 角 二面角 二面角的平面角的计算方法 两个平面互相垂直 两个平面互相垂直的判定定理 平 面 和 平 面 垂 两个平面垂直的性质定理 直 两个平面垂直的重要结论 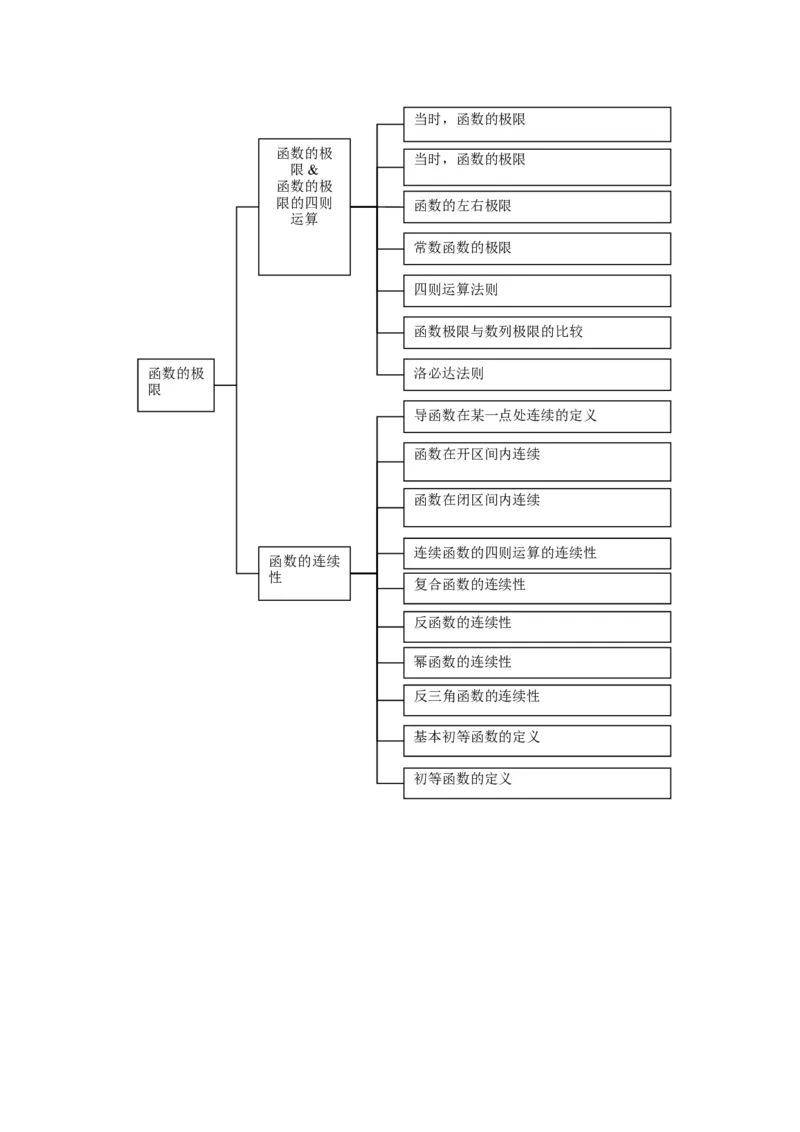异面直线上两点的距离公式函数的极限&函数的极限的四则运算 函数的极限 函数的连续性 导函数的概念和常见函数的导数 极限、导 导数 数和微积 函数求导法则及复合函数的导数 分 微分及四则运算 微积分 不定积分 定积分 导数与微分的应用 导数和微积分的 应用 积分的应用当时，函数的极限 函数的极 当时，函数的极限 限& 函数的极 限的四则 函数的左右极限 运算 常数函数的极限 四则运算法则 函数极限与数列极限的比较 函数的极 洛必达法则 限 导函数在某一点处连续的定义 函数在开区间内连续 函数在闭区间内连续 连续函数的四则运算的连续性 函数的连续 性 复合函数的连续性 反函数的连续性 幂函数的连续性 反三角函数的连续性 基本初等函数的定义 初等函数的定义处的导数 若极限存在，则称此极限值为函数在点处对的导数 导 函 导函数 数 的 概 念 导数的几何意义 和 常 见 导数公式 函 ①②③④⑤⑥⑦⑧⑨ 数 的 导 数 可导与连续的关系 二阶导数 n阶导数 求导法则 和（或差）的导数,积的导数,商的导数 导 数 函 复合函数的导数 数 求 导 法 对数函数求导 则 ①②③ 及 复 合 函 连续函数的四则运算的连续性 数 的 隐函数的求导 导 数 含参函数的求导 如果函数，由方程所确定，我们有微分的定义 微 分 四则运算 及 ，， 四 则 运 算 微分的本质： 原函数 若则称为在的一个原函数 微 不定积分 积 的全体原函数称为其不定积分，记作 分 初 步 基本积分公式 ①②③ 不 ④⑤⑥ 定 积 分 不定积分的运算法则 ①设则②设，是两个可积分的函数，则 第一换元法 设，则 第二换元法 若所求积分为的形式虽不复杂，实际则较难求解．此时，通常作变换把积分化为 的形式，如果右端的不定积分比较容易计算，那么最后将结果中的变量还原，将 代入结果．定积分的概念 定积分的基本公式 ，则，这个公式叫做积分基本公式又叫牛顿—莱布尼茨公式 定积分的性质 ① ② ③ 微 定 积 定积分的换元积分法 积 分 分 初 步 定积分的分部积分法 函数，在区间上有连续的一阶导数，，有 分段函数的积分 奇偶函数与周期函数的定积分 ①为偶函数 ②为奇函数 若是一个以为周期的连续函数，对任意，有；；导数的几何意义定义的应用 单调性与函数 设函数在闭区间上连续，在开区间上可微，在内，若恒有，则在闭区间上严格单 调上升；若恒有，则在闭区间上严格单调下降． 极值与导数 导 数 求最值 与 微 导 用微分法描述函数图像的一般步骤 分 数 的 和 应 微分的应用 微 用 对于函数，当自变量有增量，函数就有增量，即．一般的说，只要函数的对应法则 积 稍微复杂一点儿，依赖于的情况很复杂，因此对于给定的和，要计算的精确值是 分 很困难的，通常以一个值（微分）代替，这就是微分的本质．其应用形式是或 的 应 用 曲线的渐近线方程 ①若，则渐近线为；②若，则渐近线为③若，，，则函数图像有斜渐近线 不定积分的应用 积 分 定积分在几何上的应用 的 常用于计算平面图形的面积、旋转体的体积等等． 应 用 定积分在力学上的应用 常用于计算变速直线运动的路程、变力做功等等． 定积分在经济生活中的应用 常用于计算供需函数、消费者剩余和生产者剩余等等．复数的三角形式的概念 三角形式与代数形式的转化 任何一个复数都可以表示成的形式。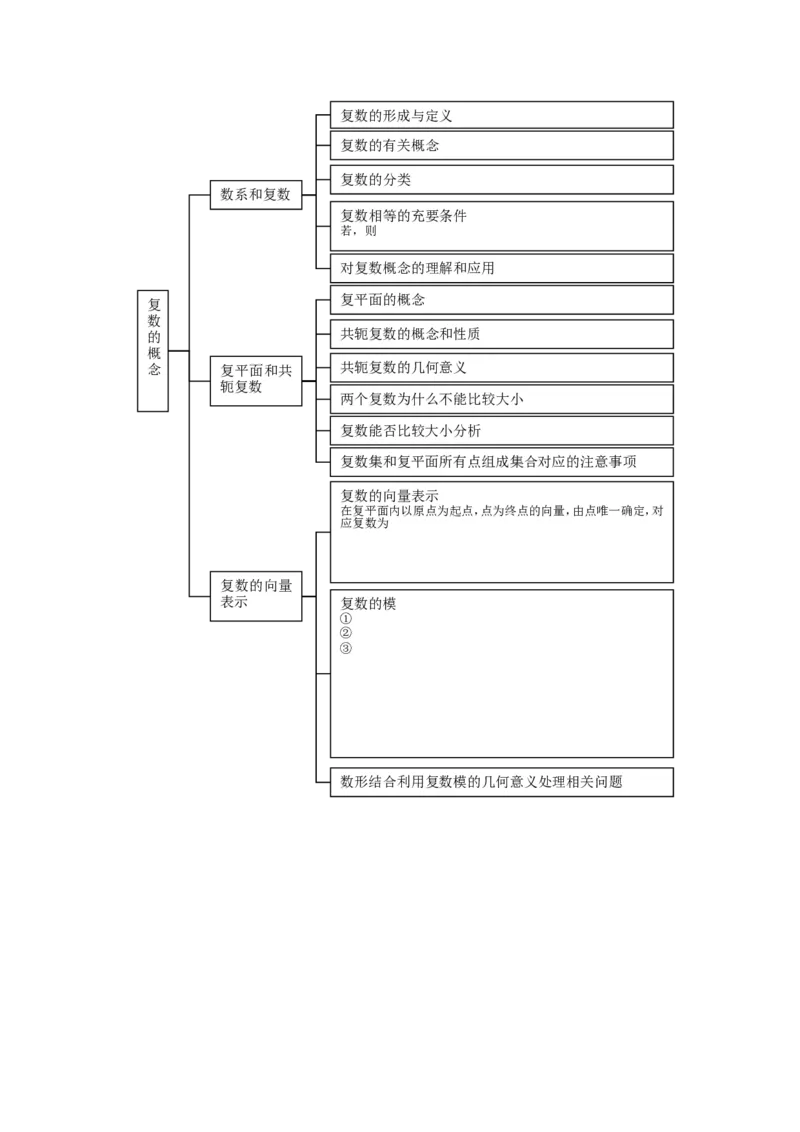其中 ，为复数的幅角，r为复数z的模 复数的 三角形 复数的乘除法和乘方开方 式及其 ①若 复 运算 则； 数 的 ② r(cosθ ＋ isinθ)n ， {cos[(θ ＋ 2kπ)/n] ＋ isin[(θ ＋ 三 2kπ)/n]} (k＝1，2，…，n－1)其中； 角 形 式 和 几 何 形 式 复数加 复数的三角形式的正确表示 减乘除 法、乘 复数加减法的几何意义 方、开 方运算 的几何 复平面上的曲线方程 意义 复数乘除法的几何意义 复数运算的几何意义的应用数系和复数 复数的概念 复平面和共轭复数 复数的向量表示 复数的四则运算和性质 复数的运算与复数域方程 复数域方程 复数 复数的三角形式及其运算 复数的三角形式和几何形式 复数加减乘除法与乘方、开 方运算的几何意义 复数的应用 复数的应用 复数的加减法 两个复数的和 复数的加法满足交换律、结合律，即对任意的有：（交换律） （结合律） 复数的四则 运算和性质 复 复数的乘除法 数 的 运 算 与 复 数 域 方 程 ω，i的幂运算周期性 ，； 。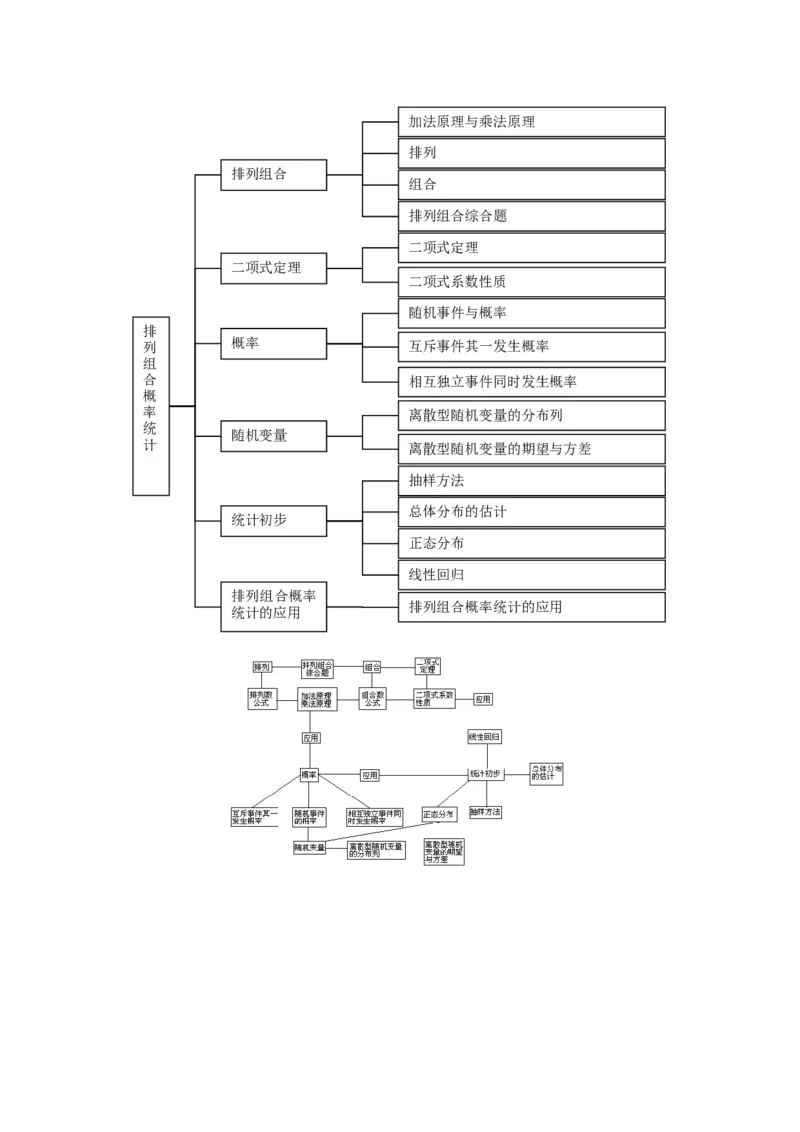 复数域方程 虚实相互转化 含有z的复数方程与解法复数的形成与定义 复数的有关概念 复数的分类 数系和复数 复数相等的充要条件 若，则 对复数概念的理解和应用 复平面的概念 复 数 的 共轭复数的概念和性质 概 念 复平面和共 共轭复数的几何意义 轭复数 两个复数为什么不能比较大小 复数能否比较大小分析 复数集和复平面所有点组成集合对应的注意事项 复数的向量表示 在复平面内以原点为起点，点为终点的向量，由点唯一确定，对 应复数为 复数的向量 表示 复数的模 ① ② ③ 数形结合利用复数模的几何意义处理相关问题加法原理与乘法原理 排列 排列组合 组合 排列组合综合题 二项式定理 二项式定理 二项式系数性质 随机事件与概率 排 列 概率 互斥事件其一发生概率 组 合 相互独立事件同时发生概率 概 率 离散型随机变量的分布列 统 随机变量 计 离散型随机变量的期望与方差 抽样方法 总体分布的估计 统计初步 正态分布 线性回归 排列组合概率 排列组合概率统计的应用 统计的应用加法原理 加 法 原 理 乘法原理 与 乘 法 原 分类计数与分步计数 理 怎样分类和分步 排列 排列数 排列数公式 排列数恒等式 排列 以及 排 怎么理解排列定义中的一定顺序 列 组 怎样理解排列数和加法原理、乘法原理的关系 合 组合 组合数 组合数公式 组合 组合数恒等式 、、、 . 区别排列和组合 组合应用题的解题思路 枚举法 排除法 排 列 组 合 插空法 综 合 捆绑法 题 对称法 集合法二项式定理 通项公式 的第项，记作 两种特殊的表达 二 项 式 定 的展开式通项 理 的系数是 二 项 式 正确理解二项式系数和项的系数的差别 定 理 怎样用二项式定理求近似值 怎样用二项式定理求解余数问题 性质一 二 性质二 项 式 性质三 系 数 性 质 性质四 杨辉三角 怎样求展开式中系数最大的项必然事件、不可能事件、随机事件 随 机 事 一次试验 件 与 概 率 概率的定义 概率公式 互斥事件 两个事件的发生概率为两互斥事件可以用概率加法公式 概 互 斥 事 率 件 其 一 发 生 概 率 对立事件 对立事件概率满足，但反之未必成立. 对立事件和互斥事件的关系 相互独立事件同时发生概率 个独立事件同时发生的概率，等于每个事件发生的概率的积.即 相 互 独 立 事 件 同 时 发 生概率 独立重复试验的事件概率 如果在1次试验中某事件发生的概率是，那么在次重复独立事件中 这个事件恰好发生k次的概率是随机变量 离 散 离散型随机变量 型 随 离散型随机变量的分布列 机 变 分布列的性质 量 的 二项分布 分 布 列 超几何分布 期望的含义 随 为随机变量的期望或者均值 机 变 量 方差的含义 为的均方误差，简称方差 离 散 型 标准差 随 叫做的标准差 机 变 量 随机变量的线性函数的期望和方差 的 若是离散型随机变量，则，其中a，b是常数，也是离散型随机变量，而且， 期 望 和 方 差 服从二项分布的随机变量的期望与方差公式 设，令，那么统计初步 简单随机抽样及其特点 系统抽样及其特点 分层抽样及其特点 抽样分布 三种抽样方法的等概率性 三种抽样方法比较 总体分布的估计 总体分布的 离散型总体及其频率分布表示法 估计 连续型总体及其频率表示法 总体与总体分布 统计初步 频率分布和总体分布的关系 累计分布曲线和累计频率分布 密度曲线与密度函数 正态分布 正态分布及其参数的含义 正态曲线及其性质 函数以及函数 利用求随机变量位于某区间的概率 变量之间的关系 相关关系 排列组合概 率统计的应 散点图 用 回归分析 线性回归分析的思想以及回归直线方程 相关系数和相关性检验平面的性质 平面 平面两直线的位置关系 空间两直线的位置关系 直线与直线的关系 两条异面直线所成角 直线与直线平行 直 线 直线和平面平行 与 直线与平面的关系 平 面 直线和平面所成角 平面和平面平行 二面角 几何中的平行关系和特 征角 异面直线上两点间距离 直线与平面的应用 直线与平面的应用面 面是没有厚度而只有位置和大小的几何图形 平面 可看成是由一条直线沿同一方向平行移动的轨迹 平面图形和空间图形 平面图形可看作是空间图形的一部分 平面的表示法 平面常用一个小写希腊字母表示，或用平面上的多边形的顶点字母表示 平 面 的 斜二测画法规则 定 义 从直线和平面的类比来理解平面 和 表 平面几何与立体几何的联系与区别 示 法 斜二测画法的本质与实际应用 平面的基本性质 平 平面的基本性质实际上就是关于平面的三个公理 面 公理1：若，则 公理2：若，则且 公理3：若，则A、B、C共面 平面基本性质的推论 这几个推论都是公理3的推论 。 平面的性质及推论的用途 平 性质1注药用语判定直线在平面内 面 性质2主要用来判断两面相交 的 性质3和推论都是确定一个平面的依据。 性 质 几何符号语言与常用语言的互化 平面的性质公理与推论的理解和运用平面两条直线的位置关系 平面两 平行公理及其推论 直线的 ①若，则b和c重合 ②若，b和c不重合，则 位置关 系 点到直线的距离 平面上两条直线的距离 异面直线的定义 空间两条直线的位置关系 空间两 直线的 异面直线的判定方法 位置关 系 是否强调共面 怎样理解数学元素间的距离 空间两条直线所成角 空间直线垂直 两条异面直线所成的角 直 线 两条异 两条异面直线垂直 与 直 面直线 线 的 所成的 异面直线的公垂线和公垂线段 关系 角 异面直线的距离 对异面直线所成的角的深度理解 相交直线和异面直线的比较 几何中的角度问题 对异面直线所成的角的深度理解 三线平行公理 射线的平行、正平行与逆平行 直线与 等角定理及推论 直线平 行 空间两条直线平行的判定方法 几何中的平行关系与特征角 升维思想与降维思想直线和平面平行 直线和平面的位置关系 直线和平面平行的判定定理 直 线 与 平 面 平 直线和平面平行的性质定理 行 空间直线和平面平行的判定方法 特征角 升维思想与降维思想 直线和平面垂直 直线和平面的垂足 直 线 直线和平面垂直的判定定理 与 平 面 垂 直 线 直 直线和平面垂直的性质定理 与 平 面 的 关系 点到平面的距离 异面直线上两点的距离公式 直 线 射影 和 平 面 所 直线和平面斜交 成 的 角 直线和平面所成的角 最小角定理 三垂线定理 若与H，，则 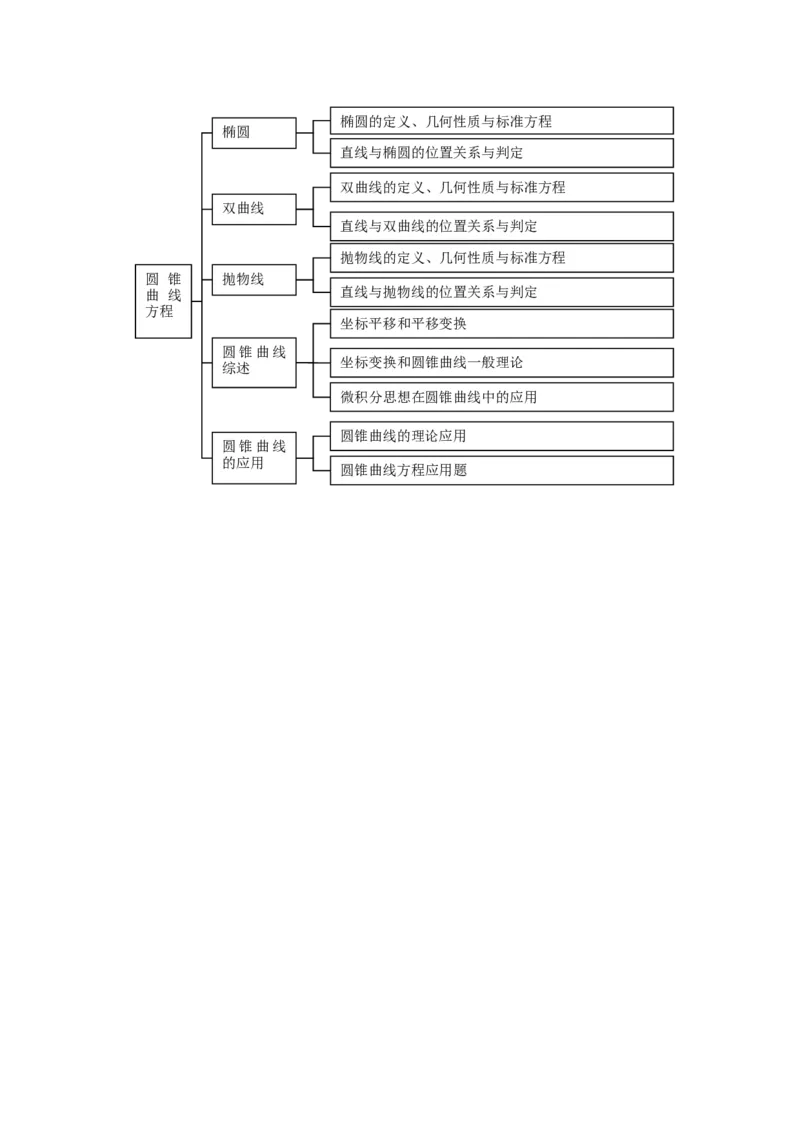空间直线垂直的判定方法椭圆的定义、几何性质与标准方程 椭圆 直线与椭圆的位置关系与判定 双曲线的定义、几何性质与标准方程 双曲线 直线与双曲线的位置关系与判定 抛物线的定义、几何性质与标准方程 圆 锥 抛物线 曲 线 直线与抛物线的位置关系与判定 方程 坐标平移和平移变换 圆锥曲线 坐标变换和圆锥曲线一般理论 综述 微积分思想在圆锥曲线中的应用 圆锥曲线的理论应用 圆锥曲线 的应用 圆锥曲线方程应用题椭圆的定义 ①普通定义：F1 、F2 ，a∈R，且2a＞|F 1 F 2 |，|MF 1 |+|MF 2 |=2a点M∈椭圆F 1 F 2 ②第二定义：F，l，e∈R，且F l，0＜e＜1，d为动点M到直线l的距离，| MF|/d=e点M∈椭圆F上 椭圆定义的延伸 椭 圆 的 定 椭圆的标准方程 义 、 焦点在x轴上：；焦点在y轴上： 几 何 性 质 与 标 准 方 程 椭圆的几何性质 椭圆的参数方程 的参数方程 椭圆的焦三角形面积公式 连接椭圆的两个焦点和椭圆上一点的三角形的面积为 椭 圆 直线和椭圆的位置关系 椭圆的切线 椭 圆 ①在点处的切线方程为 ②直线与椭圆相切的条件为 和 直 ③过椭圆外点引两条切线,切点弦所在的直线方程为 线 的 位 置 关系 直线与椭圆所成的弦长问题 椭圆的弦的中点问题 椭圆的共轭直径双曲线的定义 ①普通定义：F1 、F2 ，a∈R，且2a＞|F 1 F 2 |，|MF 1 |+|MF 2 |=2a点M∈椭圆F 1 F 2 ②第二定义：F，l，e∈R，且F l，0＜e＜1，d为动点M到直线l的距离，| MF|/d=e点M∈椭圆F上 椭圆定义的延伸 双 曲 线 的 椭圆的标准方程 定 焦点在x轴上：；焦点在y轴上： 义 、 几 何 性 质 与 标 准 方 椭圆的几何性质 程 椭圆的参数方程 的参数方程 椭圆的焦三角形面积公式 双 连接椭圆的两个焦点和椭圆上一点的三角形的面积为 曲 线 直线和椭圆的位置关系 椭圆的切线 ①在点处的切线方程为 双 曲 ②直线与椭圆相切的条件为 线 和 ③过椭圆外点引两条切线,切点弦所在的直线方程为 直 线 的 位 置 关 系 直线与椭圆所成的弦长问题 椭圆的弦的中点问题 椭圆的共轭直径抛物线的定义 F l，d为动点M到直线l 的距离，|MF|/d=e=1点M∈抛物线F 抛物 线的 定 抛物线的标准方程 义、 焦点在x轴正半轴上：；在x轴负正半轴上： 几何 焦点在y轴正半轴上：；在y轴负正半轴上： 性质 与标 准方 程 抛物线的几何性质 抛物线的参数方程 抛物线的参数方程为. 抛 物 线 直线和抛物线的位置关系 抛物线的切线 抛物 ①上一点的切线方程为 线和 ②直线与抛物线相切的条件为 直线 ③过抛物线外一点引切线，切点弦所在的直线方程为 的位 ④过切点与此点处切线垂直的直线称为抛物线的法线.过抛物线上一点作平行于 置关 对称轴的一条射线（射线方向为抛物线开口方向），则此时经过该点的法线平分过 系 这一点的焦半径与此射线的夹角. 直线与抛物线所成的弦长问题 抛物线的弦的中点问题 抛物线的升华公式坐标轴平移公式 坐标轴平移公式的应用 利用坐标轴平移公式化简二元二次方程 长短轴平行于坐标轴的任意中心的椭圆方程 长轴平行于x轴; 长轴平行于y轴： 坐 标 平 圆 移 锥 和 曲 平 线 移 综 虚实轴平行于坐标轴的任意中心的双曲线方程 变 述 实轴平行于x轴： 换 实轴平行于y轴： 对称轴平行于坐标轴的任意顶点的抛物线方程 对称轴平行于x轴，开口向右： 对称轴平行于x轴，开口向左： 对称轴平行于y轴，开口向上： 对称轴平行于y轴，开口向下： 给定渐近线的双曲线系方程 坐标轴平移和图像平移 图像平移公式 图像平移公式的应用 如何理解平移公式中的左加右减、上加下减坐标轴旋转公式 坐标变换 坐标轴旋转公式的应用 和圆锥曲 线的一般 利用坐标轴旋转公式化简二元二次方程 理论 基本的对称变换 关于经过原点的直线的对称变换 圆 锥 极坐标下圆锥曲线的参数方程 曲 线 综述 圆锥曲线系 对称公式的进一步补充 关于任意点的旋转变换 经过两圆锥曲线的交点的圆锥曲线系 一般二次曲线切线问题的常规解法 坐标变换 一般二次曲线切线问题的微积分解法 和圆锥曲 线的一般 一般二次曲线切点弦问题的常规解法 理论 一般二次曲线切点弦问题的微积分解法 直线与圆锥曲线相切与直线与圆锥曲线有一个交点 过定点作与双曲线相交于一点的直线问题