文档内容
淮滨县多校联考 2023-2024 学年下期期末考试
高一数学试卷
注意事项:
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。考试时间120分钟,满分150分。
考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。交卷
时只交答题卡。
第I卷(选择题,共58分)
一、选择题(本题共8小题,每小题5分,共40分。每小题给出的四个选项中,只有一个
选项是正确的,请把正确的选项填涂在答题卡相应的位置上。)
1.已知集合 ,则 ( )
A. B. C. D.
2.已知复数 满足 ,则复数 的虚部为( )
A. B. C. D.
3.设A,B是直线l上两点,则“A,B到平面a的距离相等”是“ ”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既
不充分也不必要条件
4.若样本数据 的方差为 ,则 的方差为( )
A. B. C. D.
5.已知 是 的中线, ,以 为基底表示 ,则 ( )
A. B.
C. D.
6.已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l ⊥m,l ⊥n, 则
( )
A.α∥β且 ∥α B.α⊥β且 ⊥β
C.α与β相交,且交线垂直于 D.α与β相交,且交线平行于
7.如图,已知边长为4的正方形ABCD的中心与半径为 的圆O的圆心重合,点P是圆
第 1 页 共 10 页
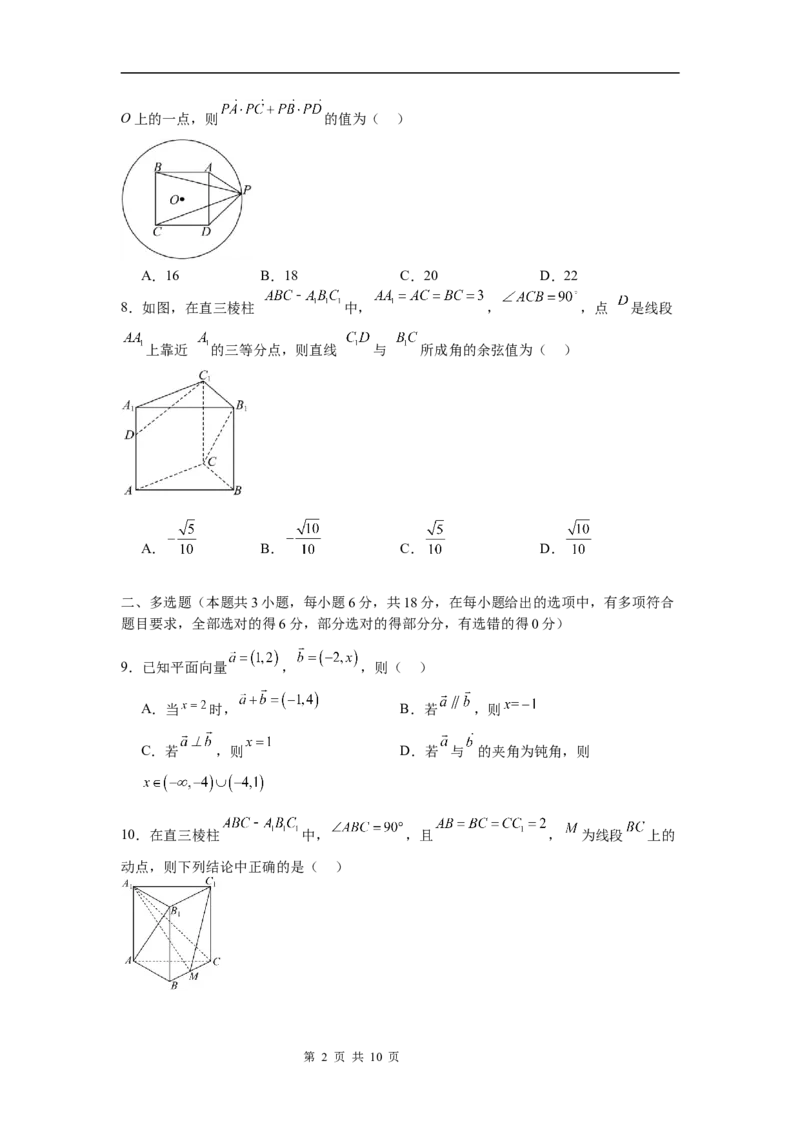
学科网(北京)股份有限公司O上的一点,则 的值为( )
A.16 B.18 C.20 D.22
8.如图,在直三棱柱 中, , ,点 是线段
上靠近 的三等分点,则直线 与 所成角的余弦值为( )
A. B. C. D.
二、多选题(本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合
题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.已知平面向量 , ,则( )
A.当 时, B.若 ,则
C.若 ,则 D.若 与 的夹角为钝角,则
10.在直三棱柱 中, ,且 , 为线段 上的
动点,则下列结论中正确的是( )
第 2 页 共 10 页A.
B.异面直线 与 所成角的取值范围为
C. 的最小值为
D.当 是 的中点时,过 三点的平面截三棱柱 外接球所得的
截面面积为
11.设 为随机事件,且 ,下列说法正确的是( )
A.事件 相互独立与 互斥不可能同时成立
B.若三个事件 两两独立,则
C.若事件 独立,则
D.若 ,则
第II卷(非选择题,共92分)
三、填空题(本题共3小题,每小题5分,共计15分)
12.已知水平放置的四边形 的斜二测直观图为矩形 ,已知 ,
,则四边形 的周长为 .
13.如图,已知正三棱柱 的底面边长为 ,高为 ,一质点自 点出
发,沿着三棱柱的侧面绕行一周到达 点的最短路线的长为 .
14.某市半程马拉松比赛需要学生志愿者若干名,其中某路段从某校高一年级1000人中按
男、女采用比例分配的分层随机抽样抽取一个容量为50的样本,且样本中男生人数比女生
人数多20人,则这1000人中女生有 人.
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
第 3 页 共 10 页
学科网(北京)股份有限公司15.(13分)设复数 (其中 ), .
(1)若 是实数,求 的值;
(2)若 是纯虚数,求 .
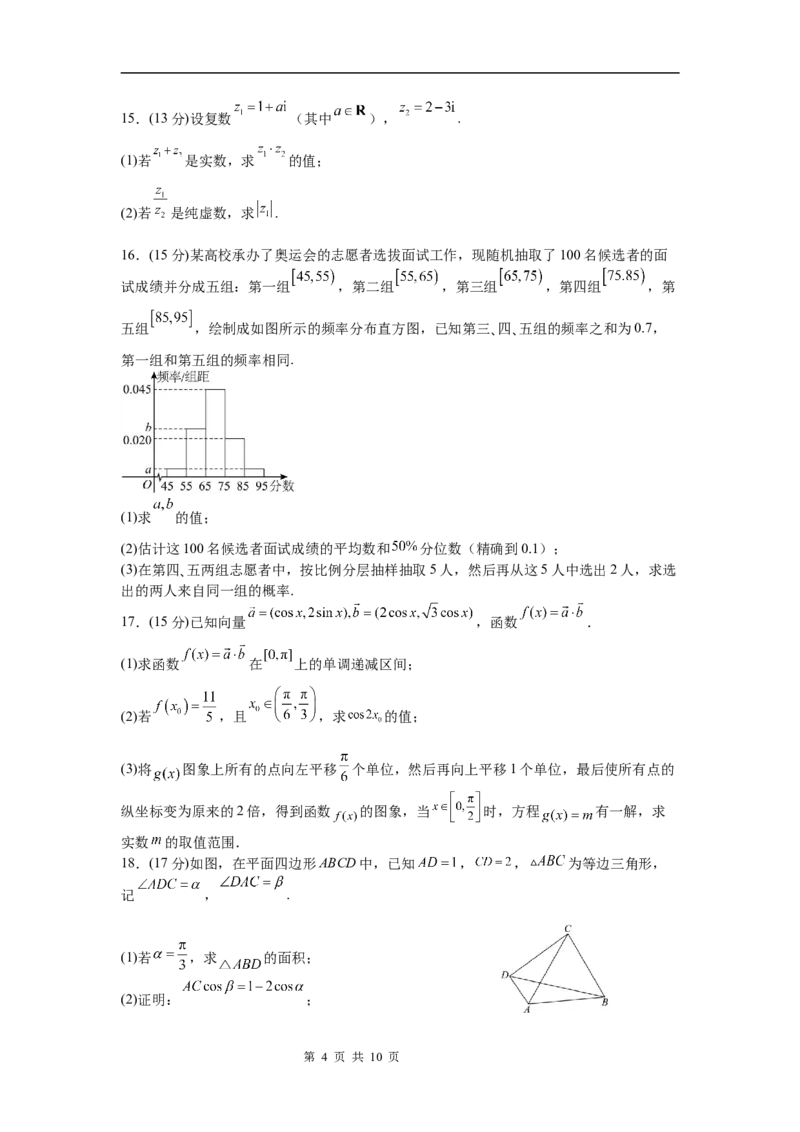
16.(15分)某高校承办了奥运会的志愿者选拔面试工作,现随机抽取了100名候选者的面
试成绩并分成五组:第一组 ,第二组 ,第三组 ,第四组 ,第
五组 ,绘制成如图所示的频率分布直方图,已知第三、四、五组的频率之和为0.7,
第一组和第五组的频率相同.
(1)求 的值;
(2)估计这100名候选者面试成绩的平均数和 分位数(精确到0.1);
(3)在第四、五两组志愿者中,按比例分层抽样抽取5人,然后再从这5人中选出2人,求选
出的两人来自同一组的概率.
17.(15分)已知向量 ,函数 .
(1)求函数 在 上的单调递减区间;
(2)若 ,且 ,求 的值;
(3)将 图象上所有的点向左平移 个单位,然后再向上平移1个单位,最后使所有点的
纵坐标变为原来的2倍,得到函数 的图象,当 时,方程 有一解,求
实数 的取值范围.
18.(17分)如图,在平面四边形ABCD中,已知 , , 为等边三角形,
记 , .
(1)若 ,求 的面积;
(2)证明: ;
第 4 页 共 10 页(3)若 ,求 的面积的取值范围.
19.(17分)如图1,在矩形 中, 是线段 上(包括端点)的
一动点,如图2,将 沿着 折起,使点 到达点 的位置,满足点 平面
.
(1)如图2,当 时,点 是线段 上点的, 平面 ,求 的值;
(2)如图2,若点 在平面 内的射影 落在线段 上.
①是否存在点 ,使得 平面 ,若存在,求 的长;若不存在,请说明理
由;
②当三棱锥 的体积最大值时,求点 到平面 的距离
淮滨县多校联考 2023-2024 学年下期期末考试
高一数学参考答案
第I卷(选择题,共58分)
一、选择题(本题共8小题,每小题5分,共40分。)
1 2 3 4 5 6 7 8
D A B C B D C C
二、多选题(本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合
题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9 10 11
ACD ABD ACD
第II卷(非选择题,共92分)
三、填空题(本题共3小题,每小题5分,共计15分)
12. 10
13.
14.300
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(1)由已知 ,
第 5 页 共 10 页
学科网(北京)股份有限公司是实数,
,即 ,
.(6分)
(2) ,
由于 是纯虚数, ,解得 ,
则 .
.(7分)
16.(1)因为第三、四、五组的频率之和为0.7,
所以 ,解得 ,
所以前两组的频率之和为 ,即 ,解得 ;(3分)
(2)由(1)知,
平均数为 ;
前两组频率之和为0.3,前三组频率之和为0.75,所以中位数位于 组内,
且 ,即 分位数为69.4;(5分)
(3)第四、五两组志愿者分别有20人, 人,
故按照分层抽样抽得第四组志愿者人数为4,分别设为
第五组志愿者人数为1,设为 ,
这5人选出2人,所有情况有
,共10种,
其中选出的2人来自同一组的有 ,共6种,
所以选出的2人来自同一组的概率为 .(7分)
17.(1)因为
,
所以 即
第 6 页 共 10 页又因为 ,所以函数 在 上的单调递减区间为 (3分)
(2)若 则 ,所以 .
因为 ,所以 ,
所以 ,
所以
故 .(6分)
(3)将 图象上所有的点的纵坐标变为原来的 ,再向下平移1个单
位,最后再向右平移 个单位得到函数 的图象,
即:
则 ,
当 时,
由方程 有一解,可得 的取值范围为 .(7分)
18.(1)在平面四边形 中,已知 , , 为等边三角形,记
,
在 中,由余弦定理, ,
所以 ,则 ,所以 ,
又因为 为等边三角形,
所以 ,且 ,
第 7 页 共 10 页
学科网(北京)股份有限公司所以 ,
则 的面积为 ;(4分)
(2)在 中,由正弦定理可得 ,
即 且 ,
由于 ,
故 ,
由于三角形中, ,因此 ,得证,(6分)
(3)在平面四边形 中,已知 , , 为等边三角形, ,
设 ,
在 中,由余弦定理,
,
,
在 中,由正弦定理, ,即 ,所以
,
结合
,
又因为 ,所以 ,
所以 ,
即 的面积的取值范围为 .(7分)
19.(1)取 的中点 ,连接 ,
因为 ,所以 ,
因为 ∥ ,所以四边形 为平行四边形,
所以 ∥ ,
因为 平面 , 平面 ,
所以 ∥平面 ,
第 8 页 共 10 页因为 ∥平面 , , 平面 ,
所以平面 ∥平面 ,
因为平面 平面 ,平面 平面 ,
所以 ∥ ,
因为 是 的中点,所以 ;(6分)
(2)①存在点 ,当点 与点 重合,即 时, 平面 ,
理由如下:当点 与点 重合时,则 ,
因为 平面 , 平面 ,所以 ,
因为 , 平面 ,
所以 平面 ,
因为 平面 ,所以 ,
因为 , , 平面 ,
所以 平面 ,
即当点 与点 重合, 时, 平面 ;(4分)
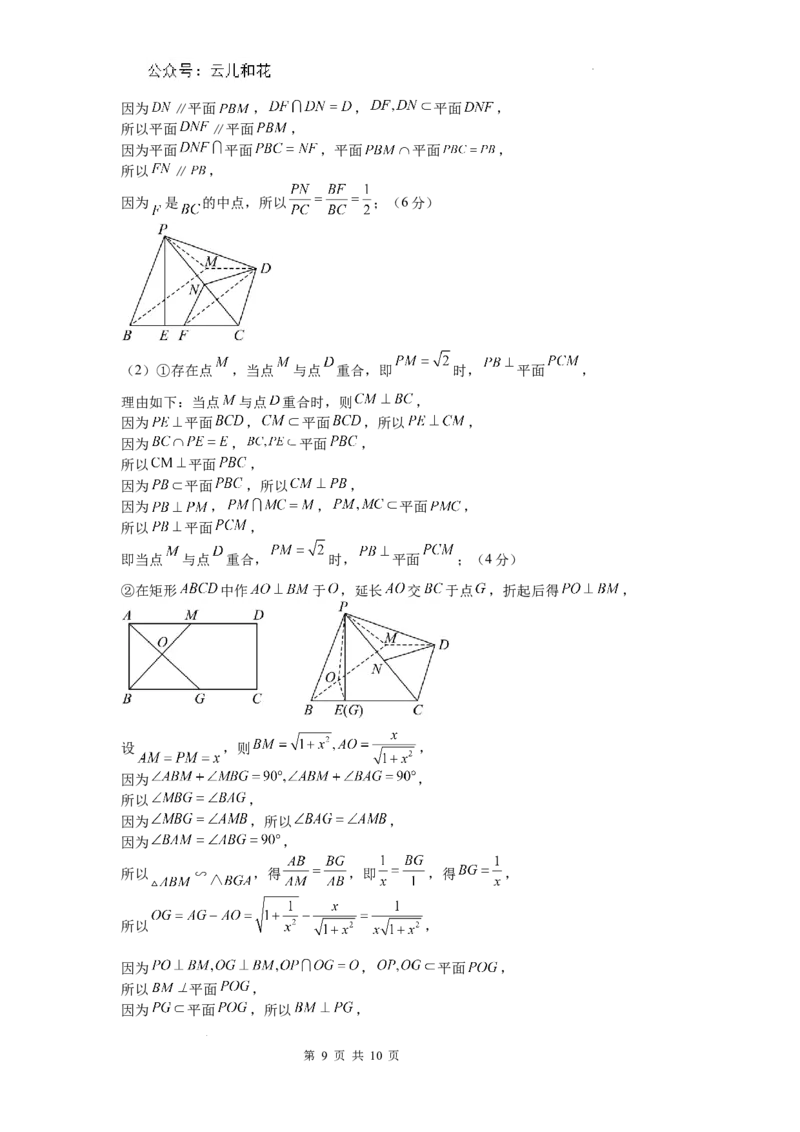
②在矩形 中作 于 ,延长 交 于点 ,折起后得 ,
设 ,则 ,
因为 ,
所以 ,
因为 ,所以 ,
因为 ,
所以 ∽ ,得 ,即 ,得 ,
所以 ,
因为 , 平面 ,
所以 平面 ,
因为 平面 ,所以 ,
第 9 页 共 10 页
学科网(北京)股份有限公司因为 平面 , 平面 ,所以 ,
所以点 与点 重合,
因为要使得点 的射影落在线段 上,所以 ,
则 ,解得 ,
在 中, ,
所以
,
当且仅当 ,即 时, ,
当 时, , ,则 是 的中点,
所以点 到平面 的距离为 .(7分)
第 10 页 共 10 页