四川省凉山州2024届高中毕业班高三年级第三次诊断性检测(凉山三诊)文科数学试卷答案(1)_2024年5月_025月合集_2024届四川省凉山州高三第三次诊断性检测(凉山三诊)

凉山州第三次诊断性考试文科数学参考答案
一，选择题（每题5分，共60分）：
1-5：BDADB 6-10：CCAAC 11-12：CC
12题解析：令x y 0 f(0)0,x y 1 f(1)0， ①对；
f(x) x x
x  x (0,),g(x)  g(xy) g(x)g(y)，g(x ) g(x  2) g(x )g( 2)
1 2 x 2 1 x 1 x
1 1
x
f( 2)
x x
 g(x )g(x ) g( 2) 1 0②对；当x0时由①知③成立，当x0时，由
2 1 x x
1 2
x
1
②g(xn) g(x)g(xn1) g(xn)g(xn1) g(x) g(xn) g(x)(n1)g(x)
f(xn) f(x)
ng(x) n  f(xn)nxn1f(x)
xn x 所以③正确.
1 1
由①得 f(2)2f( ) f(1)0 f(2)2由③得
2 2
f(xn) f(2n) n f(2i) n
 xn1f(x) 2n1 f(2) 2i1f(2)2n12得④错.
n n i
i1 i1
二，填空题（每题5分，共20分）
3 3 3 3 4
13.【答案】1 14.【答案】3 15【答案】(  , ] 16【答案】
2 2 2 3
             1
2
16题解析：OGBC (AGAO)(AC AB)  AGAC AGABAO(AC AB)  AC
2
1 2 1     1 4
 AB  (AC AB)(AC AB) 4 (91)
2 3 3 3
三，解答题（共70分，17题10分，18-22每题12分）
17.解：根据扇形统计图易得选择物理类学生为1000(48%24%18%)900人，其中
8 7
男生900 480人，女生900 420，选择历史类100人，其中男生
15 15
2 3
100 40人，女生100 60人
5 5
男生 女生 合计
物理类 480 420 900
历史类 40 60 100
合计 520 480 1000....................................................................................................................................................3分
n(ad bc)2 1000(4806042040)2 250
K2    6.4106.635
(ab)(cd)(ac)(bd) 900100520480 39
所以没有99%把握认为“该校学生选择物理类与性别有关”.................................6分
(2) 记“至少有一名男生被抽到”为事件M,按照性别分层抽样抽取5人，则抽到男生2名，
记作A,B，女生3名，记作C,D,E .从5人中随机抽取2人，共：{A,B},{A,C},
{A,D},{A,E},{B,C},{B,D}, {B,E},{C,D},{C,E},{D,E}10种不同取法，事件M
发生包含：{A,B},{A,C},{A,D},{A,E},{B,C},{B,D},{B,E}共7个基本事件，
7 7
由古典概型得P(M )  ，所以至少有1名男生被抽到的概率为 ................12分.
10 10
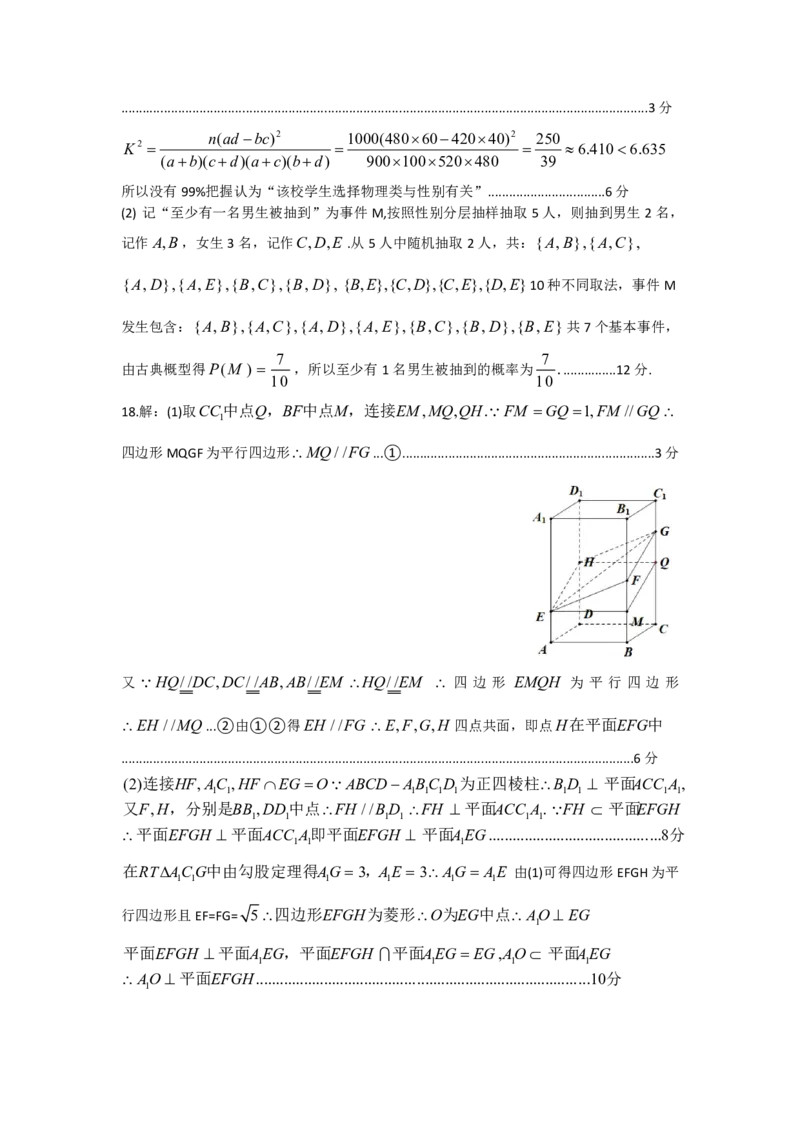
18.解：(1)取CC中点Q，BF中点M，连接EM,MQ,QH.FM GQ 1,FM //GQ
1
四边形MQGF为平行四边形MQ//FG...①.......................................................................3分
又 HQ//DC,DC//AB,AB//EM HQ//EM  四 边 形 EMQH 为 平 行 四 边 形
EH //MQ ...②由①②得EH //FGE,F,G,H 四点共面，即点H在平面EFG中
................................................................................................................................................6分
(2)连接HF,AC ,HF EG OABCDABC D 为正四棱柱BD  平面ACC A,
1 1 1 1 1 1 1 1 1 1
又F,H，分别是BB ,DD中点FH //BD FH  平面ACC A.FH  平面EFGH
1 1 1 1 1 1
平面EFGH  平面ACC A即平面EFGH  平面AEG...........................................8分
1 1 1
在RTACG中由勾股定理得AG  3，AE  3AG  AE 由(1)可得四边形EFGH为平
1 1 1 1 1 1
行四边形且EF=FG= 5四边形EFGH为菱形O为EG中点AO EG
1
平面EFGH 平面AEG，平面EFGH 平面AEG EG,AO  平面AEG
1 1 1 1
AO平面EFGH...................................................................................10分
1在RTEOH中，OH  2,EH  5OE  EH 2OH 2  3
1
S  EGHF  2 6
EFGH 2
在RTEOA中，AE  3,OE  3AO  AE2OE2  6
1 1 1 1
1
V  S AO  4......................................................12分
A 1 EFGH 3 EFGH 1
1 3 2
解：（1）第一个等边三角形顶点坐标B ( a , a )代入 y  x 得a  ，将点
1 2 1 2 1 1 3
1 3 4 1 3
B(a a, a)坐标代入y  x a  ,将点B (a a  a , a )坐标代入
2 1 2 2 2 2 2 3 3 1 2 2 3 2 3
8 2
y  x得a  ,a  n ......................................................................................6分
3 3 n 3
（2）由（1）得
1 9 1 9 1 1 1 9 1 1 1 1 1
 T  (  ... ) (1   ...  )
a a 4n(n1) n 4 12 23 n(n1) 4 2 2 3 n n1
n n1
9 1 9n
 (1 )
4 n1 4n4 ........................................................................................................12分
y y y2
20.解:(1)设动点P(x,y),k k   3 x2  1(x 1).................4分
PA 2 PA 1 x1 x1 3
3 3
(2) 易知直线AB斜率不为0.设AB方程为xty2,且t( , ).设A(x ,y ),
3 3 1 1
B(x ,y ).
2 2
 xty2

 y2 (3t2 1)y2 12ty90(3t2 10)
x2  1

 3
12t 9
y  y  ,y y  ， 36(t2 1)0....................6分
1 2 13t2 1 2 13t23(x 1) 3(x 1)
由题意易得k k 3k  2 直线BA方程为y  2 (x1).....①
BA 1 BA 2 BA 1 y 1 y
2 2
y
直线AA 方程为 y  1 (x1)......②............................................................................8分
2 x 1
1
由①②得
9
x1 y y y y y y 13t2
 1 2  1 2  1 2 
x1 3(x 1)(x 1) 3(ty 1)(ty 1) 3(t2y y t(y  y )1) 9t2 12t2
1 2 1 2 1 2 1 2 3(  1)
13t2 13t2
9 1 1
3 x 点M横坐标为定值 ......12分
3(9t2 12t2 13t2) 2 2
备注：非对称式处理方式比较多，此处只提供利用第三定义转化回避非对称式，整体代换，
半配凑，硬解方式处理非对称式均给满分.
1
21.解：(1)当m0时, f '(x) (2x1)ex 0 x  ..............................................2分；
2
1 1
当x(, )时f '(x)0, f(x)单调递减；当x( ,)时f '(x)0, f(x)单调递增...4分
2 2
1
 f(x)极小值点是- ,无极大值点.....................................................................6分.
2
1
(2)f '(x) (2x1)(exm) 0 x  或lnm
2
e
当m 时, f '(x) 0,函数f (x)单调递增，至多一个零点，不满足条件...7分；
e
e 1 1
当0m 时函数 f(x)在(,lnm)单调递增,(lnm,- )单调递减，( ,)
e 2 2
单调递增, f(lnm)mlnm(1lnm)0，函数 f(x)至多一个零点，不满足..................8分
e 1 1
当m 时，函数 f(x)在(,- )单调递增,(- ,ln m)单调递减，(ln m,) 单调递增.
e 2 2
f(5)11e5 19m0, 令 g(x)ex x1,g'(x)ex 10 x 0g(x) 在区间
(,0)单调递减，(0,)单调递增，g(x) g(0)0ex x1 ex1  xex ex
即
x e e2 e2
e2  xex  x2.f (m) (2m1)emm3m2m (2m1) m2m3m2m
2 4 4e2 e2 5
m[( 1)m2( 1)m1)m( m23m1)0...............................10分
2 4 2
 1 5m 2  8 e
f( )  0  m 8 e
 2 4 e  5e   m1或m e
5e
 
f(lnm)mlnm(1lnm)0 0m1或me
8 e
综上： m的取值范围是( ,1)(e,) .....................................................................12 分
5e
（若用极限说明：x，f (x)0;x, f (x)0，扣1分）
22.解：(1)由2  x2  y2,cos x,sin y ,则C为
4 22 cos2sin2  22cos2,C 的极坐标方程为2 2cos2,
由题意易得直线l的极坐标方程为,R....................................4分
(2)
由题意得=0时 2即M(- 2,0),N( 2,0)
1
直线l过原点S  |MN |y  2y ,
MNP 2 P P
，
2 2cos2 2 2
联立C,l方程

，且cos
 3
,
则 2cos2 2  2cos21   14
3
14 1 14
又y sin   ，且MN 2 2
P 3 3 9
1 14 2 7
所以S   2 2 ........................................10分
MNP 2 9 9
1
23.解:(1) f(x) 12x  2x  12x2x 1 当0 x 时取“=”a 1..........5分
2
1 8 1 16 1 1 16
(2)法一：由(1)可知a 1，原式     (  )(2x22x)
2x 1x 2x 22x 2 2x 22x
1 1x 16x 1 25 1x 16x 1
(17  ) (172 16) ,当   x (0,1)时取"".
2 x 1x 2 2 x 1x 5
10
分
法二：由柯西不等式得2 2
1 1 16 1 1 16 2 2 (14)2 25
原式 (  )(2x22x) (  )( 2x  22x ) 
2 2x 22x 2 2x 22x 2 2
1 2 1
当且仅当   x 时取""..........................10分
2x 1x 5
法三:由权方和不等式得
12 42 (14)2 25 1 4 1
原式    ,当   x 时取" ".......10分
2x 22x 2x22x 2 2x 22x 5