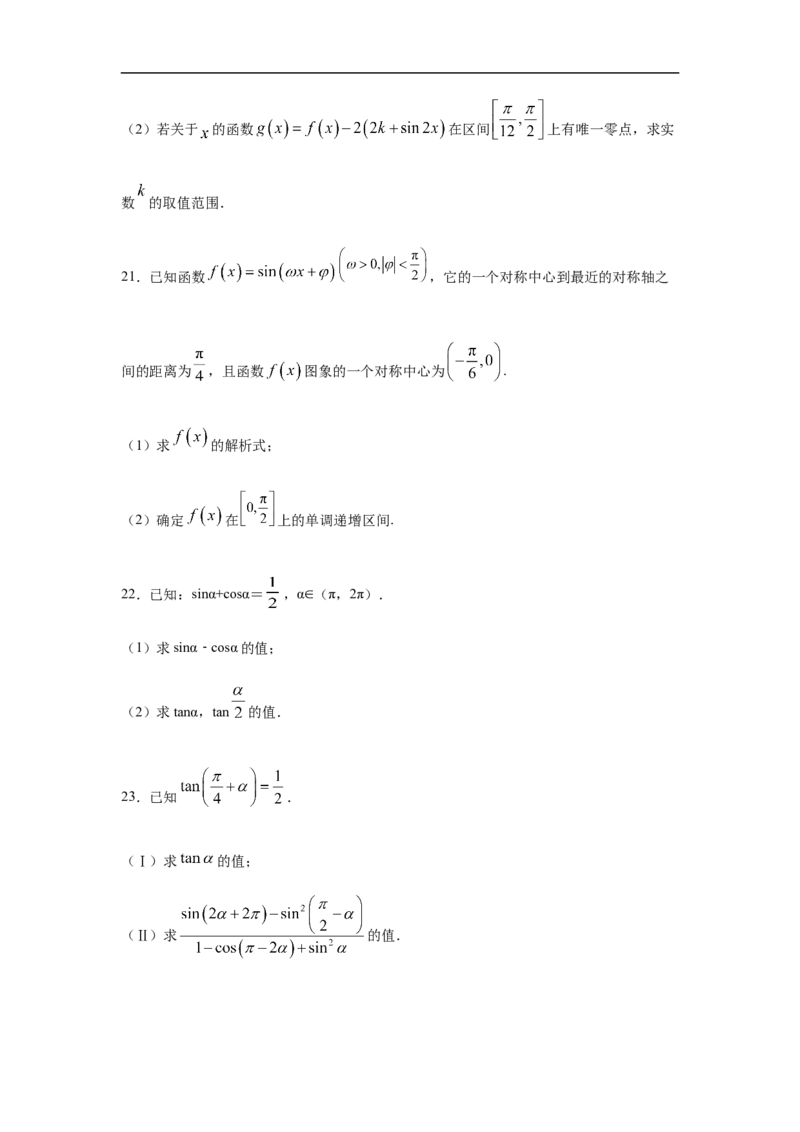文档内容
第5单元 三角函数(强化篇)
基础知识讲解
一.运用诱导公式化简求值
【基础知识】
利用诱导公式化简求值的思路
1.“负化正”,运用公式三将任意负角的三角函数化为任意正角的三角函数.
2.“大化小”,利用公式一将大于360°的角的三角函数化为0°到360°的三角函数,利用
公式二将大于180°的角的三角函数化为0°到180°的三角函数.
3.“小化锐”,利用公式六将大于90°的角化为0°到90°的角的三角函数.
4.“锐求值”,得到0°到90°的三角函数后,若是特殊角直接求得,若是非特殊角可由计
算器求得.
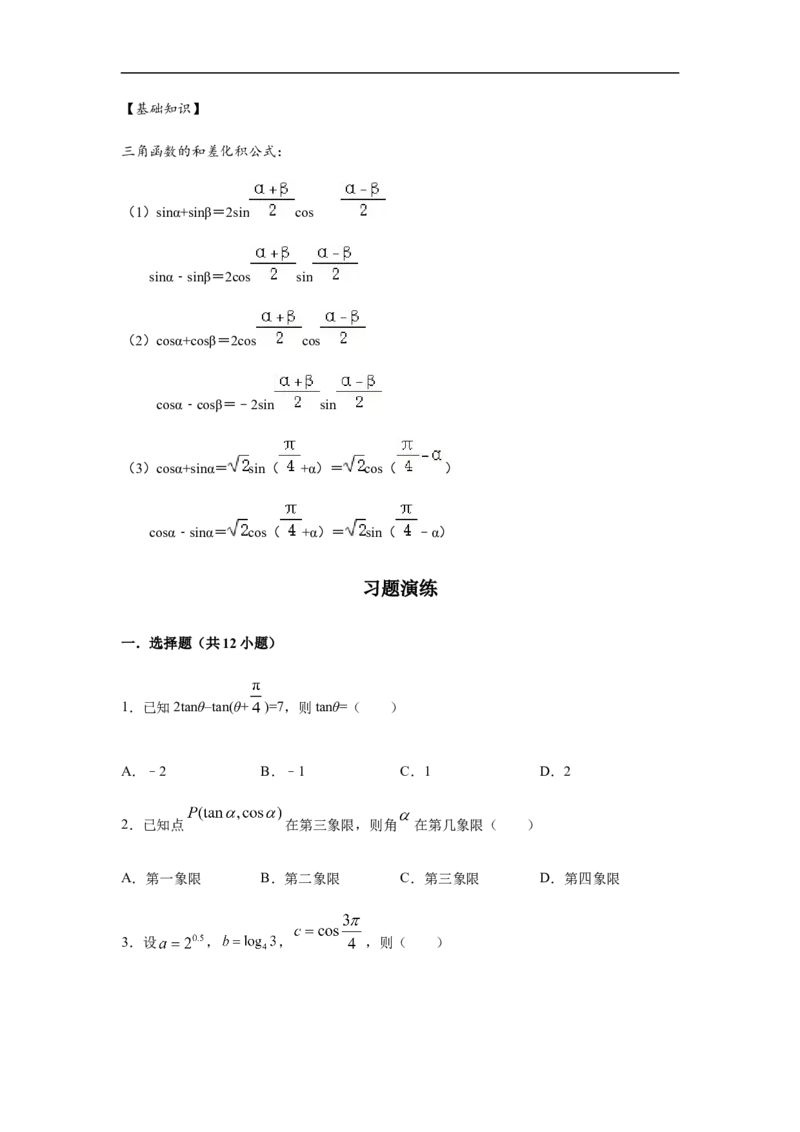
二.正弦函数、余弦函数、正切函数的图象和性质
函数 y=sin x y=cos x y=tan x
图象
定义域 R R k∈Z
值域 [﹣1,1] [﹣1,1] R
单调性 递增区间: 递增区间: 递增区间:(2kπ﹣π,2kπ)
(k∈Z);
(2kπ﹣ ,2kπ+ ) (kπ﹣ ,kπ+ )
递减区间:
(k∈Z); (k∈Z)
(2kπ,2kπ+π)
递减区间:
(k∈Z)
(2kπ+ ,2kπ+ )
(k∈Z)
最 值 x=2kπ(k∈Z)时,y
max
无最值
x=2kπ+ (k∈Z)时, =1;
y =1;
max
x=2kπ+π(k∈Z) 时,
x=2kπ﹣ (k∈Z)时, y min =﹣1
y =﹣1
min
奇偶性 奇函数 偶函数 奇函数
对称性 对称中心:(kπ,0)
(k∈Z) 对称中心:(kπ+ , 对称中心:( ,0)
0)(k∈Z) (k∈Z)
对称轴:x=kπ+ ,k∈Z 对称轴:x=kπ,k∈Z 无对称轴
周期 2π 2π π
三.同角三角函数间的基本关系
【基础知识】
1.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
(2)商数关系: =tanα.2.诱导公式
公式一:sin(α+2kπ)=sin α,cos(α+2kπ)=cos_α,其中k∈Z.
公式二:sin(π+α)= ﹣ si n_α,cos(π+α)= ﹣ co s_α,tan(π+α)=tan α.
公式三:sin(﹣α)= ﹣ si n_α,cos(﹣α)=cos_α.
公式四:sin(π﹣α)=sin α,cos(π﹣α)= ﹣ co s_α.
公式五:sin( ﹣α)=cosα,cos( ﹣α)=sinα.
公式六:sin( +α)= cos α ,cos( +α)= ﹣ si n α
3.两角和与差的正弦、余弦、正切公式
(1)cos (α﹣β)= cos α cos β + sin α sin β ;
(2)cos(α+β)= cos α cos β ﹣ sin α sin β ;
(3)sin(α+β)= sin α cos β + cos α sin β ;
(4)sin(α﹣β)= sin α cos β ﹣ cos α sin β ;
(5)tan(α+β)= .
(6)tan(α﹣β)= .
4.二倍角的正弦、余弦、正切公式
(1)sin 2α=2sin_ α cos _α;
(2)cos 2α= cos 2 α ﹣sin 2 α = 2cos 2 α ﹣1 = 1﹣2sin 2 α ;
(3)tan 2α= .
【技巧方法】诱导公式记忆口诀:
对于角“ ± ”(k Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,“奇
变偶不变”是指“α当k为奇∈数时,正弦变余弦,余弦变正弦;当 k为偶数时,函数名不
变”.“符号看象限”是指“在 的三角函数值前面加上当 为锐角时,原函数值的符
号”. α α
四.两角和与差的三角函数
【基础知识】
(1)cos (α﹣β)=cosαcosβ+sinαsinβ;
(2)cos(α+β)=cosαcosβ﹣sinαsinβ;
(3)sin(α+β)=sinαcosβ+cosαsinβ;
(4)sin(α﹣β)=sinαcosβ﹣cosαsinβ;
(5)tan(α+β)= .
(6)tan(α﹣β)= .
五.二倍角的三角函数
【基础知识】
二倍角的正弦其实属于正弦函数和差化积里面的一个特例,即α=β的一种特例,其公式为:
sin2α=2sinα•cosα;其可拓展为1+sin2α=(sinα+cosα)2.
二倍角的余弦其实属于余弦函数和差化积里面的一个特例,即α=β的一种特例,其公式为:
cos2α=cos2α﹣sin2α=2cos2α﹣1=1﹣2sin2α.
二倍角的正切其实属于正切函数和差化积里面的一个特例,即α=β的一种特例,其公式为:
tan2α= .对于这个公式要求是能够正确的运用其求值化简即可.六.半角的三角函数
【基础知识】
半角的三角函数关系主要是指正切函数与正余弦函数之间的关系(正余弦的半角关系
其实就是二倍角关系),其公式为:①tan = = = ;
②tan = = = .
七.三角函数的积化和差公式
【基础知识】
三角函数的积化和差公式:
(1)sinαsinβ= [cos(α﹣β)﹣cos(α+β)]
cosαcosβ= [cos(α﹣β)+cos(α+β)]
(2)sinαcosβ= [sin(α+β)+sin(α﹣β)]
cosαsinβ= [sin(α+β)﹣sin(α﹣β)]
(3)tanαtanβ=
tanαcotβ= .
八.三角函数的和差化积公式【基础知识】
三角函数的和差化积公式:
(1)sinα+sinβ=2sin cos
sinα﹣sinβ=2cos sin
(2)cosα+cosβ=2cos cos
cosα﹣cosβ=﹣2sin sin
(3)cosα+sinα= sin( +α)= cos( )
cosα﹣sinα= cos( +α)= sin( ﹣α)
习题演练
一.选择题(共12小题)
1.已知2tanθ–tan(θ+ )=7,则tanθ=( )
A.–2 B.–1 C.1 D.2
2.已知点 在第三象限,则角 在第几象限( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.设 , , ,则( )A. B. C. D.
4.已知 , , 、 ,则 的值为
( )
A. B.
C. D.
5.关于函数 有下述四个结论:
①f(x)是偶函数 ②f(x)在区间( , )单调递增
③f(x)在 有4个零点 ④f(x)的最大值为2
其中所有正确结论的编号是
A.①②④ B.②④ C.①④ D.①③
6.若 ,且 ,则 ( )
A. B. C. D.
7.已知 ,且 ,则 ( )A. B.
C. D.
8.已知函数 的图象与直线 的三个
相邻交点的横坐标分别是2,4,8,则 的单调递减区间是( )
A. , B. ,
C. , D. ,
9.设函数 的定义域为 , , 当 时,
, 则函数 在区间 上的所有零点的和为( )
A. B. C. D.
10.将函数 的图象向右平移 个单位,得到函数
的图象,则函数 的一个极大值点为( )
A. B. C. D.11.函数 ( )的部分图象如图所示,若
,且 ,则 ( )
A.1 B. C. D.
12.已知 , 是方程 的两根,若 ,则
( )
A. B. 或
C. 或 D.
二.填空题(共6小题)
13.已知函数 的图象关于直线 对称,则 的值是
________.
14.已知 ,则 的值是_____.15.若 ,则 __________.
16.已知 ,则 _______.
17. ______.
18.已知函数 ( ),且 ( ),
则 ______.
三.解析题(共6小题)
19.设函数 , .
(1)求 的最小正周期和对称中心;
(2)若函数 的图像向左平移 个单位得到函数 的图像,求函数 在区间
上的值域.
20.已知
(1)求函数 的单调递减区间;(2)若关于 的函数 在区间 上有唯一零点,求实
数 的取值范围.
21.已知函数 ,它的一个对称中心到最近的对称轴之
间的距离为 ,且函数 图象的一个对称中心为 .
(1)求 的解析式;
(2)确定 在 上的单调递增区间.
22.已知:sinα+cosα= ,α∈(π,2π).
(1)求sinα﹣cosα的值;
(2)求tanα,tan 的值.
23.已知 .
(Ⅰ)求 的值;
(Ⅱ)求 的值.24.已知函数 ,其图象与 轴相邻的两个交
点的距离为 .
(1)求函数 的解析式;
(2)若将 的图象向左平移 个长度单位得到函数 的图象恰好经过点
,求当 取得最小值时, 在 上的单调区间.