文档内容
2024-2025 学年浙江省 9+1 联盟高一下学期 4 月期中考试数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合 ,集合 ,则 ( )
A={x|−6B”是“sinA>sinB”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4
4.已知sin(α+β)= ,tanα=3tanβ,则sin(α−β)=( )
5
1 2 1 2
A. B. C. D.
10 5 5 3
5.设a,b∈R,若−1−1
a b
6.已知函数 f(x)= { log 2 x,x≥1 ,若 f(2−a2 )>f(a) ,则实数 a 的取值范围是( )
−x2+2x−1,x<1
A. (−∞,−1)∪(2,+∞) B. (−1,2)
C. (−2,1) D. (−∞,−2)∪(1,+∞)
7.已知函数 是定义在 上的奇函数,当 时, 为常数 ,则 的值为( )
f(x) R x≥0 f(x)=2x+m(m ) f(−log 3)
2
2 2
A. 2 B. −2 C. D. −
3 3
8.已知⃗AB与⃗AC是平面内两个非零向量,|⃗AB|=2,|⃗AC|=3,∠BAC=60∘,点P是∠BAC平分线上
的动点 . 当 P ⃗ A⋅(P ⃗ B+P ⃗ C) 取最小值时, |P ⃗ A| 的值为( )
3√3 5√3 √6 6
A. B. C. D.
5 8 4 5
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
第 页,共 页
1 19.已知向量 ⃗a=(1,2) ,⃗b=(−2,1) ,⃗
c=(3,1)
,则以下说法正确的是( )
A. ⃗
|a|=√5
3 1
B.
⃗在⃗c方向上的投影向量为(
, )
a
2 2
C. ⃗a+⃗b与⃗c垂直
D. 若⃗a+k⃗b与⃗c的夹角为锐角,则k的取值范围是(−∞,1)
10.对于复数z,下列说法正确的是( )
A. 若z2≥0,则z∈R
1
B. 若|z|=1,则z+ ∈R
z
C. 若z3=1,则z=1
D. |z−2+i|表示复平面上z对应的点到点(2,−1)的距离
⃗ ⃗ ⃗
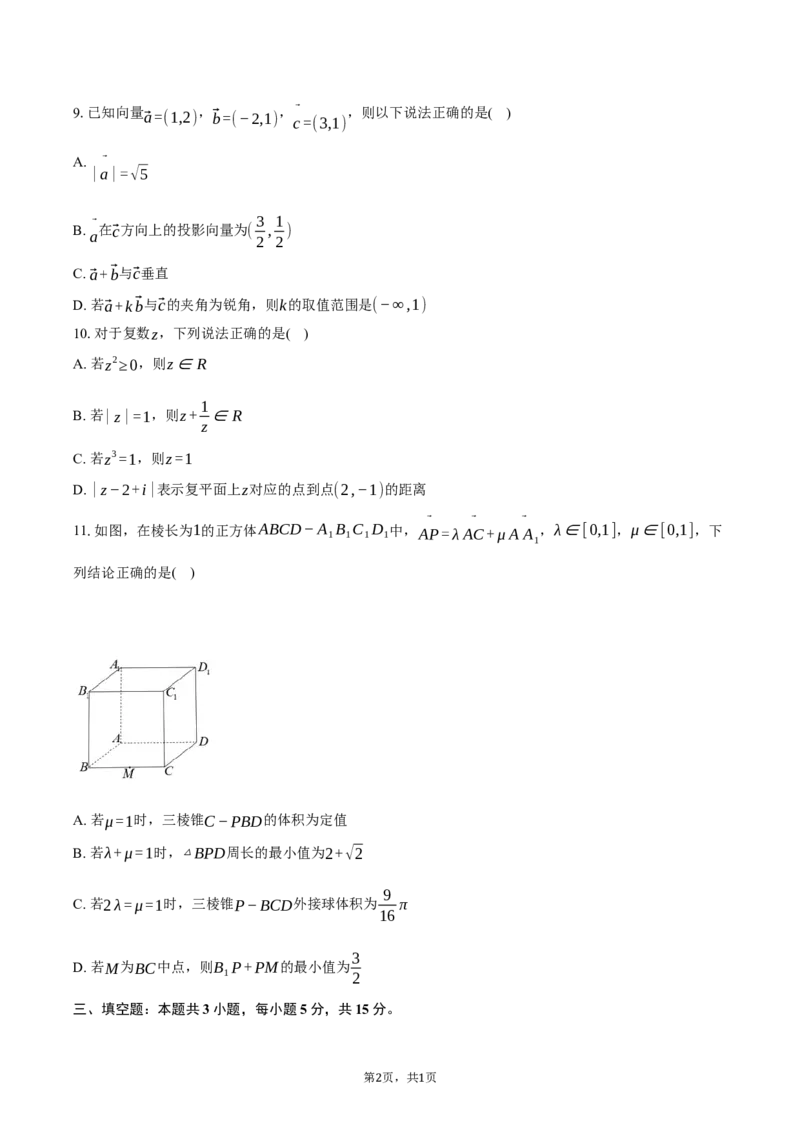
11.如图,在棱长为1的正方体ABCD−A 1 B 1 C 1 D 1 中,AP=λAC+μA A ,λ∈[0,1],μ∈[0,1],下
1
列结论正确的是( )
A. 若μ=1时,三棱锥C−PBD的体积为定值
B. 若λ+μ=1时,△BPD周长的最小值为2+√2
9
C. 若2λ=μ=1时,三棱锥P−BCD外接球体积为 π
16
3
D. 若M为BC中点,则B P+PM的最小值为
1 2
三、填空题:本题共3小题,每小题5分,共15分。
第 页,共 页
2 12 2√3
12.在△ABC中,角A,B,C所对的边分别为a,b,c,A= π,a=2,c= ,则b= .
3 3
13.已知圆锥的母线长为10cm,侧面积为50πcm2,则此圆锥的体积为 cm3.
14.在△ABC中,角A,B,C所对的边分别为a,b,c,若acosB=3bcosA,且b=3,则△ABC面积的
最大值为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知函数f(x)=(log x−1)(log x−3).
2 2
(1)求不等式f(x)≤0的解集A;
(2)若对任意的x∈A,不等式f(x)≥mlog x恒成立,求实数m的取值范围.
2
16.(本小题15分)
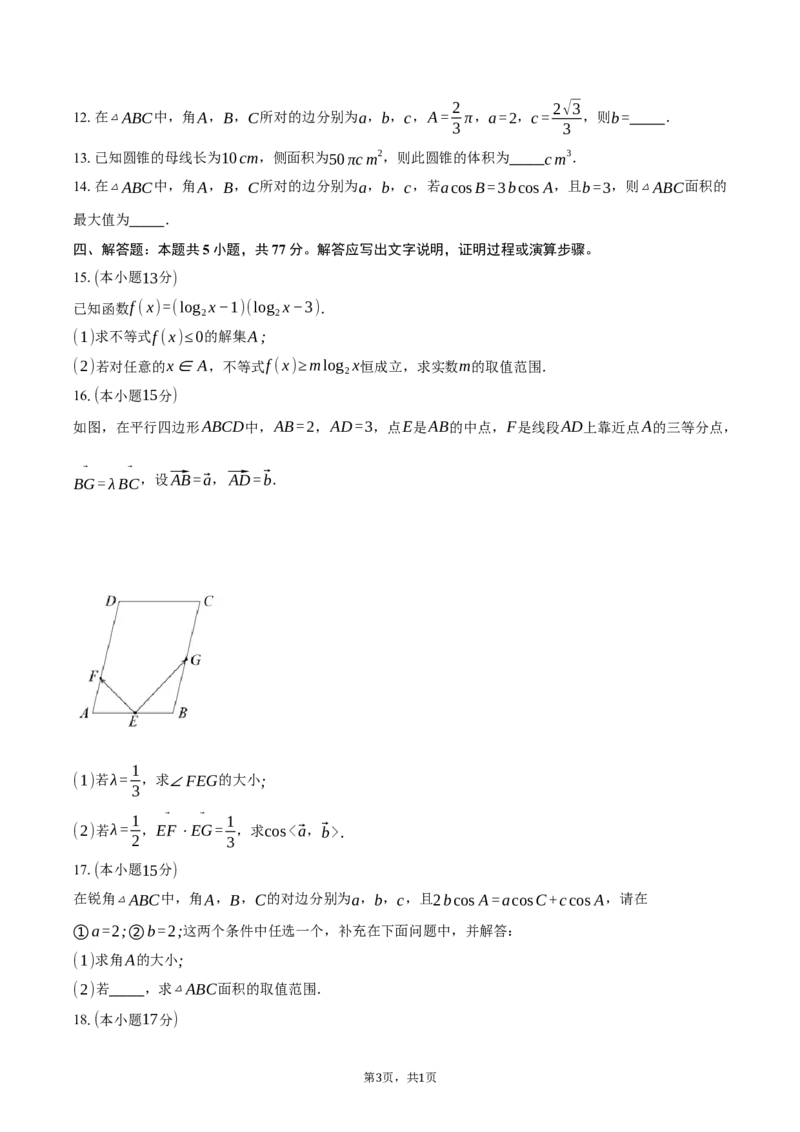
如图,在平行四边形ABCD中,AB=2,AD=3,点E是AB的中点,F是线段AD上靠近点A的三等分点,
⃗ ⃗
BG=λBC
,设⃗AB=⃗a,⃗AD=⃗b.
1
(1)若λ= ,求∠FEG的大小;
3
1 ⃗ ⃗ 1
(2)若λ= ,EF⋅EG= ,求cos<⃗a,⃗b>.
2 3
17.(本小题15分)
在锐角△ABC中,角A,B,C的对边分别为a,b,c,且2bcosA=acosC+ccosA,请在
①a=2;②b=2;这两个条件中任选一个,补充在下面问题中,并解答:
(1)求角A的大小;
(2)若 ,求△ABC面积的取值范围.
18.(本小题17分)
第 页,共 页
3 14
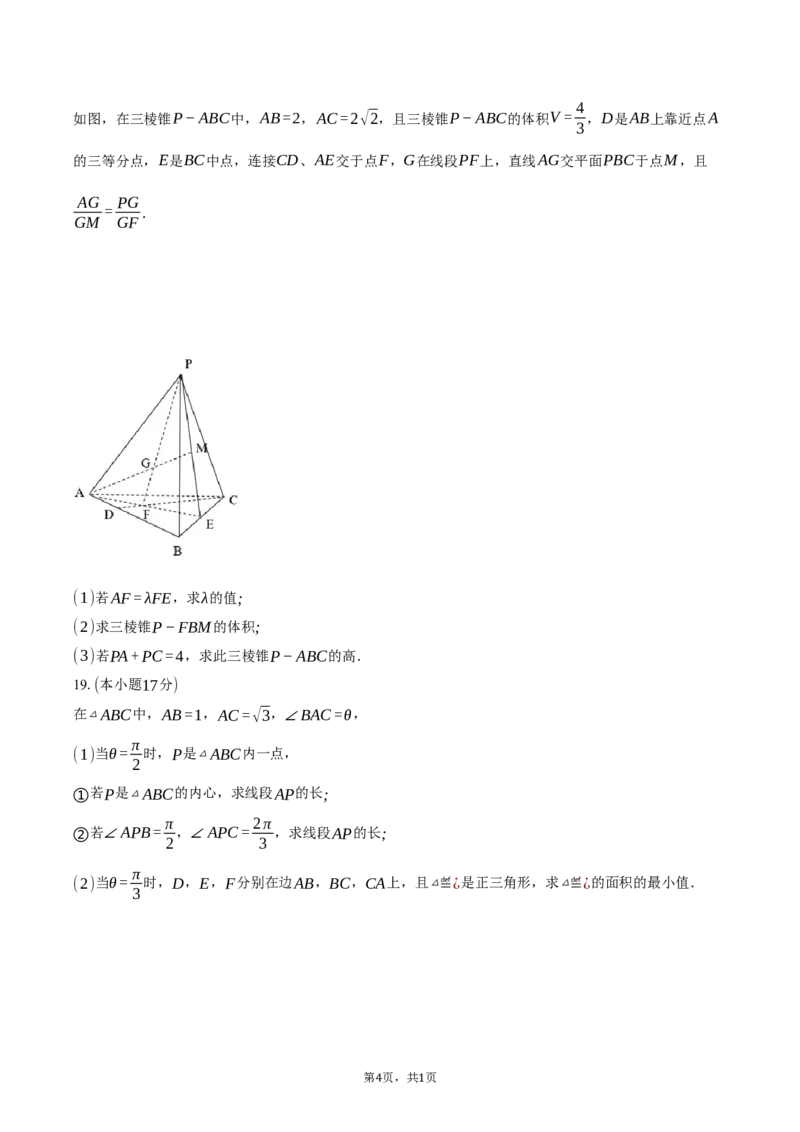
如图,在三棱锥P−ABC中,AB=2,AC=2√2,且三棱锥P−ABC的体积V = ,D是AB上靠近点A
3
的三等分点,E是BC中点,连接CD、AE交于点F,G在线段PF上,直线AG交平面PBC于点M,且
AG PG
= .
GM GF
(1)若AF=λFE,求λ的值;
(2)求三棱锥P−FBM的体积;
(3)若PA+PC=4,求此三棱锥P−ABC的高.
19.(本小题17分)
在△ABC中,AB=1,AC=√3,∠BAC=θ,
π
(1)当θ= 时,P是△ABC内一点,
2
①若P是△ABC的内心,求线段AP的长;
π 2π
②若∠APB= ,∠APC= ,求线段AP的长;
2 3
π
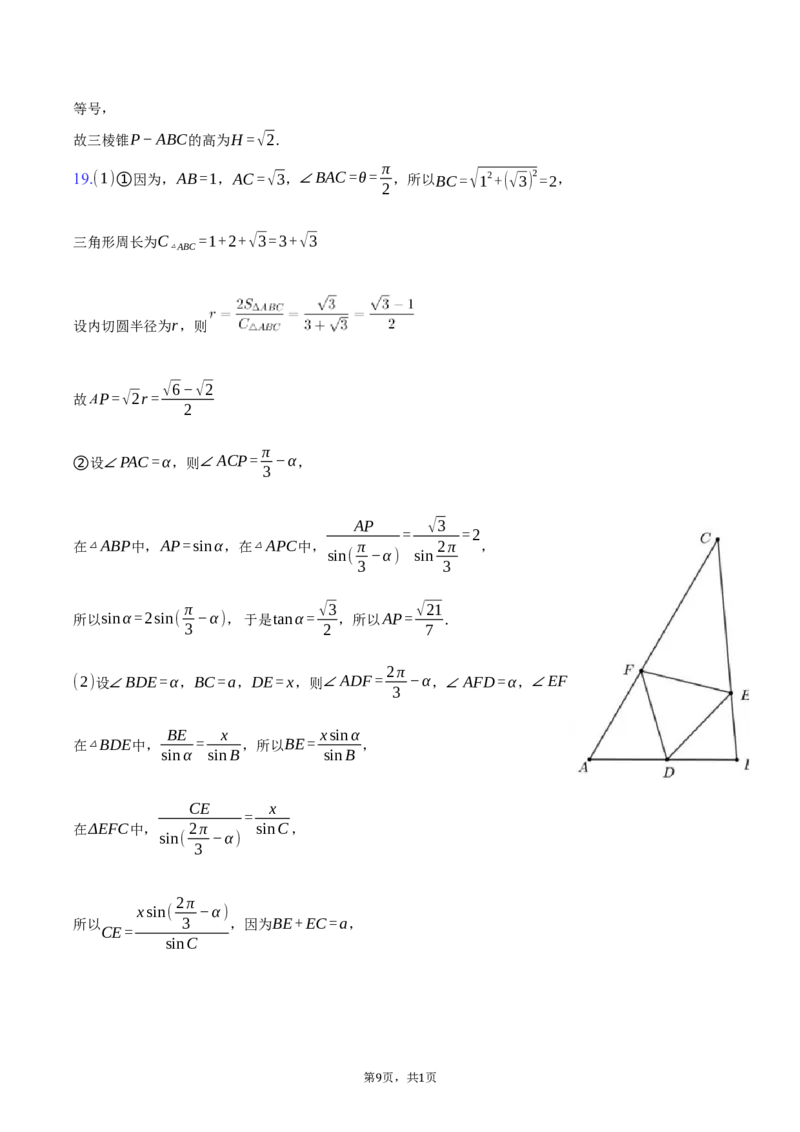
(2)当θ= 时,D,E,F分别在边AB,BC,CA上,且△≝¿是正三角形,求△≝¿的面积的最小值.
3
第 页,共 页
4 1参考答案
1.D
2.A
3.C
4.B
5.D
6.C
7.B
8.B
9.ABC
10.ABD
11.ACD
2√3
12.
3
125√3
13. π
3
14.9
15.解:(1)令t=log x,
2
则原不等式f(x)=(log x−1)(log x−3)⩽0可化为(t−1)(t−3)⩽0,解得1⩽t⩽3,
2 2
即1⩽log x⩽3,
2
所以2⩽x⩽8,
不等式f(x)⩽0的解集为A={x|2⩽x⩽8}.
由题意得: ,
(2) (log x) 2−4log x+3⩾mlog x
2 2 2
3
因为2⩽x⩽8,所以log x+ ⩾m+4
2 log x
2
令t=log x,t∈[1,3].
2
3
原不等式可化为t+ ⩾m+4对于t∈[1,3]能成立,
t
3
因为t+ ⩾2√3,当t=√3时取等号.
t
故2√3⩾m+4,
第 页,共 页
5 1所以m⩽2√3−4,
即m的取值范围是 .
⃗ 1⃗ 1⃗ ⃗ 1⃗ 1⃗
16.解:(1)EF= b− a,EG= a+ b,
3 2 2 3
⃗ ⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1⃗
EF⋅EG=( b− a)⋅( b+ a)= b2− a2=0,
3 2 3 2 9 4
π
故∠FEG= ;
2
⃗ 1⃗ 1⃗ ⃗ 1⃗ 1⃗
(2)EF= b− a,EG= a+ b,
3 2 2 2
⃗ ⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1 ⃗ ⃗ 1⃗ 1
EF⋅EG=( b− a)( b+ a)= b2− a⋅b− a2= ,
3 2 2 2 6 12 4 3
故⃗a⋅⃗b=2,
⃗ ⃗
⃗ a⋅b 2 1
故cos<⃗a,b>= = = .
⃗ ⃗ 2×3 3
|a||b|
17.解:
(1)∵2bcosA=acosC+ccosA⇒2sinBcosA=sin AcosC+sinCcosA⇒2sinBcosA=sin(A+C)⇒2sinBcosA=sinB
1
∵B∈(0,π),∴sinB≠0,∴cosA= ,
2
π
∵A∈(0,π),∴A= ,
3
(2)若选①a=2;
a b c 4√3
由正弦弦定理可知: = = = ,
sin A sinB sinC 3
1 √3 4√3 4√3 2π 4√3 √3 1
S = bcsin A= bc= sinBsinC= sinBsin( −B)= ( sinBcosB+ sin2B)
ΔABC 2 4 3 3 3 3 2 2
4√3 √3 1−cos2B 4√3 1 π 1 2√3 π √3
= ( sin2B+ )= ( sin(2B− )+ )= sin(2B− )+ ,
3 4 4 3 2 6 4 3 6 3
第 页,共 页
6 1π π 2√3
又因为锐角三角形,B∈( , ),故S ∈( ,√3];
6 2 ΔABC 3
若选②b=2,
2π
√6 2√2sin( −B)
由正弦定理可知a= , 2√2sinC 3 ,
sinB c= =
sinB sinB
2
√3sin( π−B)
1 √3 √3 2sinC 3 3 √3,
S = bcsinA= c= = = +
ΔABC 2 2 2 sinB sinB 2tanB 2
π π √3
又因为锐角三角形,B∈( , ),S ∈( ,2√3).
6 2 ΔABC 2
⃗ ⃗ ⃗ 3 ⃗ ⃗ 3
18.解:(1)设BF=xBA+ yBC= xBD+ yBC,∵F,D,C三点共线,故 x+ y=1①
2 2
同理 B ⃗ F=xB ⃗ A+ yB ⃗ C=xB ⃗ A+2yB ⃗ E ,∵A,F,E三点共线,故x+2y=1②,
1 1
由①②可得x= ,y= ,
2 4
⃗ 1 ⃗ 1 ⃗
故BF= BA+ BE,故F为AE中点,故AF=FE,即λ=1;
2 2
(2)连接PE,∵M∈AG,AG⊂平面PAE,∴M∈平面PAE,
又∵M∈平面PBC,且平面PAE∩平面PBC=PE,∴M∈PE,
AG PG
连接MF,在ΔGAP和ΔGMF中, = ,且∠AGP=∠MGF,
GM GF
第 页,共 页
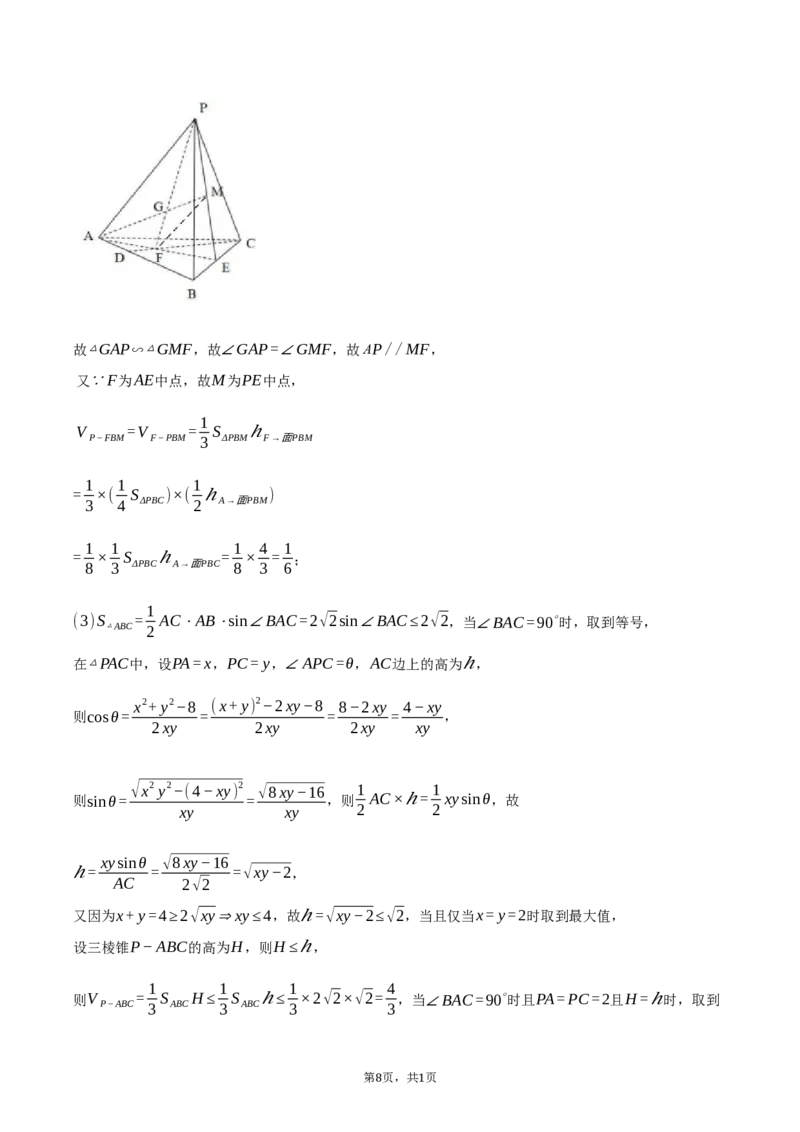
7 1故△GAP∽△GMF,故∠GAP=∠GMF,故AP//MF,
又∵F为AE中点,故M为PE中点,
1
V =V = S ℎ
P−FBM F−PBM 3 ΔPBM F→面PBM
1 1 1
= ×( S )×( ℎ )
3 4 ΔPBC 2 A→面PBM
1 1 1 4 1
= × S ℎ = × = ;
8 3 ΔPBC A→面PBC 8 3 6
1
(3)S = AC⋅AB⋅sin∠BAC=2√2sin∠BAC≤2√2,当∠BAC=90∘时,取到等号,
△ABC 2
在△PAC中,设PA=x,PC= y,∠APC=θ,AC边上的高为ℎ,
x2+ y2−8 (x+ y) 2−2xy−8 8−2xy 4−xy
则cosθ= = = = ,
2xy 2xy 2xy xy
√x2y2−(4−xy) 2 √8xy−16 1 1
则sinθ= = ,则 AC×ℎ = xysinθ,故
xy xy 2 2
xysinθ √8xy−16
ℎ
= = =√xy−2,
AC 2√2
又因为x+ y=4≥2√xy⇒xy≤4,故ℎ =√xy−2≤√2,当且仅当x= y=2时取到最大值,
设三棱锥P−ABC的高为H,则H≤ℎ,
1 1 1 4
则V = S H≤ S ℎ≤ ×2√2×√2= ,当∠BAC=90∘时且PA=PC=2且H= ℎ时,取到
P−ABC 3 ABC 3 ABC 3 3
第 页,共 页
8 1等号,
故三棱锥P−ABC的高为H=√2.
π
19.(1)①因为,AB=1,AC=√3,∠BAC=θ= ,所以BC=√12+(√3) 2=2,
2
三角形周长为C =1+2+√3=3+√3
△ABC
设内切圆半径为r,则
√6−√2
故AP=√2r=
2
π
②设∠PAC=α,则∠ACP= −α,
3
AP √3
= =2
在△ABP中,AP=sinα,在△APC中, π 2π ,
sin( −α) sin
3 3
π √3 √21
所以sinα=2sin( −α), 于是tanα= ,所以AP= .
3 2 7
2π 2π
(2)设∠BDE=α,BC=a,DE=x,则∠ADF= −α,∠AFD=α,∠EFC= −α,
3 3
BE x xsinα
在△BDE中, = ,所以BE= ,
sinα sinB sinB
CE x
=
在ΔEFC中, 2π sinC,
sin( −α)
3
2π
xsin( −α)
所以 3 ,因为BE+EC=a,
CE=
sinC
第 页,共 页
9 11 √3 a
所以 在△ABC中, = = ,
sinC sinB sin A
1 a 1 a
所以 = , = ,
sinB √3sin A sinC sin A
a 1
x= =
所以 2a 2√3a 2π 2 2√3 2π
sinα+ sin( −α) sinα+ sin( −α)
3 3 3 3 3 3
2 2√3 2π 2+√3 √16+4√3
因为 sinα+ sin( −α)= sinα+cosα= sin(α+φ),
3 3 3 3 9
√ 9
所以x≥ ,
16+4√3
9√3
所以ΔDEF面积的最小值为S = .
min 64+16√3
第 页,共 页
10 1