文档内容
2023 学年第二学期期末测试卷
高一数学学科试卷
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.
考试时间120分钟,本次考试不得使用计算器,请考生将所有题目都做在答题卡上.
第Ⅰ卷 (选择题, 共58分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知 ,则 在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 已知向量 则 ( )
A. B. C. D.
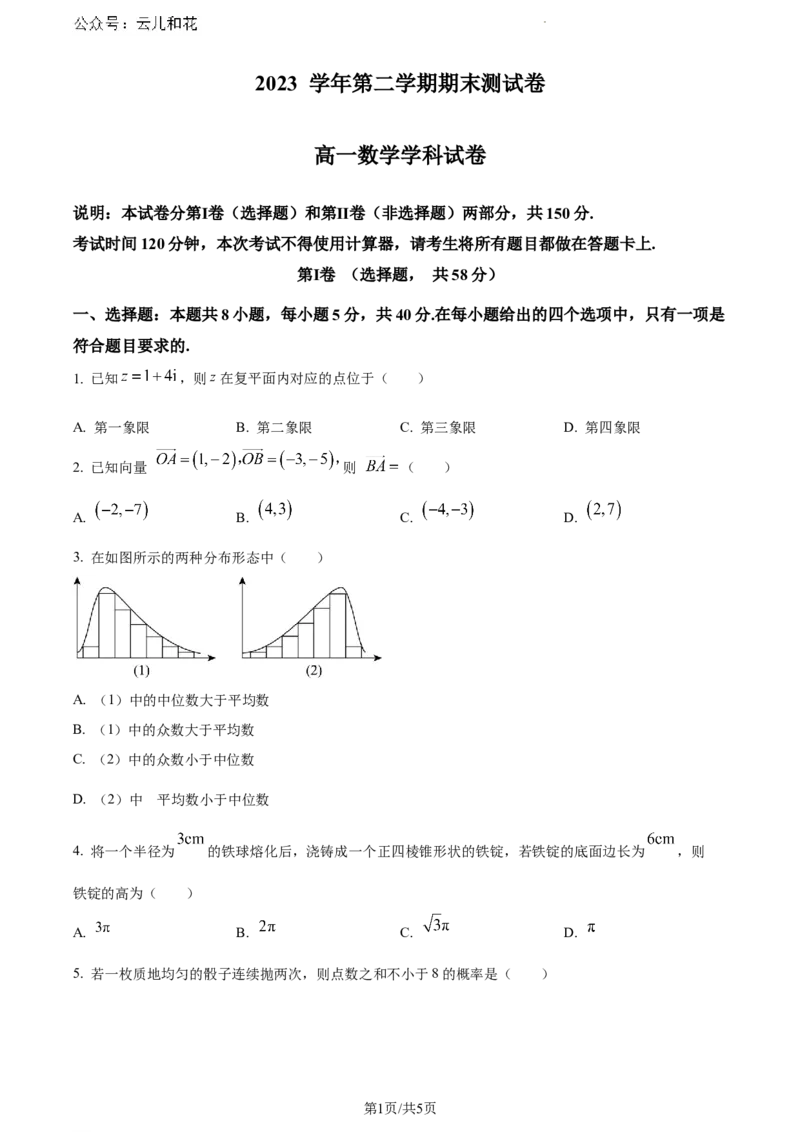
3. 在如图所示的两种分布形态中( )
A. (1)中的中位数大于平均数
B. (1)中的众数大于平均数
C. (2)中的众数小于中位数
的
D. (2)中 平均数小于中位数
4. 将一个半径为 的铁球熔化后,浇铸成一个正四棱锥形状的铁锭,若铁锭的底面边长为 ,则
铁锭的高为( )
A. B. C. D.
5. 若一枚质地均匀的骰子连续抛两次,则点数之和不小于8的概率是( )
第1页/共5页
学科网(北京)股份有限公司A. B. C. D.
6. 在梯形ABCD中, ∥ ,且 ( ),若 则(
)
A. B. C. D.
7. 已知长方体的一条对角线与经过同一个顶点的三个面所成的角分别为 ,若
,则 ( )
A. B. C. D.
8. 在 中,内角A,B,C所对的边分别为a,b,c,若 ,则 的最
大值为( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列命题正确的是( )
A. 若某人打靶时连续射击两次,则事件“至少一次中靶”与“两次都没中靶”是对立事件
B. 若学校田径队有49名运动员,其中男运动员有28人,现按性别进行分层随机抽样,从全体运动员中抽
出一个容量为14的样本,则女运动员应抽取8人
C. 设一组数据的平均数为x,方差为: ,若将这组数据的每一个数都乘以2得到一组新数据,则新数据
的平均数为2x,方差为
D. 设A和B是两个概率大于0的随机事件,若A和B相互独立,则A和B一定不互斥
第2页/共5页
学科网(北京)股份有限公司10. 已知 ,则( )
.
A B.
C. D.
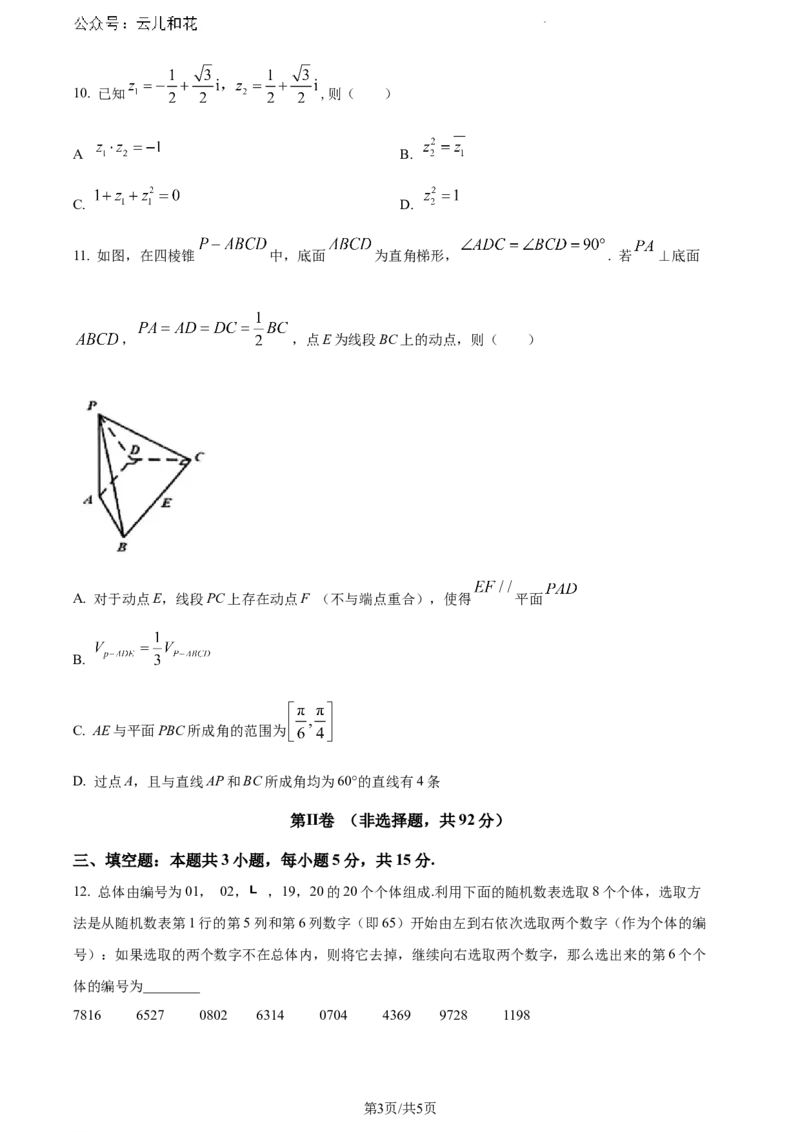
11. 如图,在四棱锥 中,底面 为直角梯形, . 若 ⊥底面
, ,点E为线段BC上的动点,则( )
A. 对于动点E,线段PC上存在动点F (不与端点重合),使得 平面
B.
C. AE与平面PBC所成角的范围为
D. 过点A,且与直线AP和BC所成角均为60°的直线有4条
第Ⅱ卷 (非选择题,共92分)
三、填空题:本题共3小题,每小题5分,共15分.
12. 总体由编号为01, 02, ,19,20的20个个体组成.利用下面的随机数表选取8个个体,选取方
法是从随机数表第1行的第5列和第6列数字(即65)开始由左到右依次选取两个数字(作为个体的编
号):如果选取的两个数字不在总体内,则将它去掉,继续向右选取两个数字,那么选出来的第6个个
体的编号为________
7816 6527 0802 6314 0704 4369 9728 1198
第3页/共5页
学科网(北京)股份有限公司3204 9234 4935 8200 3623 4869 6938 7481
13. 已知海岛 在海岛 的北偏东 的方向上,且两岛的直线距离为 . 一艘海盗船以
的速度沿着北偏东 方向从海岛 出发,同时海警船以 的速度从海岛 进
行追赶,经过 小时后两船相遇,则海警船的航行方向是北偏东_______.
14. 设A,B是一个随机试验中的两个事件,记 为事件A,B的对立事件,且
,则 =__________
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
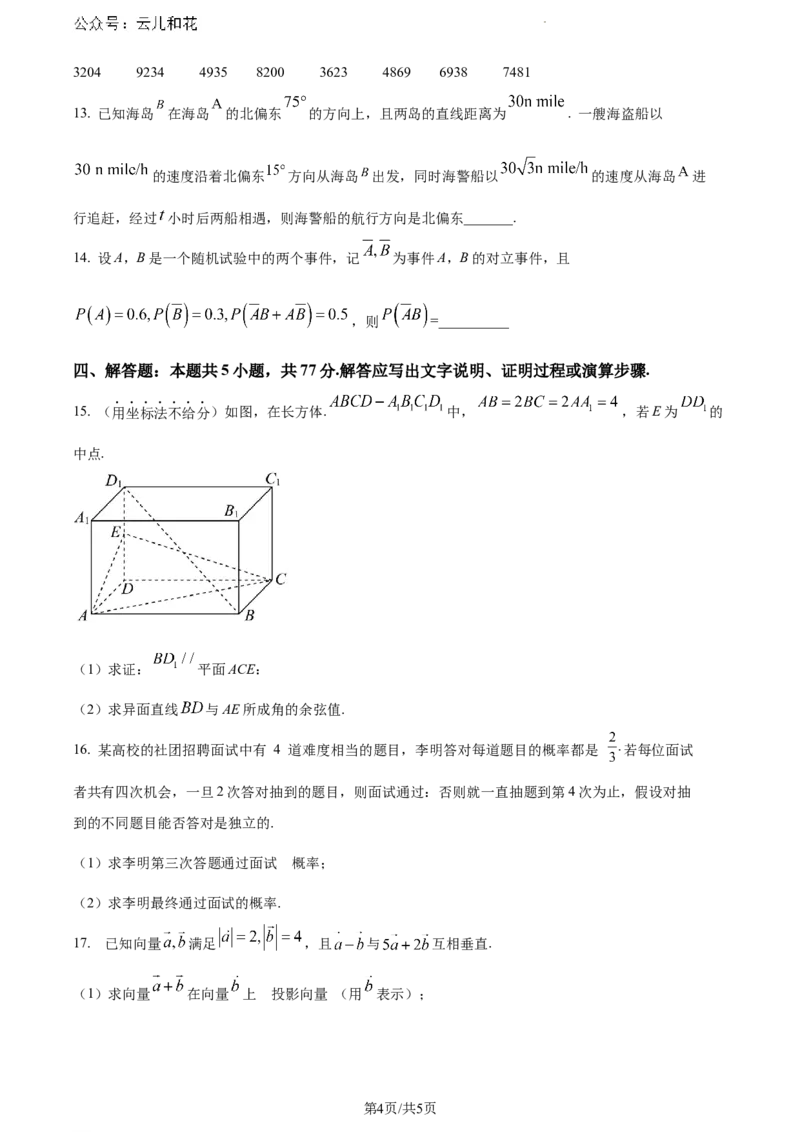
15. (用坐标法不给分)如图,在长方体. 中, ,若E为 的
中点.
(1)求证: 平面ACE:
(2)求异面直线 与AE所成角的余弦值.
16. 某高校的社团招聘面试中有 4 道难度相当的题目,李明答对每道题目的概率都是 若每位面试
者共有四次机会,一旦2次答对抽到的题目,则面试通过:否则就一直抽题到第4次为止,假设对抽
到的不同题目能否答对是独立的.
的
(1)求李明第三次答题通过面试 概率;
(2)求李明最终通过面试的概率.
17. 已知向量 满足 ,且 与 互相垂直.
的
(1)求向量 在向量 上 投影向量 (用 表示);
第4页/共5页
学科网(北京)股份有限公司(2)定义平面非零向量之间的一种运算“*”: (其中 是非零向量 和 的夹角),
求
18. 在 中,内角 , , 所对的边分别为 , , ,
(1)已知 ,
(i)求 ;
(ii)若 , 为 边上的中点,求 的长.
(2)若 为锐角三角形,求证:
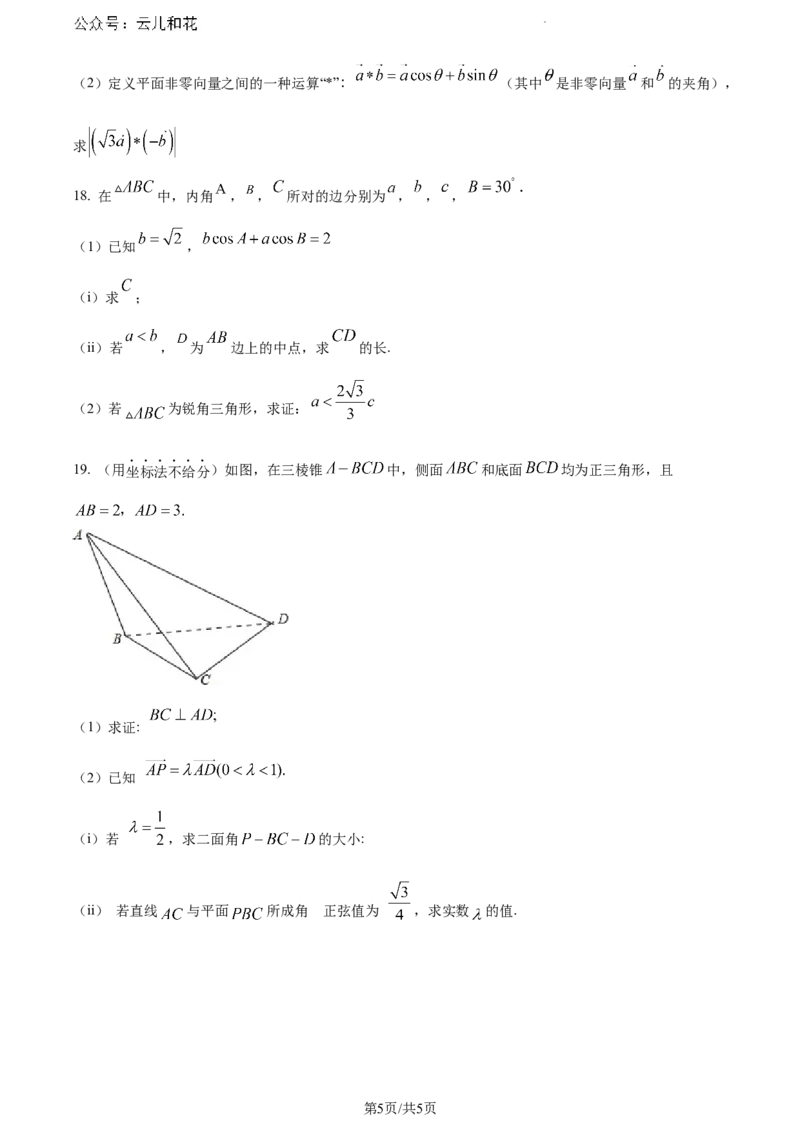
19. (用坐标法不给分)如图,在三棱锥 中,侧面 和底面 均为正三角形,且
(1)求证:
(2)已知
(i)若 ,求二面角 的大小:
(ii) 若直线 与平面 所成角 的正弦值为 ,求实数 的值.
第5页/共5页
学科网(北京)股份有限公司