文档内容
2024 学年第二学期衢州五校联盟期中联考
高一年级数学学科试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合题目要求的
1. 设集合 ,则 ( )
A. B. C. D.
2. “ ”是“ ”成立的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分条件 D. 既不充分也不必要条件
3. 已知函数 的定义域为 ,则实数 的取值范围( )
.
A 或 B. C. D.
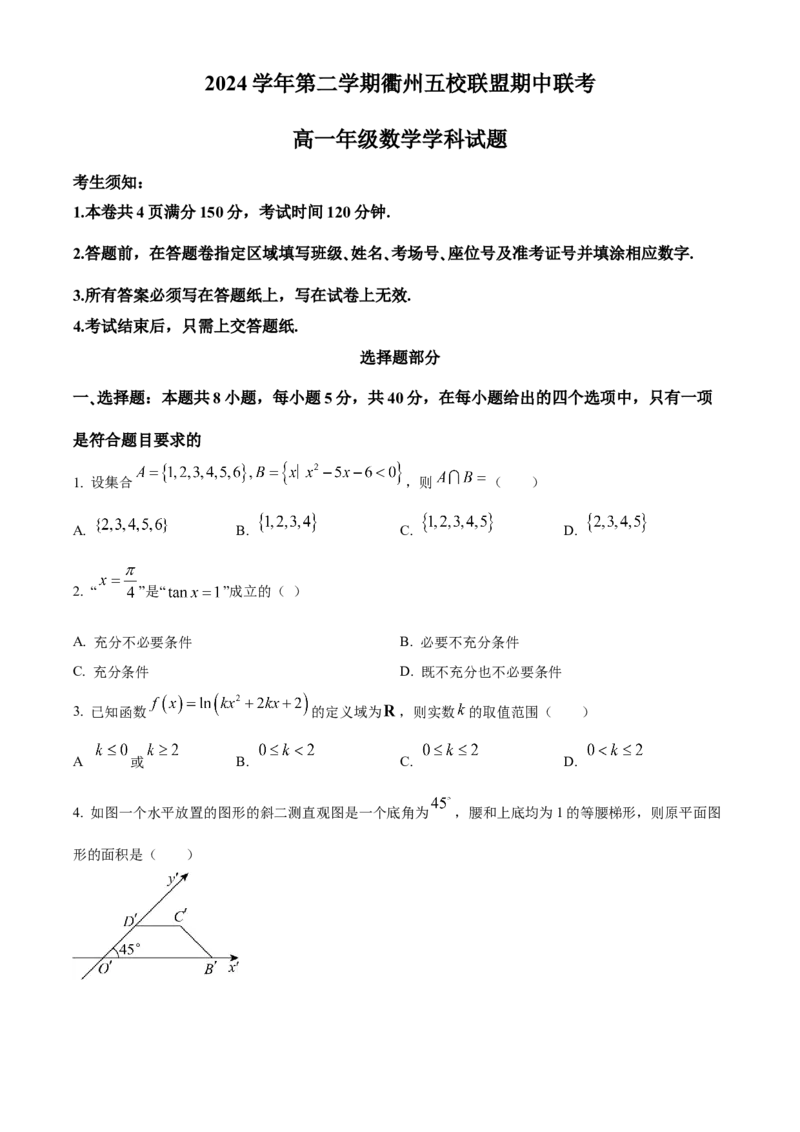
4. 如图一个水平放置的图形的斜二测直观图是一个底角为 ,腰和上底均为1的等腰梯形,则原平面图
形的面积是( )A. B. C. D.
5. 关于函数 ,下列说法不正确的是( )
A. 周期为 B. 在 上不单调
C. 是它的一条对称轴 D. 有一个对称中心
6. 若 ,且 在 方向上的投影向量为 ,则 与 的夹角为( )
.
A B. C. D.
7. 灵山江畔的龙洲塔,有“人文荟萃,学养深厚”的福地一说.如图,某同学为了测量龙洲塔的高度,在地面
处测得塔在南偏东 的方向上,向正南方向行走 后到达D处,测得塔在南偏东 的方向上,
处测得塔尖 的仰角为 ,则可得龙洲塔高度为( )
A. B. C. D.
8. 定义在 上的偶函数 满足:当 时, ,且当 时,,则 的零点个数是( )
A. 6个 B. 7个 C. 8个 D. 无数个
二、多选题:本题共3小题,每小题6分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错或不选的得0分.
9. 下列各组函数的图象,能够通过左右平移实现重合的是( )
A. 与 B. 与
C. 与 D. 与
10. 在 中,内角 所对的边分别是 ,则下列说法正确的是( )
A. 若 ,则 的外接圆的面积是
B. 若 ,则 是等腰三角形
C. 若 ,则 可能等于10
D. 若 ,则 面积为 或
的
11. 在 中, 是 中点, 与BD交于点F,则下列说法正确的是(
)
A. B.
.
C D.
非选择题部分
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知复数 是方程 的一个根,则复数 的模 的值为__________.
13. 古希腊几何学家海伦和我国宋代数学家秦九䇉都曾提出利用三角形的三边求面积的公式,称为海伦—秦九韶公式:如果一个三角形的三边长分别是 ,记 ,则三角形面积为
.已知 中, ,则 的内切圆半径 为
__________.
14. 在正四面体ABCD中, 分别为 的中点, ,截面EFG将四面体分成两部分,
则体积较大部分与体积较小部分的体积之比是__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
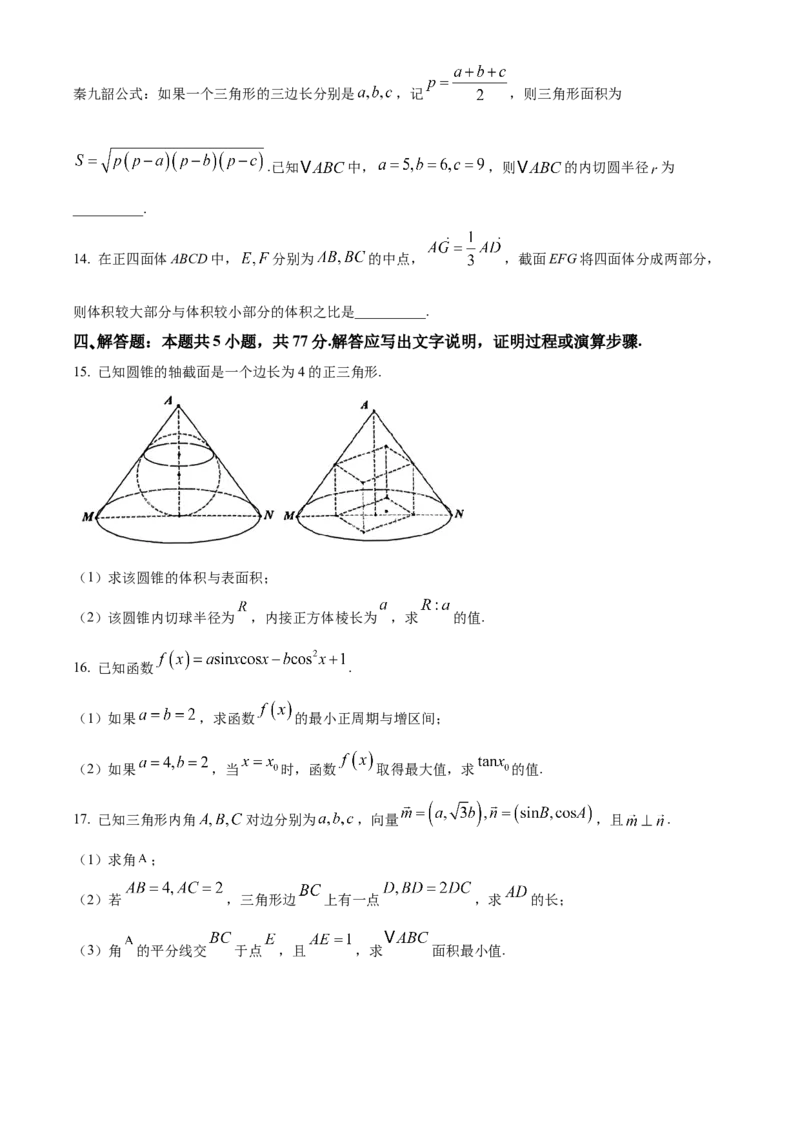
15. 已知圆锥的轴截面是一个边长为4的正三角形.
(1)求该圆锥的体积与表面积;
(2)该圆锥内切球半径为 ,内接正方体棱长为 ,求 的值.
16. 已知函数 .
(1)如果 ,求函数 的最小正周期与增区间;
(2)如果 ,当 时,函数 取得最大值,求 的值.
17. 已知三角形内角 对边分别为 ,向量 ,且 .
(1)求角 ;
(2)若 ,三角形边 上有一点 ,求 的长;
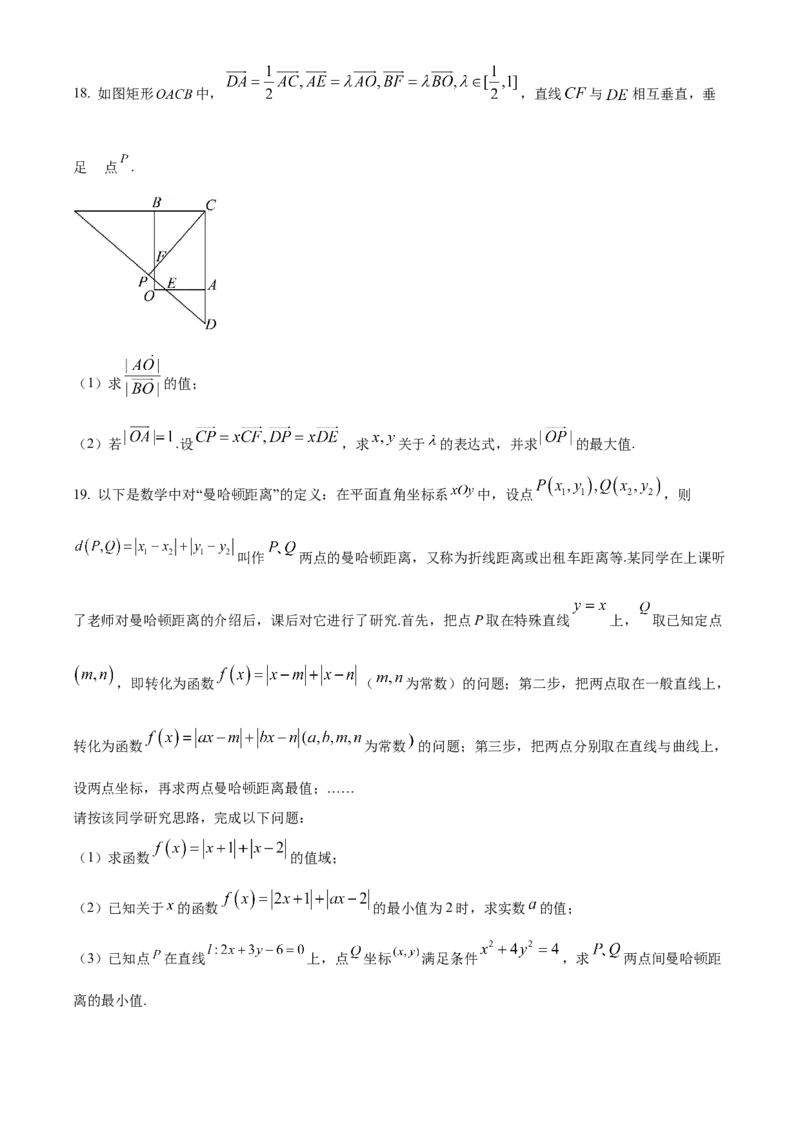
(3)角 的平分线交 于点 ,且 ,求 面积最小值.18. 如图矩形 中, ,直线 与 相互垂直,垂
为
足 点 .
(1)求 的值;
(2)若 .设 ,求 关于 的表达式,并求 的最大值.
19. 以下是数学中对“曼哈顿距离”的定义:在平面直角坐标系 中,设点 ,则
叫作 两点的曼哈顿距离,又称为折线距离或出租车距离等.某同学在上课听
了老师对曼哈顿距离的介绍后,课后对它进行了研究.首先,把点P取在特殊直线 上, 取已知定点
,即转化为函数 ( 为常数)的问题;第二步,把两点取在一般直线上,
转化为函数 为常数 的问题;第三步,把两点分别取在直线与曲线上,
设两点坐标,再求两点曼哈顿距离最值;……
请按该同学研究思路,完成以下问题:
(1)求函数 的值域;
(2)已知关于 的函数 的最小值为2时,求实数 的值;
(3)已知点 在直线 上,点 坐标 满足条件 ,求 两点间曼哈顿距
离的最小值.2024 学年第二学期衢州五校联盟期中联考
高一年级数学学科试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合题目要求的
【1题答案】
【答案】C
【2题答案】
【答案】A
【3题答案】
【答案】B
【4题答案】
【答案】A
【5题答案】
【答案】D
【6题答案】
【答案】B
【7题答案】
【答案】C
【8题答案】
【答案】C
二、多选题:本题共3小题,每小题6分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错或不选的得0分.
【9题答案】【答案】AD
【10题答案】
【答案】ACD
【11题答案】
【答案】BCD
非选择题部分
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
【15题答案】
【答案】(1) ,
(2)
【16题答案】
【答案】(1) ,增区间为
(2)
【17题答案】
【答案】(1)(2)
(3)
【18题答案】
【答案】(1)
(2) , 的最大值为 .
【19题答案】
【答案】(1)
(2) 或0
(3)