文档内容
黄金冲刺大题05 导数(精选30题)
1.(2024·安徽·二模)已知函数 .
(1)求函数 在点 处的切线方程;
(2)求 的单调区间和极值.
【答案】(1) ;
(2)递增区间为 ,递减区间为 ,极大值 ,极小值 .
【分析】(1)求出函数 的导数,赋值求得 ,再利用导数的几何意义求出切线方程.
(2)由(1)的信息,求出函数 的导数,利用导数求出单调区间及极值.
【详解】(1)函数 ,求导得 ,
则 ,解得 ,于是 , ,
所以所求切线方程为: ,即 .
(2)由(1)知,函数 ,定义域为 ,
求导得 ,
当 或 时, ,当 时, ,
因此函数 在 上单调递增,在 上单调递减,
当 时, 取得极大值 ,
当 时, 取得极小值 ,
所以函数 的递增区间为 ,递减区间为 ,
极大值 ,极小值 .
2.(2024·江苏南京·二模)已知函数 ,其中 .(1)当 时,求曲线 在 处的切线方程;
(2)当 时,若 在区间 上的最小值为 ,求a的值.
【答案】(1)
(2)
【分析】(1)由 ,分别求出 及 ,即可写出切线方程;
(2)计算出 ,令 ,解得 或 ,分类讨论 的范围,得出 的单调性,由 在区
间 上的最小值为 ,列出方程求解即可.
【详解】(1)当 时, ,则 , ,所以 ,
所以曲线 在 处的切线方程为: ,即 .
(2) ,令 ,解得 或 ,
当 时, 时, ,则 在 上单调递减,
所以 ,则 ,符合题意;
当 时, 时, ,则 在 上单调递减,
时, ,则 在 上单调递增,
所以 ,则 ,不合题意;
当 时, 时, ,则 在 上单调递减,
所以 ,不合题意;
综上, .3.(2024·浙江绍兴·模拟预测)已知 , .
(1)讨论 的单调性.
(2)若 使得 ,求参数 的取值范围.
【答案】(1)当 时, 在 上单调递减;当 时, 在 上单调递减,在
上单调递增.
(2)
【分析】(1)对 求导数,然后分类讨论即可;
(2)直接对 和 分类讨论,即可得到结果.
【详解】(1)由 ,知 .
当 时,有 ,所以 在 上单调递减;
当 时,对 有 ,
对 有 ,
所以 在 上单调递减,在 上单调递增.
综上,当 时, 在 上单调递减;
当 时, 在 上单调递减,在 上单调递增.
(2)当 时,由(1)的结论,知 在 上单调递减,在 上单调递增,
所以对任意的 都有 ,
故 恒成立,这表明此时条件不满足;当 时,设 ,由于
,
,
故由零点存在定理,知一定存在 ,使得 ,
故 ,从而 ,这表明此时条件满足.
综上, 的取值范围是 .
4.(2024·福建漳州·一模)已知函数 , 且 .
(1)证明:曲线 在点 处的切线方程过坐标原点.
(2)讨论函数 的单调性.
【答案】(1)证明见解析
(2)答案见解析
【分析】(1)先利用导数的几何意义求得 在 处的切线方程,从而得证;
(2)分类讨论 与 ,利用导数与函数的单调性即可得解.
【详解】(1)因为 ,所以 ,
则 , ,
所以 在 处的切线方程为: ,
当 时, ,故 ,
所以曲线 在点 处切线的方程过坐标原点.
(2)由(1)得 ,当 时, ,则 ,故 单调递减;
当 时,令 则 ,
当 时, , 单调递增;
当 时, , 单调递减;
综上:当 时, 在 上单调递减;
当 时, 在 上单调递增,在 上单调递减.
5.(2024·山东·二模)已知函数 .
(1)当 时,求 的单调区间;
(2)当 时, ,求 的取值范围.
【答案】(1) 的减区间为 ,增区间为
(2)
【分析】(1)当 时, ,求导得 ,令 ,
求 确定 的单调性与取值,从而确定 的零点,得函数的单调区间;
(2)求 ,确定函数的单调性,从而确定函数 的最值,即可得 的取值范围.
【详解】(1)当 时, ,
则 ,
设 ,则 恒成立,又 ,
所以当 时, , 单调递减,当 时, , 单调递增,
所以 的减区间为 ,增区间为 ;(2) ,
设 ,则 ,所以 在 上单调递增,
又 , ,
所以存在 ,使得 ,即 ,
当 时, , 单调递减,
当 时, , 单调递增,
当 时, 取得极小值,也是最小值,
所以 ,
所以 ,即 ,
设 ,易知 单调递增,且 ,
所以 ,解得 ,
综上, .
6.(2024·山东·一模)已知函数 .
(1)当 时,求函数 的单调区间;
(2)若函数 有两个极值点 ,且 ,求a的取值范围.
【答案】(1)增区间 ,减区间
(2)
【分析】(1)将 代入求导,然后确定单调性即可;(2)求导,根据导函数有两个根写出韦达定理,代入 ,构造函数,求导,研究函数
性质进而求出a的取值范围.
【详解】(1)当 时, , ,
则 ,
当 , , 单调递增,当 , , 单调递减,
所以 的单调递增区间是 ,单调递减区间是 ;
(2) ,
所以 ,
设 ,令 ,由于 有两个极值点 ,
所以 ,解得 .
由 , ,
得
,
即 ,令 ,
则 ,
所以 在 上单调递减,且 ,所以 ,故a的取值范围是 .
7.(2024·湖北·二模)求解下列问题,
(1)若 恒成立,求实数k的最小值;
(2)已知a,b为正实数, ,求函数 的极值.
【答案】(1)1
(2)答案见解析
【分析】(1)求导,然后分 和 讨论,确定单调性,进而得最值;
(2)先发现 ,当 时, ,当 , 时,取 , ,
求导,研究单调性,进而求出最值得答案.
【详解】(1)记 ,则需使 恒成立,
,
当 时, 恒成立,则 在 上单调递减,
且在 时, ,不符合题意,舍去;
当 时.令 ,解得 ,
则 在 上单调递减,在 上单调递增,
所以 ,
要使 恒成立,只要 即可,
解得 ,所以k的最小值为1;
(2) , , , ,易知 ,
当 时, ,此时函数无极值;当 , 时, ,
取 , , , , , , ,
则 ,当 时,由 得 ,由(1)知 ,
当 时, ,
因为 ,所以 ,所以 ,即 ,当 时, ,
所以 ,则 ,所以 ,
即 在 上单调递增,在 单调递减.
所以函数 , , ,
当 时,同理有 ,
由 得 ,即 在 上单调递增,在 上单调递减.
所以函数 , , ,
综上可知,当 时,函数 没有极值;当 时,函数 有唯一的极大值 ,其中,没有极小值.
【点睛】关键点点睛:取 ,将两个参数的问题转化为一个参数的问题,进而求导解答问题.
8.(2024·湖北武汉·模拟预测)函数
.
(1)求函数 的极值;
(2)若 恒成立,求 的最大值.
【答案】(1)极小值为 ,极大值为 ;
(2)3.
【分析】(1)判断函数 为奇函数,利用导数求出 在区间 上的极值,利用奇偶性即可求得定
义域上的极值.
(2)利用导数证明当 时, 恒成立,当 时,等价变形不等式并构造函数
,利用导数并按导数为负为正确定 的取值范围,进而确定不等式恒成立与否
得解.
【详解】(1)函数 , ,
即函数 为奇函数,其图象关于原点对称,
当 时, ,求导得:
,
由于 ,由 ,得 ,解得 ,由 ,得 ,解得 ,即 在 上单调递减,在 上单调递增,
因此函数 在 上有极小值 ,
从而 在 上的极小值为 ,极大值为 .
(2)当 时, 恒成立,即 恒成立,亦即 恒成立,
令 ,求导得 ,
则函数 在 上为增函数,有 ,因此 恒成立;
当 时, 恒成立,即不等式 恒成立,
令 ,求导得:
令 ,求导得则
,
由 ,得 ,
当 时,即 时, ,则函数 在 上单调递减,则有 ,即 ,因此函数 在 上单调递减,有 ,即 ,
当 时,即 时,存在一个 ,使得 ,
且当 时, ,即 在 上单调递增,且 ,
则 ,于是 在 上单调递增,因此 ,即 ,与 矛盾,
所以 的最大值为3.
【点睛】方法点睛:对于利用导数研究不等式的恒成立与有解问题的求解策略:
①通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;
②利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.
③根据恒成立或有解求解参数的取值时,一般涉及分离参数法,但压轴试题中很少碰到分离参数后构造的
新函数能直接求出最值点的情况,进行求解,若参变分离不易求解问题,就要考虑利用分类讨论法和放缩
法,注意恒成立与存在性问题的区别.
9.(2024·湖北·模拟预测)已知函数 , ,
(1)若对定义域内任意非零实数 , ,均有 ,求a;
(2)记 ,证明: .
【答案】(1)
(2)证明见解析
【分析】(1)求导可得 ,再分 与 两种情况分析原函数的单调性,当 时分析极值
点的正负与原函数的正负区间,从而确定 的值;
(2)由(1)问的结论可知, ,再累加结合放缩方法证明即可.
【详解】(1) 的定义域为 ,且 ;,因此 ;
i. 时, ,则此时令 有 ,令 有 ,
则 在 上单调递增, 上单调递减,又 ,
于是 ,此时令 ,有 ,不符合题意;
ii. 时, 有零点0和 ,
若 ,即 ,此时令 有 , 在 上单调递减,
又 ,则 ,令 , ,有 ,不符合题意;
若 ,即 ,此时令 有 , 在 上单调递减,
又 ,则 ,令 ,有 ,不符合题意;
若 ,即 ,此时 , 在 上单调递增,又 ,
则 时 , 时 ;则 时 ,也即对 , ,
综上,
(2)证:由(1)问的结论可知, 时, ;
且 时 , ;
则 时, ,令 ,有 ,
即 ,于是
将上述n个式子相加, ;
欲证 ,只需证 ,只需证 ;
因为 ,
所以 ,得证:
于是得证 .
【点睛】方法点睛:
(1)此题考导数与函数的综合应用,找到合适的分类标准,设极值点,并确定函数正负区间是解此题的
关键;
(2)对累加结构的不等式证明,一般需要应用前问的结论,取特定参数值,得出不等式累加证明,遇到
不能累加的数列结构,需要进行放缩证明.
10.(2024·湖南·一模)已知函数 .
(1)当 时,求函数 在 处的切线方程;
(2) 时;
(ⅰ)若 ,求 的取值范围;
(ⅱ)证明: .【答案】(1)
(2)
(ⅰ) (ⅱ)证明见解析
【分析】(1)令 时,利用导数的几何意义求出斜率,进行计算求出切线方程即可.
(2)(ⅰ)设 由 得 ,再证明此时满足 .
(ⅱ)根据(ⅰ)结论判断出 在 上单调递增, 即
【详解】(1)当 时,
所以切线方程为: 即
(2)(ⅰ)
即 ,
设
又 是 的一个必要条件,即
下证 时,满足
又 ,
设 在 上单调递减,
所以 ,
又 即 在 单调递增.时, ;
下面证明 时不满足 ,
,
令 ,
则 ,
,
∴ 在 为增函数,
令 满足 ,
则 ,
又 ∴ ,使得 ,
当 时, ,
∴此时 在 为减函数,
当 时, ,
∴ 时,不满足 恒成立.
综上 .
(ⅱ)设由(ⅰ)知 ,
在 上单调递增, 即
【点睛】关键点点睛:本题考查导数,解题关键是进行必要性探路,然后证明充分性,得到所要求的参数
范围即可.
11.(2024·全国·模拟预测)已知函数 .
(1)求曲线 在 处的切线方程;
(2)若 ,讨论曲线 与曲线 的交点个数.
【答案】(1) ;
(2)2.
【分析】(1)求导,即可根据点斜式求解方程,
(2)求导,分类讨论求解函数的单调性,结合零点存在性定理,即可根据函数的单调性,结合最值求解.
【详解】(1)依题意, ,故 ,
而 ,故所求切线方程为 ,即 .
(2)令 ,故 ,
令 ,
,令 ,
.①当 时, ,
在 上为减函数,即 在 上为减函数,
又 ,
在 上有唯一的零点,设为 ,即 .
在 上为增函数,在 上为减函数.
又
,
在 上有且只有一个零点,在 上无零点;
②当 时, 单调递减,
又 ,
在 内恰有一零点;
③当 时, 为增函数,
,
单调递增,又 ,所以存在唯一 ,当 时, 递减;当 时, 递增,
,
在 内无零点.综上所述,曲线 与曲线 的交点个数为2.
【点睛】方法点睛:本题考查了导数的综合运用,求某点处的切线方程较为简单,利用导数求单调性时,
如果求导后的正负不容易辨别,往往可以将导函数的一部分抽离出来,构造新的函数,利用导数研究其单
调性,进而可判断原函数的单调性.在证明不等式时,常采用两种思路:求直接求最值和等价转化.无论是
那种方式,都要敢于构造函数,构造有效的函数往往是解题的关键.
12.(2024·广东佛山·二模)已知 .
(1)当 时,求 的单调区间;
(2)若 有两个极值点 , ,证明: .
【答案】(1)答案见解析
(2)证明见解析
【分析】(1)求导后,借助导数的正负即可得原函数的单调性;
(2)借助换元法,令 , , ,可得 、 是方程 的两个正根,借助韦达定理
可得 , ,即可用 、 表示 ,进而用 表示 ,
构造相关函数后借助导数研究其最大值即可得.
【详解】(1)当 时, ,
,
则当 ,即 时, ,当 ,即 时, ,
故 的单调递减区间为 、 ,单调递增区间为 ;
(2) ,令 ,即 ,
令 , ,则 、 是方程 的两个正根,
则 ,即 ,
有 , ,即 ,
则
,
要证 ,即证 ,
令 ,
则 ,
令 ,则 ,
则 在 上单调递减,
又 , ,
故存在 ,使 ,即 ,则当 时, ,当 时, ,
故 在 上单调递增, 在 上单调递减,
则 ,
又 ,则 ,故 ,
即 ,即 .
【点睛】关键点点睛:本题关键点在于借助换元法,令 , , ,从而可结合韦达定理得 、
的关系,即可用 表示 ,构造相关函数后借助导数研究其最大值即可得.
13.(2024·广东广州·模拟预测)已知函数 .
(1)当 时,求函数 的极值;
(2)若函数 在 上仅有两个零点,求实数 的取值范围.
【答案】(1)极小值为 ,无极大值
(2)
【分析】(1)求出导函数,然后列表求出函数的单调区间,根据极值定义即可求解;
(2)把原函数有两个零点转化为 在 上仅有两个零点,分类讨论,利用导数研究函数
的单调性,列不等式求解即可.
【详解】(1)当 时, R),所以 ,
令 ,则 ,- 0 +
单调递
极小值 单调递增
减
所以 ,
所以 的极小值为 ,无极大值.
(2)函数 在 上仅有两个零点,
令 ,则问题等价于 在 上仅有两个零点,
易知 ,因为 ,所以 .
①当 时, 在 上恒成立,所以 在 上单调递增,
所以 ,所以 在 上没有零点,不符合题意;
②当 时,令 ,得 ,
所以在 上, ,在 上, ,
所以 在 上单调递减,在 上单调递增,
所以 的最小值为 .
因为 在 上有两个零点,所以 ,所以 .
因为 ,
令 ,则 ,
所以在 上, ,在 上, ,
所以 在 上单调递减,在 上单调递增,所以 ,所以 ,
所以当 时, 在 和 内各有一个零点,
即当 时, 在 上仅有两个零点.
综上,实数 的取值范围是 .
【点睛】方法点睛:求解函数单调区间的步骤:
(1)确定 的定义域.
(2)计算导数 .
(3)求出 的根.
(4)用 的根将 的定义域分成若干个区间,判断这若干个区间内 的符号,进而确定
的单调区间. ,则 在对应区间上单调递增,对应区间为增区间; ,则 在
对应区间上单调递减,对应区间为减区间.
如果导函数含有参数,那么需要对参数进行分类讨论,分类讨论要做到不重不漏.
14.(2024·江苏南通·二模)已知函数 , , .
(1)求函数 的单调区间;
(2)若 且 恒成立,求 的最小值.
【答案】(1)答案见解析
(2) .
【分析】(1)求导后,利用导数与函数单调性的关系,对 与 分类讨论即可得;
(2)结合函数的单调性求出函数的最值,即可得解.
【详解】(1) ( ),当 时,由于 ,所以 恒成立,从而 在 上递增;
当 时, , ; , ,
从而 在 上递增,在 递减;
综上,当 时, 的单调递增区间为 ,没有单调递减区间;
当 时, 的单调递增区间为 ,单调递减区间为 .
(2)令 ,要使 恒成立,
只要使 恒成立,也只要使 .
,
由于 , ,所以 恒成立,
当 时, ,当 时, ,
所以 ,解得: ,
所以 的最小值为 .
15.(2024·山东济南·二模)已知函数
(1)讨论 的单调性;
(2)证明: .
【答案】(1)答案见详解
(2)证明见详解
【分析】(1)求导可得 ,分 和 两种情况,结合导函数的符号判断原函数单调性;(2)构建 , ,根据单调性以及零点存在性定理分析 的
零点和符号,进而可得 的单调性和最值,结合零点代换分析证明.
【详解】(1)由题意可得: 的定义域为 , ,
当 时,则 在 上恒成立,
可知 在 上单调递减;
当 时,令 ,解得 ;令 ,解得 ;
可知 在 上单调递减,在 上单调递增;
综上所述:当 时, 在 上单调递减;
当 时, 在 上单调递减,在 上单调递增.
(2)构建 ,
则 ,
由 可知 ,
构建 ,
因为 在 上单调递增,则 在 上单调递增,
且 ,
可知 在 上存在唯一零点 ,当 ,则 ,即 ;
当 ,则 ,即 ;
可知 在 上单调递减,在 上单调递增,
则 ,
又因为 ,则 , ,
可得 ,
即 ,所以 .
16.(2024·福建·模拟预测)已知函数 在 处的切线在 轴上的截距为 .
(1)求 的值;
(2)若 有且仅有两个零点,求 的取值范围.
【答案】(1)2
(2)
【分析】(1)借助导数的几何意义计算即可得;
(2)借助函数与方程的关系,可将 有且仅有两个零点转化为方程 有两个根,构造对应函数
并借助导数研究单调性及值域即可得.
【详解】(1) , , ,
则函数 在 处的切线为: ,
即 ,令 ,则有 ,即 ;
(2)由 ,即 ,若 有且仅有两个零点,则方程 有两个根,
即方程 有两个根,
令 ,则 ,
则当 时, ,则当 时, ,
故 在 上单调递增,在 上单调递减,
故 ,
又 时, , 时, ,
故当 时,方程 有两个根,即 有且仅有两个零点.
17.(2024·浙江杭州·二模)已知函数 .
(1)讨论函数 的单调性;
(2)若函数 有两个极值点,
(ⅰ)求实数 的取值范围;
(ⅱ)证明:函数 有且只有一个零点.
【答案】(1)答案见解析;
(2)(ⅰ) ;(ⅱ)证明见解析
【分析】(1)求出函数的导函数,再分 、 、 三种情况,分别求出函数的单调区间;
(2)(ⅰ)由(1)直接解得;(ⅱ)结合函数的最值与零点存在性定理证明即可.
【详解】(1)函数 的定义域为 ,
且 ,当 时, 恒成立,所以 在 单调递减;
当 时,令 ,即 ,解得 , ,
因为 ,所以 ,则 ,
所以当 时 ,
当 时 ,
当 时 ,
所以 在 上单调递减,在 上单调递增,
在 上单调递减;
当 时,此时 ,
所以 时 ,当 时 ,
所以 在 上单调递增,在 上单调递减.
综上可得:当 时 在 单调递减;
当 时 在 上单调递减,
在 上单调递增,在 上单调递减;
当 时 在 上单调递增,在 上单调递减.
(2)(ⅰ)由(1)可知 .
(ⅱ)由(1) 在 上单调递减,
在 上单调递增,在 上单调递减,
所以 在 处取得极大值,在 处取得极小值,又 ,所以 ,则 ,
又 ,
又 ,
所以 在 上没有零点,
又 ,则 ,则 , ,
则 ,
所以 ,所以 在 上存在一个零点,
综上可得函数 有且只有一个零点.
18.(2024·河北沧州·模拟预测)已知函数 , .
(1)讨论 的单调性;
(2)若 , 恒成立,求实数a的取值范围.
【答案】(1)答案见解析
(2) .
【分析】(1)利用导数分类讨论判断函数 的单调性,即可求解;
(2)先利用导数证明不等式 ,分离变量可得 恒成立,进而
,即可求解.
【详解】(1)函数 , 的定义域为 ,且 .当 时, , 恒成立,此时 在区间 上单调递增;
当 时,令 ,解得 ,
当 时, , 在区间 上单调递增,
当 时, , 在区间 上单调递减.
综上所述,当 时, 在区间 上单调递增;
当 时, 在区间 上单调递增,在区间 上单调递减.
(2)设 ,则 ,
在区间 上, , 单调递减,在区间 上, , 单调递增,
所以 ,所以 (当且仅当 时等号成立).
依题意, , 恒成立,即 恒成立,
而 ,
当且仅当 时等号成立.
因为函数 在 上单调递增, , ,
所以存在 ,使得 成立.
所以 ,即a的取值范围是 .
【点睛】方法点睛:利用导数证明不等式的恒成立问题的求解策略:
形如 的恒成立的求解策略:
1、构造函数法:令 ,利用导数求得函数 的单调性与最小值,只需 恒成立即可;
2、参数分离法:转化为 或 恒成立,即 或 恒成立,只需利用导数求
得函数 的单调性与最值即可;
3,数形结合法:结合函数 的图象在 的图象的上方(或下方),进而得到不等式恒成立.
19.(2024·广东·二模)已知 .
(1)求 的单调区间;
(2)函数 的图象上是否存在两点 (其中 ),使得直线 与函数 的图象
在 处的切线平行?若存在,请求出直线 ;若不存在,请说明理由.
【答案】(1) 在 上单调递减,在 上单调递增.
(2)不存在,理由见解析
【分析】(1)求出导函数,根据导函数的正负来确定函数的单调区间;
(2)求出直线 的斜率,再求出 ,从而得到 的等式,再进行换元和求导,即可解出答案.
【详解】(1)由题可得
因为 ,所以 ,
所以当 时, , 在 上单调递减,
当 时, , 在 上单调递增.
综上, 在 上单调递减,在 上单调递增.
(2)由题意得,斜率,
,
由 得,
,即 ,即
令 ,不妨设 ,则 ,
记
所以 ,所以 在 上是增函数,所以 ,
所以方程 无解,则满足条件的两点 不存在.
20.(2024·广东深圳·二模)已知函数 , 是 的导函数,且 .
(1)若曲线 在 处的切线为 ,求k,b的值;
(2)在(1)的条件下,证明: .
【答案】(1) , ;
(2)证明见解析.
【分析】(1)根据题意,求导可得 的值,再由导数意义可求切线,得到答案;
(2)设函数 ,利用导数研究函数 的单调性从而求出最小值大于0,可得证.
【详解】(1)因为 ,所以 ,
因为 ,所以 .则曲线 在点 处的切线斜率为 .
又因为 ,
所以曲线 在点 处的切线方程为 ,
即得 , .
(2)设函数 , ,
则 ,
设 ,则 ,
所以,当 时, , 单调递增.
又因为 ,
所以, 时, , 单调递增;
时, , 单调递减.
又当 时, ,
综上 在 上单调递减,在 上单调递增,
所以当 时, 取得最小值 ,
即 ,
所以,当 时, .
21.(2024·辽宁·二模)已知函数 .
(1)若曲线 在 处的切线方程为 ,求实数 的值;
(2)若对于任意 , 恒成立,求实数 的取值范围.【答案】(1) ,
(2)
【分析】(1)根据导数几何意义和切线方程,可直接构造方程组求得结果;
(2)构造函数 ,将问题转化为 恒成立;求导后,分别在 、
和 的情况下,结合单调性和最值求得符合题意的范围.
【详解】(1) , ,
在 处的切线为 , ,
解得: , .
(2)由 得: ,
令 ,则当 时, 恒成立;
;
①当 时, , , ,
在 上单调递减, ,不合题意;
②当 时, ,
i.当 ,即 时, 在 上恒成立,
在 上单调递增, ,符合题意;ii.当 ,即 时,
若 ,则 , 在 上单调递减,
此时 ,不合题意;
综上所述:实数 的取值范围为 .
22.(2024·黑龙江哈尔滨·一模)已知函数 .
(1)当 时,求 在 处的切线方程;
(2)当 时,求 的单调区间和极值;
(3)若对任意 ,有 恒成立,求 的取值范围.
【答案】(1)
(2) 的单调递减区间为: ;递增区间为: ,
的极大值为 ,无极小值
(3)
【分析】(1)利用已知确定切点,导数的几何意义确定斜率,求出切线方程即可.
(2)利用导数先求解单调性,再确定极值即可.
(3)利用分离参数法结合导数求解参数范围即可.
【详解】(1)当 时, ,
则 , , ,
所以切线方程为 .(2)当 时, , .
令 , ,
故 在R上单调递减,而 ,因此0是 在R上的唯一零点
即:0是 在R上的唯一零点
当x变化时, , 的变化情况如下表:
x 0
0
极大值
的单调递减区间为: ;递增区间为:
的极大值为 ,无极小值
(3)由题意知 ,即 ,即 ,
设 ,则 ,
令 ,解得 ,
当 , , 单调递增,
当 , , 单调递减,
所以 ,
所以23.(2024·安徽合肥·二模)已知曲线 在点 处的切线为 .
(1)求直线 的方程;
(2)证明:除点 外,曲线 在直线 的下方;
(3)设 ,求证: .
【答案】(1) ;
(2)证明见解析;
(3)证明见解析.
【分析】(1)求导,得到 ,利用导数的几何意义写出切线方程;
(2)令 ,二次求导得到函数单调性,结合特殊点函数值,得到所以 ,
当且仅当 等号成立,得到证明;
(3)求导得到 的单调性,结合函数图象得到 ,不妨令 ,结合曲线 在 点
的切线方程为 ,得到 ,转化为证明 ,又 ,只要证
,令 ,求导得到函数单调性,结合特殊点函数值得到答案.
【详解】(1)因为 ,
所以 ,
所以直线 的方程为: ,即
(2)令 ,则 ,
令 ,则 ,
由 ,解得 ,由 ,解得 ,
所以 在 上单调递减,在 上单调递增,当 时, ,
所以 在 上单调递减,在 上单调递增,
所以 ,当且仅当 等号成立,
所以除切点 之外,曲线 在直线 的下方.
(3)由 ,解得 ,解得 ,
所以 在 上单调递增,在 上单调递减,
,
当 时, .
因为 ,则 ,不妨令 .
因为曲线 在 点的切线方程为 ,
设点 在切线上,有 ,故 ,
由(1)知 时, ,
则 ,即 ,
要证: ,
只要证: ,只要证: ,
又 ,
只要证: ,
令 ,
则 ,
易证 在 上单调递增,在 上单调递减,
所以 ,
所以 在 上单调递减,所以 成立,
所以原命题成立.
【点睛】关键点点睛:本题关键是利用函数在零点处的切线方程,得到 ,且 ,
从而只需证明 ,再勾股函数进行求解.
24.(2024·江苏扬州·模拟预测)已知函数 .
(1)讨论函数 的单调性;
(2)若存在正数 ,使 成立,求 的取值范围;
(3)若 ,证明:对任意 ,存在唯一的实数 ,使得 成立.
【答案】(1)当 时, 在 上单调递增;当 时, 在 上单调递增,在
上单调递减.(2)
(3)证明见解析
【分析】(1)计算 ,然后分类讨论即可得到单调性;
(2)对 和 两种情况分别讨论,即可得到取值范围是 ;
(3)首先证明 单调递减,即得唯一性;然后求导证明对任意的 ,都有 ;而对任意的
,都有 . 再利用该结论证明 ,从而得到存在性. 最后综合两方面
即证得结论.
【详解】(1)对 求导得 .
当 时,对 有 ,故 在 上单调递增;
当 时,有 ,而当 时,
,故当 时 ,当 时 ,从而 在 上单调递
增,在 上单调递减.
综上,当 时, 在 上单调递增;
当 时, 在 上单调递增,在 上单调递减.(2)若 ,由于 ,故存在正数 使得 ,条件满足;
若 ,则由(1)的结论,知 在 上单调递增,在 上单调递减,从而此时对任意的
都有 ,条件不满足.
综上, 的取值范围是 .
(3)设 , ,我们分唯一性和存在性两方面来证明.
唯一性:由 ,知 的导数等于 ,而 ,故 显然恒为负,
从而 在 上单调递减.
特别地, 在 上单调递减.
这表明,使得 的 至多有一个,从而唯一性得证.
存在性:我们先考虑函数 ,这里 . 由于 ,故当 时 ,
当 时 ,从而 在 上单调递减,在 上单调递增,从而对于任意的 ,
都有 ,即 .
这就得到,对任意 ,有 .
从而,对任意的 ,都有 ;而对任意的 ,都有 .
然后回到原题,首先我们有.
同时我们又有
,
,
故 .
由零点存在定理,知一定存在 ,使得 .
综合上述的存在性和唯一性两个方面,知存在唯一的 ,使得 .
【点睛】关键点点睛:本题的关键点在于,对于存在唯一性的证明,将唯一性和存在性分开论证,则证明
的逻辑会更加清晰,不易出现错误.
25.(2024·重庆·模拟预测)已知函数
(1)若过点 的直线与曲线 切于点 ,求 的值;
(2)若 有唯一零点,求 的取值范围.
【答案】(1)
(2) 或【分析】(1)先求 ,得到切点,再求导,求出 得到切线斜率,利用点斜式写出切线方程,再由
切线过点 ,可求 的值.
(2)根据参数 的不同取值范围,讨论函数的单调性,求出函数的极值,结合当 趋近于0时,函数值的
符号,又函数只有一个零点,就可以确定 的取值范围.
【详解】(1)由题可得 , , .
有 ,解得 .
(2)因为 ,
令 , , ,
, ,
由 ,所以 在 上递减,在 上递增..
所以 ,当 时 ,
(ⅰ)当 时, , ,
由 .
所以 在 上递减,在 上递增,当 时, , ,
当 时, ,所以 有1个零点.
(ⅱ)当 时,由 ,所以 在 上递减,在 上递增,
,
①若 , 有唯一零点.②若 , ,当 时, ,
当 时, ,所以 有2个零点,不合题意;
③若 , , 无零点,
(ⅲ)当 时,设 满足 ,
①若 , 在 上大于等于0,故有 单调递增,
,故有 唯一零点;
②若 , 在 递增,在 递减,在 递增,
, 有唯一零点;
③若 , 在 递增,在 递减,在 递增, , 有唯一
零点;
综上,若 有唯一零点,a的取值范围是 或 .
【点睛】方法点睛:已知函数有零点求参数取值范围常用的方法和思路:
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.
26.(2024·江苏南通·模拟预测)设函数 , .
(1)若 ,求函数 的单调区间;
(2)若 ,试判断函数 在区间 内的极值点的个数,并说明理由;
(3)求证:对任意的正数 ,都存在实数 ,满足:对任意的 , .【答案】(1)减区间 ,增区间
(2) 在 内有一个极值点
(3)证明见解析
【分析】(1)求解 ,利用 , ,解不等式求解单调递增区间,单调递减区间.
(2) ,其中 ,再次构造函数令 ,分析 的零点情况. ,
令 , ,列表分析得出 单调性,判断 ,由 ,可判断
的零点个数,即可判断 的极值点个数.
(3)先猜想 , 恒成立.再运用导数判断证明.令 , .
,求解最大值,得出 即可.
【详解】(1)当 时, , ,
令 , ,列表分析
1
0
单调递减 单调递增
故 的单调递减区间为 ,单调递增区间为 ;
(2) , ,其中 ,
令 , ,令 , ,
列表分析:0
单调递
单调递增
减
,
而 , , ,
若 ,则 , , ,
因此 在 上有一个零点,所以 在 内有一个极值点;
(3)猜想: , 恒成立.
证明如下:
由(2)得 在 上单调递增,且 , .
因为当 时, ,
所以 .
故 在 上存在唯一的零点,设为 .由
0
单调递减 单调递增
知, , ,
又 ,而 时, ,
所以 (1).
即 , .
所以对任意的正数 ,都存在实数 ,使对任意的 ,使 .
补充证明令 , . ,
所以 在 上单调递增.
所以 时, ,即 .
补充证明
令 , . ,
所以 在 上单调递减.
所以 时, ,即 .
【点睛】关键点点睛:本题第三问的关键是先猜想 , 恒成立,再运用导数判断证明,
对于存在性问题,找到一个可存在的情况进行证明.
27.(2024·河北保定·二模)已知函数 .
(1)若 ,求曲线 在点 处的切线方程;
(2)若 ,试讨论 的零点个数.
【答案】(1)
(2)答案见解析
【分析】(1)求得 的导数,可得切线斜率和切点,从而求得切线方程;
(2)由 为奇函数,将问题转化为讨论 在 上的零点,求得导数,讨论 , ,
和 ,求得 的单调性、极值和最值,结合零点存在定理,即可得到零点个数.
【详解】(1)当 时, , .
, .
故曲线 在点 处的切线方程为 .
(2)因为 ,所以 为奇函数.又因为 ,所以只需要讨论 在 上的零点.
, .
令函数 ,
①当 ,即 时,分段讨论:
当时 , .
当 时, ,所以 在 上单调递减,即 在 上单调递减
因为 , ,所以存在 ,使得 .
当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减.
因为 , ,所以 在 上有1个零点,
在 上有3个零点.
②当 ,即 时, , 在 上单调递减,
所以 在 上没有零点,在 上有1个零点.
③当 ,即 时,分段讨论:
当 时, .
当 时, ,所以 在 上单调递增,即 在 上单调递增.
因为 , ,所以存在 ,使得 .当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增.
因为 , ,
所以 在 上没有零点,在 上有1个零点.
④当 ,即 时,分段讨论:
当 时, .
当 时,令函数 ,
.
所以 在 上单调递增,即 在 上单调递增.
因为 , ,所以存在 ,使得 .
所以 在 上单调递减,在 上单调递增,
即在 在 上单调递减,在 上单调递增.
因为 , ,所以存在 ,使得 .
当时 , ,当 时, ,
所以 在 上单调递减,在 上单调递增.因为 , ,
所以 在 上没有零点,在 上有1个零点.
综上,当 时, 在 上有3个零点;
当 时, 在 上有1个零点.
【点睛】方法点睛:利用导数解决函数零点问题的方法:
(1)直接法:先对函数求导,根据导数的方法求出函数的单调区间与极值,根据函数的基本性质作出图
象,然后将问题转化为函数图象与 轴的交点问题,突出导数的工具作用,体现了转化与化归思想、数形
结合思想和分类讨论思想的应用;
(2)构造新函数法:将问题转化为研究两函数图象的交点问题;
(3)参变量分离法:由 分离变量得出 ,将问题等价转化为直线 与函数 的
图象的交点问题.
28.(2024·河北·二模)已知函数 .
(1)求曲线 在 处的切线 与坐标轴围成的三角形的周长;
(2)若函数 的图象上任意一点 关于直线 的对称点 都在函数 的图象上,且存在 ,使
成立,求实数 的取值范围.
【答案】(1)
(2)
【分析】(1)根据导数的几何意义求切线方程,进而求得 与 轴的交点与 轴的交点,计算可得结果;
(2)根据对称性求函数 的解析式,将问题转化为存在 ,使 成立,构造函数
,转化为函数的最值问题并求解.【详解】(1)由 ,得 ,
所以切线 的斜率 .
所以切线 的方程为 ,即 .
令 ,得 ,令 ,得 ,所以切线 与 轴交于点 ,与 轴交于点 ,
所以切线 与坐标轴围成的三角形的周长为 .
(2)设 ,则 ,
由题意知 在 的图象上,
所以 ,所以 .
由 ,
得 ,即 ,
因为存在 ,使 成立,所以存在 ,使 成立,
设 ,则 ,又 ,当且仅当 时等号成立,
所以 单调递增,
所以当 时, ,
可得 ,即实数 的取值范围是
29.(2024·河北邯郸·二模)已知函数 .
(1)是否存在实数 ,使得 和 在 上的单调区间相同?若存在,求出 的取值范围;若不存
在,请说明理由.
(2)已知 是 的零点, 是 的零点.
①证明: ,②证明: .
【答案】(1)存在,且
(2)①证明见解析 ②证明见解析
【分析】(1)结合导数与函数单调性的关系,分 与 进行讨论即可得;
(2)①利用导数得到 的单调性后,借助零点的存在性定理可得 ,解出即可得;
②构造函数 ,结合导数得到函数的单调性,画出相应图象,可得从而得
到 , ,从而可得 ,结合 的范围即可得解.
【详解】(1)由题意得 ,
当 时, ,所以 和 在 上都单调递增,符合题意;
当 时,若 和 在 上的单调区间相同,
则 和 有相同的极值点,即 ,
令 ,则 ,
当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,则 ,
所以 无解,
综上,当 时, 和 在 上的单调区间相同;
(2)①由题意, 有两个零点, ,
若 ,则 ,所以 在 上单调递增,不符合题意,
若 ,则当 时, 单调递减,当 时, 单调递增,
且当 时, ,当 时, ,
所以 ,解得 ,得证;
②令 ,得 ,即 ,
令 ,则 ,
当 时, 单调递减,
当 时, 单调递增,
当 时, 单调递减,
当 时, 单调递增,
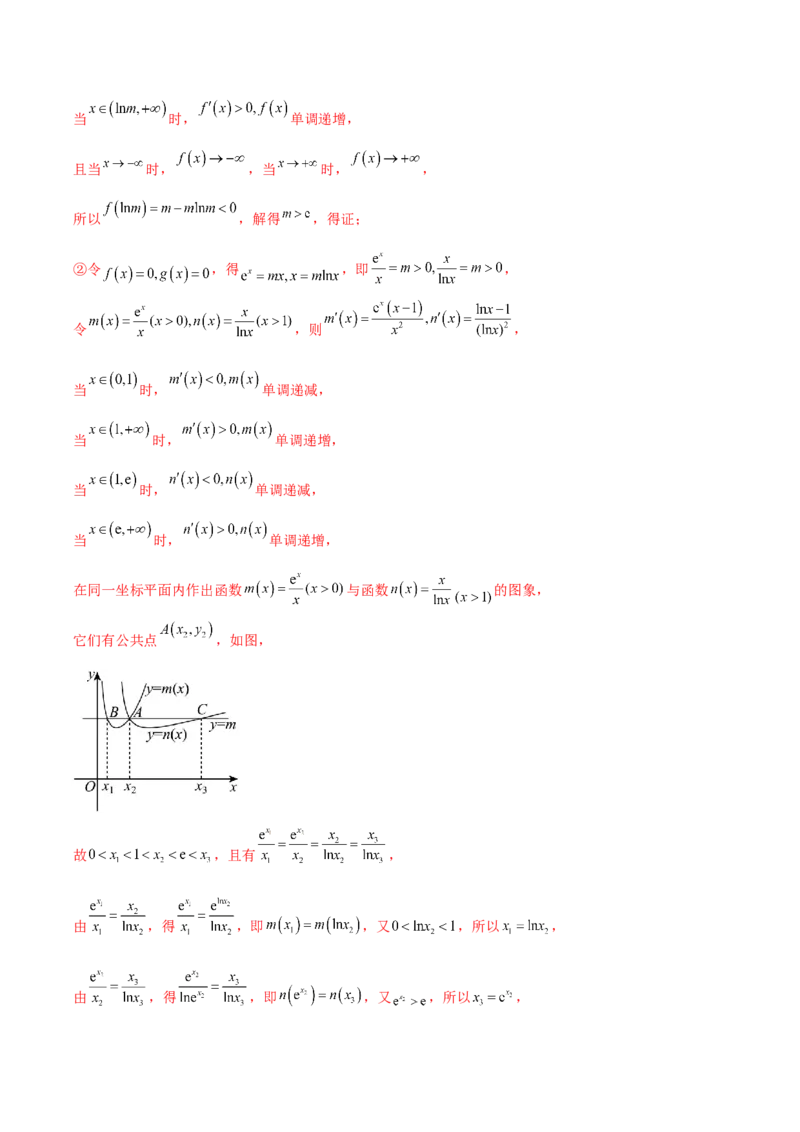
在同一坐标平面内作出函数 与函数 的图象,
它们有公共点 ,如图,
故 ,且有 ,
由 ,得 ,即 ,又 ,所以 ,
由 ,得 ,即 ,又 ,所以 ,由 ,得 ,即 ,
故 .
【点睛】关键点点睛:本题最后一问关键点在于构造函数 ,结合导数得
到函数的单调性,从而得到 .
30.(2024·浙江杭州·模拟预测)已知函数 .
(1)当 时,证明: ;
(2)当 时, ,求 的最大值;
(3)若 在区间 存在零点,求 的取值范围.
【答案】(1)证明见解析
(2)
(3)
【分析】(1)求定义域,作商法结合基本不等式比较出 ;
(2)对 求导,变形后,构造 ,求导,再构造 ,求导得到单调
性,结合 得到 的单调性和极值,最值情况,求出答案;
(3)令 ,当 时,由于 恒成立,故无解,当 时,
,令 , ,求导得到函数单调性,又 趋向于0时,趋向于2,故 ,从而得到 ,得到答案.
【详解】(1) 定义域为 ,
当 时, , ,
由于 ,
令 ,
当且仅当 ,即 时,等号成立,
又 ,故 ;
(2)当 时, ,
,
设 ,则 ,
令 ,
,
故 在 上单调递增,
又 ,故当 时, ,即 ,
即 ,故 ,所以 ,则 在 恒成立,
当 时,同理可得 ,则 在 上恒成立,
故 在 上单调递减,在 上单调递增,
故 在 处取得极小值,也是最小值, ,
故 ,所以 的最大值为 ;
(3) ,令 ,
当 时, ,由于 恒成立,故无解,舍去;
当 时, ,
令 , ,
,
下面证明 , ,
令 , ,则 , ,其中 ,
令 , ,则 , ,其中 ,
令 , ,则 , ,
当 时, ,故 在 上单调递增,
故 ,故 在 上单调递增,故 ,故 在 上单调递增,
故 ,即 , ,
则 , ,
则 ,
,
由于 ,而 ,故 ,
则 ,故 在 上单调递增,
又 趋向于0时, 趋向于2,故 ,
故令 ,解得 ,此时 有解,故存在零点,
故 的取值范围是 .
【点睛】方法点睛:对于求不等式成立时的参数范围问题,一般有三个方法,一是分离参数法, 使不等式
一端是含有参数的式子,另一端是一个区间上具体的函数,通过对具体函数的研究确定含参式子满足的条
件.二是讨论分析法,根据参数取值情况分类讨论,三是数形结合法,将不等式转化为两个函数,通过两个
函数图像确定条件.