文档内容
第七章 随机变量及其分布(提高卷)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间1200分钟,试题共23题.答卷前,考生务必用0.5毫米黑色签字笔将
自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共12小题,每小题5分,共60分)在每小题所给出的四个选项中,只有一项是符合
题目要求的.
1.随机变量X~B(4, ),则D(3X+1)等于( )
A. B. C.6 D.8
【答案】D
【分析】判断随机变量X的概率类型,利用二项分布求解方差,然后求解D(3X+1).
【解答】解:由二项分布的概念可知:n=4,p= ,则:D(X)=np(1﹣p)= = ,
D(3X+1)=32D(X)=9× =8.
故选:D.
【知识点】二项分布与n次独立重复试验的模型、离散型随机变量的期望与方差
2.设随机变量ξ的概率分布列为P(ξ=k)=a( )k,其中k=0,1,2,那么a的值为( )
A. B. C. D.
【答案】D
【分析】由已知分别求出P(ξ=0),P(ξ=1),P(ξ=2),由此利用离型随机变量的分布列的性质能求出
a的值.
【解答】解:∵随机变量ξ的概率分布列为P(ξ=k)=a( )k,其中k=0,1,2,
∴P(ξ=0)= =a,
P(ξ=1)=a( )= ,
P(ξ=2)=a( )2= ,
∴a+ =1,
解得a= .
故选:D.
【知识点】离散型随机变量及其分布列
3.从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A为“第一次取到的是奇数”,B为
“第二次取到的是3的整数倍”,则P(B|A)=( )
A. B. C. D.
【答案】B
【分析】先计算n(AB)、n(A),再利用P(B|A)= ,即可求得结论.
【解答】解:由题意,n(AB)= =13,n(A)= =40
∴P(B|A)= = .
故选:B.
【知识点】条件概率与独立事件
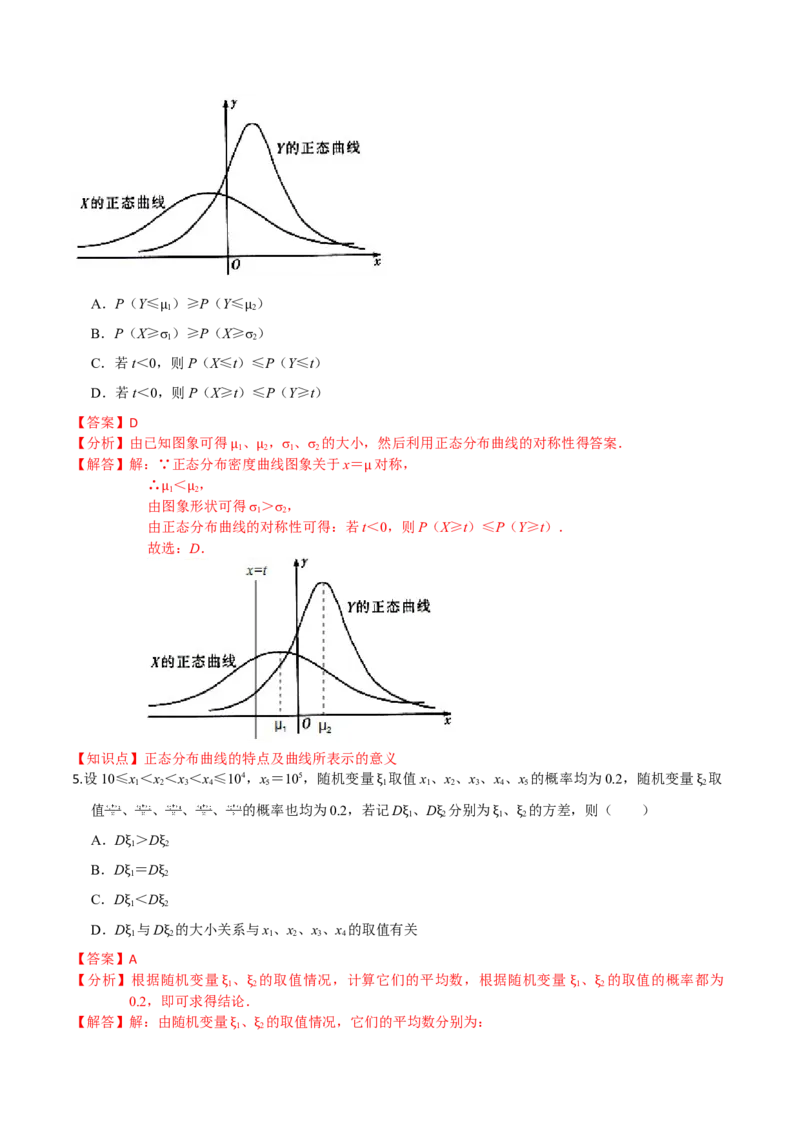
4.设X~N( ,σ2),Y~N( ,σ2),这两个正态曲线如图所示,下列说法正确的是( )
1 1 2 2
μ μA.P(Y≤ )≥P(Y≤ )
1 2
B.P(X≥μσ)≥P(X≥μσ)
1 2
C.若t<0,则P(X≤t)≤P(Y≤t)
D.若t<0,则P(X≥t)≤P(Y≥t)
【答案】D
【分析】由已知图象可得 、 ,σ、σ 的大小,然后利用正态分布曲线的对称性得答案.
1 2 1 2
【解答】解:∵正态分布密度曲线图象关于x= 对称,
μ μ
∴ < ,
1 2
μ
由图象形状可得σ>σ,
1 2
μ μ
由正态分布曲线的对称性可得:若t<0,则P(X≥t)≤P(Y≥t).
故选:D.
【知识点】正态分布曲线的特点及曲线所表示的意义
5.设10≤x <x <x <x≤104,x =105,随机变量 取值x 、x 、x 、x 、x 的概率均为0.2,随机变量 取
1 2 3 4 5 1 1 2 3 4 5 2
值 、 、 、 、 的概率也均为0.2,若记ξ D 、D 分别为 、 的方差,则( ) ξ
1 2 1 2
A.D 1 >D 2 ξ ξ ξ ξ
B.Dξ=Dξ
1 2
C.Dξ <Dξ
1 2
D.Dξ 与Dξ 的大小关系与x、x、x、x 的取值有关
1 2 1 2 3 4
【答案】ξA ξ
【分析】根据随机变量 、 的取值情况,计算它们的平均数,根据随机变量 、 的取值的概率都为
1 2 1 2
0.2,即可求得结论.
ξ ξ ξ ξ
【解答】解:由随机变量 、 的取值情况,它们的平均数分别为:
1 2
ξ ξ= (x+x+x+x+x ), = ( + + + + )= 且随机变量 、 的取值的概率都为
1 2 3 4 5 1 2
0.2,所以有D >D ,
1 2
ξ ξ
故选:A.
ξ ξ
【知识点】离散型随机变量及其分布列、离散型随机变量的期望与方差
6.设0<p<1,随机变量 的分布列是
ξ 0 1 2
Pξ
则当p在(0,1)内增大时,( )
A.D( )减小 B.D( )增大
C.D(ξ)先减小后增大 D.D(ξ)先增大后减小
【答案】Dξ ξ
【分析】求出随机变量 的分布列与方差,再讨论D( )的单调情况.
【解答】解:设0<p<1,随机变量 的分布列是
ξ ξ
E( )=0× +1× +2× =p+ ;
ξ
方差是D( )= × + × + ×
ξ
=﹣p2+p+
ξ
=﹣ + ,
∴p (0, )时,D( )单调递增;
p ( ,1)时,D( )单调递减;
∈ ξ
∴D( )先增大后减小.
∈ ξ
故选:D.
ξ
【知识点】离散型随机变量的期望与方差
7.如图,《宋人扑枣图轴》是作于宋朝的中国古画,现收藏于中国台北故宫博物院,有甲、乙两人想根据
该图编排一个舞蹈,舞蹈中他们要模仿该图中小孩扑枣的爬、扶、捡、顶中的两个动作,每人模仿一
个动作,若他们采用抽签的方式来决定谁模仿哪个动作,则甲只能模仿“爬”或“扶”且乙只能模仿
“扶”或“检”的概率是( )
A. B. C. D.
【答案】C
【分析】基本事件总数n=4×4=16,甲只能模仿“爬”或“扶”且乙只能模仿“扶”或“捡”包含的基
本事件个数m=2×2=4,由此能求出甲只能模仿“爬”或“扶”且乙只能模仿“扶”或“捡”的
概率.
【解答】解:甲、乙两人模仿小孩扑枣的爬、扶、捡、顶中的两个动作,两人每人模仿一个动作.
他们采用抽签的方式来决定谁模仿哪个动作,
基本事件总数n=4×4=16,甲只能模仿“爬”或“扶”且乙只能模仿“扶”或“捡”包含的基本事件个数:
m=2×2=4,
则甲只能模仿“爬”或“扶”且乙只能模仿“扶”或“捡”的概率是P= = = .
故选:C.
【知识点】相互独立事件和相互独立事件的概率乘法公式
8.某商场经营的某种包装的大米质量 (单位:kg)服从正态分布N(10,σ2),根据检测结果可知P
(9.9≤ ≤10.1)=0.96,某公司为每ξ 位职工购买一袋这种包装的大米作为福利,若该公司有 1000名职
工,则分ξ 发到的大米质量在9.9kg以下的职工数大约为( )
A.10 B.20 C.30 D.40
【答案】B
【分析】根据大米质量 服从正态分布 N(10,σ2).得到大米质量 关于 =10 对称,根据 P
(9.9≤ ≤10.1)=0.96,得到P( <9.9)=0.02,根据频率乘以样本容量得到分发到的大米质
ξ ξ ξ
量在9.9kg以下的职工数.
ξ ξ
【解答】解:∵大米质量 服从正态分布N(10,σ2).
∴大米质量 关于 =10对称,
ξ
∵P(9.9≤ ≤10.1)=0.96,
ξ ξ
∴P( <9.9)= =0.02,
ξ
∴公司有1000名职工,则分发到的大米质量在9.9kg以下的职工数大约为0.02×1000=20.
ξ
故选:B.
【知识点】正态分布曲线的特点及曲线所表示的意义
9.设一个正三棱柱ABC﹣DEF,每条棱长都相等,一只蚂蚁从上底面ABC的某顶点出发,每次只沿着棱爬
行并爬到另一个顶点,算一次爬行,若它选择三个方向爬行的概率相等,若蚂蚁爬行10次,仍然在上
底面的概率为P ,则P 为( )
10 10
A. B.
C. D.
【答案】D
【分析】根据题意假设蚂蚁爬n次仍在上底面的概率为P,那么它前一步只有两种情况:也许本来就在上
n
底面,再走一步要想不掉下去,只有两条路,其概率是 P ;也许是上一步在下底面,则第n﹣
n﹣1
1步不再上底面的概率是1﹣P ,如果爬上来,其概率应是 (1﹣P ).两件事情是互斥的,
n﹣1 n﹣1
因此,P = P + (1﹣P ),整理得,P = P + ;构造等比数列{P﹣ },即可得P = ( )
n n﹣1 n﹣1 n n﹣1 n n
n+ .
【解答】解:设蚂蚁爬n次仍在上底面的概率为P,那么它前一步只有两种情况:
n
A:如果本来就在上底面,再走一步要想不掉下去,只有两条路,其概率是 P ;
n﹣1
B:如果是上一步在下底面,则第n﹣1步不再上底面的概率是1﹣P ,如果爬上来,其概率
n﹣1
应是 (1﹣P ).
n﹣1
A,B事件互斥,因此,P= P + (1﹣P );
n n﹣1 n﹣1
整理得,P= P + ;即P﹣ = (P ﹣ );
n n﹣1 n n﹣1
构造等比数列{P﹣ },公比为 ,首项为P﹣ = ﹣ = ,
n 1
可得P= ( )n+ .
n
因此第10次仍然在上底面的概率P = ( )10+ .
10故选:D.
【知识点】n次独立重复试验中恰好发生k次的概率
10.随机变量 的分布列如下:
ξ n n+1 n+2
Pξ a b c
其中a,b,c成等差数列,则D( )( )
A.与n有关,有最大值 ξ B.与n有关,有最小值
C.与n无关,有最大值 D.与n无关,有最小值
【答案】C
【分析】求出D( )的表达式,分析其与n的关系,求最值即可.
【解答】解:依题意,a+c=2b,a+b+c=1,所以b= ,
ξ
E( )=na+(n+1)b+(n+2)c=n(a+b+c)+b+2c﹣=n+b+2c.
E( 2)=n2a+(n+1)2b+(n+2)2c,
ξ
所以D( )=E( 2)﹣E2( )=n2a+(n+1)2b+(n+2)2c﹣(n+b+2c)2=)﹣4 ,(0
ξ
),
ξ ξ ξ
所以D( )与n无关,且当c= 时,D( )有最大值 .
故选:C.
ξ ξ
【知识点】离散型随机变量的期望与方差
11.一台机器在一天内发生故障的概率为0.1,若这台机器一周5个工作日不发生故障,可获利4万元;发
生1次故障获利为0万元;发生2次或2次以上故障要亏损1万元,这台机器一周5个工作日内可能获
利的数学期望是( )万元.(已知0.94=0.6561,0.95=0.5905)
A.3.4736 B.3 C.2.2805 D.1.231
【答案】C
【分析】先由概率公式求出一周内机器发生故障的次数 的概率,由题意知 =0,1,2次及以上分别对应
的利润是4,0,﹣1万元,由求期望的公式求出即可.
ξ ξ
【解答】解:以 表示一周内机器发生故障的次数,则 ~B(5,0.1),
∴P( =k)=C k×0.1k×0.95﹣k(k=0、1、…、5),
5
ξ ξ
以 表示一周内获得的利润,则 =g( ),
ξ
而g(0)=4,g(1)=0,g( ≥2)=﹣1
η η ξ
∴P( =5)=P( =0)=0.95=0.59049,
ξ
P( =0)=P( =1)=C 1×0.11×0.94=0.32805,
5
η ξ
P( =﹣1)=P( ≥2)=C 2×0.12×0.93+C 3×0.13×0.92+C 4×0.14×0.9+C 5×0.15=0.08146,
5 5 5 5
η ξ
∴E =4×0.59049+0×0.32805﹣0.08146=2.2805.
η ξ
这台机器一周内可获利的均值是 2.2805万元.
η
故选:C.
【知识点】离散型随机变量的期望与方差
12.1654年,法国贵族德•梅雷骑士偶遇数学家布莱兹•帕斯卡,在闲聊时梅雷谈了最近遇到的一件事:某
天在一酒吧中,肖恩和尤瑟纳尔两人进行角力比赛,约定胜者可以喝杯酒,当肖恩赢20局且尤瑟纳尔
赢得40局时他们发现桌子上还剩最后一杯酒.此时酒吧老板和伙计提议两人中先胜四局的可以喝最后那杯酒,如果四局、五局、六局、七局后可以决出胜负那么分别由肖恩、尤瑟纳尔、酒吧伙计和酒吧
老板付费,梅雷由于接到命令需要觐见国王,没有等到比赛结束就匆匆离开了酒馆.请利用数学知识
做出合理假设,猜测最后付酒资的最有可能是( )
A.肖恩 B.尤瑟纳尔 C.酒吧伙计 D.酒吧老板
【答案】B
【分析】由题意可得,肖恩每局获胜的概率为 ,尤瑟纳尔每局获胜的概率为 ,先胜四场比赛意味着比赛
采用七局四胜制,设决出胜负的场数为X,求出P(X=4),P(X=7),P(X=6),P(X=
5)的值,并比较大小,即可判断出结果.
【解答】解:由题意可得,肖恩每局获胜的概率为 = ,尤瑟纳尔每局获胜的概率为 = ,
先胜四场比赛意味着比赛采用七局四胜制,设决出胜负的场数为X,
则P(X=4)= + = ,
P(X=5)= = ,
P(X=6)= + × + = ,
P(X=7)= = ,
∵ ,
∴P(X=4)<P(X=7)<P(X=6)<P(X=5),
∴ 最后付酒资的最有可能是尤瑟纳尔.
故选:B.
【知识点】相互独立事件和相互独立事件的概率乘法公式、独立性检验
二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线
上)
13.已知随机变量X服从正态分布N(3,1),且P(X<2c+2)=P(X>c+4),则c= .
【答案】0
【分析】根据正态曲线关于x=3对称,得到两个概率相等的区间关于x=3对称,得到关于c的方程,解
方程即可.
【解答】解:∵随机变量 服从正态分布N(3,1),P(X<2c+2)=P(X>c+4),
∴2c+2+c+4=6,
ξ
∴c=0,
故答案为:0.
【知识点】正态分布曲线的特点及曲线所表示的意义
14.某地区气象台统计,该地区下雨的概率是 ,刮风的概率为 ,既刮风又下雨的概率为 ,设A为下雨,B
为刮风,那么P(B|A)等于 .
【分析】代入条件概率公式计算.
【解答】解:由题意可知p(AB)= ,P(A)= ,
∴P(B|A)= = .
故答案为: .
【知识点】条件概率与独立事件15.若离散型随机变量X的分布列为
X 1 0
P 2a a
则常数a= ,X的数学期望E(X)= .
【分析】由离散型随机变量X的分布列,得2a+a=1,由此能求出常数a和E(X).
【解答】解:由离散型随机变量X的分布列,得:
2a+a=1,解得a= ,
E(X)= = .
故答案为: ,
【知识点】离散型随机变量及其分布列
16.某校举行知识比赛,比赛分为初赛和复赛两部分,初赛采用选手从备选题中选一题答 一题的方式进行
每位选手最多有 5 次答题机会,选手累计答对 3 题或答错 3 题即终止比赛,答对 3 题者直接进入
复赛,答错 3 题 者则被淘汰.已知选手甲答对每题的概率均 ,且相互之间没有影响,则选手甲进入
复赛的概率是 .
【分析】利用n次独立试验中事件A恰好发生k次的概率计算公式能求出选手甲进入复赛的概率.
【解答】解:∵选手甲答对每题的概率均 ,
每位选手最多有5 次答题机会,选手累计答对3 题或答错3 题即终止比赛,
答对 3 题者直接进入复赛,答错 3 题 者则被淘汰,
∴选手甲进入复赛的概率是:
p= + = .
故答案为: .
【知识点】相互独立事件和相互独立事件的概率乘法公式
三、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过
程或演算步骤)
17.某中学高中毕业的三名同学甲、乙、丙参加某大学的自主招生考核,在本次考核中只有合格和优秀两
个等次,若考核为合格,则给子10分的降分资格:若考核为优秀,则给予20分的降分资格.假设甲、
乙、丙考核为优秀的概率分别为 、 、 ,他们考核所得的等次相互独立.
(Ⅰ)求在这次考核中,甲、乙、丙三名同学中至少有一名考核为优秀的概率.
(Ⅱ)记在这次考核中.甲、乙、丙三名同学所得降分之和为随机变量 X,写出X所有可能的取值,并求
P(X≥50)的值.
【分析】(Ⅰ)利用相互独立事件概率乘法公式和对立事件概率计算公式能求出在这次考核中,甲、乙、
丙三名同学中至少有一名考核为优秀的概率.
(Ⅱ)记在这次考核中.甲、乙、丙三名同学所得降分之和为随机变量X,则X所有可能的取
值为30,40,50,60,利用相互独立事件概率乘法公式和互斥事件概率计算公式能求出 P(X≥50).
【解答】解:(Ⅰ)某中学高中毕业的三名同学甲、乙、丙参加某大学的自主招生考核,
在本次考核中只有合格和优秀两个等次,
若考核为合格,则给子10分的降分资格:若考核为优秀,则给予20分的降分资格.
假设甲、乙、丙考核为优秀的概率分别为 、 、 ,他们考核所得的等次相互独立.
∴在这次考核中,甲、乙、丙三名同学中至少有一名考核为优秀的概率:
P=1﹣(1﹣ )(1﹣ )(1﹣ )= .
(Ⅱ)记在这次考核中.甲、乙、丙三名同学所得降分之和为随机变量X,
则X所有可能的取值为30,40,50,60,
P(X=50)= + +(1﹣ )× = ,
P(X=60)= = ,
∴P(X≥50)=P(X=50)+P(X=60)= = .
【知识点】相互独立事件和相互独立事件的概率乘法公式
18.某校从学生文艺部6名成员(4男2女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
【分析】(1)求出基本事件的总数以及符合条件的个数,即可求解结论;
(2)根据条件概率的公式求解即可;
(3)分别求出各自对应的概率,再代入条件概率的计算公式求解即可.
【解答】解:(1)从6名成员中挑选2名成员,共有15种情况,记“男生甲被选中”为事件 A,事件A
所包含的基本事件数为5种,故 .
(2)记“男生甲被选中”为事件A,“女生乙被选中”为事件B,则 ,由(1)知 ,故
.
(3)记“挑选的2人一男一女”为事件C,则 ,“女生乙被选中”为事件B, ,故
.
【知识点】古典概型及其概率计算公式、条件概率与独立事件
19.某工厂加工某种零件需要经过A,B,C三道工序,且每道工序的加工都相互独立,三道工序加工合格
的概率分别为p, , .三道工序都合格的零件为一级品;恰有两道工序合格的零件为二级品;其它均
为废品,且加工一个零件为二级品的概率为 .
(1)求p;
(2)若该零件的一级品每个可获利200元,二级品每个可获利100元,每个废品将使工厂损失50元,设
一个零件经过三道工序加工后最终获利为X元,求X的分布列及数学期望.
【分析】(1)设零件经A,B,C三道工序加工合格的事件分别记为A,B,C,设事件D为“生产一个零
件为二级品”,则P(D)=(1﹣p)× = ,由此能求出p.
(2)X的可能取值为200,100,﹣50,分别求出相应的概率,由此能求出X的分布列、EX.
【解答】解:(1)设零件经A,B,C三道工序加工合格的事件分别记为A,B,C,
则p(a)=p,P(B)= ,P(C)= ,P(A)=1﹣p,P(B)= ,P(C)= .
设事件D为“生产一个零件为二级品”,由已知A,B,C是相互独立事件,
则P(D)=(1﹣p)× = ,解得p= .
(2)X的可能取值为200,100,﹣50,
P(X=200)= ,
P(X=100)= ,
P(X=﹣50)=1﹣ = ,
则X的分布列为
X 200 100 ﹣50
P
所以EX=200× = .
【知识点】相互独立事件和相互独立事件的概率乘法公式、离散型随机变量的期望与方差、离散型随机变
量及其分布列
20.某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按 200元/次收费,并注册成为
会员,对会员的后续体检给予相应优惠,标准如下:
体检次序 第一次 第二次 第三次 第四次 第五次及以上
收费比例 1 0.95 0.90 0.85 0.8
该休检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如表:
检次数 一次 两次 三次 四次 五次及以上
频数 60 20 12 4 4
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(Ⅰ)已知某顾客在此体检中心参加了3次体检,求这3次体检,该体检中心的平均利润;
(Ⅱ)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出5人,再从
这5人中抽取2人,每人发放现金200元.用5表示体检3次的会员所得现金和,求 的分布列及E
( ). ξ
【ξ分析】(I)根据题意求出即可;
(II)利用分层抽样求出5个人中3人体检三次,1人体检四次,1人体验5次及以上, =0,
200,400,求出分布列和期望即可.
ξ
【解答】解:(1)医院3次体检的收入为200×(1+0.95+0.9)=570,
三次体验的成本为150×3=450,
故平均利润为(570﹣450)÷3=40元;
(2)根据题意抽取的5个人中3人体检三次,1人体检四次,1人体验5次及以上,
=0,200,400,
P( =0)= ,
ξ
P( =200)= .
ξ
P( =400)= ,
ξ
分布列如下:
ξ
0 200 400
ξP 0.1 0.6 0.3E( )=0+200×0.6+400×0.3=120+120=240.
【知识点】离散型随机变量的期望与方差、离散型随机变量及其分布列
ξ
21.某中学有学生500人,学校为了解学生的课外阅读时间,从中随机抽取了 50名学生,获得了他们某一
个月课外阅读时间的数据(单位:小时),将数据分为5组:[10,12),[12,14),[14,16),
[16,18),[18,20],整理得到如图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中的x的值;
(Ⅱ)试估计该校所有学生中,课外阅读时间不小于16小时的学生人数;
(Ⅲ)已知课外阅读时间在[10,12)的样本学生中有3名女生,现从阅读时间在[10,12)的样本学生中
随机抽取3人,记X为抽到女生的人数,求X的分布列与数学期望E(X).
【分析】(Ⅰ)利用频率分布直方图,通过概率和为1,即可求解x=0.15.
(Ⅱ)利用分布直方图求解即可.
(Ⅲ)随机变量X的所有可能取值为0,1,2,3,求出概率得到分布列,然后求解期望.
【解答】(共13分)
解:(Ⅰ)由0.05×2+0.08×2+0.10×2+0.12×2+2x=1,
可得x=0.15…(3分)
(Ⅱ)0.10×2+0.05×2=0.30,
即课外阅读时间不小于16个小时的学生样本的频率为0.30.500×0.30=150,
所以可估计该校所有学生中,课外阅读时间不小于16个小时的学生人数为150.
…(6分)
(Ⅲ)课外阅读时间在[10,12)的学生样本的频率为0.08×2=0.16,50×0.16=8,即阅读时间在
[10,12)的学生样本人数为8,
8名学生为3名女生,5名男生,
随机变量X的所有可能取值为0,1,2,3, ; ; ; .
所以X的分布列为:
X 0 1 2 3
P
故X的期望 …(13分)
【知识点】离散型随机变量的期望与方差、离散型随机变量及其分布列
22.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了
解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了 100人,发现样本中
A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:(0,1000] (1000,2000] 大于2000
仅使用A 18人 9人 3人
仅使用B 10人 14人 1人
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000
元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发
现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大
于2000元的人数有变化?说明理由.
【分析】(Ⅰ)从全校所有的1000名学生中随机抽取的100人中,A,B两种支付方式都不使用的有5人,
仅使用A的有30人,仅使用B的有25人,从而A,B两种支付方式都使用的人数有40人,由此
能求出从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率.
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金
额大于1000元的人数,则X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的
分布列和数学期望E(X).
(Ⅲ)从样本仅使用A的学生有30人,其中27人月支付金额不大于2000元,有3人月支付
金额大于2000元,随机抽查3人,发现他们本月的支付金额都大于2000元的概率为p= =
,不能认为认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化.
【解答】解:(Ⅰ)由题意得:
从全校所有的1000名学生中随机抽取的100人中,
A,B两种支付方式都不使用的有5人,
仅使用A的有30人,仅使用B的有25人,
∴A,B两种支付方式都使用的人数有:100﹣5﹣30﹣25=40,
∴从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率p= =
0.4.
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金
额大于1000元的人数,
则X的可能取值为0,1,2,
样本仅使用A的学生有30人,其中支付金额在(0,1000]的有18人,超过1000元的有12人,
样本仅使用B的学生有25人,其中支付金额在(0,1000]的有10人,超过1000元的有15人,
P(X=0)= = = ,
P(X=1)= = = ,
P(X=2)= = = ,
∴X的分布列为:
X 0 1 2
P
数学期望E(X)= =1.
(Ⅲ)不能认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化,理由如下:
从样本仅使用A的学生有30人,其中27人月支付金额不大于2000元,有3人月支付金额大
于2000元,
随机抽查3人,发现他们本月的支付金额都大于2000元的概率为p= = ,
虽然概率较小,但发生的可能性为 .
故不能认为认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化.
【知识点】离散型随机变量的期望与方差、离散型随机变量及其分布列