文档内容
第七章 随机变量及其分布(能力提升)B 卷
姓名: 班级:
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符
合题目要求的。
1.若随机变量 ,且 ,则 ( )。
A、
B、
C、
D、
2.设随机变量 、 ,若 ,则 ( )。
A、
B、
C、
D、
3.设 ,则随机变量 的分布列是:
则当 在 内增大时( )。
A、 增大
B、 减小
C、 先增大后减小
D、 先减小后增大
4.两位教师和两位学生排成一排拍合照,记 为两位学生中间的教师人数,则 ( )。
A、
B、
C、D、
5.在如图所示的正方形中随机投掷 个点,则落入阴影部分(曲线 为正态分布 的密度曲
线)的点的个数的估计值为( )。
A、
B、
C、
D、
注 : , ,
。
6.体育课的排球发球项目考试的规则是:每位学生最多可发球 次,一旦发球成功,则停止发球,否则一
直发到 次为止。设学生一次发球成功的概率为 ( ),发球次数为 ,若 的均值 ,
则 的取值范围是( )。
A、
B、
C、
D、
7. 年 月 日,第六届世界互联网大会发布了 项“世界互联网领先科技成果”,其中有 项成果
均属于芯片领域。现有 名学生从这 项“世界互联网领先科技成果”中分别任选 项进行了解,且学生
之间的选择互不影响,则恰好有 名学生选择“芯片领域”的概率为( )。
A、
B、
C、
D、
8.为加快新冠肺炎检测效率,某检测机构采取合并检测法,即将多人的拭子样本合并检测,若为阴性,
则可以确定所有样本都是阴性的,若为阳性,则还需要对本组的每个人再做检测。现对 名密切接触者的
拭子样本进行合并检测,每份样本的检测结果是阴性还是阳性都是相互独立的,每人检测结果呈阳性的概
率为 ,且检测次数的数学期望为 ,则 的值为( )。
A、B、
C、
D、
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。
9.掷一枚均匀的硬币两次,记事件 “第一次出现正面”, “第二次出现反面”,则有( )。
A、 与 相互独立
B、
C、 与B互斥
D、
10.下列说法中正确的是( )。
A、设随机变量 服从二项分布 ,则
B、已知随机变量 服从正态分布 且 ,则
C、 且
D、已知随机变量 满足 、 ,若 ,则 随着 的增大而减小,
随着 的增大而增大
11.下列命题中,正确的是( )。
A、已知随机变量服从二项分布 ,若 、 ,则
B、已知 、 ,则
C、设随机变量 服从正态分布 ,若 ,则
D、某人在 次射击中,击中目标次数为 , ,则当 时概率最大
12.如果知道事件 已发生,则该事件所给出的信息量称为“自信息”。设随机变量 的所有可能取值为
、 、...、 ,且 ( ), ,定义 的“自信息”为
。一次掷两个骰子,若事件 为“仅出现一个 ”,事件 为“至少出现一个 ”,
事件 为“出现的两个数之和是偶数”,则( )。
A、当 时,“自信息”
B、当 时,
C、事件 的“自信息”D、事件 的“自信息” 大于事件 的“自信息”
三、填空题:本题共4小题,每小题5分,共20分。
13.李明参加中央电视台《同一首歌》大会的青年志愿者选拔,在已知备选的 道题中,李明能答对其中
的 道,规定考试从备选题中随机地抽出 题进行测试,至少答对 题才能入选。则李明入选的概率为
。
14.某群体中的每位成员使用移动支付的概率都为 ,各成员的支付方式相互独立,设 为该群体的 位
成员中使用移动支付的人数, , ,则 。
15.随着电商的兴起,物流快递的工作越来越重要了,早在周代,我国便已出现快递制度,据《周礼·秋
官》记载,周王朝的官职中设置了主管邮驿,物流的官员“行夫”,其职责要求是“虽道有难,而不时必
达”。现某机构对国内排名前五的 家快递公司的某项指标进行了 轮测试(每轮测试的客观条件视为相
同),每轮测试结束后都要根据该轮测试的成绩对这 家快递公司进行排名,那么跟测试之前的排名比较,
这 轮测试中恰好有 轮测试结果都出现 家公司排名不变的概率为 。
16.设口袋中有黑球、白球共 个,从中任取 个球,已知取到白球个数的数学期望值为 ,则口袋中白球
的个数为 。
四、解答题:本题共6小题,共70分。应写出文字说明、证明过程或演算步骤。
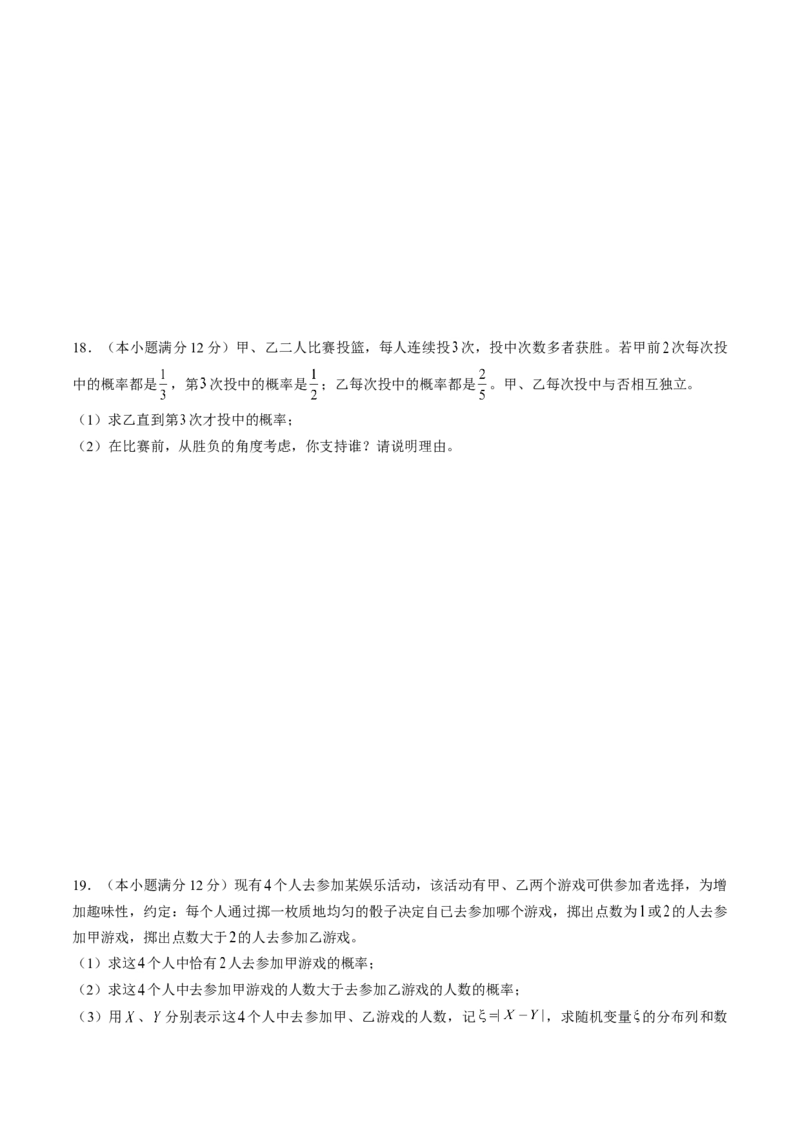
17. (本小题满分10分)如图是某市 月 日至 日的空气质量指数趋势图。空气质量指数小于 表示
空气质量优良,空气质量指数大于 ,表示空气重度污染。该市某校准备举行为期 天(连续 天)的运
动会,在 月 日至 月 日任意选定一天开幕。
(1)求运动会期间未遇到空气重度污染的概率;
(2)记运动会期间,空气质量优良的天数为 ,求随机变量 的分布列和均值。18.(本小题满分12分)甲、乙二人比赛投篮,每人连续投 次,投中次数多者获胜。若甲前 次每次投
中的概率都是 ,第 次投中的概率是 ;乙每次投中的概率都是 。甲、乙每次投中与否相互独立。
(1)求乙直到第 次才投中的概率;
(2)在比赛前,从胜负的角度考虑,你支持谁?请说明理由。
19.(本小题满分12分)现有 个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增
加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自已去参加哪个游戏,掷出点数为 或 的人去参
加甲游戏,掷出点数大于 的人去参加乙游戏。
(1)求这 个人中恰有 人去参加甲游戏的概率;
(2)求这 个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用 、 分别表示这 个人中去参加甲、乙游戏的人数,记 ,求随机变量 的分布列和数学期望。
20.(本小题满分12分)某钢管生产车间生产一批钢管,质检员从中抽出着十根对其直径(单位: )
进行测量,得出这批钢管的直径 服从正态分布 。
(1)当质检员随机抽检时,测得一根钢管的直径为 ,他立即要求停止生产,检查设备,请你根据所
学知识,判断该质检员的决定是否有道理,并说明判断的依据;
(2)如果钢管的直径 满足 为合格品(合格品的概率精确到 ),现要从 根
该种钢管中任意挑选 根,求次品数 的分布列和数学期望。
( 给 出 参 考 数 据 : 若 , 则 ,
, )。21.(本小题满分12分)个人所得税起征点是个人所得税工薪所得减除费用标准或免征额,个税起征点与
个人税负高低的关系最为直接,因此成为广大工薪阶层关注的焦点。随着我国人民收入的逐步增加,国家
税务总局综合考虑人民群众消费支出水平增长等各方面因素,规定从 年 月 日起,我国实施个税新
政。实施的个税新政主要内容包括:①个税起征点为 元;②每月应纳税所得额(含税) 收入-个税
起征点-专项附加扣除;③专项附加扣除包括住房、子女教育和赡养老人等。新旧个税政策下每月应纳税所
得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点 元) 新个税税率表(个税起征点 元)
每月应纳税所得额(含税) 每月应纳税所得额(含税)
缴税级数 税率/ 税率/
收入-个税起征点 收入-个税起征点-专项附加扣除
1 不超过 元部分 3 不超过 元部分
2 超过 元至 元部分 10 超过 元至 元部分
超过 元至 元的部
3 超过 元至 元的部分 20
分
超过 元至 元的部 超过 元至 元的部
4 25
分 分
5 超过 元至 元部分 30 超过 元至 元部分
… … … … …
随机抽取某市 名同一收入层级的无亲属关系的男性互联网从业者(以下互联网从业者都是指无亲
属关系的男性)的相关资料,经统计分析,预估他们 年的人均月收入为 元。统计资料还表明,
他们均符合住房专项扣除,同时他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合
子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除
但不符合子女教育扣除、既符合子女教育扣除又符合赡养老人扣除的人数之比是 。此外,
他们均不符合其他专项附加扣除。新个税政策下该市的专项附加扣除标准为:住房 元/月,子女教育
每孩 元/月,赡养老人 元/月等。
假设该市该收入层级的互联网从业者都独自享受专项附加扣除,将预估的该市该收入层级的互联网从
业者人均收入视为其个人月收入。根据样本估计总体的思想,解决下列问题。
(1)按新个税方案,设该市该收入层级的互联网从业者 年月缴个税为 元,求 的分布列和数学期
望;
(2)根据新旧个税方案,估计从 年 月开始,经过几个月,该市该收入层级的互联网从业者各月少
缴的个税之和就能购买一台价值 元的华为智慧屏巨幕电视。22.(本小题满分12分) 新型冠状病毒引发的疫情被世界卫生组织列为国际关注的突发公共卫生事
件。这种病毒可以通过飞沫进行传播,具有较强的传染性,由此导致大量的疑似病例产生,目前医院主要
采用核酸检测法来判断疑似病例是否真的感染这种病毒。假定疑似病例中随机 人检测结果呈阳性的概率
为 ,且每个人检测是否呈阳性相互独立。有人提出建议,利用分组检测法可有效减少工作量,具体
操作如下:将需要检测的疑似病例随机等分成若干组,并将每组送检的样本混在一起检测(假设样本混合
后不影响原有样本检测的结果),若结果呈阴性,则可断定本组样本全部为阴性,不必再检测;若结果呈
阳性,则本组中至少有一个样本呈阳性,再逐个检测。
(1)某医院每天要完成 个疑似病例的样本检測,现有两个分组方案:
方案一:将 人分成 组,每组 人,
方案二:将 人分成 组,每组 人,
试分析哪一个方案工作量更少;
(2)你能否给第(1)问中的医院提供一个更加合理的方案,并说明理由。