文档内容
蚌埠市 2024届高三年级第三次教学质量检查考试
数 学
本试卷满分150分,考试时间120分钟
注意事项:
1答卷前,务必将自己的姓名和座位号填写在答题卡和试卷上。
2回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,务必擦净后再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试
卷上无效。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题
目要求的。
1已知集合A={1,3,5,7,9},B={3,6,9,12},则A∩B=
A{3,9} B{1,3,5,6,7,9,12}
C{1,5,7} D{6,12}
2已知平面向量a=(1,m),b=(-2,4),且a∥b,则m=
1 1
A2 B C- D-2
2 2
x2 y2
3已知曲线C∶ + =1(m≠0),则“m∈(0,4)”是“曲线C的焦点在x轴上”的
4 m
A充分不必要条件 B必要不充分条件
C充要条件 D既不充分也不必要条件
槡2
4在△ABC中,角A,B,C的对边分别为a,b,c,已知a=acosB+bcosA=1,sinC= ,则
2
Ab=1 Bb=槡2 Cc=槡2 Dc=槡3
{S}
5记数列{a}的前n项和为S,若 n 是等差数列,S=-8,S=0,则a+a=
n n n 2 6 3 4
A-8 B-4 C0 D4
6(1-x+x2)2·(1+x)3的展开式中,x4的系数为
A1 B2 C4 D5
4
7在一组样本数据中,1,2,3,4出现的频率分别为 p,p,p,p,且∑p=1,则下面四种情形
1 2 3 4 i
i=1
中,对应样本的标准差最小的一组是
Ap=01,p=02,p=03,p=04 Bp=04,p=03,p=02,p=01
1 2 3 4 1 2 3 4
Cp=p=01,p=p=04 Dp=p=04,p=p=01
1 4 2 3 1 4 2 3
8已知抛物线C∶y2=4x,过其焦点F的直线交 C于 A,B两点,M为 AB中点,过 M作准线的
垂线,垂足为N,若|AF|=4,则|NF|=
4 4槡3 8 8槡3
A B C D
3 3 3 3
蚌埠市高三年级数学试卷第1页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}
书书书二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得6分,部分选对的得部分分,有选错的得0分。
( π) (π π)
9已知函数f(x)=sinωx- (ω>0)在区间 , 上单调递增,则ω的值可以是
6 6 2
2 4 3
A B1 C D
3 3 2
10科学研究表明,物体在空气中冷却的温度变化是有规律的如果物体的初始温度为 θ℃,
1
空气温度θ℃保持不变,则t分钟后物体的温度 θ(单位:℃)满足:θ=θ+(θ-θ)e-005t
0 0 1 0
若空气温度为10℃,该物体温度从θ℃(90≤θ≤100)下降到30℃,大约所需的时间为 t,
1 1 1
若该物体温度从 70℃,50℃下降到 30℃,大约所需的时间分别为 t,t,则(参考数据:
2 3
ln2≈07,ln3≈11)
At=20 B28≤t≤30 Ct≥2t Dt-t≤6
2 1 1 3 1 2
11已知正方体ABCD-ABCD 棱长为4,点 N是底面正方形 ABCD内及边界上的动点,点
1 1 1 1
M是棱DD 上的动点(包括点D,D),已知MN=4,P为MN中点,则下列结论正确的是
1 1
A无论M,N在何位置,AP,CC为异面直线
1
槡3
B若M是棱DD 中点,则点P的轨迹长度为 π
1 2
CM,N存在唯一的位置,使AP∥平面ABC
1 1
1
DAP与平面ABCD 所成角的正弦最大值为
1 1 2
三、填空题:本题共3小题,每小题5分,共15分。
槡1-x
12函数f(x)= 的定义域为
lgx
13已知曲线C∶x2+(y-m)2=2和C∶y=x+2,C∶y=|x|+2,若 C与 C 恰有一个公共点,
1 2 1
则实数m= ;若C与C恰有两个公共点,则实数m的取值范围是
2
14已知△ABC的角A,B,C满足tanAtanBtanC≤[tanA]+[tanB]+[tanC],其中符号[x]表示
不大于x的最大整数,若A≤B≤C,则tanC-tanB=
四、解答题:本题共5个小题,共77分。解答应写出说明文字、证明过程或演算步骤。
15(13分)
x2 y2
已知双曲线E∶ - =1(a>0,b>0)的左顶点是A(-1,0),一条渐近线的方程为y=x
a2 b2
(1)求双曲线E的离心率;
1 1
(2)设直线y= x- 与双曲线E交于点P,Q,求线段PQ的长
2 2
蚌埠市高三年级数学试卷第2页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}16(15分)
寒假期间小明每天坚持在“跑步3000米”和“跳绳2000个”中选择一项进行锻炼,在不下
雪的时候,他跑步的概率为60%,跳绳的概率为40%,在下雪天,他跑步的概率为20%,跳
绳的概率为80%若前一天不下雪,则第二天下雪的概率为50%,若前一天下雪,则第二
天仍下雪的概率为40%已知寒假第一天不下雪,跑步3000米大约消耗能量330卡路里,
跳绳2000个大约消耗能量220卡路里记寒假第n天不下雪的概率为p
n
{ 6}
(1)求p,p,p的值,并证明 p- 是等比数列;
1 2 3 n 11
(2)求小明寒假第n天通过运动锻炼消耗能量的期望
17(15分)
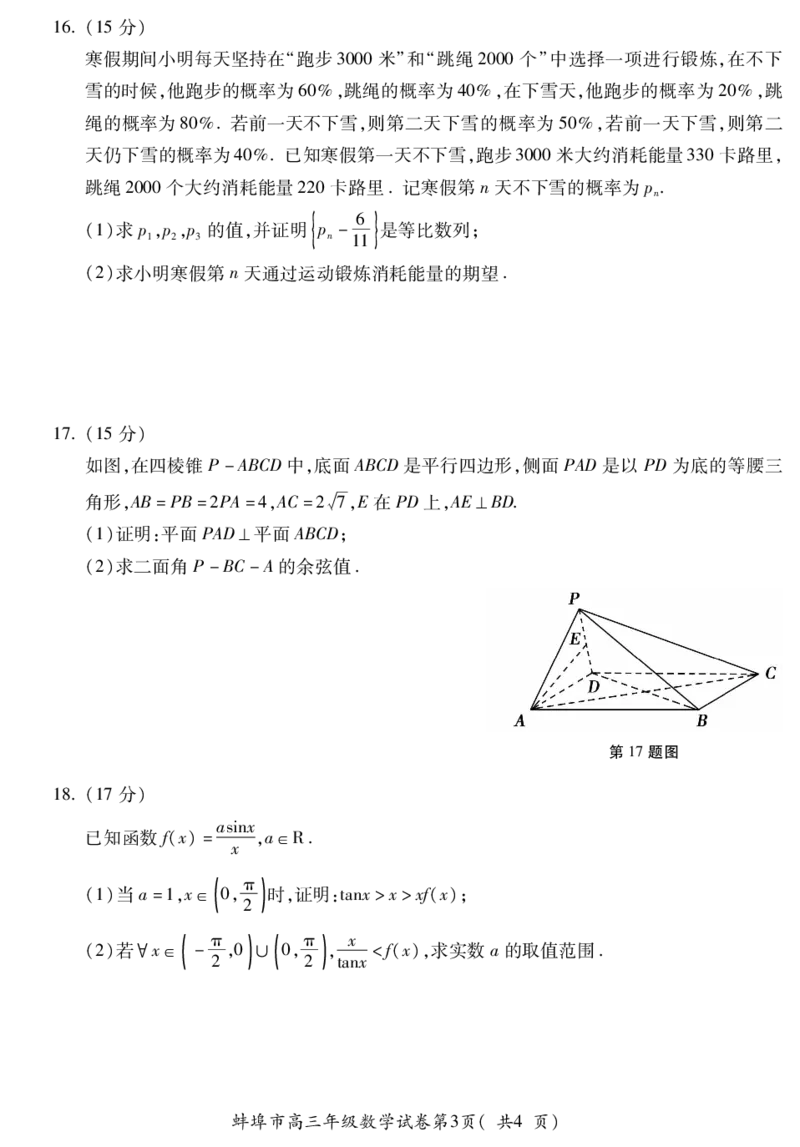
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面 PAD是以 PD为底的等腰三
角形,AB=PB=2PA=4,AC=2槡7,E在PD上,AE⊥BD
(1)证明:平面PAD⊥平面ABCD;
(2)求二面角P-BC-A的余弦值
第17题图
18(17分)
asinx
已知函数f(x)= ,a∈R
x
( π)
(1)当a=1,x∈ 0, 时,证明:tanx>x>xf(x);
2
( π ) ( π) x
(2)若x∈ - ,0∪ 0, , <f(x),求实数a的取值范围
2 2 tanx
蚌埠市高三年级数学试卷第3页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}19(17分)
∞ a a a
对于无穷数列a,a,a,…,a,…,我们称f(x)=∑ nxn=a+ax+ 2x2+…+ nxn+…
0 1 2 n n=0n! 0 1 2! n!
(规定0!=1)为无穷数列{a}的指数型母函数无穷数列1,1,…,1,…的指数型母函数
n
∞ 1 x2 xn
记为e(x)=∑ xn=1+x+ +…+ +…,它具有性质e(x)e(y)=e(x+y)
n=0n! 2! n!
1
(1)证明:e(-x)= ;
e(x)
∞ (-1)k x2 x4 x2k
(2)记c(x)=∑ x2k=1- + +…+(-1)k +…
k=0(2k)! 2! 4! (2k)!
e(ix)+e(-ix)
证明:c(x)= (其中i为虚数单位);
2
x x ∞ B B
(3)以函数 为指数型母函数生成数列{B}, =∑ nxn=B +Bx+ 2x2+
e(x)-1 n e(x)-1 n=0n! 0 1 2!
B
…+ nxn+…其中B 称为伯努利数
n! n
1
证明:B=- 且B =0(k=1,2,3,…)
1 2 2k+1
蚌埠市高三年级数学试卷第4页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}