文档内容
高一数学试卷
一、单选题
a
1.在锐角△ABC中,A,B,C的对边分别是a,b,c,若c=b(1+2cosA),则 的取值范围是
b
( )
(1 √3)
A.(1,√3) B.(√2,√3) C.(√2,2) D. ,
2 2
2.已知集合A⊆U,B⊆U,且A∩∁ B=∅,则下列说法一定正确的是( )
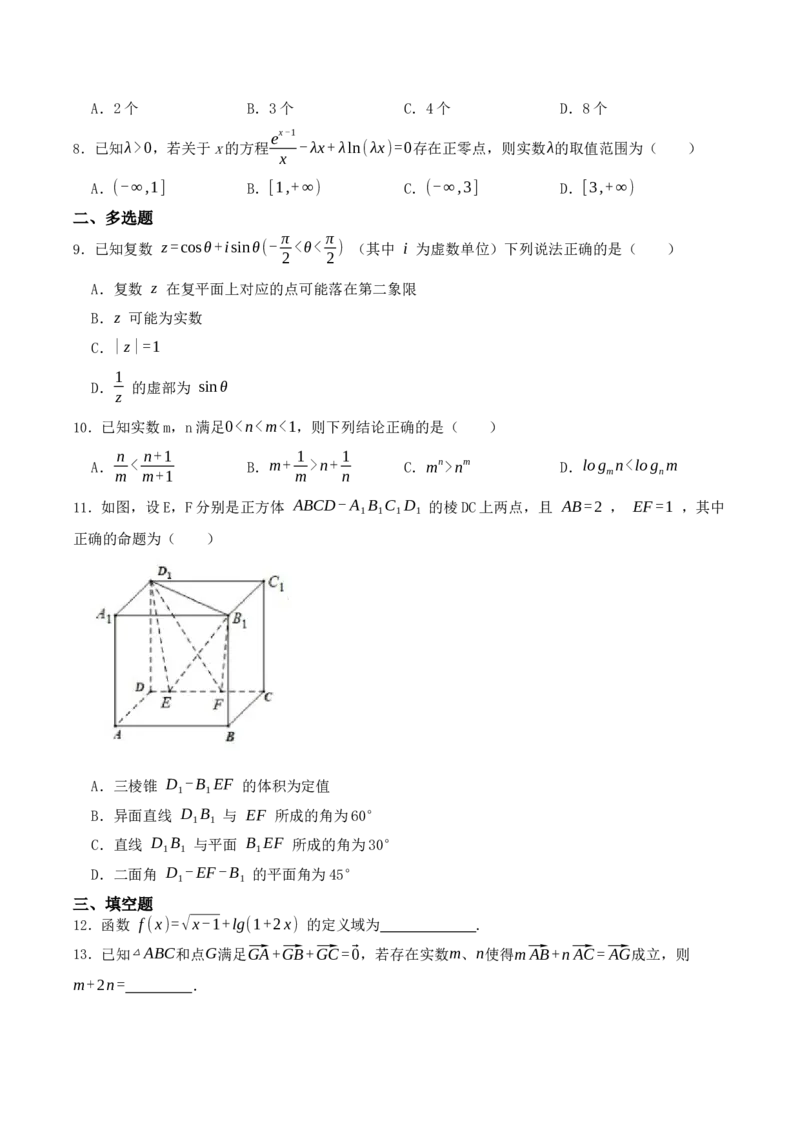
U
A.A⊇B B.A∩B=∅ C.B∩∁ A=∅ D.C A⊇C B
U U U
3.已知集合A={x∈N|(x+1)(2x-7)≤0},B={x|x≤2},则A∩B为( )
A.{-1,0,1,0} B.{-1,0} C.{0,1,2} D.{-1,0,1,2}
4.“Δ=b2-4ac<0”是“关于x的一元二次不等式ax2+bx+c>0的解集为R”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知函数f(x)=|lnx|,x 、x 为不相等的两个实数,则“f (x )=f (x )”是“f' (x )f' (x )=-1”
1 2 1 2 1 2
的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
6.已知定义在R上的函数f (x)满足f (x+2)=f (-x)=-f (x),当0f (a),则实数a的取值范围是( )
( 5 3 )
A. - +4k,- +4k ,k∈Z B.(-1+4k,4k),k∈Z
2 2
( 1 1 ) ( 3 1 )
C. - +4k, +4k ,k∈Z D. - +4k, +4k ,k∈Z
2 2 2 2
7.已知集合A={x∈N|x<4},B={x|x=n2-1,n∈A},P=A∩B,则集合P的子集共有
( )A.2个 B.3个 C.4个 D.8个
ex-1
8.已知λ>0,若关于x的方程 -λx+λln(λx)=0存在正零点,则实数λ的取值范围为( )
x
A.(-∞,1] B.[1,+∞) C.(-∞,3] D.[3,+∞)
二、多选题
π π
9.已知复数 z=cosθ+isinθ(- <θ< ) (其中 i 为虚数单位)下列说法正确的是( )
2 2
A.复数 z 在复平面上对应的点可能落在第二象限
B.z 可能为实数
C.|z|=1
1
D. 的虚部为 sinθ
z
10.已知实数m,n满足0n+ C.mn>nm D.log n,ω>0,|φ|< )的一段图象如图所示.
2
(1)求函数y=f(x)的解析式;
π
(2)将函数y=f(x)的图象向右平移 个单位,得到y=g(x)的图象,求函数y=f(x)+g(x)在
3π
x∈(0, )的值域.
2
a c
18.在△ABC中,角A、B、C的对边分别为a、b、c,若b=2,且cosC= - .
2 4
(1)求角B的大小;
(2)若△ABC是锐角三角形,求△ABC面积的取值范围.
19.已知实数 a,b,c 满足 a>b>c ;
1 1 1
(1)求证: + + >0 ;
a-b b-c c-a
1
(2)将上述不等式加以推广,把 的分子 1 改为另一个大于 1 的自然数 p ,使得
c-a
1 1 p
+ + >0 对任意的 a,b,c 恒成立,请加以证明;
a-b b-c c-a
m n p
(3)从另一角度推广,自然数 m,n,p 满足什么条件时,不等式 + + >0 对任
a-b b-c c-a
意 a,b,c 恒成立,请加以证明.答案解析部分
1.【答案】B
【解析】解:c=b(1+2cosA),由正弦定理可得sinC=sinB(1+2cosA),
则sinAcosB+cosAsinB=sinB+2cosAsinB,即sin(A-B)=sinB,
即A-B=B,即A=2B,若A-B+B=π,则A=π,不符合题意舍去;
a sinA 2sinBcosB
则 = = =2cosB,
b sinB sinB
( π) π
因为A+B+C=3B+C=π,C∈ 0, ,所以3B> ,
2 2
π π π
又因为A=2B< ,所以 0的解集为∅,即充分
性不成立;
{ a>0
必要性:若一元二次不等式ax2+bx+c>0的解集为R,则 ,即必要性成立.
Δ=b2-4ac<0
因此,“b2-4ac<0”是“一元二次不等式ax2+bx+c>0的解集为R”的必要非充分条件.
故选:B.
5.【答案】C
【解析】解:由题意,不妨设01时,f(x)=lnx,f' (x)= ,即f' (x )= ,
x 2 x
21
则f' (x )f' (x )=- =-1,
1 2 x x
1 2
-1 1
当f' (x )f' (x )= ⋅ =-1时,一定有00,函数h(t)单调递增,
又由h(1)=0,所以h(t)存在唯一零点t=1,即1=x-ln(λx)在(0,+∞)有解,
1 x-1
即1+lnλ=x-lnx,令p(x)=x-lnx,则p' (x)=1- = ,
x x
当x∈(0,1)时,p' (x)<0;当x∈(1,+∞)时,p' (x)>0,
所以函数p(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
所以1+lnλ≥p(1)=1,解得λ≥1,
故实数λ的取值范围为[1,+∞).
故答案为:B.
9.【答案】B,Cπ
【解析】对于AB选项,当 - <θ<0 时, cosθ>0 , sinθ<0 ,此时复数 z 在复平面内的点在第
2
四象限;
当 θ=0 时, z=-1∈R ;
π
当 0<θ< 时, cosθ>0 , sinθ>0 ,此时复数 z 在复平面内的点在第一象限.
2
A选项错误,B选项正确;
对于C选项, |z|=√cos2θ+sin2θ=1 ,C选项正确;
1 1 cosθ-isinθ
对于D选项, = = =cosθ-isinθ ,
z cosθ+isinθ (cosθ+isinθ)⋅(cosθ-isinθ)
1
所以,复数 的虚部为 -sinθ ,D选项错误.
z
故答案为:BC.
10.【答案】A,C
n n+1 n-m n n+1
【解析】由00,1- <0,所以m+ -(n+ )=(m-n)(1- )<0,即m+ mm,
由幂函数y=xm 为单调增函数知mm>nm ,故mn>nm,C符合题意;
根据, 0log m=1=log n>log m,D不符合题意,
m m n n
故答案为:AC
11.【答案】A,C,D
【解析】如图所示,1 1 1 2
对A,三棱锥 D -B EF 的体积为 V = S ·B C = × ×2×2×1= 为定值,A符合题意;
1 1 3 △D 1 EF 1 1 3 2 3
对B, EF//D C , ∠B D C 或其补角是异面直线 D B 与 EF 所成的角,为 45° ,B不符
1 1 1 1 1 1 1
合题意;
对C,取 A D 的中点 O ,连结 D O,B O ,则 D O⊥ 平面 B EF ,
1 1 1 1 1
D O √2 1
∠D B O 为直线 D B 与平面 B EF 所成的角,所以 sin∠D B O= 1 = = ,
1 1 1 1 1 1 1 D B 2√2 2
1 1
所以直线 D B 与平面 B EF 所成的角为30°,C符合题意;
1 1 1
对D, A D , D D 均与交线 EF 垂直,所以二面角 D -EF-B 的平面角为 ∠A DD =45∘ ,
1 1 1 1 1 1
,D符合题意.
故答案为:ACD
12.【答案】[1,+∞)
{x-1≥0
【解析】由题意可知, ,解得 x≥1 ,所以 f(x) 的定义域为[1,+∞).
1+2x>0
故答案为:[1,+∞)
13.【答案】1
【解析】因为⃗GA+⃗GB+⃗GC=0⃗,
所以-⃗AG+⃗AB-⃗AG+⃗AC-⃗AG=0⃗,
即-3⃗AG+⃗AB+⃗AC=0⃗,
1 1
所以 ⃗AB+ ⃗AC=⃗AG,
3 31
则m=n= ,所以m+2n=1。
3
故答案为:1。
1
14.【答案】
8
a2+b2+1+2ab (a+b) 2+1 1
【解析】2sinC= = =a+b+ ⩾2 ,
a+b a+b a+b
1
所以 sinC⩾1 ,当且仅当 a+b= ,即 a+b=1 时取等号,
a+b
π
所以 sinC=1 ,即 C= , a+b=1 ,
2
所以 1=(a+b) 2=a2+b2+2ab⩾4ab ,当且仅当 a=b 时取等号,
1
所以 ab⩽ ,
4
1 1 1
则 ΔABC 面积 S= ab⩽ ,即面积的最大值 .
2 8 8
1
故答案为: .
8
⃗a⋅⃗b 6 1
15.【答案】(1)解:因为|⃗a|=4,|⃗b|=3,⃗a⋅⃗b=6,所以cos⟨⃗a,⃗b⟩= = = ,且
|⃗a||⃗b| 4×3 2
π
⟨⃗a.⃗b⟩∈[0,π],所以 ⟨⃗a.⃗b⟩= ,
3
π
则⃗a与⃗b的夹角为 ;
3
(2)解:|3⃗a-4⃗b|=√9⃗a2+16⃗b2-24⃗a⋅⃗b=√144+144-24×6=12.
【解析】(1)代入向量的夹角公式求解即可;
(2)根据向量数量积的运算律和夹角公式求解即可.
⃗a⋅⃗b 6 1
(1)cos⟨⃗a,⃗b⟩= = = ,且⟨⃗a.⃗b⟩∈[0,π],
|⃗a||⃗b| 4×3 2
π π
所以 ⟨⃗a.⃗b⟩= ,所以⃗a与⃗b的夹角为 ;
3 3(2)|3⃗a-4⃗b|=√9⃗a2+16⃗b2-24⃗a⋅⃗b=√144+144-24×6=12.
27 - 2 49 0.5 - 2 2
16.【答案】(1)解:原式=( ) 3-( ) +(0.008) 3×
8 9 25
3 -2 7 1 -2 2
=( ) - +( ) ×
2 3 5 25
4 7 2 4 7 1
= - +25× = - +2= ;
9 3 25 9 3 9
1
(2)解:原式 =log 33+log 2× -2+lg10
3 3 log 2
3
=3+1-2+1=3.
【解析】(1)利用指数幂的运算法则,从而化简求值。
(2)利用换底公式结合对数的运算法则,进而化简求值。
11π π 2π
17.【答案】(1)解:观察图象,得A=2,函数f(x)的周期T= -(- )=π= ,解得ω=2,
12 12 ω
即f(x)=2sin(2x+φ),
π π π π π π
由f(- )=2sin(- +φ)=0,得- +φ=kπ,即φ=kπ+ ,k∈Z,而|φ|< ,则φ= ,
12 6 6 6 2 6
π
所以函数y=f(x)的解析式是f(x)=2sin(2x+ ).
6
π π π
(2)解:由(1)得g(x)=2sin[2(x- )+ ]=2sin(2x- )=-2cos2x,
3 6 2
π √3 1
则y=f(x)+g(x)=2sin(2x+ )-2cos2x=2( sin2x+ cos2x)-2cos2x
6 2 2
π π π π 5π
=√3sin2x-cos2x=2sin(2x- ),当0b>c ,
1 1 1 1 1 1 1
要证 + + >0 ,即证 + > = ,
a-b b-c c-a a-b b-c a-c (a-b)+(b-c)1 1
只要证 ( + )[(a-b)+(b-c)]>1 ,
a-b b-c
1 1 a-b b-c √a-b b-c a-b b-c
而 ( + )[(a-b)+(b-c)]=2+ + ≥2+2 × =4 ,当且仅当 =
a-b b-c b-c a-b b-c a-b b-c a-b
.即 a-b=b-c 或 a+c=2b 时等号成立,
所以原不等式成立
1 1
(2)解:由(1) p<( + )[(a-b)+(b-c)] 恒成立,由(1)
a-b b-c
1 1
( + )[(a-b)+(b-c)] 最小值为4,所以 p<4 , 10 恒成立,即 p<( + )[(a-b)+(b-c)] ,
a-b b-c c-a a-b b-c
m n m(b-c) n(a-b)
而 ( + )[(a-b)+(b-c)]=m+n+ + ≥m+n+2√mn ,当且仅当
a-b b-c a-b b-c
m(b-c) n(a-b)
= ,即 √m(b-c)=√n(a-b) 时等号成立,
a-b b-c
所以 p0 对任意 a,b,c
a-b b-c c-a
恒成立
1 1
【解析】(1)不等式变形为证明 ( + )[(a-b)+(b-c)]>1 ,由基本不等式易证;(2)不
a-b b-c
1 1 1 1
等式变形为 p<( + )[(a-b)+(b-c)] ,由(1)可得 ( + )[(a-b)+(b-c)] 最小
a-b b-c a-b b-c
m n
值.即得 p 的范围.(3)类似(1)得 p<( + )[(a-b)+(b-c)] ,由基本不等式求得
a-b b-c
m n
( + )[(a-b)+(b-c)] 的最小值,从而可得结论.
a-b b-c