文档内容
A级:“四基”巩固训练
一、选择题
1.已知函数f(x)=(x∈[2,6]),则函数的最大值为( )
A.0.4 B.1 C.2 D.2.5
答案 C
解析 ∵函数f(x)=在[2,6]上单调递减,∴f(x) =f(2)==2.
max
2.函数f(x)=则f(x)的最大值、最小值分别为( )
A.10,6 B.10,8
C.8,6 D.以上都不对
答案 A
解析 当1≤x≤2时,8≤2x+6≤10,当-1≤x<1时,6≤x+7<8.∴f(x) =
min
f(-1)=6,f(x) =f(2)=10.故选A.
max
3.已知函数y=x2-2x+3在区间[0,m]上有最大值3,最小值2,则m的取
值范围是( )
A.[1,+∞) B.[0,2]
C.(-∞,2] D.[1,2]
答案 D
解析 由y=x2-2x+3=(x-1)2+2知,当x=1时,y的最小值为2,当y=3
时,x2-2x+3=3,解得x=0或x=2.由y=x2-2x+3的图象知,当m∈[1,2]时,
能保证y的最大值为3,最小值为2.
4.当0≤x≤2时,a<-x2+2x恒成立,则实数a的取值范围是( )
A.(-∞,1] B.(-∞,0]
C.(-∞,0) D.(0,+∞)
答案 C
解析 令 f(x)=-x2+2x,则 f(x)=-x2+2x=-(x-1)2+1.又∵x∈[0,2],
∴f(x) =f(0)=f(2)=0.∴a<0.
min
5.已知函数f(x)=-x2+4x+a,x∈[0,1],若f(x)有最小值-2,则f(x)的最大
值为( )
A.-1 B.0 C.1 D.2
答案 C
解析 因为f(x)=-(x2-4x+4)+a+4=-(x-2)2+4+a,所以函数f(x)图象
的对称轴为x=2.又因为函数图象开口向下,所以f(x)在[0,1]上单调递增.又因为
f(x) =-2,所以f(0)=-2,即a=-2.所以f(x) =f(1)=-1+4-2=1.
min max
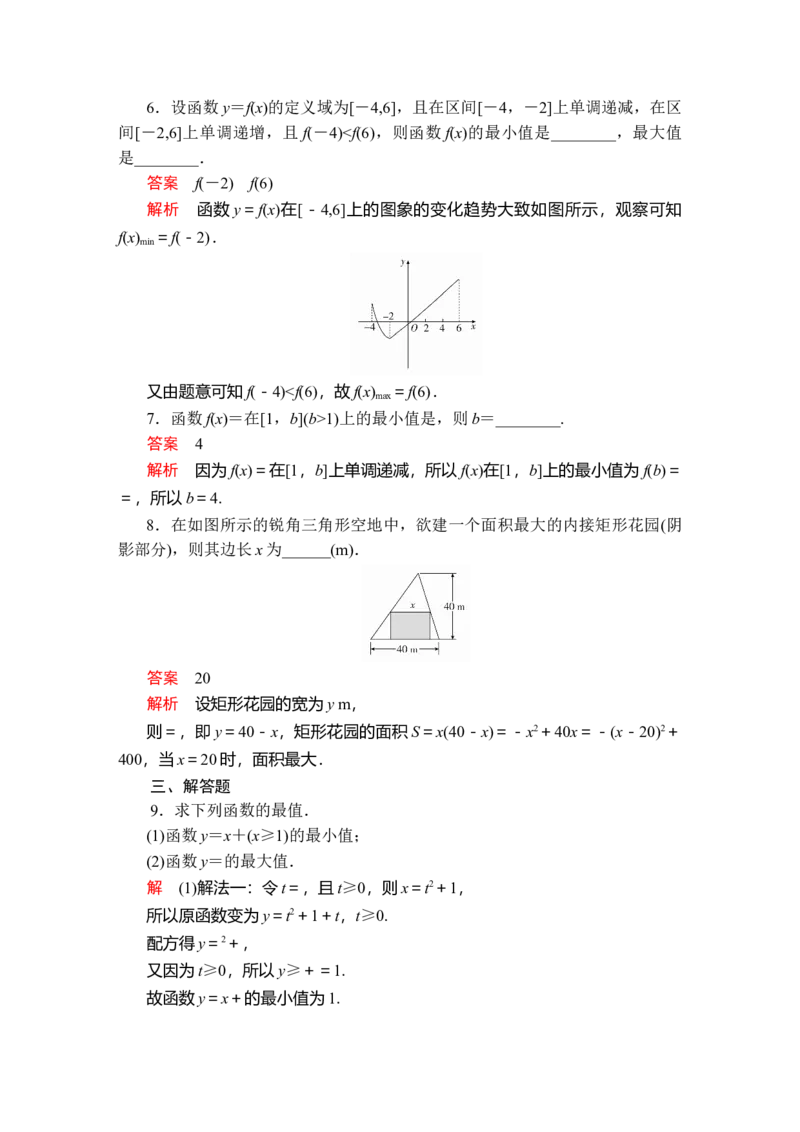
二、填空题6.设函数y=f(x)的定义域为[-4,6],且在区间[-4,-2]上单调递减,在区
间[-2,6]上单调递增,且f(-4)1)上的最小值是,则b=________.
答案 4
解析 因为f(x)=在[1,b]上单调递减,所以f(x)在[1,b]上的最小值为f(b)=
=,所以b=4.
8.在如图所示的锐角三角形空地中,欲建一个面积最大的内接矩形花园(阴
影部分),则其边长x为______(m).
答案 20
解析 设矩形花园的宽为y m,
则=,即y=40-x,矩形花园的面积S=x(40-x)=-x2+40x=-(x-20)2+
400,当x=20时,面积最大.
三、解答题
9.求下列函数的最值.
(1)函数y=x+(x≥1)的最小值;
(2)函数y=的最大值.
解 (1)解法一:令t=,且t≥0,则x=t2+1,
所以原函数变为y=t2+1+t,t≥0.
配方得y=2+,
又因为t≥0,所以y≥+=1.
故函数y=x+的最小值为1.解法二:因为函数y=x和y=(x≥1)均为增函数,故函数y=x+(x≥1)为增函
数,所以当x=1时y取得最小值,即y =1.
min
(2)y===2+=2+.
因为2+≥,
所以2<2+≤2+=.
故函数的最大值为.
10.已知函数 f(x)=ax+(1-x)(a>0),且 f(x)在[0,1]上的最小值为 g(a),求
g(a)的最大值.
解 f(x)=x+,
当a>1时,a->0,此时f(x)在[0,1]上单调递增,
∴g(a)=f(0)=;
当00 时,
f(x)<0,f(1)=-.
(1)求证:f(x)在R上单调递减;
(2)求f(x)在[-3,3]上的最小值.
解 (1)证明:∀x ,x ∈R,且x 0,
2 1
因为x>0时,f(x)<0,
所以f(x -x )<0.
2 1
又因为x =(x -x )+x ,
2 2 1 1
所以f(x )=f[(x -x )+x ]=f(x -x )+f(x ),
2 2 1 1 2 1 1
所以f(x )-f(x )=f(x -x )<0,
2 1 2 1
所以f(x )x >0,则f(x )-f(x )=×0.2-×0.2
1 2 1 2
=×0.2(x -x )-×0.2
1 2
=×0.2
=×0.2(x -x ),
1 2
因为x >x >0,
1 2
所以×0.2(x -x )>0,
1 2
故生产每件产品所需可变资金函数f(x)=×0.2为单调递增函数.
(2)设利润为L(x)万元,则L(x)=R(x)-20-0.2(x2-1)=160x-3.8x2-1480.2
-20-0.2(x2-1)=160x-4x2-1500=-4(x-20)2+100,所以当生产 20万件产
品时利润最大,最大利润为100万元.