第二章直线和圆的方程（A卷·知识通关练）（解析版）_E015高中全科试卷_数学试题_选修1_01.单元测试_单元测试AB卷

班级 姓名 学号 分数 第二章 直线和圆的方程（A卷·知识通关练） 核心知识1 直线的倾斜角与斜率 1．（2022·天津天津·高二期末）若直线l经过A(2，1)，B(1，m2)两点，则l的斜率取值范围为 _________________；其倾斜角的取值范围为_________________.    【答案】 (,1]   0, 4   [ 2 ,) 【解析】因为直线l经过A(2，1)，B(1， m2)两点， 1m2 所以l的斜率为k  1m2 1， 21 (,1] 所以l的斜率取值范围为 ， 设其倾斜角为，[0,)，则tan1，    所以其倾斜角的取值范围为 0,  [ ,)，  4 2    故答案为： (,1] ，  0, 4   [ 2 ,) aR A(a,2) B(a1,3) 2．（2022·上海市控江中学高二期中）设 ，若直线l经过点 ､ ，则直线l的斜率是 ___________. 【答案】1 A(a,2) B(a1,3) 【解析】因为直线l经过点 ､ ， 32 k  1 所以直线l的斜率是 ， a1a 故答案为：1 2x3y10 x5y100 3．（2022·上海虹口·高二期末）直线 与 的夹角为________．  【答案】 4 2 2 【解析】直线2x3y10的斜率 k 1 = 3 ，即倾斜角  满足 tan 3 ，1 1 k  tan 直线 x5y100 的斜率 2 5 ，即倾斜角满足 5 ， 1 2   tan tantan  5 3 1 所以 1tantan  1 2 ， 1   5 3 3   所以 ， 4   又两直线夹角的范围为 0, ，  2  所以两直线夹角为 ， 4  故答案为： . 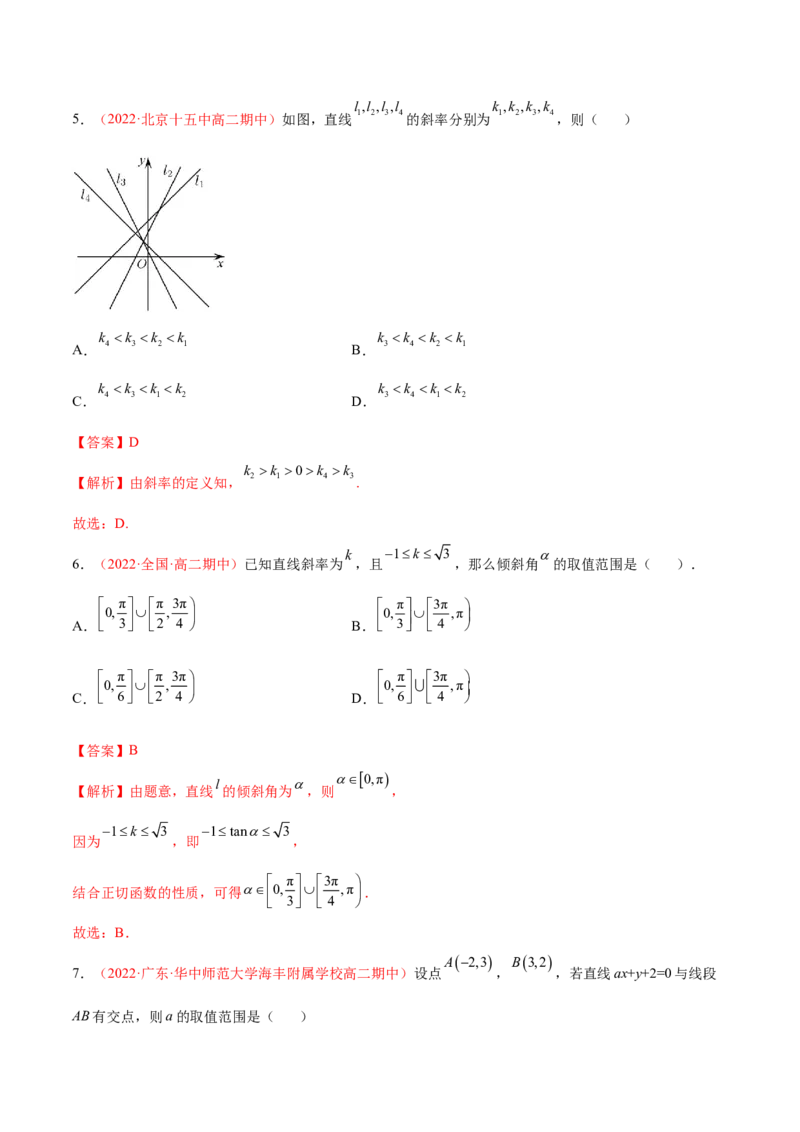4 P0，1 A1，2，B3，2 l l 4．（2022·重庆·高二期末）经过点 作直线 ，直线 与连接 两点的线段总有公共点， 则直线l的斜率k的取值范围是________．  1 【答案】 3，   3 21 21 1 k  3 k   【解析】 ， ，而 ， PA 10 PB 30 3 013 1 3k  因此 ， 3  1 故答案为： 3, ．  3l,l ,l ,l k ,k ,k ,k 5．（2022·北京十五中高二期中）如图，直线 1 2 3 4的斜率分别为 1 2 3 4，则（ ） k k k k k k k k A． 4 3 2 1 B． 3 4 2 1 k k k k k k k k C． 4 3 1 2 D． 3 4 1 2 【答案】D k k 0k k 【解析】由斜率的定义知， 2 1 4 3. 故选：D. 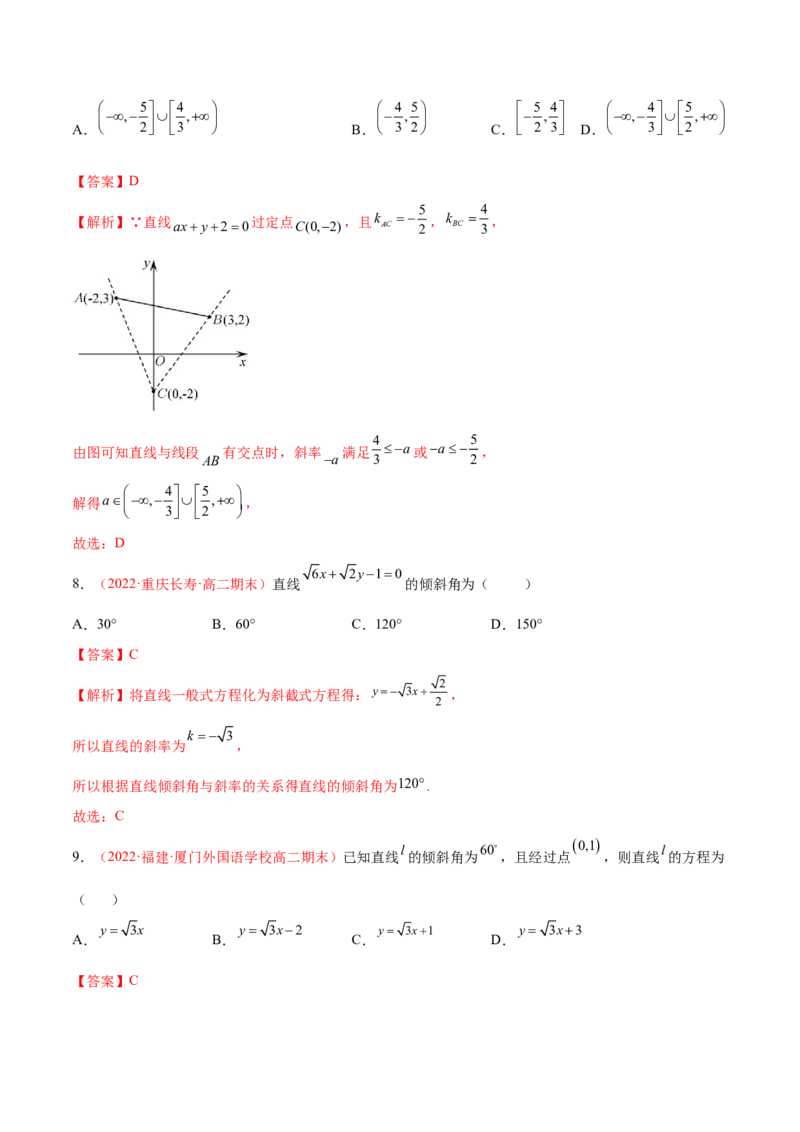k 1k  3  6．（2022·全国·高二期中）已知直线斜率为 ，且 ，那么倾斜角 的取值范围是（ ）．  π π 3π  π 3π   0,    ,   0,    ,π A． 3 2 4  B． 3  4   π π 3π  π 3π   0,    ,   0,  ,π C． 6 2 4  D． 6  4  【答案】B 0,π l  【解析】由题意，直线 的倾斜角为 ，则 ， 1k  3 1tan 3 因为 ，即 ，  π 3π  结合正切函数的性质，可得  0,    ,π．  3  4  故选：B． A2,3 B3,2 7．（2022·广东·华中师范大学海丰附属学校高二期中）设点 ， ，若直线ax+y+2=0与线段 AB有交点，则a的取值范围是（ ） 5 4   4 5  5 4  4 5  ,    ,  ,    ,  ,    , A． 2 3  B． 3 2 C． 2 3 D． 3 2  【答案】D 5 4 【解析】∵直线 过定点 ，且k  ，k  ， axy20 C(0,2) AC 2 BC 3 4 5 由图可知直线与线段 有交点时，斜率 满足 a或a ， AB a 3 2  4 5  解得a,    ,，  3 2  故选：D 6x 2y10 8．（2022·重庆长寿·高二期末）直线 的倾斜角为（ ） A．30° B．60° C．120° D．150° 【答案】C 2 【解析】将直线一般式方程化为斜截式方程得：y 3x ， 2 k  3 所以直线的斜率为 ， 所以根据直线倾斜角与斜率的关系得直线的倾斜角为120. 故选：C 0,1 l 60 l 9．（2022·福建·厦门外国语学校高二期末）已知直线 的倾斜角为 ，且经过点 ，则直线 的方程为 （ ） y 3x y 3x2 y 3x1 y 3x3 A． B． C． D． 【答案】Cl 3 l y 3x1 【解析】由题意知：直线 的斜率为 ，则直线 的方程为 . 故选：C. 核心知识2 直线方程的五种形式 A1,2 B1,2 l l 10．（2022·全国·高二期末）直线 过点 、 ，则直线 的方程为______． 【答案】2xy0 22 【解析】由题设，k  2，则直线 的方程为 ，整理得 . AB 1(1) l y22(x1) 2xy0 故答案为：2xy0 1,2 l 11．（2022·江西·南昌市第八中学高二期中（理））直线 过点 ，且在两坐标轴上截距相等，则直线 l的一般式方程为___________. 【答案】xy10，2xy0 y2kx1 l 0 l 【解析】显然直线 的斜率存在且不为 ，设 ： 2k x 令 x0 ，则y2k ；令 y0 ，则 k 2k 依题意， 2k k 解之得k 1或k 2 当k 1时，l：xy10 当k 2时，l：2xy0 故答案为：xy10，2xy0 12．（2022·浙江省诸暨市第二高级中学高二期中）已知直线axy2a0在两坐标轴上的截距相等，则 实数a（ ） A．1 B．1 C．2或1 D．2或1 【答案】D 【解析】当a0时，直线y2，此时不符合题意，应舍去； 当a2时，直线l:2xy0，在x轴与 y 轴上的截距均为0，符合题意； 2a 当 a0 且 a2 ，由直线l:axy2a0可得：横截距为 a ，纵截距为 2a .2a 由 2a，解得： . a a1 故a的值是2或1. 故选：D A2,1 l l 13．（2022·全国·高二期中）已知直线 过 ，并与两坐标轴截得等腰三角形，那么直线 的方程是 （ ）． xy10 xy30 xy10 x y30 A． 或 B． 或 xy10 x y30 xy10 xy30 C． 或 D． 或 【答案】C 【解析】由题意可知，所求直线的倾斜角为45或135，即直线的斜率为1或-1， 故直线方程为y1 x2或y1(x2)， x y30 xy10 即 或 . 故选：C. 14．（2022·上海市大同中学高二期中）如果AB>0且BC<0，那么直线Ax＋By＋C＝0不经过第（ ）象 限 A．一 B．二 C．三 D．四 【答案】C A AB C BC 【解析】因AB>0且BC<0，则直线Ax＋By＋C＝0的斜率k   0，纵截距b  0， B B2 B B2 所以直线Ax＋By＋C＝0必过第一、二、四象限，不经过第三象限. 故选：C 15．（2022·天津天津·高二期末）经过点A(0，－3)且斜率为2的直线方程为（ ） 2xy30 2xy30 x2y60 x2y60 A． B． C． D． 【答案】A 【解析】因为直线经过点A(0,3)且斜率为2， 所以直线的方程为y32(x0)， 即2xy30， 故选：A．16．（2022·天津市红桥区教师发展中心高二期中（文））完成下面问题： (1)求直线2x5y200分别在x轴， y 轴上的截距； xy20 2 (2)求平行于直线 ，且与它的距离为 的直线的方程； (3)已知两点M(7,1)，N(5,4)，求线段MN的垂直平分线的方程. x y  1 【解析】(1)将 化为截距式 ，由此可知此直线在x轴、y轴上的截距分别为10与4. 2x5y200 10 4 xy20 xyc0 (2)因为所求直线平行于直线 ，所以可设所求直线方程为 ， c2 d   2 这两条直线间的距离 1212 ，解得c=0或c=4，直线方程为 xy0 或 xy40 ； 4(1) 5 1 12 k   k   (3)直线MN的斜率 MN 57 12，MN的垂直平分线的斜率 k 5 MN  3 MN的中点坐标为1, ，  2 3 12 所以线段MN的垂直平分线的方程为y  (x1)，整理得 . 2 5 24x10y90 17．（2022·吉林长春·高二期中（文））已知 ABC的三个顶点的坐标为 A1,1 ， B3,2 ， C5,4 ． (1)求边AB上过点C的高所在直线的方程； (2)若直线l与AC平行，且在x轴上的截距比在y轴上的截距大1，求直线l与两条坐标轴围成的三角形的 周长． 1 【解析】(1) k AB  2 ，  边AB上的高所在直线的斜率为 2 ， 又 直线过点C5,4，   y42x5 2xy140 所求直线的方程为： ，即 ； x y a 3 a 3 3 (2)设直线l的方程为： a1  a 1，即y a1 xa， k AC  4 ， a1  4 ，解得：a 7 ， x y  1 4 3 直线l的方程为：  ，  7 7 4   3 4 2 3 2 5  直线l过点 7 ,0  ,  0, 7   ，三角形斜边长为  7    7    7，5 4 3 12 直线l与坐标轴围成的直角三角形的周长为    ．  7 7 7 7 核心知识3 直线的平行与垂直 l :(m1)x6y20,l :mxy10 l l 18．（2022·浙江·长兴县教育研究中心高二期中）已知两直线 1 2 ，若 1 2， 则m____；若l∥l，则m______. 1 2 1 【答案】 3或-2 7 l :m1x6y20 l :mxy10 【解析】因为 1 ， 2 ， 所以，若 l 1 l 2，则 mm160 ，解得 m3 或 2 , 1 m 若l//l ，则 m16m0 ，解得 7 ，经检验适合题意. 1 2 1 故答案为：①3或-2；② 7 mR l mxy10 l 19．（2022·四川·成都七中高二期末（文））已知 ，若直线 1： 与直线 2： 9xmy2m30平行，则m______________． 【答案】3 l mxy10 l 9xmy2m30 【解析】因为直线 1： 与直线 2： 平行， m2910  所以  12m3m1，解得 m3 ， 故答案为：3. 20．（2022·四川南充·高二期末（文））“ m1 ”是“直线 l 1： m4xmy10 与直线 l 2： mxm2y20 互相垂直”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【答案】Al l m(m4)m(m2)0 m0 m1 1 2 【解析】依题意， ，解得 或 ， 所以“ m1 ”是“直线 l 1： m4xmy10 与直线 l 2： mxm2y20 互相垂直”的充分不必要 条件. 故选：A m2 2xm1y40 3xmy20 21．（2022·湖北孝感·高二期末）“ ”是“直线 与直线 垂直”的 （ ） A．充分必要条件 B．充分不必要条件 C．必要不充分条件 D．既不充分也不必要条件 【答案】B 2xm1y40 3xmy20 【解析】直线 与直线 垂直, 23m1m0 m2 m3 则 ，解得： 或 ， m2 2xm1y40 3xmy20 所以“ ”是“直线 与直线 垂直”的充分不必要条件. 故选：B. l :(a1)xay20,l :ax(1a)y10 22．（多选题）（2022·云南普洱·高二期末）已知直线 1 2 ，则 （ ） 2 a A．l 恒过点(2,2) B．若l //l ，则 2 1 1 2 l l a1 0a1 l C．若 1 2，则 D．当 时， 2不经过第三象限 【答案】BD l :(a1)xay20 a(xy)x20 【解析】直线 1 ，则 ， xy0  由x20 ，得x2,y2，所以l 恒过定点(2,2)，所以A错误； 1a1 a 2 2   a 由l //l 可得： a 1a 1，所以 2 ，B正确； 1 2 l l (a1)a(1a)a0 a0 由 1 2可得： ， ，所以C错误； l :ax(1a)y10 a1 l :x1 由 2 ，当 时， 2 ，不过第三象限；  a 0  a1 当 时， ，不过第三象限，只需要 ，解得 ， l :y a x 1  1 0 a1 2 a1 1a 1a 0a1 所以a的取值范围为0a1，所以D正确； 故选：BD. l m4xy10 l 23．（2022·内蒙古·赤峰二中高二期末（文））已知直线 1： 和 2： m4xm1y10 ． l ∥l (1)若 1 2 ，求实数m的值； l l (2)若 1 2，求实数m的值． m4 【解析】(1)由直线l 1 的斜率存在，且为 m4 ，则直线l 2 的斜率也存在，且为 m1 ， l ∥l 1 2 因为 ， m4 m4 所以 ， m1 解得m0或2， 1 1 ①当 m0 时，由 m1 此时直线l 1 ，l 2 重合， 1 1  1 ②当 m2 时， m1 3 ，此时直线l 1 ，l 2 平行， l ∥l 综上：若 1 2，则实数m的值为2． (2)①当 m4 时，直线 l 1的斜率为0，此时若 l 1 l 2必有 m1 ，不可能. m4 1 69 ②当 时，若 必有 m4 1，解得m ， m4 l l  m1 2 1 2 1 69 1 69 由上知若l l ，则实数m的值为 2 或 2 ． 1 2 核心知识4 直线的交点坐标与距离公式 mR l :(m1)xmy2m0 (1,2) 24．（2022·上海市控江中学高二期中）设 ，已知直线 1 ，过点 作直线 l 2，且 l 1 // l 2，则直线 l 1与 l 2之间距离的最大值是___________. 10 【答案】 l :(m1)xmy2m0 mxy1x20 【解析】由直线 1 ，得 ； xy10 x2 令  x20 ，解得  y3 ，则直线l 过定点 2,3 ； 1 又 l 1 //l 2 ，且l 2 过点 1,2 ，则直线l 1 与l 2 之间距离的最大值 d  212 322  10 ； 10 故答案为： . 25．（2022·天津市红桥区教师发展中心高二期中（文））已知点A(1,3)，B(2,6)，若在x轴上存在一点P PA  PB 满足 ，则点P的坐标为___________． 5,0 【答案】 【解析】设 Px,0 ，则 (x1)29  (x2)236 ，解得x5， 5,0  点P的坐标为 ， 5,0 故答案为： ． O0,0 A2,4 B3,6 26．（2022·上海·曹杨二中高二期末）已知三角形OAB顶点 ， ， ，则过B点的中线长为______. 2 17 【答案】 【解析】由中点坐标公式可得OA中点C1,2 ，则过B点的中线长为 BC  132 262 2 17 . 2 17 故答案为： A1,a 4x3y10 27．（2022·重庆长寿·高二期末）在第一象限的点 到直线 的距离为3，则a的值为 __________． 【答案】4 A1,a a0 【解析】 在一象限，所以 ， A1,a 4x3y10 点 到直线 的距离为3，则 43a1 3，解得： 或 . 5 a4 a6 因为a0，所以a4. 故答案为：4. xy20 xy20 28．（2022·贵州遵义·高二期末（文））直线 与直线 的距离为______． 2 2 【答案】 【解析】因为直线xy20与直线xy20平行， 4 4  2 2 所以它们间的距离为： 1212 2 . 2 2 故答案为： l :3x4y60 l :3x4yC 0 29．（2022·广东·江门市第二中学高二期中）直线 1 与 2 间的距离为3，则 C _______. 【答案】9或216C d  3 【解析】由题，可知 l //l ，所以两平行线间距离为 3242 ， 1 2 解得C 9或21， 故答案为：9或21 l :xy10 30．（多选题）（2022·江苏·常州市第一中学高二期中）已知直线 1 ，动直线 l :(k1)xkyk 0(kR) 2 ，则下列结论正确的是（ ） k l k l A．不存在 ，使得 2的倾斜角为90° B．对任意的 ，直线 2恒过定点 k l l k l l C．对任意的 ， 1与 2都不重合 D．对任意的 ， 1与 2都有公共点 【答案】BD k 0 l :x0 【解析】对A，当 时， 2 ，符合倾斜角为90°，故A错误； xy10 x0   对B，l :(k1)xkyk k(xy1)x0，解x0 可得y1，故l 过定点(0,1)，故B正确； 2 2 1 1 1 1 1 对C，当k  2 时，l 2 : 2 x 2 y 2  2 (xy1)0，显然与l :xy10重合，故C错误； 1 l (0,1) (0,1) l :xy10 k l l 对D， 2过定点 ，而 也在 1 上，故对任意的 ， 1与 2都有公共点，故D正确； 故选：BD 1 y x 31．（2022·北京十五中高二期中）过两直线 的交点，且与直线 平行的直线方 xy30,2xy0 3 程为（ ） x3y50 x3y50 A． B． x3y50 x3y50 C． D． 【答案】Cxy30 x1   【解析】由2xy0 解得y2，则直线xy30,2xy0的交点 1,2 ， 1 1 1 又直线y x的斜率为 ，则所求直线方程为y2 x1 ，整理得 . 3 3 3 x3y50 故选：C. 32．（2022·全国·高二期末）已知 P 1 a 1 ,b 1  与 P 2 a 2 ,b 2  是直线 ykx1 （ k 为常数）上两个不同的点，则 axby1 1 1  关于 x 和y的方程组a 2 xb 2 y1的解的情况是（ ） k P P A．无论 ， 1， 2如何，方程组总有解 k P P B．无论 ， 1， 2如何，方程组总有唯一解 k P P C．存在 ， 1， 2，方程组无解 k P P D．存在 ， 1， 2，方程组无穷多解 【答案】B 【解析】已知 P 1 a 1 ,b 1  与 P 2 a 2 ,b 2  是直线 ykx1 （ k 为常数）上两个不同的点， b b k  2 1 所以 a a ,即a a ,并且b ka 1,b ka 1，a b ab  kaa kaa a a a a . 1 2 1 2 1 1 2 2 2 1 1 2 1 2 1 2 2 1 2 1 axby1① 1 1  所以 a xb y1② 2 2 ①b ②b ab a b xb b a a xb b 2 1得： 1 2 2 1 2 1即 1 2 2 1, 所以方程组有唯一解. 故选：B axby10 a xb y10 P(1,2) 33．（2022·安徽省六安中学高二期中（文））已知两直线 1 1 和 2 2 的交点为 ，Q(a,b), Q (a ,b ) 则过 1 1 1 2 2 2 两点的直线方程为（ ） x2y10 x2y10 2xy10 2x y10 A． B． C． D． 【答案】B axby10 a xb y10 P(1,2) 1 1 2 2 【解析】依题意两直线 和 的交点为 ， a 2b 10,a 2b 10，Q,Q x2y10 1 1 2 2 1 2 所以 在直线 上， Q(a,b), Q (a ,b ) x2y10 1 1 1 2 2 2 所以过 两点所在直线方程为 ， 故选：B Px，y xy10 x22y22 34．（2022·湖南·周南中学高二期末）已知点 在直线 上的运动，则 的 最小值是（ ） 2 1 3 1 A．2 B． 2 C．4 D． 4 【答案】A x22y22 Px，y 2,2 【解析】 表示点 与 距离的平方， 1 2 d   因为点 2,2 到直线xy10的距离 2 2 ， 1 所以2,2的最小值为 d2  ． 2 故选：A 2mx12my43m0 l mR l 35．（2022·全国·高二期末）已知直线 ： （ ）．求证：直线 恒过定 点P，并求点P的坐标． 2xy40, x1, 【解析】证明：原方程整理为2xy4mx2y30，则由  x2y30,得  y2. 1,2 P 所以 点坐标为 ．36．（2022·全国·高二期中）直线 l ： 4x3y70 上的一点P到 A1,2 和 B5,8 两点的距离相等，试求 P点坐标． 82 【解析】易得 P 在 AB 的垂直平分线上， AB 的中点坐标为2,5，又k AB  51 1，则 AB 的垂直平分线斜 率为1，  xy70, x2, 则方程为y5(x2)，即xy70，由  4x3y70,解得  y5.所以 P 点坐标为 2,5 ． (41)x(1)y30 37．（2022·江苏·东海县教育局教研室高二期中）已知直线l： . (1)求证：直线l过定点； l x-2y+2=0 l x2y60 (2)若直线l被两平行直线 1： 与 2： 所截得的线段AB的中点恰好在直线 2xy60上，求的值. (41)x(1)y30 (4xy)xy30 【解析】(1)由已知： ，即 ， 4xy0  令xy30，解得：x=1，y=4， ∴直线l恒过定点(1,4). l l 2xy60 (2)设直线 1， 2分别与直线 交于C，D两点， 2xy60  14 2   ,  由x2y20，解得C 5 5， 2xy60  6 18   ,  由x2y60，解得D 5 5 ， ∴CD的中点M的坐标为(－2,－2)， l l 不妨设A在直线 1上，B在直线 2上，则△AMC≌△BMD，即MA=MB，故M(－2,－2)为AB的中点， 1  将M代入直线l的方程得：(41)(2)(1)(2)30，解得 · 2 A3,3 B2,2 C7,1 ABC 38．（2022·全国·高二期中）已知 的三个顶点的坐标为 、 、 ，试求：(1)BC边上的高所在的直线方程； (2) ABC的面积． 21 1 【解析】（1）因为k   ，则 边上的高的斜率为3，又经过A点，故方程为 BC 2(7) 3 BC y33x3 3xy60 ，化简得 ． 1 （2）BC  272(21)2 3 10，直线 BC 方程为y2 3 (x2)，整理得 x3y40 ，则 A 到 3334 16 1 16  3 10 24 BC的距离为 1232 10 ，则 ABC的面积为2 10 .  39．（2022·全国·高二期中）已知直线 l 过点 P2,3 ，且被平行直线 l 1： 3x4y70 与 l 2： 3x4y80 3 2 l 所截取的线段长为 ，求直线 的方程． 8(7) d  3 【解析】两条平行线之间的距离 3242 ，截得的线段长为3 2，推得直线l与l 1 、l 2 的夹角为 45°． 3 k 4 tan45 1 设直线 的斜率为 ，故 3 1 k l k 4 1 解得：k  或 7 k7 1 y3 (x2) 则直线 l 的方程为： 7 或y37(x2). 整理得：x7y190或7x y170. 核心知识5 对称问题 Q1,2 xy10 40．（2022·吉林油田高级中学高二期中）已知点P与点 关于直线 对称，则点P的坐标 为_______.3,0 【答案】 Pm,n 【解析】由题可知该直线是线段PQ的垂直平分线，设 ， m1 n2  10,   2 2 则 n2 解得m3,  1,   m1 n0. 故答案为：(3，0). 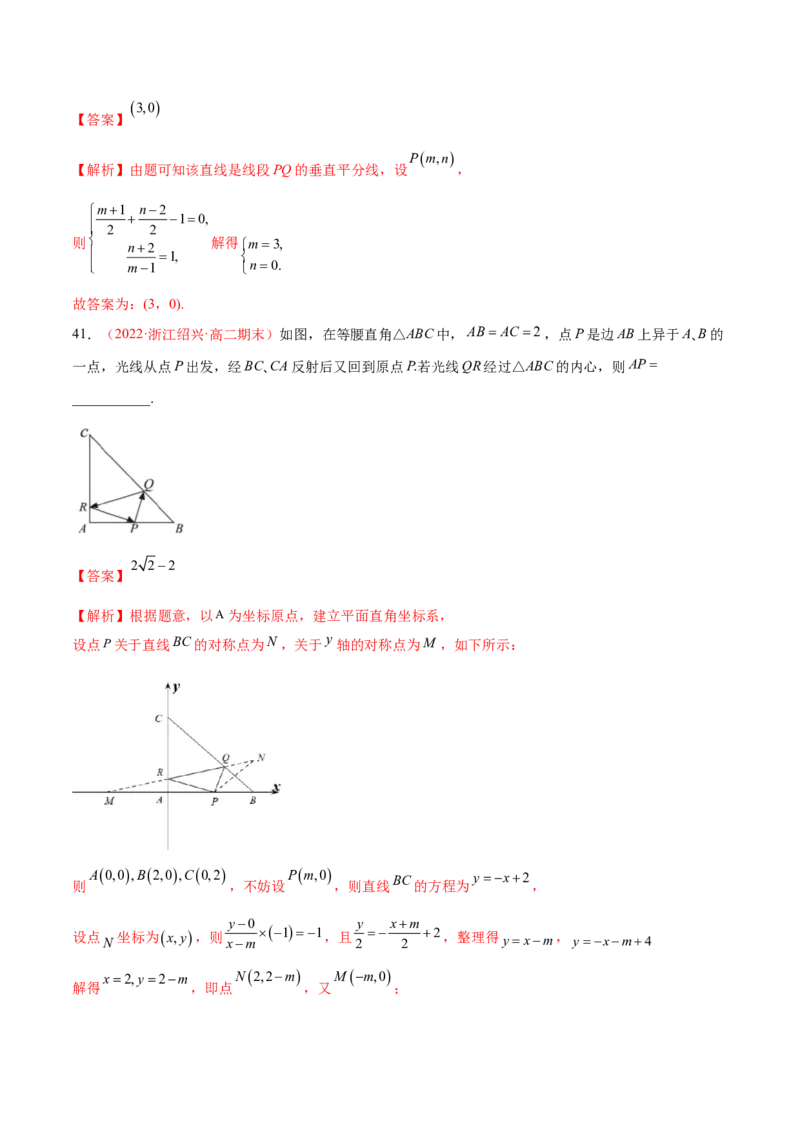41．（2022·浙江绍兴·高二期末）如图，在等腰直角△ABC中，AB AC 2，点P是边AB上异于A､B的 一点，光线从点P出发，经BC､CA反射后又回到原点P.若光线QR经过△ABC的内心，则AP ___________. 2 22 【答案】 【解析】根据题意，以A为坐标原点，建立平面直角坐标系， 设点P关于直线BC的对称点为N ，关于 y 轴的对称点为M ，如下所示： A0,0,B2,0,C0,2 Pm,0 BC yx2 则 ，不妨设 ，则直线 的方程为 ， y0 y xm 设点 N 坐标为x,y，则 xm 11 ，且 2  2 2 ，整理得 yxm ， yxm4 x2,y2m N2,2m Mm,0 解得 ，即点 ，又 ；r  1 设△ 的内切圆圆心为 ，则由等面积法可得 222 2  22，解得 ； ABC r 2 2 r2 2   2 2,2 2 故其内心坐标为 ， 2m 2 2    m22m 21 0 由M,N及△ABC的内心三点共线，即2m 2 2m，整理得 ， m0 2 22 AP2 22 解得 （舍）或 ，故 . 2 22 故答案为： . l :xy30 l:xy10 l 42．（2022·全国·高三专题练习）已知直线 1 ，直线 ，若直线 1关于直线l的对称 l l 直线为 2，则直线 2的方程为_______________． xy50 【答案】 . l//l l :xym0m3,m1 l M0,3 【解析】由题意知 1 2，设直线 2 ，在直线 1上取点 ， M'a,b M l 设点 关于直线 的对称点为 ，  b3 11   a 则 ， 解得 ，即 ， a0 b3   10  2 2 a4,b1 M'4,1 M'4,1 l 41m0,m5 将 代入 2的方程得 ， l xy50 所以直线 2的方程为 . 故答案为：xy50 l :xy30 l:xy10 l 43．（2022·全国·高三专题练习）已知直线 1 ，直线 ，若直线 1关于直线l的对称 l l 直线为 2，则直线 2的方程为_______________． xy50 【答案】 .l//l l :xym0m3,m1 l M0,3 【解析】由题意知 1 2，设直线 2 ，在直线 1上取点 ， M'a,b M l 设点 关于直线 的对称点为 ，  b3 11   a 则 ， 解得 ，即 ， a0 b3   10  2 2 a4,b1 M'4,1 M'4,1 l 41m0,m5 将 代入 2的方程得 ， l xy50 所以直线 2的方程为 . 故答案为：xy50 2x5y30 M(1,2) 44．（2022·全国·高二课时练习）直线 关于点 对称的直线方程是______． 【答案】2x5y130 l:2x5yC 0 0 【解析】设对称直线为 ， 8C 2523 0  则有 2252 2252 ， C 3 C 13 解这个方程得 0 （舍）或 0 . 所以对称直线l的方程中2x5y130 故答案为：2x5y130 l:xy10 l :xy30 l :2xy10 1 2 45．（2022·全国·高二课时练习）已知直线 ， ， ． l l l （1）求直线 1关于直线 的对称直线 1 的方程； （2）求直线 l 2关于直线 l 的对称直线 l 2  的方程． l //l l//l 【解析】（1）因为 1 ，所以 1 ． l xyc0 c3 c1 设直线 1 的方程为 （ ，且 ）．在直线 l 1上取点 M0,3 ，设点 M 关于直线 l 的对称点为 Ma,b ， b3 11   a 则 a0 b3 ，解得a4 ，   10   2 2 b1 M 4,1 即点 的坐标为 ． 把点 M 的坐标代入直线 l 1  的方程，得 41c0 ，解得 c5 ， l xy50 所以直线 1 的方程为 ． 2xy10 x0   （2）由xy10 ，得y1， l A0,1 所以 2与l的交点坐标为 ． l B1,1 另取 2上不同于A的一点 ， B1,1 Bm,n l 设 关于 的对称点为 ， m1 n1  10   2 2 则 n1 ，得m2，  1  m1 n0 2,0 B 即点 的坐标为 ． 10 所以过A0,1与B2,0的直线 l 的方程为y 02 x2 ， 2 即x2y20． 46．（2022·江苏·高二课时练习）已知直线l:y3x3，求： M(3,2) (1)直线l关于点 对称的直线的方程； xy20 (2)直线 关于直线l对称的直线的方程． l M(3,2) A(x,y) 【解析】(1)设直线 关于 的对称直线上任意一点为 ，M(3,2) B(x,y ) 则点 A 关于点 的对称为 1 1 ， xx 1 3   2 则 ，解得 ，即 , yy  1 2  2 x 6x,y 4y B(6x,4y) 1 1 将点B(6x,4y)代入直线l，可得4y3(6x)3， 3xy170 3xy170 整理得 ，即对称直线的方程为 . y3x3 5 9  x ,y (2)由xy20，解得 2 2， 5 9 E( , ) 即直线xy20与 y3x3 的交点坐标为 2 2 ， 再在直线xy20上取一点C(0,2)， 设点C关于直线y3x3的对称点为N(m,n)， n2 31  m0 则 ，解得 ，即 ， n2 m0  3 3  2 2 m3,n1 N(3,1) 9 1( ) 2 k  7 又由 EN 5 ，所以直线 的方程为 ， 3( ) 2 EN y(1)7[x(3)] 整理得7xy220， xy20 7xy220 即直线 关于直线l对称的直线的方程为 . 1 y x1 47．（2022·江苏·高二课时练习）已知直线l: . 2 (1)求点P（3， 4)关于直线l对称的点Q； (2)求直线l关于点（2， 3)对称的直线方程． 【解析】(1)设Q（x y)． 0， 0 由于PQ⊥l，且PQ的中点在直线l上，  y 4  29   x 0 3 2,   x 0  5 , 则 0 ，解得 ，所以Q . y 0 4  1  x 0 3 1. y  8 .   29 , 8   2 2 2  0 5  5 5(2)在直线l上任取一点，如M（0， －1). 设点M关于点（2， 3)对称的点为N（x， y)， 0x4 x4   所以1y6，解得：y7，所以N（4， 7) 1 k＝ 因为所求直线与l平行，所以 , 2 1 y－7＝ x－4 所以所求的直线方程为 ，即x－2y＋10＝0. 2 核心知识6 直线中的范围与最值问题 A4,2 48．（2022·湖北·监利市教学研究室高二期末）已知定点 ，动点M､N 分别在直线yx和y0上运 动，则 AMN 的周长取最小值时点N 的坐标为__________. 10  【答案】 ,0  3  【解析】如图所示： 定点 A4,2 关于函数yx的对称点 B2，4 ，关于x 轴的对称点 C4，2 ， 当BC与直线yx和y0的交点分别为M,N时，此时 AMN 的周长取最小值，且最小值为  BC  (24)2422 2 10 ． x2 04 此时点Nx,0的坐标满足  ， 42 2410 解得x ， 3 10  N ,0 即点  3 . 10   ,0 故答案为： 3 . l ,l 49．（2022·北京十五中高二期中）已知直线 1 2均过点P(1，2). l l l l (1)若直线 1过点A(-1，3)，且 1 2求直线 2的方程； 2 Q(0, 2) (2)如图，O为坐标原点，若直线l 1 的斜率为k，其中 0k 2 ，且与y轴交于点N，直线l 2 过点 R2 ， l ,l 且与x轴交于点M，求直线 1 2与两坐标轴围成的四边形PNOM面积的最小值. l ,l l 【解析】(1)因为直线 1 2均过点P(1，2)，且直线 1又过点A(-1，3)， 1 所以k l1  2 ，因为l 1 l 2 ， k 2 l y22x1 y2x 所以 l2 ，则直线 2的方程 ，即 ； (2)如图所示：l y2kx1 由题意得：直线 1的方程为： ，   x0 y2k N 0,2k 令 ，得 ，即 ， 2  2  x 1 T  1,0 令y0，得 k ，即直线l 与x轴的交点为  k ， 1 2 Q(0, 2) 直线l 2 又过点 R2 ， 2  2 2 所以直线 的方程为：y 2  R2  x 1 ， l 2 0  1 2   即y 2   x 1 ， R2   MR2  1,0 令y0，得x  R2  1，即 ， 1  2  1 2  S  S S  R2  1   1  2    1   2k  所以 PNOM TPM TNO 2  k  2 k  ， 2 1  2k 2  R2   ， k 2 k k  R2   2， 2 因为0k 2， k 2 R2  1 所以当 时， PNOM面积的最小值为 . 50．（2022·全国·高二期末）数学家华罗庚说：“数缺形时少直观，形少数时难入微”，事实上，很多代 xa2 yb2 数问题可以转化为几何问题加以解决．例如：与 相关的代数问题，可以转化为点 Ax,y Ba,b f x x2 2x2 x2 2x2 与点 之间的距离的几何问题．结合上述观点：对于函数 ， f x 的最小值为______．2 2 【答案】 f x x22x2 x22x2  x121 x12 1 【解析】函数 ， Px,0 E1,1 F1,1 表示点 与点 与 距离之和的最小值，则点P在 x 轴上， E1,1 E x 点 关于 轴的对称点 ， PEPF PEPF EF  1+12+1+12=2 2 所以 ， f x 2 2 所以 的最小值为： . 2 2 故答案为： . l :kxyk20 l :kxy30 51．（2022·四川巴中·高二期中（文））当实数k变化时，直线 1 到直线 2 的 距离的最大值是______. 26 【答案】 k(x1)y20 l A(1,2) kxy30 l B(0,3) 【解析】由 可得 1过定点 ，由 可得 2过定点 . 又两直线斜率相等，可知两直线平行且垂直于AB时，距离最大，最大值即为AB两点间的距离 d  1252  26 . 26 故答案为： . M(a,b) 5x12y260 a2b2 52．（2022·上海虹口·高二期末）已知点 在直线 上，则 的最小值为 ________． 【答案】2 a2b2 (0,0) M(a,b) 【解析】 可以理解为点 到点 的距离， 又∵点M(a,b)在直线5x12y260上， a2b2 (0,0) 5x12y260 ∴ 的最小值等于点 到直线 的距离，|5012026| d  2 且 52122 . 故答案为：2. a2x1ay60 O l 53．（2022·四川南充·高二期末（文））过坐标原点 作直线 ： 的垂线，垂足为 Hs,t s2t2 ，则 的取值范围是（ ） 0,2 2  0,2 2 0,8 0,8 A．  B．  C． D． 【答案】D (a1)s(a2)t 0    【解析】依题意，OH (s,t)，直线l的方向向量n(a1,a2)，则有(a2)s(a1)t 6，  6(a2) s   (a2)2(a1)2 36 36 解得 ，因此，s2t2   ， t  6(a1) (a2)2(a1)2 2(a 1 )2 9   (a2)2(a1)2 2 2 36 0 8 1 1 9 9 1 9 因当a 时，2(a )2 取最小值 ，则有 2(a )2 ， 2 2 2 2 2 2 s2t2 (0,8] 所以 的取值范围是 . 故选：D mR A xmy10 B 54．（2022·湖南·益阳平高学校高二期中）设 ，过定点 的动直线 和过定点 的动直线 mxy2m30 Px,y PA  PB 交于点 ，则 的最大值（ ） 2 5 3 2 A． B． C．3 D．6 【答案】D 【解析】由题意，动直线xmy10过定点A(1,0)， x20  直线mxy2m30可化为(x2)m3 y 0，令3y0，可得B(2,3)，又1mm(1)0，所以两动直线互相垂直，且交点为P， |PA|2 |PB|2|AB|2122 032 18 所以 ， |PA|2 |PB|2 |PA||PB| 2   因为 2  2  ， PA  PB  2  |PA|2 |PB|2  218 6 所以 ，当且仅当|PA||PB|3时取等号. 故选：D. M axy20 N 55．（2022·四川·遂宁中学高二期中（理））过定点 的直线 与过定点 的直线 xay4a20 PM·PN P 交于点 ，则 的最大值为( ) A．1 B．3 C．4 D．2 【答案】C axy20 M0,2 【解析】由题意可知，动直线 经过定点 ， xay4a20 x2y4a0 N2,4 动直线 即 ，经过定点 ， ∵过定点M 的直线axy20与过定点N 的直线xay4a20始终垂直，P又是两条直线的交点， 2 2 2 PM  PN  MN 8 ∴PM PN ，∴ ． PM 2 PN 2 PM  PN  4 故 2 (当且仅当 PM  PN 2时取“”)． 故选：C． 56．（2022·安徽省六安中学高二期中（文））已知 A(0,2),B(3,1) ，点P为 x 轴上一动点，则 PA  PB 的 最大值是（ ） 10 3 2 2 2 7 A． B． C． D． 【答案】A 【解析】由已知点A关于x轴的对称点为C(0,2)， 12 1 1 k   y  x2 ，直线 方程为 ，令 得 ， BC 30 3 BC 3 y0 x6所以直线BC与x轴交点为Q(6,0)， PA  PB  PC  PB  CB  (30)2(12)2  10 ，当且仅当P是BC与x轴交点 Q 时等号成立． 故选：A． 4,3 57．（2022·湖北荆州·高二期中）（1）求过点 且在两坐标轴上截距相等的直线l的方程； a1xy2a0aR a1 （2）设直线l的方程为 ，若 ，直线l与x，y轴分别交于M，N两点，O 为坐标原点，求 OMN 面积取最小值时，直线l的方程． x y 【解析】（1）当直线不过原点时，设l的方程为 ＋ ＝1， a a 4 3 ∵点4,3在直线上，∴ ＋ ＝1， a a 解得a1，所以直线方程为x＋y－1＝0； 3 3 当直线过原点时，直线斜率k  ，∴直线的方程为y x，即3x＋4y＝0. 4 4 综上知，所求直线方程为x＋y－1＝0或3x＋4y＝0. a2 （2）∵ a1 ，∴M ( a1 ,0) ，N0,2a， S  1  a2 2a 1    a11  2 1  a1 1 2   ∴ OMN 2 a1 ＝2 a1 ＝ 2  a1 ≥2， 1 当且仅当a＋1＝ ，即a＝0时等号成立． a1 故所求直线l的方程为x＋y－2＝0.58．（2022·四川巴中·高二期中（文））已知直线l过点（1，2）. (1)若直线l与2xy10平行，求直线l的方程； (2)若直线l与x轴正半轴交于A点，与y轴正半轴交于B点，O为坐标原点，求 AOB的面积的最小值. 【解析】(1)因为直线l与2xy10平行，所以直线l的斜率为2， 又直线l过点（1，2）， l y22x1 2xy0 所以直线 的方程为 ，即 ； l l:y- 2=k(x- 1) k 0 (2)由题意，直线 的斜率存在，设 ，且 ，  2  令 y0 ，可得A  1 k ,0  ，令 x0 ，可得 B0,2k， S  1   1 2 2k2 1 k 4   2 1 2 k   4  4 k  4 所以 AOB 2  k 2 k 2  k ，当且仅当 k ，即 k 2时等号成立， 所以 AOB的面积的最小值为4. Mx,x1 N1,1 MN 59．（2022·黑龙江·齐齐哈尔市第八中学校高二期中）设 ， ，则 的最小值为 xy10 d  x2y26x10y34 x2y24x30y229 ______；已知x、y满足 ，若 ，则d的最小 值______． 3 2 【答案】 2 【解析】因为M(x,x1)，N(1,1)， 1 9 9 3 2 则|MN| (x1)2(x11)2  2x22x5 2(x )2 �  ， 2 2 2 2 3 2 即 的最小值为 ； |MN| 2 d  x2y26x10y34 x2y24x30y229  (x3)2(y5)2  (x2)2(y15)2 ， 可看作点A(3,5)和B(2,15)到直线xy10上的点的距离之和， A(3,5)关于直线xy10的对称点设为A(x ，y )， 0 03x 5y 0  0 10   2 2 则 ，解得 ， ， y 5  0 1 x 3 x 4 y 2 0 0 0 所以A的坐标为(4,2)， |AB| (24)2(152)2  293 则d的最小值为 ． 3 2 故答案为： ； ． 2 293 核心知识7 圆的方程 60．（2022·河北唐山·高二期中）圆心在直线2x－3y－1＝0上的圆与x轴交于A（1，0）、B（3，0）两点， 则圆的方程为________． (x2)2(y1)2 【答案】 ＝2 【解析】由题意得：圆心在直线x2上， 又圆心在直线2x3y10上，令x2，得y1 圆心M 的坐标为(2,1)，又A(1,0)， |AM| (21)2(10)2  2 半径 ， (x2)2(y1)2 2 则圆的方程为 ． (x2)2(y1)2 2 故答案为： x22y12 5 xy0 61．（2022·上海市第三女子中学高二期末）圆 关于直线 对称的圆的方程为 ______． x12y22 5 【答案】 x22y12 5 2,1 5 【解析】圆 的圆心为 ，半径为 ； 2,1 xy0 1,2 圆心 关于直线 对称的点为 ， x12y22 5 所以所求圆的方程为 .x12y22 5 故答案为： . xy2 xy0 C(1,1) 62．（2022·上海金山·高二期中）过直线 与直线 的交点， 圆心为 的圆的标准 方程是_____. (x1)2(y1)2 4 【答案】 xy2 x1   【解析】由xy0，得y1， 所以直线 xy2 与直线 xy0 的交点为(1,1)， (11)2(11)2 2 所以圆的半径为 ， (x1)2(y1)2 4 所以所求圆的标准方程为 ， (x1)2(y1)2 4 故答案为： C6,8 O OC 63．（2022·全国·高二期中）已知点 ， 为坐标原点，则以 为直径的圆的方程是______． x32y42 25 【答案】 C6,8 O0,0 【解析】由题意可知， ， ， 所以以OC的中点坐标为E3,4 ， OE  302402  25 5 ， x32y42 25 OC 所以以 为直径的圆的方程为 . x32y42 25 故答案为： . x2y24mx2y5m0 m 64．（2022·全国·高二期中）方程 表示圆，则 的取值范围为______． 1 m 【答案】 或 4 m>1 1 【解析】由题意知：4m2(2)245m0，即 4m25m10 ，解得 m 4 或 m>1 .1 m 故答案为： 或 . 4 m>1 x2y24x4y40 l:xy20 65．（2022·贵州·遵义四中高二期末）圆 关于直线 的对称圆的标准方 程为_______． x2y2 4 【答案】 x2y24x4y40 x22y22 4 【解析】圆 的标准方程为 ， 圆心(2,2),半径为2， l:xy20 O0,0 圆心(2,2)关于直线 的对称点为原点 , x2y2 4 所以所求对称圆的标准方程为 ， x2y2 4 故答案为： A(0,0),B(2 3,0),C(0,2) 66．（2022·北京十五中高二期中）经过三个点 的圆的方程为（ ）  x 3 2 y12 2  x 3 2 y12 2 A． B． C．  x 3 2 y12 4 D．  x 3 2 y12 4 【答案】C A(0,0),B(2 3,0),C(0,2) x y 【解析】由已知得， 分别在原点、 轴、 轴上，  AB AC，经过三点圆的半径为r 1 BC  1  2 30 2 022 2，  2 2 2 30 02 圆心坐标为 的中点   2 , 2  ，即  3,1  ， BC    x 3 2 y12 4 圆的标准方程为 . 故选：C. A0，10，B6，10 2xy1 67．（2022·福建宁德·高二期中）某圆经过 两点，圆心在直线 上，则该圆的标 准方程为（ ） x32 y52 34 x32 y52 34 A． B． x32 y52 34 x32 y52 34 C． D． 【答案】D A0，10，B6，10 【解析】因为圆经过 两点， 06 所以圆心在中垂线x 3上， 2 x3  联立2xy1解得圆心(3,5)，所以圆的半径R 32(510)2  34 ， x32 y52 34 故所求圆的方程为 ， 故选：D x2y2kx2y4 68．（2022·河北唐山·高二期中）点M，N是圆 ＝0上的不同两点，且点M，N关于直 线x－y＋1＝0对称，则该圆的半径等于（ ） 2 2 2 A． B． C．3 D．9 【答案】C k k2 【解析】圆 ＝0的标准方程为（x＋ ）2＋（y＋1）2＝5＋ ， x2y2kx2y4 2 4k k2 r 5 则圆心坐标为（－2，－1），半径为 4 x2y2kx2y4 因为点M，N在圆 ＝0上，且点M，N关于直线l：x－y＋1＝0对称， 所以直线l：x－y＋1＝0经过圆心， k 所以－ ＋1＋1＝0，k＝4． 2 k2 r 5 所以圆的方程为：x2y24x2y4＝0，圆的半径 4 ＝3. 故选：C． x2y2mx2y20 69．（2022·四川·泸县五中高二期中（文））已知点A（1，2）在圆C： 外，则实 数m的取值范围为（ ） 3,2 2, 3,23,  A． B． 2, 3, C． D． 【答案】A x2y2mx2y20 【解析】由题意， 表示圆 m2(2)2420 m2 m2 故 ，即 或 x2y2mx2y20 点A（1，2）在圆C： 外 故1222m2220，即m3 故实数m的取值范围为m2或3m2 m3,2 2,  即 故选：A 70．（2022·内蒙古·包头市第四中学高二期中）已知点A(4,2)和B(0,2) (1)求直线AB的方程； (2)若圆C经过A,B两点，且圆心在直线2xy3上，求圆C的方程k 1 xy20 AB 【解析】(1) ，故直线方程为 . a,b (2)设圆心 C 为 ，半径为r, 2xy3 2ab3 C a,2a3 圆心在直线 上， ，则点 为 , AC  BC 由题意可得 可得： a42 2a322  a02 2a322 5 1 74 解得a ，b ，r  ， 3 3 3  5 2  1 2 74 x  y   圆C的标准方程为 3  3 9 . 71．（2022·福建·厦门大学附属科技中学高二期中）已知 ABC的三个顶点分别为 A4,0,B0,2,C2,2 ，求： (1)AB边中线所在的直线方程 (2) ABC的外接圆的方程 3  【解析】(1)设 AB 的中点为D(2,1)，则 CD 所在直线的斜率为 4 ， 3 则 边所在直线的方程为y1 (x2)，即 ． CD 4 3x4y20 ABC x2y2DxEyF 0  (2)设 的外接圆的方程为 ， 4DF160 D2   2EF40 E2 由 ，解之可得   2D2EF80 F 8 ABC x2 y22x2y80  故 的外接圆的方程为 ． 核心知识8 轨迹方程 xOy yx22x3 72．（2021·安徽省六安中学高二期中（文））在平面直角坐标系 中，曲线 与两坐标轴的交点都在圆C上. (1)求圆C的方程； (2)已知O为坐标原点，点A在圆C上运动，求线段OA的中点M 的轨迹方程. yx22x3 【解析】(1)由 ， 令y0，解得x1或x3；令x0，得y3， 0,3,3,0,1,0 C 所以圆 过 . 设圆C的方程为x2y2DxEyF 0， 93EF 0  93DF 0 ，解得 ，  1DF 0 D2,E2,F 3 C x2y22x2y30 所以圆 的方程为 . Mx,y A2x,2y (2)设 ，则 ， A C 4x24y24x4y30 将 的坐标代入圆 的方程得 ， 3 即 x2y2xy 0 . 4 O(0,0) A(3,0) 73．（2021·安徽·合肥市第六中学高二期中（理））已知动点P与两个顶点 ， 的距离的比值 为2，点P的轨迹为曲线C． (1)求曲线C的轨迹方程;   B(0,3) OM ON 9 (2)过点 且斜率为k的直线l，交曲线C于、N两点，若 ，求斜率k P(x,y) |PO|2|PA| x2y2 4[(x3)2y2] 【解析】(1)设点 ，依题意， ，则 ，化简整理得： (x4)2y2 4 ， (x4)2y2 4 所以曲线C的轨迹方程是： .ykx3  (2)依题意，设直线l的方程为：ykx3，由(x4)2y2 4消去y并整理得： 21 21 ，由 得1 k 1 ， (k21)x22(3k4)x210 4(3k4)284(k21)0 6 6 6k8 21 设 ， ，则有x x  ,xx  ， M(x,y) N(x ,y ) 1 2 k21 1 2 k21 1 1 2 2   OMON xx y y xx (kx 3)(kx 3)(k21)xx 3k(x x )99 1 2 1 2 1 2 1 2 1 2 1 2 ， 21 6k8 即(k21) 3k 0，整理得 ，解得 或 （舍去）， k21 k21 k28k70 k 1 k 7 所以斜率k 1. 74．（2020·四川巴中·高二期中（文））已知圆C经过点A（3，1）、B（－1，3），且它的圆心在直线 3xy20 上. (1)求圆C的标准方程； (2)若点D为圆C上任意一点，且点E（3，0），求线段ED中点M的轨迹方程. xa2yb2 r2 【解析】(1)由题可设圆C的标准方程为 ，则 3a2 1b2 r2    1a2 3b2 r2 ，  3ab20  a  2,b  4, r2  10 解之得 ， x22y42 10 所以圆C的标准方程为 ；  x 3 x 1   2 (2)设M（x，y），D ，则，由E(3，0)及M为线段ED的中点得： ，解得x 2x3   y y 1 0  1 x,y  2 y 2y 1 1 1 (x2)2(y4)2 10 又点D在圆C： 上， 2x3222y42 10 所以有 ， x 5  2 y22  5 化简得： 2 2．  x 5  2 y22  5 故所求的轨迹方程为 2 2． 75．（2021·四川巴中·高二期中）已知圆C经过（-1，3），（5，3），（2，0）三点. (1)求圆C的方程；  15 B8,    (2)设点A在圆C上运动，点  2 ，且点M满足AM 2MB，求点M的轨迹方程. x2y2DxEyF 0 【解析】(1)设圆C的方程为 12 32D3EF 0 D4  则有 52325D3EF 0 ，解之得  E6   22022DF 0  F 4 x2y24x6y40 则圆C的方程为 M(x,y) A(x ,y ) A A (2)设 ， ，  15 则有  A  M  (xx ,yy )，MB(8x, 2 y)， 2M  B  (162x,152y) A A xx 162x x 163x A A   由 A  M  2M  B ，可得yy A 152y，解之得y A 153y 163x2 153y2 4163x6153y40 由点A在圆C上，得 x2y212x12y710 即 x2y212x12y710 故点M的轨迹方程为 . A0,2 76．（2022·福建龙岩·高二期末）已知平面直角坐标系上一动点P满足：到点 的距离是到点 B0,1 的距离的2倍. (1)求点P的轨迹方程；Q xy20 PQ (2)若点P与点 关于直线 对称，求 的最大值. P(x,y) 【解析】(1)设 ，由题意，得： x2y22 2 x2(y1)2 ， x2y24y0 化简得 ， x2y24y0 P 所以点 的轨迹方程为 Qx,y Q xy20 P (2)方法一：设 ，因为点 与点 关于点 对称， 则P点坐标为(y2,x2)， x2y24y0 x2 (y2)2 4 P 因为点 在圆 ，即 上运动， (x4)2(y2)2 4 所以 ， Q (x4)2(y2)2 4 所以点 的轨迹方程为 ， 0,2,4,2 所以两圆的圆心分别为 ，半径均为2， |PQ|  (04)2(22)2 44 24 则 max . x2y24y0 x2 (y2)2 4 方法二：由 可得： 0,2 所以点P的轨迹是以 为圆心，2为半径的圆 022 d  2 2 轨迹P的圆心到直线xy20的距离为： 2 |PQ| 2d2r4 24 max C:x2(y2)2 5 l:mxy10 77．（2021·四川省绵阳南山中学高二期中（理））已知圆 ，直线 . (1)判断直线l与圆C的位置关系； (2)若圆C与直线l相交于点A和点B，求弦AB的中点M 的轨迹方程.l:mxy10 D0,1 【解析】(1)直线 经过定点 ， 0,2 D 5 点 到圆心 的距离等于1小于圆的半径 ， 0,1 l C 故定点 在圆的内部，故直线 与圆 总有两个不同交点，故直线和圆相交； x,y M ABCM (2)设中点 的坐标为 ，则由直线和圆相交的性质可得 . D0,1 C M 由于定点 ､圆心 ､点 构成直角三角形， CM 2  DM 2  CD2 由勾股定理得 ， x2(y2)2x2(y1)2 (21)2 ，  3 2 1 x2y   ∴2x22y26y40，即  2 4， 0,2 l 由于直线 的斜率一定存在，故排除圆上的点 . C:x2(y2)2 5 此圆在圆 的内部，  3 2 1 故点 M 的轨迹方程为： x2  y 2    4，除去点 0,2 . Mx,y O0,0 A3,0 78．（2022·四川雅安·高二期末（理））已知坐标平面上动点 与两个定点 、 ，且 1 MO  MA ，设动点 的轨迹为曲线 . 2 M C x 3y20 C P Q PQ (1)若直线 与曲线 交于 、 两点，求 的长； B3,2   (2)若点 与动点M 所连线段上有一点E，满足BE3EM ，求点E的轨迹方程. 【解析】(1) MO  x2y2 ， MA  x32y2 1  MO  MA ，即2 MO  MA ，所以，2 x2+y2 = ( x-3)2 +y2 2x12 y2 4 1,0 化简为 ，所以，曲线 C 是以点 为圆心，半径r 2的圆， 12 1 1 d   PQ 2 4  15 圆心到直线x 3y20的距离 2 2，所以， 4 . Ex,y M  x,y   B  E  x3,y2  E  M  x x,y y (2)设 、 0 0 ，则 ， 0 0 ，   x3,y23x x,y y 因为 BE3EM ，则 0 0 ，  4x3 x    0 3 即   x y   3 2   3 3   x y 0 0   x y   ，可得   y 0  4y 3 2 ， 4x3  2 4y2 2  1 2 9 因为 x 0 12 y 0 2 4，所以，   3 1    3   4 ，化简得 x2  y 2    4，  1 2 9 x2y   所以点E的轨迹方程为  2 4. C :x2y2 1 C :xa2yb2 1 79．（2022·广西柳州·高二期中（理））若圆 1 与圆 2 的公共弦AB的长 为1，则下列结论正确的有（ ） A．a2b2 1 a2b2 14 B． 3 x2y2  C． 中点的轨迹方程为 AB 4 9 x2y2  D． 中点的轨迹方程为 AB 16 【答案】C a2b22ax2by0 【解析】两圆方程相减可得直线AB的方程为 ， 2ax2bya2b2 0 即 ， C C 0,0 因为圆 1的圆心为 1 ，半径为1，C 0,0 且公共弦AB的长为1，则 1 到直线 3 2ax2bya2b2 0的距离为 2 ， a2b2 3  所以 4  a2b2 2 ，解得 ， a2b2 3 故A、B错误； CC 由圆的性质可知直线 1 2垂直平分线段 AB ， C 0,0 2ax2bya2b2 0 所以 1 到直线 的距离 C x,y 即为AB中点与点 1的距离，设AB中点坐标为 ， 3 因此 x02y02  ， 2 3 x2y2  即 ，故C正确，D错误； 4 故选：C 80．（2022·上海·位育中学高二期末）已知圆C过三个点M(1,0),N(3,2),R(5,0). (1)求圆C的方程； (2)过原点O的动直线l与圆C相交于不同的A,B两点，求线段AB的中点M 的轨迹. C x2y2DxEyF 0(D2E24F 0) 【解析】(1)设圆 的方程为 ， 因为圆C过三个点M(1,0),N(3,2),R(5,0)， 1DF 0  943D2EF 0 可得 ，解得 ，  255DF 0 D6,E0,F 5 C x2y26x50 (x3)2y2 4 所以圆 的方程为 ，即 . (2)因为M 为线段AB的中点，且CM OM ，所以M 在以OC为直径的圆上， 3 9 (x )2y2  以OC为直径的圆的方程为 2 4 ， 5  5 x32 y2 4  x  x   3  3 联立方程组   x 3  2 y2  9 ，解得  y 2 5 或  y 2 5 ，  2 4  3  3 3 9 5 (x )2y2  ,( x3) 所以点 的轨迹方程为 . M 2 4 3 核心知识9 直线与圆的位置关系 x2y24x4y70 xay20 81．（2022·黑龙江·齐齐哈尔市恒昌中学校高二期中）已知圆 与直线 相 切，则a___________. 3 【答案】 3 x2y24x4y70x22y22 1 【解析】 ， 圆的圆心为(2，－2)，半径r＝1， 2a22 3 1a ∵圆和直线相切，∴ 1a2 3 . 3  故答案为： 3 . (x1)2(y1)2 4 xmym20 82．（多选题）（2022·云南曲靖·高二期末）已知圆 与直线 ，则 （ ） A．直线与圆必相交 B．直线与圆不一定相交 2 3 C．直线与圆相交所截的最短弦长为 D．直线与圆可以相切 【答案】AC (x1)2(y1)2 4 C1,1 r 2 【解析】由题意，圆 的圆心 ，半径 ， xmym20 x2my10 A2，1 直线 变形得 ，得直线过定点 ， CA  212112 12 ∵ ， ∴直线与圆必相交，故A对，B、D错； 由平面几何知识可知，当直线与过定点A和圆心的直线垂直时，弦长有最小值，2 r2 CA2 2 3 此时弦长为 ，故C对； 故选：AC． l:xy10 C:x2y2 1 83．（多选题）（2022·广东深圳·高二期末）已知直线 ，圆 ，则（ ） A．直线l与圆C相交 C l 2 B．圆 上的点到直线 距离的最大值为 C．直线l关于圆心C对称的直线的方程为xy10 C l x12y12 1 D．圆 关于直线 对称的圆的方程为 【答案】ACD C C0,0 r1 【解析】由圆 方程知：圆心 ，半径 ； 1 2 d   1 对于A， 圆心C到直线l距离 2 2 ，直线l与圆C相交，A正确；  2 2 d  dr  1 对于B， 圆心C到直线l距离 2 ，圆C上的点到直线l距离的最大值为 2 ，B错误；  l C xym0m1 对于C，设直线 关于圆心 对称的直线方程为： ， m 2   则圆心C到直线l和到其对称直线的距离相等， 2 2 ，解得：m1（舍）或m1，直线l关于圆 心C对称的直线的方程为xy10，C正确； b 1  a 对于D，设圆心 关于直线 对称的点为 ，则 a b ，解得：a1， C l a,b  2  2 10  b1 所求圆的圆心为1,1，半径为1， 圆 C 关于直线 l 对称的圆的方程为 x12y12 1 ，D正确. 故选：ACD. axy20aR x12y12 4 84．（多选题）（2022·广东汕尾·高二期末）直线l： 与圆 C ： 相交于A，B两点，则（ ） 0,2 l A．直线 过定点 B．a2时，直线l平分圆C C．a1时， ABC为等腰直角三角形 D．a1时，弦AB最短 【答案】AD x0 y2 l 0,2 【解析】对A，因为当 时， 恒成立，故直线 过定点 ，故A正确； a2 2xy20 C 1,1 2xy20 l C 对B，当 时， ，圆 的圆心为 不满足 ，故此时直线 不过圆 的圆心，故 直线l不平分圆C，故B正确； a1 xy20 C 1,1 ABC 对C，当 时， 经过圆 的圆心 ，故无 ，故C错误； P0,2 012212 24 P0,2 对D，因为直线l过定点 ， ，故 在圆内，故当弦AB最短时，CP与直 21 1 线 垂直.因为 时，直线 的斜率为 ，直线 的斜率为1，故 与直线 垂直成立，故D正 l a1 CP 01 l CP l 确； 故选：AD P2,1 x2y2 1 85．（多选题）（2022·江苏·东海县教育局教研室高二期中）过点 作圆O： 的两条切线， 切点分别为A，B，则下列说法正确的是（ ） PA  3 x2y2 2xy A． B．四边形PAOB的外接圆方程为 8 C．直线AB方程为y=2x+1 D．三角形PAB的面积为 5 【答案】BD  2 【解析】对A， PO  2212  5，由勾股定理， PA  5 12 2.A错误；  1 1,  5 对B，由题意可知，PBOB，则PO为所求圆的直径，线段PO的中点为 2，半径为 2 ，于是，所求x12  y 1  2  5 x2y2 2xy 圆的方程为：  2 4 .B正确； 1 对C，由题意，其中一个切点的坐标为0,1，不妨设为点B，则 ABOP ，而 k OP  2 ，则k 2，于是， AB y2x1 直线AB的方程为： .C错误； 1 2 1 对D，易知 ，因为l :y x， ，联立解得两条直线的交点D , ，则 PO AB OP 2 l :y2x1 5 5 AB 2 2 1  2 2 5 2  2 1  2 4 5 |BD|  5    5 1   5 ， |PD|  5 2   5 1   5 ， 1 4 5 2 5 4 8 所以三角形 的面积为：    ，则三角形PAB的面积为 . PBD 2 5 5 5 5 故选：BD. m2x2m1y3m10 86．（多选题）（2022·湖北恩施·高二期末）已知直线l： 与圆C： x22y12 16 交于A，B两点，则弦长|AB|的可能取值是（ ） A．6 B．7 C．8 D．5 【答案】BC m2x2m1y3m10 x2y3m2xy10 【解析】由 ，得 ， x2y30 x1,   令2xy10 解得y1,故直线l恒过点M(1,1).圆心C(2,1)，半径r 4， CM  122112  5 2 r2 CM 2  AB 2r ，则 ， 2 11 AB 8 即 . 故选：BC. 87．（多选题）（2022·福建·南靖县第一中学高二期中）下列说法正确的是（ ） P1,2 x y xy30 A．过点 且在 、 轴截距相等的直线方程为1,2 x2y30 2xy0 B．过点 且垂直于直线 的直线方程为 x2 y26x4y0 x2y24x2y40 xy20 C．过两圆 及 的交点的直线的方程是  5 3 , D．直线 ykx24 与曲线y=1+ 4- x2 有两个不同的交点，则实数k的取值范围是  12 4   【答案】BC 【解析】对于A选项，当直线过原点时，设直线的方程为ykx，则有k 2，此时所求直线方程为y2x， xyaa0 a123 xy30 若直线不过原点，设所求直线方程为 ，则 ，此时所求直线方程为 ， P1,2 x y y2x xy30 所以，过点 且在 、 轴截距相等的直线方程为 或 ，A错； 1 x2y30 对于B选项，直线 的斜率为2 ， 1,2 x2y30 y22x1 2xy0 所以，过点 且垂直于直线 的直线方程为 ，即 ，B对； x2 y26x4y0 x32y22 13 A3,2 对于C选项，圆 的标准方程为 ，圆心为 ，半径为 r  13 1 ， x2y24x2y40 x22y12 9 B2,1 r 3 圆 的标准方程为 ，圆心为 ，半径为 2 ，  AB  322212  2 ，r r  AB r r ，故两圆相交， 1 2 1 2 将两圆方程作差得xy20， x2 y26x4y0 x2y24x2y40 xy20 所以，过两圆 及 的交点的直线的方程是 ，C对； y=1+ 4- x2 �1 y-1= 4- x2 x2y12 4 对于D选项，由 可得 ，得 ， y=1+ 4- x2 x2y12 4 所以曲线 表示圆 的上半圆， ykx24 E2,4 k 直线 表示过点 且斜率为 的直线，如下图所示：ykx24 y=1+ 4- x2 当直线 与半圆 相切且切点位于第二象限时，  32k  2  k21 5 则 ，解得 ；  k  k 0 12 3 当直线ykx24过点F2,1时，则 4k41 ，解得 k  4 . 纟5 3 由图可知，直线 ykx24 与曲线 y=1+ 4- x2 有两个不同的交点，则实数 k 的取值范围是�� 棼12 , 4 � � ， D错. 故选：BC. l xy40 C x2y2 8 88．（2022·广东江门·高二期末）直线 ： 与圆 ： 的位置关系为（ ） A．相切 B．相交 C．相离 D．不确定 【答案】A C x2y2 8 0,0 r2 2 【解析】圆 ： 的圆心为 ，半径 ， 4 d  2 2 r 圆心到直线 l ： xy40 的距离 1212 ， 所以直线与圆相切； 故选：A kxykt 0 x2y2 10 89．（2022·广西梧州·高二期末（文））已知对任意的实数k，直线l： 与圆C： 有公共点，则实数t的取值范围为（ ）[3,0) [3,3] A． B． (,3] (0,3] (,3) [0,3]   C． D． 【答案】B 【解析】由直线kxykt 0可化为ytk(x1)，则直线l过定点(1,t)， kxykt 0 x2y2 10 因为直线l： 与圆C： 有公共点， (1,t) 12t2 10 3t3 所以定点 在圆C上或圆C内，可得 ，解得 ， 故选：B C:x2  y2 8x6y210 90．（2022·吉林辽源·高二期末）已知过坐标原点O的直线与圆 相切，则切 线长（点O与切点间的距离）为（ ） 21 A．3 B．4 C． D．5 【答案】C x42y32 4 【解析】圆C的标准方程为 ， C4,3 r 2 圆心 ，半径 ， OC 5 L OC2r2  5222  21 所以 ，切线长为 . 故选C. l:xay10(aR) C:x2y24x2y10 91．（2022·安徽·屯溪一中高二期中）已知直线 是圆 的对称 A(4,a) C B D BD 轴.过点 作圆 的两条切线，切点分别为 、 ，则直线 的方程为（ ） 3xy50 2x y50 3xy50 2x y50 A． B． C． D． 【答案】A x22 y12 4 【解析】根据题意，圆C的标准方程为 ，即圆心为 C(2,1)，半径为2.  xay10 2a10a1 点(2,1)在直线 上，即点A的坐标为(-4,-1) AC  242 112 2 10  AC222 6 过点A作圆C的切线所得切线长为 x42 y12 36 以点A为圆心，6为半径的圆A的方程为 3xy50 3xy50 圆A与圆C的方程作差得 ，即直线BD的方程为 故选：A. y1kx3 x22y22 4 92．（2022·甘肃酒泉·高二期末（理））直线 被圆 所截得的最短弦长等 于（ ） 2 2 3 2 2 5 A． B． C． D． 【答案】C (x2)2(y2)2 4 C(2,2) r 2 【解析】圆 的圆心为 ，半径 ， 又直线y1k(x3)，直线恒过定点P(3,1)， 当圆被直线截得的弦最短时，圆心C(2,2)与定点P(3,1)的连线垂直于弦， (23)2(21)2  2 此时弦心距为 ． 2 22( 2)2 2 2 所截得的最短弦长： ． 故选：C． ykx1 x2y2 1 A，B AOB60 93．（2022·四川甘孜·高二期末（文））若直线 与圆 相交于 两点， 且 (其中O为原点)， 则k的值为（ ） 3 3 3  A． 3 或 3 B． 3 C． 2或 2 D． 2 【答案】A 3 【解析】由AOB60可知，圆心(0,0)到直线ykx1的距离为 2 ，根据点到直线的距离公式可得 1 3 3  k  12k2 2 31 3 3  k  12k2 2 3 故选：A x2y24x0 P(4,1). 94．（2022·湖北·高二期末）已知圆C： ，直线l恒过点 (1)若直线l与圆C相切，求l的方程； |AB|2 3 (2)当直线l与圆C相交于A，B两点，且 时，求l的方程. 【解析】(1)由题意可知，圆C的圆心为(2,0)，半径r 2， ①当直线l的斜率不存在时，即l的方程为x4时，此时直线与圆相切，符合题意；  y1k(x4) ②当直线l的斜率存在时，设斜率为k， 直线l的方程为 ， 化为一般式：kxy14k 0，若直线l与圆相切， |12k| 3 则d  2，即 ，解得k  ， k21 14k4k2 4k24 4 3  xy40 ： ，即l： ， l 4 3x4y160 综上，当直线l与圆C相切时，直线l的方程为x4或3x4y160； (2)由题意可知，直线l的斜率一定存在，设斜率为k，  y1k(x4) kxy14k 0 直线l的方程为 ，即 ， |12k| d  设圆心到直线l的距离为d，则 k21， |AB| (2k1)2 由垂径定理可得，d2( )2 4，即 34， 2 k21 4 k  整理得， ，解得 或 ， 3k24k 0 k 0 3 则直线l的方程为y1或4x3y130. A(4,1) B(3,2) 95．（2022·安徽·合肥市第六中学高二期中（理））圆心为C的圆经过点 和 ，且圆心C在直 线l:xy20上 (1)求圆心为C的圆的方程; (2)过点P(5,8)作圆C的切线，求切线的方程.【解析】(1)因圆心C在直线l:xy20上，则设C(a,a2)，由|CA||CB|得： (a4)2(a3)2  (a3)2(a4)2 ，解得a0，因此，圆心 C(0,2) ，半径 r|CA|5 ， x2(y2)2 25 所以圆C的方程为： . P(5,8) m(x5)n(y8)0 m2n2 0 (2)设过点 的圆C的切线方程为： ， ， |5m10n| 3 于是有： 5，整理得： ，解得 或m n， m2n2 4mn3n2 0 n0 4 3 m n 当 n0 时，切线方程为： x50 ，当 4 时，切线方程为：3x4y170， P(5,8) x50 3x4y170 所以过点 的圆C的切线方程为 或 . C :(x1)2(y2)2 9 C :(x2)2(y3)2 4 96．（2022·安徽·池州市第一中学高二期中）已知圆 1 ， 2 (1)判断两圆的位置关系，并求它们的公切线之长； (2)若动直线 l 与圆 C 1交于 P ， Q ，且线段 PQ 的长度为 2 6 ，求证：存在一个定圆 C ，直线 l 总与之相切. C :(x1)2(y2)2 9 C 1,2 r 3 【解析】（1）由圆 1 可得 1 ，半径 1 ， C :(x2)2(y3)2 4 C 2,3 r 2 由圆 2 可得 2 ，半径 2 ， CC  (12)2(23)2  2 1 2 ， 1r r  CC r r 5 C,C 所以 1 2 1 2 1 2 ，所以圆 1 2相交. 设直线 RS 分别与圆 C 1 ,C 2 切于 R ， S ，连接 C 1 R,C 2 S ， CC SR CR 3,C S 2,CC  2 在直角梯形 1 2 中， 1 2 1 2 ， |RS| CC 2r r 2 1 所以 1 2 1 2 ，即它们的公切线之长为1； （2）设线段 PQ 的中点为 D ，则 C 1 DPQ ， 因为动直线 l 与圆 C 1交于 P ， Q ，且线段 PQ 的长度为 2 6 ，|PQ| 2 2 6 2 所以 CD r2   32    3 ， 1 1  2   2  又因为 C 1 DPQ ，所以点 C 1 1,2 到直线 l 的距离为 3 ， l (x1)2(y2)2 3 所以直线 总与圆 相切， C:(x1)2(y2)2 3 l 所以存在一个定圆 ，直线 总与之相切. 核心知识10 圆与圆的位置关系 x2y2 1 xa2 y42 16 97．（2022·贵州黔东南·高二期末（理））若圆 与圆 有3条公切线，则正数 a=___________. 【答案】3 a242 5 a3,又a0,a3 【解析】两圆有三条公切线，则两圆外切，∴ ∴ 故答案为：3 98．（2022·山西吕梁·高二期末）写出一个同时满足下列条件①②③的圆C的标准方程：__________． x2y2 4 ①圆C的圆心在第一象限；②圆C与x轴相切；③圆C与圆 外切． 【答案】  x2 2 2 y12 1 (答案不唯一，但圆心坐标需满足a2 4b4， a0,b0 ) a,b a0,b0 r 0 【解析】设圆心坐标为 ，由①可知 ，半径为 ，  br  由②③可知  a2b2 r2 ，整理可得 a2 4b4 ，a0,b0 b1 a2 2 r1 当 时， ， ，  x2 2 2 y12 1 所以其中一个同时满足条件①②③的圆C的标准方程是 . 故答案为：  x2 2 2 y12 1 (答案不唯一，但圆心坐标需满足a2 4b4， a0,b0 ) x2y22x4y50 x2y22x10 A､B 99．（2022·上海市控江中学高二期中）已知圆 与 相交于 两点，则公共弦AB的长是___________. 【答案】2 【解析】由题意AB所在的直线方程为：  x2y22x4y5    x2 y22x1  0 ，即 y1 ， x2y22x10 O1,0 r 2 因为圆 的圆心 ，半径为 ， O1,0 y1 所以，圆心 到直线 的距离为1， AB 2 212 2 所以 . 故答案为：2 x2y2 1 x42 y32 16 100．（2022·广东广州·高二期末）写出与圆 和圆 都相切的一条切线方程 ___________. 【答案】y1或24x7y250或4x3y50 x2y2 1 O0,0 x42 y32 16 C4,3 【解析】圆 的圆心为 ，半径为1；圆 的圆心为 ，半径为4， OC 5 l,l ,l 圆心距为 ，所以两圆外切，如图，有三条切线 1 2 3， l y1 1 易得切线 的方程为 ， 3 4 4 k  k  l :y xb 因为l 3 OC，且 OC 4 ，所以 l3 3 ，设 3 3 ，即4x3y3b0， 3b 5 5 则 O0,0到 l 3 的距离 5 1，解得b 3 （舍去）或 3 ，所以 l 3 :4x3y50 ，  3 y x 可知 和 关于 3 对称，联立 4 ，解得 4 在 上， l 1 l 2 OC:y 4 x  y1    3 ,1  l 2 在 l 1上任取一点 0,1 ，设其关于 OC 的对称点为 x 0 ,y 0  ，   y 0 1  3  x 0  x  24  2 4 2   0 25 则 ，解得 ，  y 0 1    3 1 y  7  x  4  0 25 07  1 25 24 k   则 l2  24  4 7 ，所以直线 l :y1 24 x 4  ，即 ， 25 3 2 7  3 24x7y250 y1 24x7y250 4x3y50 综上，切线方程为 或 或 . y1 24x7y250 4x3y50 故答案为： 或 或 . C :x2y2 49 101．（2022·广东·汕头市潮阳区棉城中学高二期中）已知两圆分别为圆 1 和圆 C:x2y26x8y90 2 ，这两圆的位置关系是（ ） A．相离 B．相交 C．内切 D．外切 【答案】B C 0,0 C :x32y42 16 3,4 【解析】由题意得，圆 1圆心 ，半径为7；圆 2 ，圆心 ，半径为4， 3242 5 74574 两圆心之间的距离为 ，因为 ，故这两圆的位置关系是相交. 故选：B. O x2y2 5 O (x4)2y2 13 1 2 102．（多选题）（2022·江苏南通·高二期末）已知圆 ： 和圆 ： 相交于A， B两点，且点A在x轴上方，则（ ）|AB|4 A． O O 2 11 2 1 B．过 作圆 的切线，切线长为 O 3x2y10 2 C．过点A且与圆 相切的直线方程为 7 D．圆O 的弦AC交圆O 于点D，D为AC的中点，则AC的斜率为 2 1 2 【答案】ACD x2y2 5 x1   【解析】依题意，由 (x4)2y2 13解得 y2，则A(1,2),B(1,2)， O O(0,0) r  5 O O (4,0) r  13 圆 1的圆心 1 ，半径 1 ，圆 2的圆心 2 ，半径 2 ， |AB|4 ，A正确； O O |OO |2 r2  11 过 2作圆 1的切线，切线长为 1 2 1 ，B不正确； 20 2 3 3 直线AO 2 的斜率为k  14  3 ，过点A且与圆O 2 相切的直线斜率为 2 ，该切线方程为y2 2 (x1)， 即3x2y10，C正确； O OD AC OA x(x1)y(y2)0 1 1 1 因D为圆 的弦AC的中点，则 ，于是得点D在以线段 为直径的圆 上， x(x1)y(y2)0 7  而点D在圆O 2 上，则由(x4)2y2 13 得直线AD的方程7x2y30，其斜率为2，D正确. 故选：ACD 核心知识11 圆中的范围与最值问题 PA 1  103．（2022·重庆市实验中学高二期末）已知A2,0 ､ B8,0 ､C4,2 ，且动点 满足 PB 2，则 P 2 PC  PB P 取得最小值时，点 的坐标是___________.   71, 71 【答案】 PA  2 x22y2 1     【解析】设 Px,y，则  PB   x82y2 4，整理可得： x2y2 16 ； 2 PC  PB 2 PC 2 PA 2PC  PA  ，  A,P,C P AC 2 PC  PB 当 三点共线且 在线段 上时， 取得最小值， y2 x4  又直线 方程为： ，即 ， AC 02 24 yx2 x2y2 16  x 71  x1 7    由 得： 或 ， yx2 y 71 y1 7   P 71, 71 又P在线段AC上， .   71, 71 故答案为： . x2y22x6y0 E0,1 l l 104．（2022·江苏江苏·高二期中）在圆 内，过点 互相垂直的两条直线 1， 2与 圆分别相交于点A，C和B，D，则四边形ABCD的面积的最大值为_______. 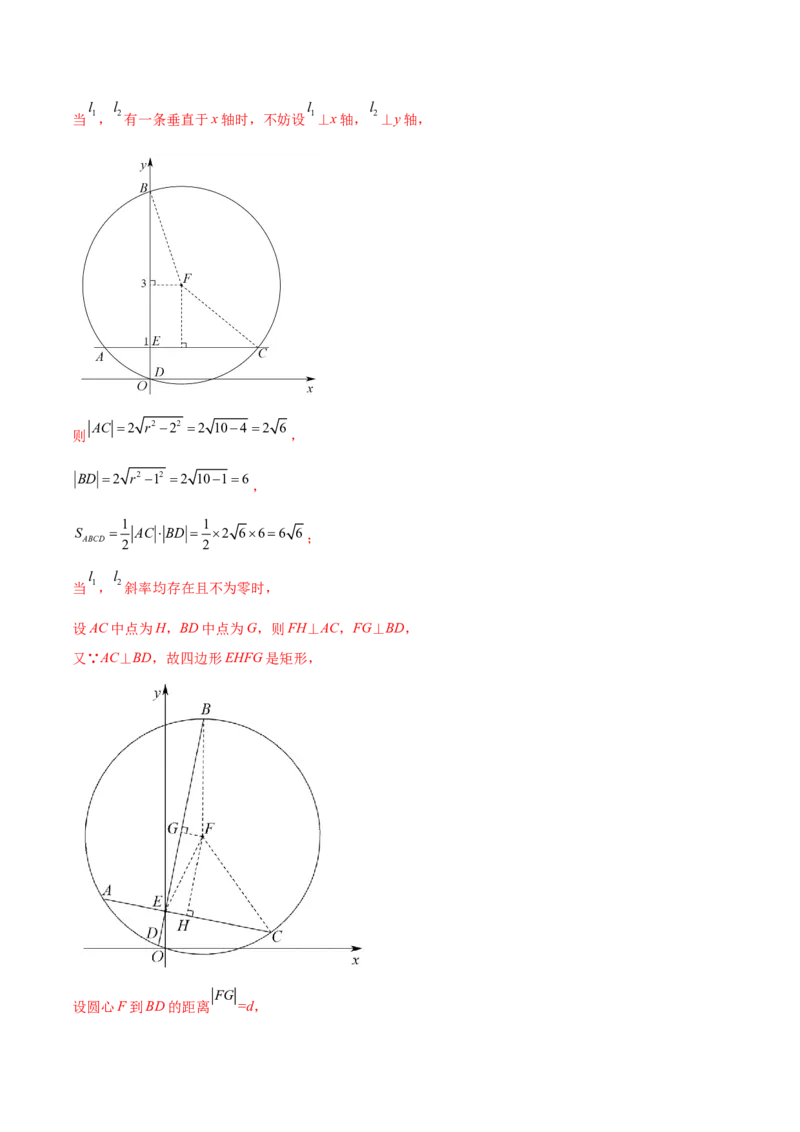【答案】15 x2y22x6y0(x1)2(y3)2 10 【解析】由 ， 10 设圆心为F(1，3)，半径r= ，l l l l 当 1， 2有一条垂直于x轴时，不妨设 1⊥x轴， 2⊥y轴， AC 2 r222 2 104 2 6 则 ， BD 2 r212 2 1016 ， 1 1 S  AC  BD  2 666 6； ABCD 2 2 l l 当 1， 2斜率均存在且不为零时， 设AC中点为H，BD中点为G，则FH⊥AC，FG⊥BD， 又∵AC⊥BD，故四边形EHFG是矩形， FG 设圆心F到BD的距离 =d，BD 2 r2d2 2 10d2 则 ， FH |2 EG|2 EF|2  FG|25d2 ， AC 2 r2|FH |2 2 105d2 2 5d2 ， 1 5d210d2  2 S ABCD  2 AC  BD 2  5d2 10d2 2   2   15 ，当且仅当 5d2 10d2 ，即 10 d  时取等号； 2 6 6 15  ，∴四边形ABCD面积的最大值为15﹒ 故答案为：15． x32y32 4 105．（多选题）（2022·江苏·南京市秦淮中学高二期末）已知动点P在圆 上，点 A2,0 B0,1 、 ，则（ ） A．点P到直线AB的距离小于6 B．点P到直线AB的距离大于2 PB 3 PB 3 PBA PBA C．当 最小时， D．当 最大时， 【答案】ACD A2,0 B0,1 【解析】因为点 、 ，所以过A、B的直线方程为即x+2y-2=0. x32y32 4 圆 的圆心坐标为(3,3)，半径r=2. 362 7 5 d   因为圆心到直线x+2y-2=0的距离 1222 5 ，  7 5 7 5  2 , 2 所以点P到直线AB的距离的范围为 5 5 .   点P到直线AB的距离小于6,但不一定大于2故A正确,B错误. 如图,当过B的直线与圆相切时,满足∠PBA最小或最大(P点位于P 时∠PBA最小,位于P 时∠PBA最大),此时 1 2 BC  3222  13 , PB BC2r2  134 3 所以 ,故C、D正确. 故选：ACD M:x12y12 4 l:x y20 P 106．（多选题）（2022·广东东莞·高二期末）已知圆 ，直线 ， 为直 线l上的动点，过点P作圆M 的切线PA、PB，切点为A、B，则下列结论正确的是（ ） A．四边形MAPB面积的最小值为4 B．四边形MAPB面积的最大值为8 PA 2 2 C．当APB最大时， D．当APB最大时，直线AB的方程为xy0 【答案】AD 【解析】如下图所示：由圆的几何性质可得MAPA，MBPB， PA  PB MA  MB MP  MP △PAM≌△PBM 由切线长定理可得 ，又因为 ， ，所以， ， S 2S  PA AM 2 PA 所以， 四边形MAPB △PAM ， PA  MP2 MA2  MP2 4 MP 因为 ，当MPl时， 取最小值， 112 MP  2 2  2 2 2 2 4 4 且 min 2 ，所以，四边形MAPB的面积的最小值为 ，A对； MP PA MAPB 因为 无最大值，即 无最大值，故四边形 面积无最大值，B错； AM 2 sinAPM   因为 APM 为锐角， APB2APM ，且 MP MP ， MP PA 2 APM APB 故当 最小时， 最大，此时 最大，此时 ，C错； PA  PB  MA  MB 2 APB PAM 90 由上可知，当 最大时， 且 ， 故四边形MAPB为正方形，且有MPl，则MP的方程为 yx ， yx x1   联立xy20，可得y1，即点P1,1 ， O0,0 yx AB MP AB 由正方形的几何性质可知，直线 过线段 的中点 ，此时直线 的方程为 ，D对. 故选：AD. C:x2y26x0 l:mx4ym40(mR) 107．（多选题）（2022·浙江浙江·高二期中）已知圆 ，直线 ， 则下列结论正确的有（ ） A．圆C的圆心坐标为(3,0)，半径为9 (1,1) B．对于任意实数m直线l恒过定点 C．若直线l交圆C于A，B两点，则弦长AB的最小值为4 m3 △ABD 5 5 D．当 时，直线l交圆C于A，B两点，D是圆C上的动点，则 面积的最大值为 【答案】BCDC:x2y26x0 C:x32y2 9 (3,0) 【解析】对于A选项，圆 化为标准方程得圆 ，故圆C的圆心坐标为 ， 半径为3，故A选项错误； l:mx14y40(mR) l x10 y10 对于B选项，由题知直线 ，所以直线 过直线 与直线 的交点， l E(1,1) 所以直线 过定点 ，故B正确； E(1,1) C l CE AB 对于C选项，由于点 在圆 内，故当直线 与直线 垂直时，弦 取得最小值，此时最小弦长为 2 9CE2 2 9CE2 4 ，故C正确； m3 l:3x4y10 (3,0) l:3x4y10 对于D选项，当 时，直线 ，此时圆心 到直线 的距离为 10 1 d   2，弦长 AB 2 94 2 5，所以 面积的最大值为 2 5325 5，故D正确. 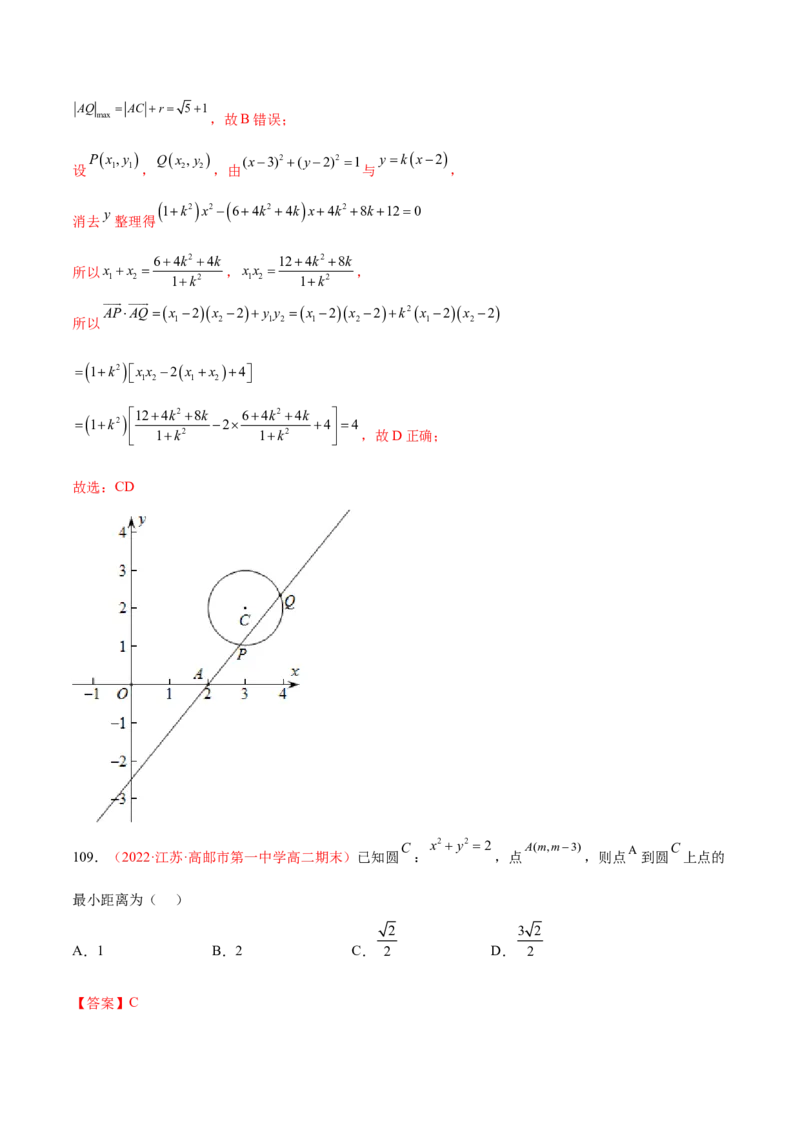5 △ABD 2 故选：BCD C:(x3)2(y2)2 1 A(2,0) 108．（多选题）（2022·重庆市实验中学高二期末）已知圆 ，点 ，过点A的 直线与圆C交于两点P，Q，且APAQ．则（ ） A．直线PQ的斜率k�1 B．AQ的最小值为2   AP 51 APAQ4 C． 的最小值为 D． 【答案】CD C:(x3)2(y2)2 1 C3,2 r1 【解析】依题意圆 的圆心坐标为 ，半径 ， 显然直线AP的斜率存在，设斜率为 k ，则直线 AP:ykx2 ，即 kxy2k 0 ， 3k22k d  1 3 所以 k212 ，解得k  ，故A错误； 4 因为 AC  322202  5 ，所以 AP  AC r  51，故C正确； min 当直线与圆相切时，AP AQ，又APAQ，所以AQ不存在最小值，只存在最大值且 AQ  AC r 51 maxAQ  AC r 51 max ，故B错误； Px,y  Qx ,y  (x3)2(y2)2 1 ykx2 设 1 1 ， 2 2 ，由 与 ， y  1k2 x2  64k24k  x4k28k120 消去 整理得 64k24k 124k28k 所以x x  ，xx  ， 1 2 1k2 1 2 1k2   APAQx 2x 2y y x 2x 2k2x 2x 2 所以 1 2 1 2 1 2 1 2   1k2 xx 2x x 4  1 2 1 2  124k28k 64k24k    1k2  2 44  1k2 1k2  ，故D正确； 故选：CD C x2y2 2 A(m,m3) A C 109．（2022·江苏·高邮市第一中学高二期末）已知圆 ： ，点 ，则点 到圆 上点的 最小距离为（ ） 2 3 2 A．1 B．2 C． 2 D． 2 【答案】C【解析】由圆 C ： x2y2 2 ，得圆 C0,0 ，半径r为 2 ， AC  m2m32  2m26m9 所以  32 9 3 2  2 m   ， 2 2 2 3 2 2  2  所以点A到圆C上点的最小距离为 2 2 . 故选：C. C:x2y24x4y80 l:2xy80 110．（2022·河北邯郸·高二期末）已知圆 ，直线 ，P为直线l上的 动点，过点P作圆C的切线，切点分别为点A，B，圆C的圆心为C，当四边形PACB的面积最小时， AB  （ ） 2 5 4 5 6 5 8 5 A． 5 B． 5 C． 5 D． 5 【答案】D x22y22 16 C2,2 【解析】圆C化为 ，∴圆心为 ，半径为4. PA PACB △PAC 若使四边形 的面积最小，则需使 的面积最小，即 最小， 2228 PC  PA2 AC2 d  2 5 ∴ 最小，即求C到直线l的距离， 5 ， PC 2 5 PA 2 此时 ， ， 1 1  1  AB  PC   PA AC ， 2 2  2 24 8 5 AB 2  ∴ 2 5 5 . 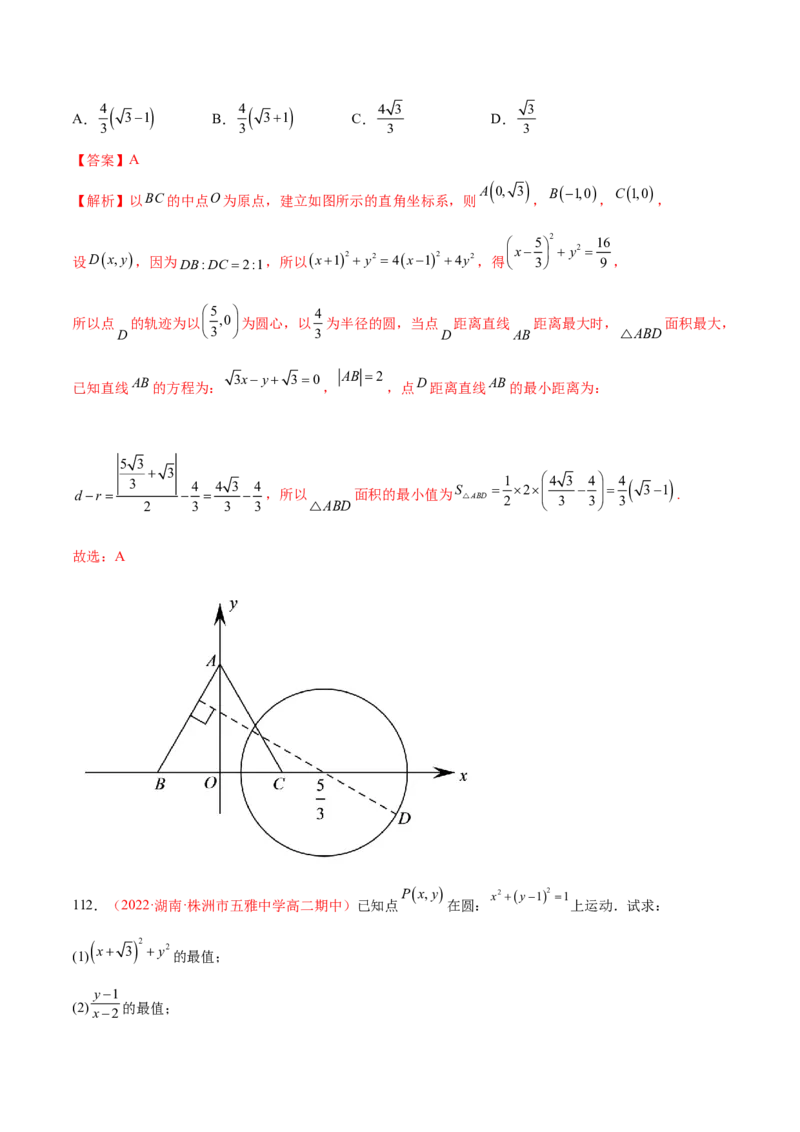故选：D 111．（2022·江西抚州·高二期末（理））已知边长为2的等边三角形ABC，D是平面ABC内一点，且满 足DB:DC 2:1，则三角形ABD面积的最小值是（ ）4  4  4 3 3 A． 31 B． 31 C． D． 3 3 3 3 【答案】A   A 0, 3 B1,0 C1,0 【解析】以BC的中点O为原点，建立如图所示的直角坐标系，则 ， ， ，  5 2 16 设Dx,y ，因为DB:DC 2:1，所以x12y2 4x124y2，得   x 3   y2  9 ， 5  4 所以点 的轨迹为以 ,0为圆心，以 为半径的圆，当点 距离直线 距离最大时， 面积最大， D 3  3 D AB △ABD AB 3xy 30 AB 2 D AB 已知直线 的方程为： ， ，点 距离直线 的最小距离为： 5 3  3 dr  3  4  4 3  4 ，所以 面积的最小值为 S △ABD  1 2 2    4 3 3  4 3     4 3  31  . 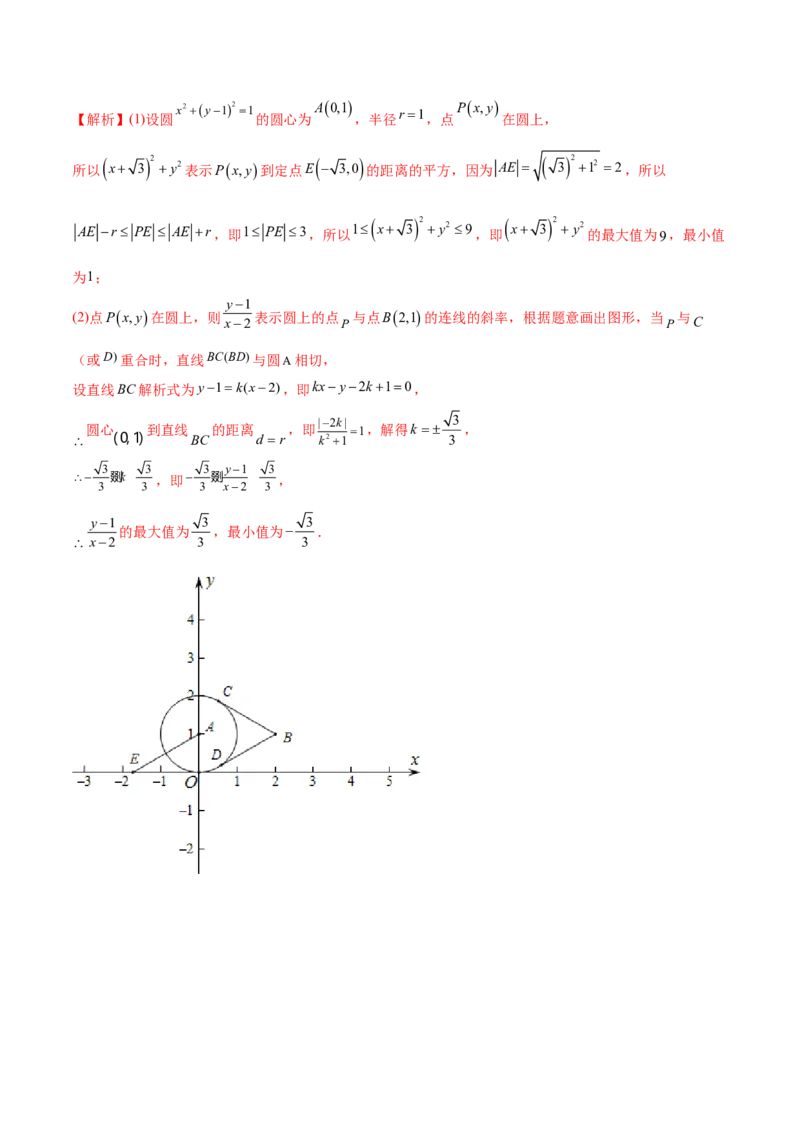2 3 3 3 △ABD   故选：A Px,y x2y12 1 112．（2022·湖南·株洲市五雅中学高二期中）已知点 在圆： 上运动．试求：  2 x 3 y2 (1) 的最值； y1 (2) 的最值； x2x2y12 1 A0,1 r1 Px,y 【解析】(1)设圆 的圆心为 ，半径 ，点 在圆上， 所以  x 3 2 y2表示Px,y到定点E   3,0  的距离的平方，因为 AE   3 2 12 2，所以  2  2 AE r PE  AE r，即1 PE 3，所以 1 x 3 y2 9 ，即 x 3 y2 的最大值为9，最小值 为1； y1 (2)点Px,y在圆上，则 表示圆上的点 与点B2,1的连线的斜率，根据题意画出图形，当 与 x2 P P C （或D)重合时，直线BC(BD)与圆A相切， 设直线BC解析式为y1k(x2)，即kxy2k10， |2k| 3 圆心 到直线 的距离 ，即 1，解得k  ，  (0,1) BC d r k21 3 3 3 3 y1 3  剟k ，即 剟 ， 3 3 3 x2 3 y1 3 3 的最大值为 ，最小值为 ．  x2 3 3