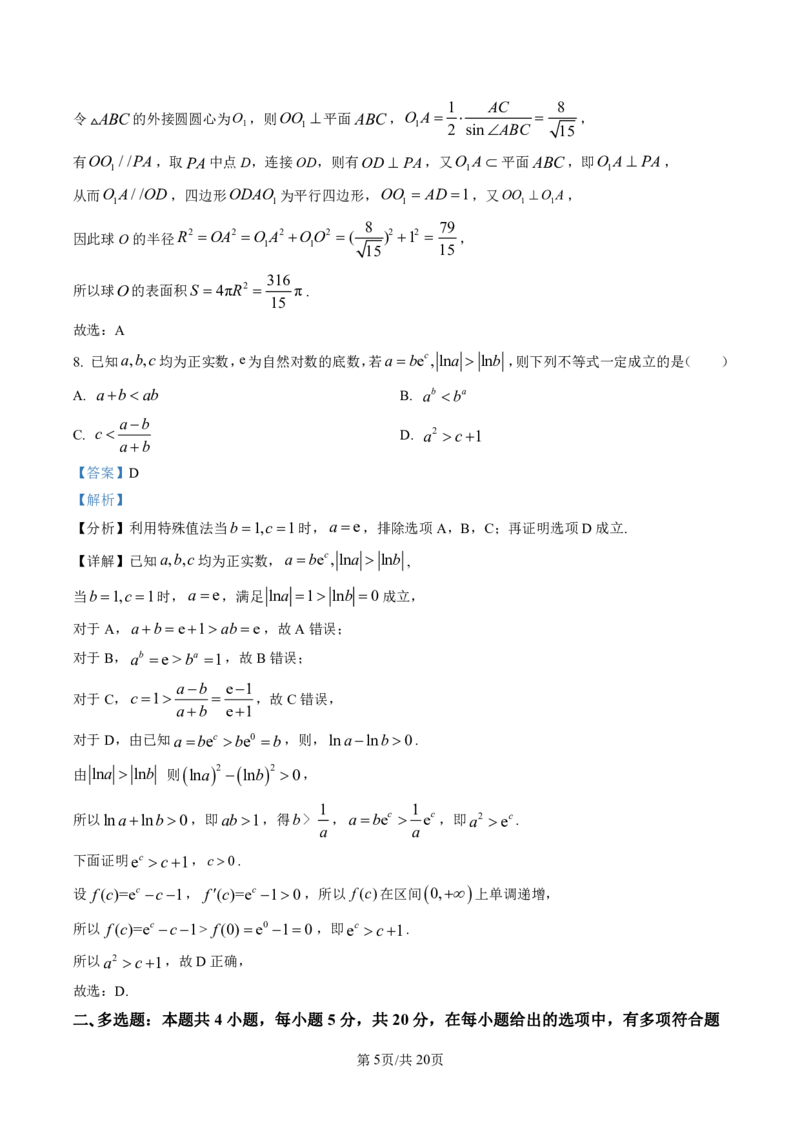广东省广州市2023届高三综合测试（一）数学试题（解析版）_2024年2月_01每日更新_13号_2023届广州市普通高中毕业班综合测试(一)全科_2023年广州市普通高中毕业班综合测试(一)数学

秘密 启用前 试卷类型：A ★ 2023 年广州市普通高中毕业班综合测试（一） 数学 本试卷共 5页､22小题､满分 150分､考试用时 120分钟. 注意事项： 1.答卷前､考生务必川黑色字迹的钢笔或签字色将自己的姓名､考生号､试室号､座位号填写在 答题卡上.用 2B铅笔将试卷类型（A）填涂在答题卡的相应位置上，并在答题卡相应位置上填 涂考生号. 2.作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑； 如需改动，用橡皮擦下净后，再选涂其他答案，答案不能答在试卷上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相 应位置上：如需改动，先划掉原来的答案，然后再写上新答案：不准使用铅笔和涂改液.不按 以上要求作答无效. 4.考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回. 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. z  1. 若复数z 34i，则 z （ ） 3 4 3 4 3 4 3 4 A.  i B.  i C.   i D.   i 5 5 5 5 5 5 5 5 【答案】A 【解析】 【分析】根据给定条件，求出复数z的共轭复数及模，即可计算作答. 【详解】复数z 34i，则z 34i，|z| 32 (4)2 5， z 3 4 所以   i . z 5 5 故选：A 2. 已知集合A  xZ∣x22x30  ，则集合A的子集个数为（ ） A.3 B.4 C.8 D.16 【答案】C 第1页/共20页 学科网（北京）股份有限公司【解析】 【分析】解一元二次不等式，并结合已知用列举法表示集合A作答. 【详解】解不等式x2 2x30，得1 x3，因此A xZ∣1 x3 {0,1,2}， 所以集合A的子集个数为23 8. 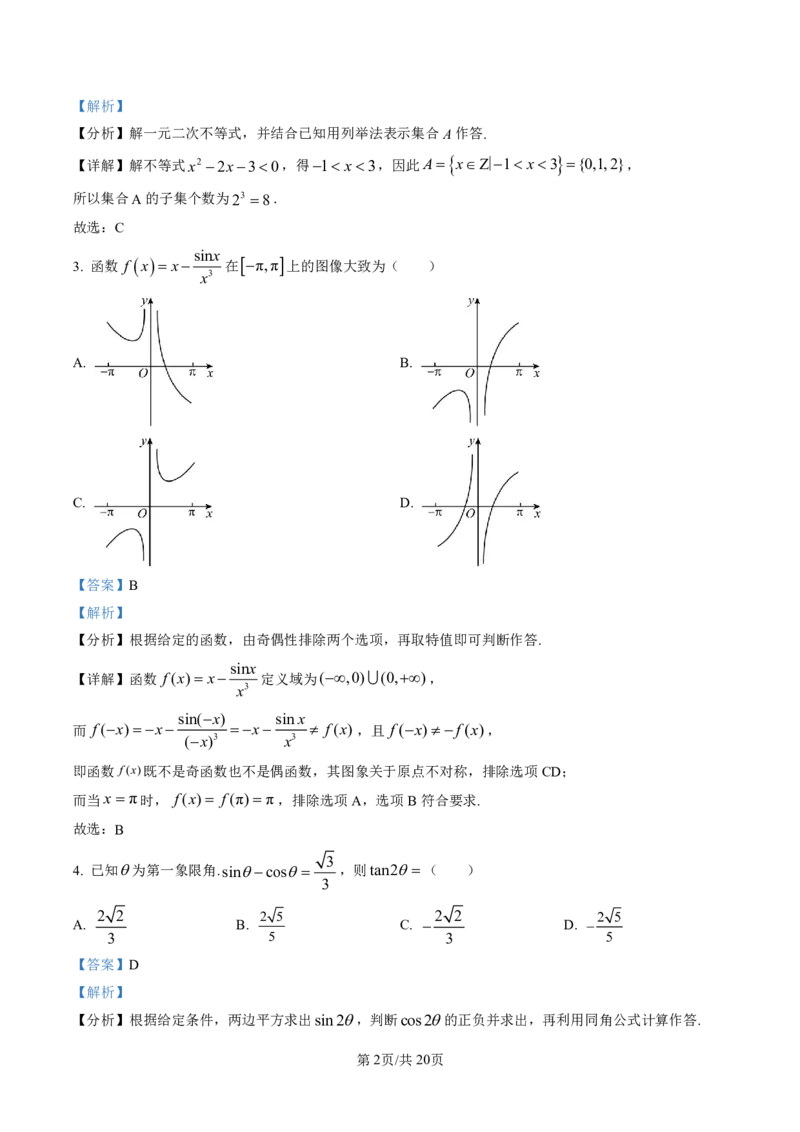故选：C sinx 3. 函数 f  x  x 在 π,π  上的图像大致为（ ） x3 A. B. C. D. 【答案】B 【解析】 【分析】根据给定的函数，由奇偶性排除两个选项，再取特值即可判断作答. sinx 【详解】函数 f(x) x 定义域为(,0)(0,)， x3 sin(x) sinx 而 f(x)x x  f(x) ，且 f(x)f(x)， (x)3 x3 即函数 f(x)既不是奇函数也不是偶函数，其图象关于原点不对称，排除选项CD； 而当x π时， f(x) f(π) π，排除选项A，选项B符合要求. 故选：B 3 4. 已知为第一象限角.sincos ，则tan2（ ） 3 2 2 2 5 2 2 2 5 A. B. C.  D.  3 5 3 5 【答案】D 【解析】 【分析】根据给定条件，两边平方求出sin2，判断cos2的正负并求出，再利用同角公式计算作答. 第2页/共20页 学科网（北京）股份有限公司3 【详解】因为为第一象限角，sincos 0 ，则sincos0，cos2cos2sin20， 3 1 1 2 5 (sincos)2  ，即1sin2 ，解得sin2 ，cos2 1sin22 ， 3 3 3 3 sin2 2 5 所以tan2  . cos2 5 故选：D 5.“回文”是古今中外都有的一种修辞手法，如“我为人人，人人为我”等，数学上具有这样特征的一类数称为 “回文数”､“回文数”是指从左到右与从右到左读都一样的正整数，如121，241142等，在所有五位正整数中， 有且仅有两位数字是奇数的“回文数”共有（ ） A.100个 B.125个 C.225个 D.250个 【答案】C 【解析】 【分析】根据给定的信息，确定五位正整数中的“回文数”特征，再由0出现的次数分类求解作答. 【详解】依题意，五位正整数中的“回文数”具有：万位与个位数字相同，且不能为0；千位与十位数字相同， 求有且仅有两位数字是奇数的“回文数”的个数有两类办法： 最多1个0，取奇数字有A1种，取能重复的偶数字有A1 种，它们排入数位有A2种，取偶数字占百位有A1 5 4 2 5 种， 不同“回文数”的个数是A1A1A2A1 200个， 5 4 2 5 最少2个0，取奇数字有A1种，占万位和个位，两个0占位有1种，取偶数字占百位有A1种， 5 5 不同“回文数”的个数是A1A1 25个， 5 5 由分类加法计算原理知，在所有五位正整数中，有且仅有两位数字是奇数的“回文数”共有20025 225个. 故选：C 6. 已知抛物线C的顶点为坐标原点O，焦点F 任x铀上，过点  2,0  的且线交C于P,Q两点，且OP OQ， 线段PQ的中点为M ，则直线MF的斜率的取大值为（ ） 6 1 2 A. B. C. D.1 6 2 2 【答案】A 【解析】 【分析】根据给定条件，设出抛物线C及直线PQ的方程，借助垂直关系求出抛物线方程及点M的坐标， 再用斜率坐标公式建立函数，利用均值不等式求解作答. 【详解】依题意，抛物线C的焦点在x轴的正半轴上，设C的方程为： y2  2px,p  0， 第3页/共20页 学科网（北京）股份有限公司y2 y2 显然直线PQ不垂直于y轴，设直线PQ的方程为：x  ty  2，点P( 1 ,y ),Q( 2 ,y )， 2p 1 2p 2 xty2 由 消去x得： y2 2pty4p2 0，则有y y 4p2， y2 2px 1 2   y2 y2 由OP OQ得：OPOQ  1  2  y y  44p 0，解得 p 1， 2p 2p 1 2 1 2pt 于是抛物线C：y2 2x的焦点F( ,0)，弦PQ的中点M 的纵坐标为 t，则点M(t2 2,t)， 2 2 t 2 2 6 k     显然直线MF的斜率最大，必有t 0，则直线MF的斜率 t2  3 2t 3 2 2t 3 6 ， 2 t t 3 6 当且仅当2t  ，即t  时取等号， t 2 6 所以直线MF的斜率的取大值为 . 6 故选：A 7. 已知三棱锥PABC的四个顶点都在球O的球面上，PB  PC 2 5,AB  AC 4，PABC 2， 则球O的表面积为（ ） 316 79 158 79 A. π B. π C. π D. π 15 15 5 5 【答案】A 【解析】 【分析】根据给定条件，证明PA平面ABC，再确定球心O的位置，求出球半径作答. 【详解】在三棱锥PABC中，如图，AB2 PA2 20 PB2，则PA AB，同理PA AC， 而ABAC  A,AB,AC 平面ABC，因此PA平面ABC， 1 BC 15 在等腰ABC中，AB AC4,BC2，则 2 1，sinABC  1cos2ABC  ， cosABC   4 AB 4 第4页/共20页 学科网（北京）股份有限公司1 AC 8 令ABC的外接圆圆心为O ，则OO 平面ABC，O A   ， 1 1 1 2 sinABC 15 有OO //PA，取PA中点D，连接OD，则有OD  PA，又O A 平面ABC，即O A PA， 1 1 1 从而O A//OD，四边形ODAO 为平行四边形，OO  AD 1，又OO O A， 1 1 1 1 1 8 79 因此球O的半径R2 OA2 O A2 OO2  ( )2 12  ， 1 1 15 15 316 所以球O的表面积S 4πR2  π. 15 故选：A 8. 已知a,b,c均为正实数，e为自然对数的底数，若a bec, lna  lnb ，则下列不等式一定成立的是（ ） A. abab B. ab ba ab C. c D. a2 c1 ab 【答案】D 【解析】 【分析】利用特殊值法当b1,c 1时，ae，排除选项A，B，C；再证明选项D成立. 【详解】已知a,b,c均为正实数，a bec, lna  lnb , 当b1,c 1时，ae，满足 lna 1 lnb 0成立， 对于A，abe1abe，故A错误； 对于B，ab e>ba 1，故B错误； ab e1 对于C，c1  ，故C错误， ab e1 对于D，由已知abec be0 b，则，lnalnb0. 由 lna  lnb 则 lna 2  lnb 2 0， 1 1 所以lnalnb0，即ab1，得b> ，abec  ec，即a2 ec. a a 下面证明ec c1，c0. 设 f(c)=ec c1， f(c)=ec 10，所以 f(c)在区间  0, 上单调递增， 所以 f(c)=ec c1> f(0)e0 10，即ec c1. 所以a2 c1，故D正确， 故选：D. 二､多选题：本题共 4小题，每小题 5分，共 20分，在每小题给出的选项中，有多项符合题 第5页/共20页 学科网（北京）股份有限公司目要求.全部选对的得5分，部分选对的得 2分，有选错的得 0分. 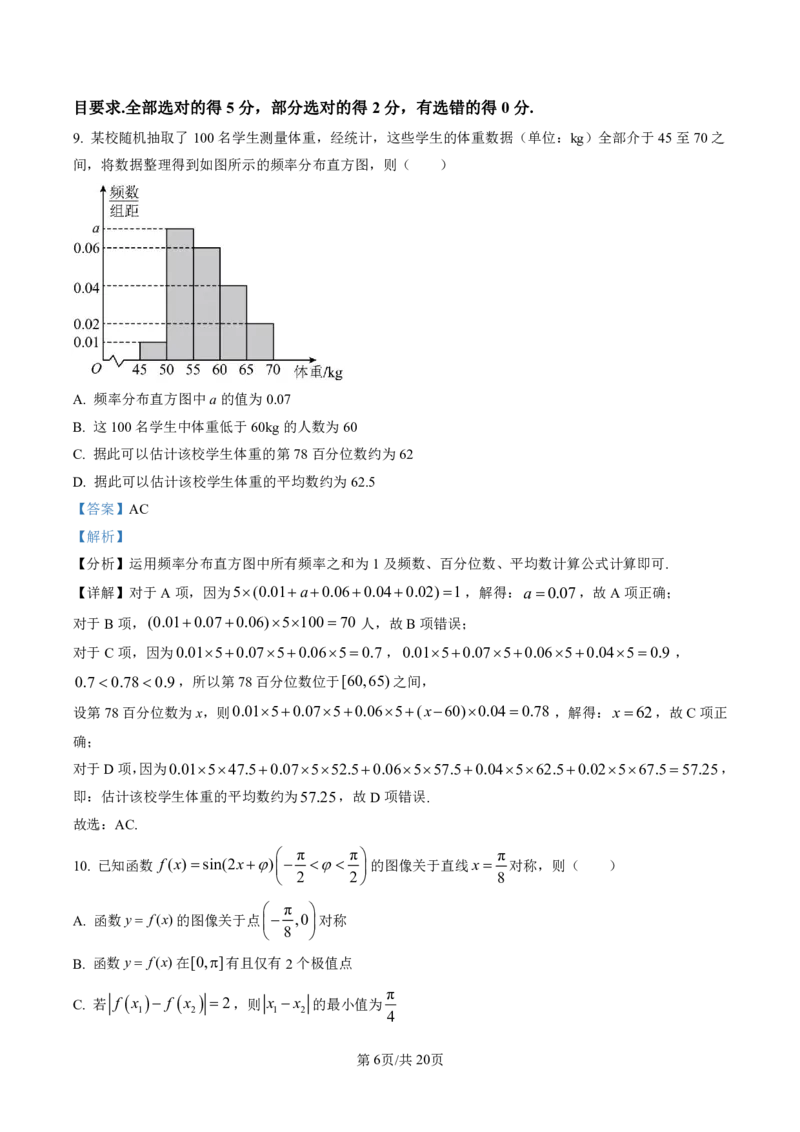9. 某校随机抽取了100名学生测量体重，经统计，这些学生的体重数据（单位：kg）全部介于45至70之 间，将数据整理得到如图所示的频率分布直方图，则（ ） A. 频率分布直方图中a的值为0.07 B. 这100名学生中体重低于60kg的人数为60 C. 据此可以估计该校学生体重的第78百分位数约为62 D. 据此可以估计该校学生体重的平均数约为62.5 【答案】AC 【解析】 【分析】运用频率分布直方图中所有频率之和为1及频数、百分位数、平均数计算公式计算即可. 【详解】对于A项，因为5(0.01a0.060.040.02)1，解得：a0.07，故A项正确； 对于B项，(0.010.070.06)510070 人，故B项错误； 对于C项，因为0.0150.0750.0650.7 ，0.0150.0750.0650.0450.9 ， 0.70.780.9，所以第78百分位数位于[60,65)之间， 设第78百分位数为x，则0.0150.0750.065(x60)0.040.78 ，解得：x62，故C项正 确； 对于D项，因为0.01547.50.07552.50.06557.50.04562.50.02567.557.25， 即：估计该校学生体重的平均数约为57.25，故D项错误. 故选：AC.  π π π 10. 已知函数 f(x)sin(2x)   的图像关于直线x 对称，则（ ）  2 2 8  π  A. 函数y f(x)的图像关于点  ,0对称  8  B. 函数y f(x)在[0,]有且仅有2个极值点 π C. 若 f  x  f  x   2，则 x x 的最小值为 1 2 1 2 4 第6页/共20页 学科网（北京）股份有限公司 π  π 1 D. 若 f    f     ，则cos2 1cos2   8  8 2 【答案】ABD 【解析】 【分析】利用函数图象的对称性求出，再结合正弦函数的图象与性质逐项分析、计算判断作答. π π π π π π 【详解】依题意，2 kπ ,kZ，即kπ ,kZ，而  ，则 ， 8 2 4 2 2 4 π f(x)sin(2x )， 4 π π π π 对于A，因为 f( )sin[2( ) ]0，于是函数y f(x)的图像关于点( ,0)对称，A正确； 8 8 4 8 π π 9π π 9π 对于B，当x[0,π]时， 2x  ，而正弦函数y sinx在[ , ]上有且只有两个极值点， 4 4 4 4 4 所以函数y f(x)在[0,]有且仅有2个极值点，B正确； 对于C，因为 f(x) 1, f(x) 1，又 f  x  f  x   2，因此x,x 中一个为函数 f(x)的最大值点， max min 1 2 1 2 2π π 另一个为其最小值点，又函数 f(x)的周期为 π，所以 x x 的最小值为 ，C错误； 2 1 2 2 π π 1 对于D，依题意， f( )f( )sin2sin2 ， 8 8 2 则cos2 cos2  (cos2cos2sin2sin2)(cos2cos2sin2sin2 ) 2sin2sin21，因此cos2 1cos2  ，D正确. 故选：ABD 11. 已知函数 f  x  x2 2  x0  ,g  x aex(a 0)，点P,Q分別在函数 y f  x  的y  g  x  的图 像上，O为坐标原点，则下列命题正确的是（ ） A. 若关于x的方程 f  x g  x 0在  0,1  上无解，则a 3e B. 存在P,Q关于直线 y  x对称 C. 若存在P,Q关于y轴对称，则0 a  2 1 D. 若存在P,Q满足POQ90，则0a 2 2e 【答案】BCD 【解析】 【分析】根据给定条件，求出方程 f  x g  x 0在  0,1  上有解的a范围判断A；设出点P,Q的坐标， 由方程有解判断B；设出点P,Q的坐标，建立函数关系，求出函数的值域判断CD作答. 第7页/共20页 学科网（北京）股份有限公司【详解】函数 f  x  x2 2  x0  ,g  x aex(a 0) ， 对于A，方程 f  x g  x 0h(x) x2 2aex 0在  0,1  上有解， h(0)2a0   显然函数h(x)在 0,1 上单调递增，则有 ，解得2a3e， h(1)3ae1 0 因此关于x的方程 f  x g  x 0在  0,1  上无解，则0a2或a 3e，A错误； 对于B，设点Q(t,aet)，依题意，点Q关于直线 y x对称点(aet,t)在函数 f  x  x2 2的图象上， 即关于t的方程t a2e2t 2有解，即a2 (t2)e2t有解，此时t 2，令函数(t)(t2)e2t,t  2， (t)(2t3)e2t  0，即函数(t)在(2,)上单调递增，(t)(2)0， 而函数 y t2,y e2t在(2,)上都单调递增，它们的取值集合分别为(0,),(e4,)， 因此函数(t)的值域为(0,)，又a2 0，于是a2 (t2)e2t在(2,)有解， 所以存在P,Q关于直线 y x对称，B正确； 对于C，设点P(u,u2 2),u 0，则点P关于y轴对称点(u,u2 2)在函数g(x)aex(a 0)的图象上， u2 2 u2 2 u2 2u2 (u1)2 1 即aeu u2 2 a ，令F(u) ,u 0 ，F(u)  0， eu eu eu eu 即函数F(u)在[0,)上单调递减，F(u)  F(0)2，又u[0,)，恒有F(u)0，因此0 a  2， max C正确；   对于D，令P(x ,x2 2),Q(x ,aex 2)，由POQ90得OPOQ  x x aex 2(x22) 0， 1 1 2 1 2 1 x x x 1x 显然x x 0，且x 0,x 0，a 1  2 ，令G(x) ,x0，G(x) ， 1 2 1 2 x2 2 ex 2 ex ex 1 当0 x 1时G(x)0，函数G(x)单调递增，当x1时，G(x)0，函数G(x)单调递减， 1 1 x 1 因此G(x) G(1) ，即有0G(x) ，0 2  ， max e e ex 2 e x x 1 x x 1 而0 1  1  ，当且仅当x  2时取等号，所以0 1  2  ，即 x2 2 2 2x2 2 2 2 x2 2 ex 2 2 2e 1 1 1 1 0a ，D正确. 2 2e 故选：BCD 12. 平面内到两定点距离之积为常数的点的轨迹称为卡西尼卵形线，它是1675年卡西尼在研究土星及其卫 星的运行规律时发现的，已知在平面直角坐标系xOy中，M(2,0)，N(2,0)，动点P满足|PM ||PN |5， 则下列结论正确的是（ ） 第8页/共20页 学科网（北京）股份有限公司A. 点P的横坐标的取值范围是   5, 5    B. OP 的取值范围是 1,3 5 C. PMN面积的最大值为 2 D. PM  PN 的取值范围是   2 5,5  【答案】BC 【解析】 【分析】设出点P的坐标，列出方程并化简整理，放缩解不等式判断A；利用几何意义并结合求函数值域 判断B；利用三角形面积公式计算判断C；取点计算判断D作答. 【详解】设点P(x,y)，依题意，[(x2)2  y2][(x2)2  y2]25， 对于A，25[(x2)2  y2][(x2)2  y2](x2)2(x2)2 (x2 4)2，当且仅当y0时取等号， 解不等式(x2 4)2 25得：3≤x≤3，即点P的横坐标的取值范围是[3,3]，A错误； 对于B，[(x2  y2 4)4x][(x2  y2 4)4x]25，则x2  y2 4 2516x2 ， 显然0 x2 9，因此 |OP| x2 y2  2516x2 4[1,3] ，B正确； 1 1 5 对于C，PMN的面积S  |PM ||PN |sinMPN  |PM ||PN | ，当且仅当MPN 90时取 2 2 2 等号，  x2  y2 4 当MPN 90时，点P在以线段MN为直径的圆x2  y2 4上，由 解得 x2  y2 4 2516x2  39 x   4  ，  5 y   4 5 所以PMN面积的最大值为 ，C正确； 2 对于D，因为点(3,0)在动点P的轨迹上，当点P为此点时， PM  PN 516，D错误. 故选：BC 【点睛】易错点睛：求解轨迹方程问题，设出动点坐标，根据条件求列出方程，再化简整理求解，还应特 别注意：补上在轨迹上而坐标不是方程解的点，剔出不在轨迹上而坐标是方程解的点. 三､填空题：本题共 4小题，每小题 5分，共 20分. 第9页/共20页 学科网（北京）股份有限公司r r      13. 已知向量a  1,2  ,b 3,x  ,a 与ab共线，则 ab  __________. 【答案】2 5. 【解析】 【分析】运用平面向量共线及向量的模的坐标计算公式求解即可.   【详解】由题意知，ab(4,2x)    又因为a//(ab)，所以1(2 x)24，所以x6，    所以b(3,6)，所以ab(2,4)，   所以|ab| (2)2 (4)2 2 5. 故答案为：2 5. 14. 已知nN，将数列2n1与数列  n2 1  的公共项从小到大排列得到新数列  a  ，则 n 1 1 1    __________. a a a 1 2 10 10 【答案】 21 【解析】 【分析】分析可知2n1是正奇数列，根据题意求得 a 4n2 1，然后利用裂项相消法可求得 n 1 1 1   的值. a a a 1 2 10 【详解】因为数列2n1是正奇数列， 对于数列  n2 1  ，当n为奇数时，设n2k1  kN ，则n2 1 2k1 2 14k  k1 为偶数； 当n为偶数时，设n2k  kN ，则n2 14k2 1为奇数， 1 1 1 1  1 1  所以，a 4n2 1，则      ， n a 4n2 1  2n1  2n1  2 2n1 2n1 n 1 1 1 1  1 1 1 1 1  1  1  10 因此，    1       1   . a a a 2 3 3 5 19 21 2 21 21 1 2 10 10 故答案为： . 21 15. 已知函数 f(x)的定义域为(0,)，其导函数为 f(x)，若xf(x)10. f(e)2，则关于x的不等式 f(ex) x1的解集为__________. 【答案】(1,) 第10页/共20页 学科网（北京）股份有限公司【解析】 【分析】根据给定条件，构造函数g(x) f(x)lnx,x0，再利用函数探讨单调性，求解不等式作答. 1 xf(x)1 【详解】令函数g(x) f(x)lnx,x0，则g(x) f(x)  0 ，因此函数g(x)在(0,) x x 上单调递减， g(e) f(e)lne1，因此 f(ex) x1 f(ex)x1 g(ex) g(e)，即ex e，解得x1， 所以不等式 f(ex) x1的解集为(1,). 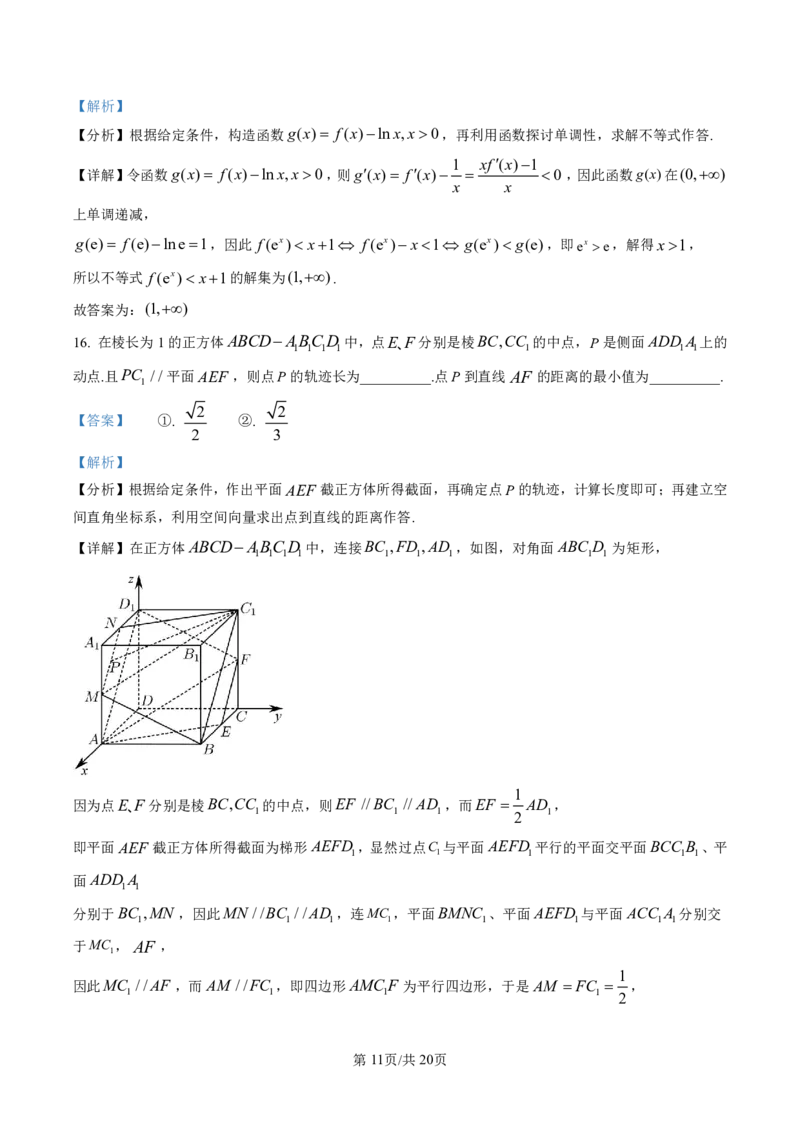故答案为：(1,) 16. 在棱长为1的正方体ABCDABCD 中，点E､F分别是棱BC,CC 的中点，P是侧面ADD A上的 1 1 1 1 1 1 1 动点.且PC //平面AEF ，则点P的轨迹长为__________.点P到直线 AF 的距离的最小值为__________. 1 2 2 【答案】 ①. ②. 2 3 【解析】 【分析】根据给定条件，作出平面AEF 截正方体所得截面，再确定点P的轨迹，计算长度即可；再建立空 间直角坐标系，利用空间向量求出点到直线的距离作答. 【详解】在正方体ABCDABCD 中，连接BC ,FD ,AD ，如图，对角面ABC D 为矩形， 1 1 1 1 1 1 1 1 1 1 因为点E､F分别是棱BC,CC 的中点，则EF //BC //AD ，而EF  AD ， 1 1 1 2 1 即平面AEF 截正方体所得截面为梯形AEFD ，显然过点C 与平面AEFD 平行的平面交平面BCC B 、平 1 1 1 1 1 面ADD A 1 1 分别于BC ,MN ，因此MN //BC //AD ，连MC ，平面BMNC 、平面AEFD 与平面ACC A 分别交 1 1 1 1 1 1 1 1 于MC ， AF ， 1 1 因此MC //AF ，而AM //FC ，即四边形AMCF 为平行四边形，于是AM  FC  ， 1 1 1 1 2 第11页/共20页 学科网（北京）股份有限公司2 即点M为AA 的中点，同理N 为AD 中点，MN  ，因为动点P始终满足PC //平面AEF ， 1 1 1 1 2 2 于是PC 平面BMNC ，又P在侧面ADD A上，所以点P的轨迹是线段MN，轨迹长为 ； 1 1 1 1 2 1 1 1 以点D为原点建立空间直角坐标系，则M(1,0, ),N( ,0,1),A(1,0,0),F(0,1, )， 2 2 2  1 1  1  1   1 1 则MN ( ,0, ),AM (0,0, ),AF (1,1, )，令MP tMN ( t,0, t)， 2 2 2 2 2 2 13t      1 1t   13t APAF 4 1 1 则有AP  AM MP  ( t,0, )，APAF  ,    t ， 2 2 4 | AF | 3 2 6 2 于是点P到直线 AF 的距离    APAF 1 1 1 1 1 1 2 2 d  |AP|2 (  )2  t2 (t1)2( t )2  t2 t  ， | AF | 4 4 2 6 4 3 9 3 2 当且仅当t 0时取等号，所以点P到直线 AF 的距离的最小值为 . 3 2 2 故答案为： ； 2 3 【点睛】方法点睛：作截面的常用三种方法：直接法，截面的定点在几何体的棱上；平行线法，截面与几 何体的两个平行平面相交，或者截面上有一条直线与几何体的某个面平行；延长交线得交点，截面上的点 中至少有两个点在几何体的同一平面上. 四､解答题：本题共 6小题，共 70分，解答应写出文字说明.证明过程或演算步骤. 17. 已知数列  a  的前n项和为S ，且S 2n 2a 1 n n n n a  （1）求a ，并证明数列 n 是等差数列： 1 2n （2）若2a2  S ，求正整数k的所有取值. k 2k 【答案】（1）a 1，证明见解析 1 （2）1,2,3 【解析】 S ,n1 a a 【分析】（1）根据a  1 证明 n  n1 为定值即可； n S S ,n2 2n 2n1 n n1 （2）先根据（1）求出a ，再利用错位相减法求出S ，从而可得2a2,S ，再根据函数的单调性即可得解. n n k 2k 第12页/共20页 学科网（北京）股份有限公司【小问1详解】 由S 2n 2a 1，得S 2a 2n 1， n n n n 当n 1时，S a 2a 21，所以a 1， 1 1 1 1 当n2时，S 2a 2n11， n1 n1 两式相减得a 2a a 2n1，即a a 2n1， n n n1 n n1 a a 1 所以 n  n1  ， 2n 2n1 2 a  a 1 所以数列 n 是以 1  为首项， 1 为公差的等差数列； 2n 2 2 2 【小问2详解】 a n 由（1）得 n  ，所以a n2n1， 2n 2 n S 122322 n2n1， n 2S 2222 323 n2n， n 12n 两式相减得S 1222232n1n2n n2n  1n  2n1 ， n 12 所以S  n1  2n 1， n 则S  2k1  22k 1,2a2 k222k1， 2k k 由2a2  S ， k 2k 得k222k1  2k1  22k 1， 1 即k2 4k2 0， 22k1 1 令 f  x  x2 4x2 ， 22x1 1 因为函数 y  x2 4x2,y  在2,上都是增函数， 22x1 1 所以函数 f  x  x2 4x2 在2,上是增函数， 22x1 1 3 1 17 由 f  1 142  0, f  2 482  0， 2 2 8 8 1 1 1 1 f  3 9122 1 0, f  4 16162 2 0， 25 25 27 27 第13页/共20页 学科网（北京）股份有限公司则当x4时， f  x 0， 所以若2a2  S ，正整数k的所有取值为1,2,3. k 2k C A 3 18. 记ABC的内角A、B、C的对边分别为a、b、c.已知acos2 ccos2  b . 2 2 2 （1）证明：sinAsinC 2sinB； uuur uuur （2）若b2， ABAC 3 ，求ABC的面积. 【答案】（1）证明见解析 3 5 （2）S  △ABC 4 【解析】 【分析】（1）利用三角恒等变换结合正弦定理化简可证得结论成立； （2）利用平面向量数量积的定义可得出bccosA3，结合余弦定理以及ac2b4可求得a、c的值， 由此可求得ABC的面积. 【小问1详解】 C A 3 a  1cosC c  1cosA  3 因为acos2 ccos2  b ，则  b， 2 2 2 2 2 即acacosCccosA3b， 由正弦定理可得3sinB sin AsinC sin AcosCcosAsinC sin AsinCsin  AC  sin AsinCsin  πB sin AsinCsinB， 因此，sinAsinC 2sinB. 【小问2详解】 因为sinAsinC 2sinB，由正弦定理可得ac2b4，   由平面向量数量积的定义可得ABAC cbcosA3， b2 c2 a2 4c2 a2 所以，2c  3，可得c2 a2  2， 2bc 2 1 9 7 即  ca  ca  4  ca  2，所以，ca  ，则c ，a  ， 2 4 4 3 3 2 cosA   2 2 5 所以， bc 2 9 3，则A为锐角，且sin A 1cos2 A  1    ， 3 3 4 1 1 1 9 5 3 5 因此，S  bcsinA  2   . △ABC 2 2 2 4 3 4 19. 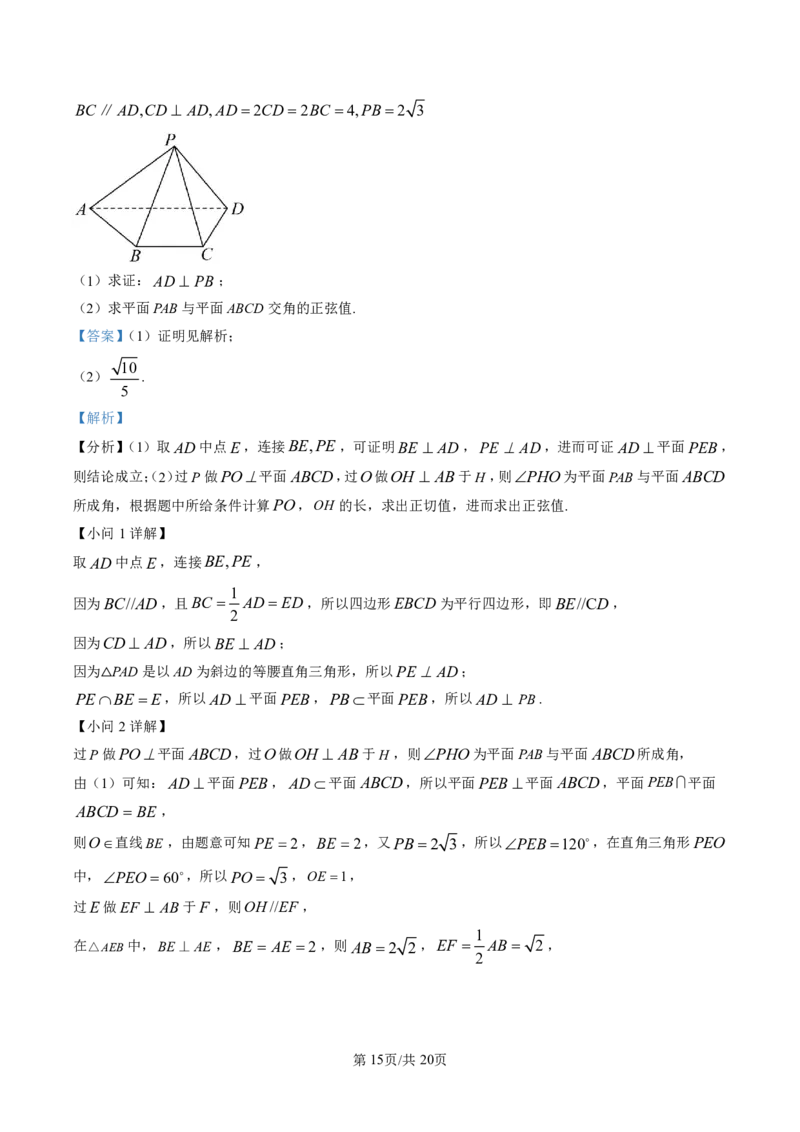如图，在四棱锥P-ABCD中， PAD是以AD为斜边的等腰直角三角形， △ 第14页/共20页 学科网（北京）股份有限公司BC∥AD,CD  AD,AD 2CD 2BC 4,PB 2 3 （1）求证：AD  PB； （2）求平面PAB与平面ABCD交角的正弦值. 【答案】（1）证明见解析； 10 （2） . 5 【解析】 【分析】（1）取AD中点E，连接BE,PE，可证明BE  AD，PEAD，进而可证AD 平面PEB， 则结论成立；（2）过P做PO平面ABCD，过O做OH  AB于H ，则PHO为平面PAB与平面ABCD 所成角，根据题中所给条件计算PO，OH 的长，求出正切值，进而求出正弦值. 【小问1详解】 取AD中点E，连接BE,PE， 1 因为BC//AD，且BC  AD  ED，所以四边形EBCD为平行四边形，即BE//CD， 2 因为CD AD，所以BE  AD； 因为 PAD是以AD为斜边的等腰直角三角形，所以PEAD； PE △BE  E，所以AD 平面PEB，PB平面PEB，所以AD  PB. 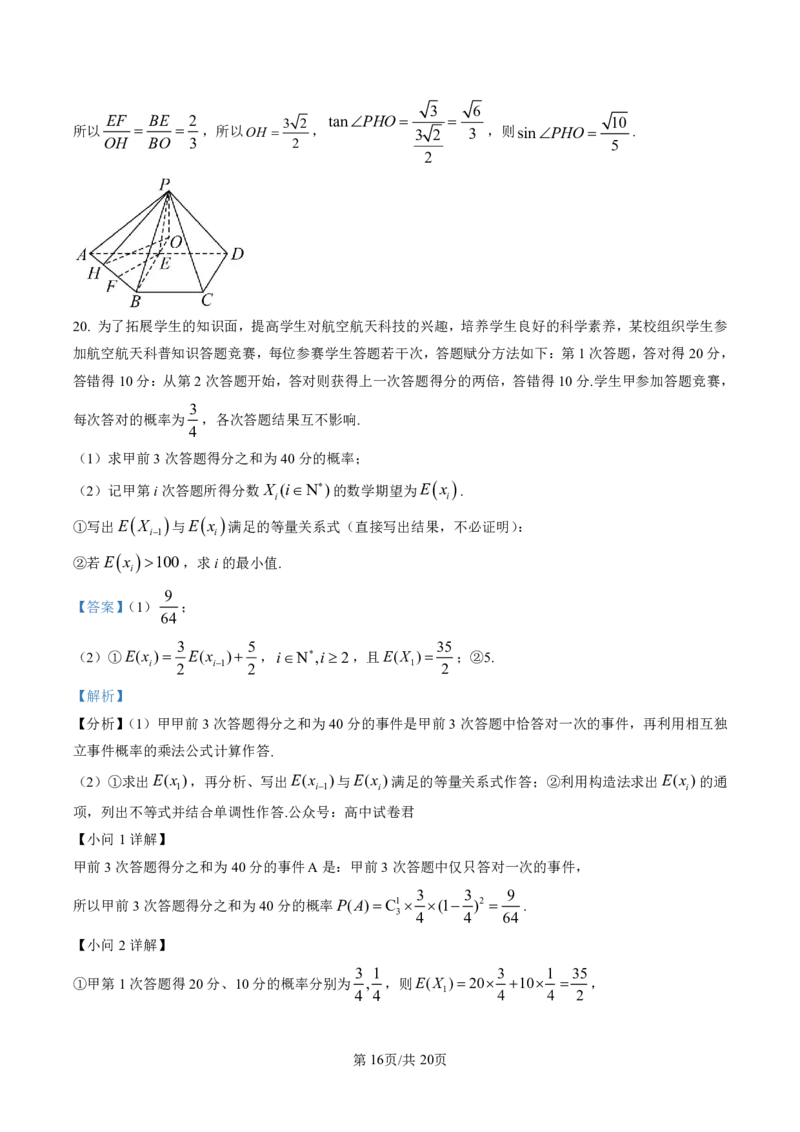【小问2详解】 过P做PO平面ABCD，过O做OH  AB于H ，则PHO为平面PAB与平面ABCD所成角， 由（1）可知：AD 平面PEB，AD 平面ABCD，所以平面PEB 平面ABCD，平面PEB平面 ABCD  BE， 则O直线BE ，由题意可知PE 2，BE 2，又PB2 3，所以PEB 120，在直角三角形PEO 中，PEO 60，所以PO  3，OE 1， 过E做EF  AB于F ，则OH//EF ， 1 在△AEB中，BE⊥AE ，BE  AE 2，则AB2 2，EF  AB  2， 2 第15页/共20页 学科网（北京）股份有限公司3 6 EF BE 2 3 2 tanPHO  10 所以   ，所以OH  ， 3 2 3 ，则sinPHO  . OH BO 3 2 5 2 20. 为了拓展学生的知识面，提高学生对航空航天科技的兴趣，培养学生良好的科学素养，某校组织学生参 加航空航天科普知识答题竞赛，每位参赛学生答题若干次，答题赋分方法如下：第1次答题，答对得20分， 答错得10分：从第2次答题开始，答对则获得上一次答题得分的两倍，答错得10分.学生甲参加答题竞赛， 3 每次答对的概率为 ，各次答题结果互不影响. 4 （1）求甲前3次答题得分之和为40分的概率； （2）记甲第i次答题所得分数X (iN)的数学期望为E  x  . i i     ①写出E X 与E x 满足的等量关系式（直接写出结果，不必证明）： i1 i ②若E  x 100，求i的最小值. i 9 【答案】（1） ； 64 3 5 35 （2）①E(x ) E(x ) ，iN,i2，且E(X ) ；②5. i 2 i1 2 1 2 【解析】 【分析】（1）甲甲前3次答题得分之和为40分的事件是甲前3次答题中恰答对一次的事件，再利用相互独 立事件概率的乘法公式计算作答. （2）①求出E(x )，再分析、写出E(x )与E(x )满足的等量关系式作答；②利用构造法求出E(x )的通 1 i1 i i 项，列出不等式并结合单调性作答.公众号：高中试卷君 【小问1详解】 甲前3次答题得分之和为40分的事件A是：甲前3次答题中仅只答对一次的事件， 3 3 9 所以甲前3次答题得分之和为40分的概率P(A)C1 (1 )2  . 3 4 4 64 【小问2详解】 3 1 3 1 35 ①甲第1次答题得20分、10分的概率分别为 , ，则E(X )20 10  ， 4 4 1 4 4 2 第16页/共20页 学科网（北京）股份有限公司3 3 1 3 1 甲第2次答题得40分、20分、10分的概率分别为  ,  , ， 4 4 4 4 4 3 3 1 3 1 115 则E  X 40  20  10  ，显然 2 4 4 4 4 4 4 3 1 3 1 3 5 E(X )2(20 10 ) 10  E(X ) ， 2 4 4 4 4 2 1 2 iN,i2，甲第i1次答题所得分数X 的数学期望为E(x )， i1 i1 3 1 因此第i次答对题所得分数为2E(x )，答错题所得分数为10分，其概率分别为 , ， i1 4 4 3 1 3 5 于是甲第i次答题所得分数X 的数学期望为E(x )2E(x ) 10  E(x ) ， i i i1 4 4 2 i1 2 3 5 35 所以E(x )与E(x )满足的等量关系式是：E(x ) E(x ) ，iN,i2，且E(X ) ； i1 i i 2 i1 2 1 2 35 3 45 ②由①知，E(X ) ，当iN,i2时，E(x )5 [E(x )5]，而E(X )5 ， 1 2 i 2 i1 1 2 45 3 45 3 3 因此数列{E(x )5}以 为首项， 为公比的等比数列，E(x )5 ( )i1 15( )i， i 2 2 i 2 2 2 3 3 3 3 于是E(x )15( )i 5，由15( )i 5100得：( )i 7，显然数列{( )i}是递增数列， i 2 2 2 2 3 81 3 243 而( )4  7,( )5  7，则有正整数i 5， min 2 16 2 32 所以i的最小值是5. x2 y2 2 21. 已知椭圆C:  1(a b 0)的离心率为 ，以C的短轴为直径的圆与直线 yax6相切. a2 b2 2 （1）求C的方程； （2）直线l：y k(x1)(k 0)与C相交于A，B两点，过C上的点P作x轴的平行线交线段AB于点Q， 直线OP的斜率为k（O为坐标原点）， APQ的面积为S . VBPQ的面积为S ，若| AP|S |BP|S ， 1 2 2 1 判断kk是否为定值？并说明理由. △ x2 y2 【答案】（1）   1； 8 4 1 （2）是定值， . 2 【解析】 【分析】（1）利用椭圆离心率及圆的切线性质，建立关于a,b的方程组，解方程组作答. （2）由给定的面积关系可得直线PQ平分APB，进而可得直线AP,BP的斜率互为相反数，再联立直线 与椭圆方程，利用韦达定理结合斜率坐标公式计算判断作答. 第17页/共20页 学科网（北京）股份有限公司【小问1详解】 2 a2 b2 1 由椭圆C的离心率为 得：  ，即有a2 2b2， 2 a2 2 6 由以C的短轴为直径的圆与直线 yax6相切得： b，联立解得a2 8,b2 4， a2 1 x2 y2 所以C的方程是   1. 8 4 【小问2详解】 1 kk为定值，且kk ， 2 1 | AP||PQ|sinAPQ | AP| S 2 | AP|sinAPQ 因为| AP|S |BP|S ，则  1   ， 2 1 |BP| S 1 |BP|sinBPQ 2 |BP||PQ|sinBPQ 2 因此sinAPQsinBPQ，而APQBPQABP(0,π)，有APQ BPQ， 于是PQ平分APB，直线AP,BP的斜率k ,k 互为相反数，即k k 0， AP BP AP BP 设A(x ,y ),B(x ,y ),P(x ,y ) ， 1 1 2 2 0 0  4k2 x2 y2 x x    1  1 2 2k2 1 由 8 4 得，(2k2 1)x2 4k2x2k2 80，即有 ，   2k2 8 y k(x1) x x   1 2 2k2 1 y  y y  y 而k k  1 0  2 0 0，则(y  y )(x x ) y  y  (x x )0， AP BP x x x x 1 0 2 0 2 0 1 0 1 0 2 0 即[k(x 1) y ](x x )[k(x 1) y ](x x ) 2kx x (y kx k)(x x )2x (y k)0 1 0 2 0 2 0 1 0 1 2 0 0 1 2 0 0 2k2 8 4k2 于是2k (y kx k) 2x (y k)0 2k2 1 0 0 2k2 1 0 0  2k(2k2 8)4k2(y kx k)2x (y k)(2k2 1)0， 0 0 0 0 化简得：2y (x 1)k2 (x 8)kx y 0， 0 0 0 0 0 x 2 y 2 且又因为P(x ,y )在椭圆上，即 0  0 1，即x 2 2y 2 8，2y 2 x 2 x  x 8， 0 0 0 0 0 0 0 0 8 4 从而2y (x 1)k2 (2y 2 x 2 x )kx y 0，(2y k x )[(x 1)k  y ]0 ， 0 0 0 0 0 0 0 0 0 0 0 y 1 又因为P(x ,y )不在直线l: y k(x1)上，则有2y kx 0，即k 0 kk ， 0 0 0 0 x 2 0 第18页/共20页 学科网（北京）股份有限公司1 所以kk为定值，且kk . 2 【点睛】方法点睛：求定值问题常见的方法有两种：（1）从特殊入手，求出定值，再证明这个值与变量无 关．（2）直接推理、计算，并在计算推理的过程中消去变量，从而得到定值． 22. 已知a0，函数 f  x  1ax  ex1  . （1）若a 1，证明：当x0时， f  x ln  x1  ： （2）若函数h  x ln  x1  f  x  存在极小值点x ，证明： f  x 0 0 0 【答案】（1）证明见解析； （2）证明见解析. 【解析】 【分析】（1）把a 1代入，构造函数g(x)ln(x1)(1x)(ex 1),x0，借助导数确定单调性推理作 答. （2）由给定条件确定a的取值范围，再分段讨论函数h(x)的极小值点及极小值推理判断作答. 【小问1详解】 若a 1，则 f(x)(1x)(ex 1)，设g(x)ln(x1)(1x)(ex 1),x0， 1 x[(x1)ex 1] g(x) [(ex1)(1x)ex] ，设(x)(x1)ex 1,x0， x1 x1 (x)(x2)ex 0，则(x)在(0,)上单调递增，(x)(0)0，即g(x)0， 于是g(x)在(0,)上单调递增，g(x) g(0)0，即 f(x)ln(x1)， 所以当x0时， f(x)ln(x1). 【小问2详解】 函数h(x)ln(x1)(1ax)(ex 1),a 0，其定义域为(1,),h(0)0， 1 (x1)(axa1)ex  (axa1) (axa1)[(x1)ex 1] h(x) (axa1)ex a  ， x1 x1 x1 由（1）知(x)(x1)ex 1在(1,)上单调递增，(0)0， 当x(1,0)时，(x)0，当x(0,)时，(x) 0， 1 1 1 则由h(x)0，解得x0或x 1，其中 11且 10，即a0且a1， a a a 否则恒有h(x)0，则h(x)在(1,)上单调递增，函数h(x)无极值点，不符合题意， 1 1 若1 10，即a 1，当x(1, 1)(0,)时，h(x)0， a a 第19页/共20页 学科网（北京）股份有限公司1 1 当x( 1,0)时，h(x)0，则h(x) 在(1, 1),(0,)上单调递增， a a 1 在( 1,0)上单调递减，因此x0是h(x)的极小值点， f(0)0， a 1 1 若 10，即0a1，当x(1,0)( 1,)时，h(x)0， a a 1 1 当x(0, 1)时，h(x)0，则h(x)在(1,0),( 1,)上单调递增， a a 1 1 在(0, 1)单调递减，因此x 1是h(x)的极小值点， a a 1 1 1 1 1 f( 1)a(ea 1)，又0a1, 10，于是 f( 1)0， a a a 综上所述，函数h(x)ln(x1) f(x)存在极小值点x , f  x 0. 0 0 【点睛】思路点睛：函数不等式证明问题，将所证不等式等价转化，构造新函数，再借助函数的单调性、 极(最)值问题处理. 第20页/共20页 学科网（北京）股份有限公司