文档内容
格致课堂
第六章 综合检测题
一、选择题
1.向量 ( )
A. B. C. D.
【答案】A
【解析】向量 .
故选:A.
2.【2019年5月10日《每日一题》必修4向量数乘运算及其几何意义】
在四边形ABCD中, , , ,则四边形ABCD的形状是
A.长方形 B.平行四边形 C.菱形 D.梯形
【答案】D
【解析】由题意,因为 , , ,
∴ + + ,
∴AD∥BC,且AD≠BC,∴四边形ABCD为梯形,故选D.
3.在平面直角坐标系 中,已知四边形 是平行四边形, , ,则
( )
A. B. C. D.
【答案】D
【解析】因为四边形 是平行四边形,所以 ,所以
,故选D.
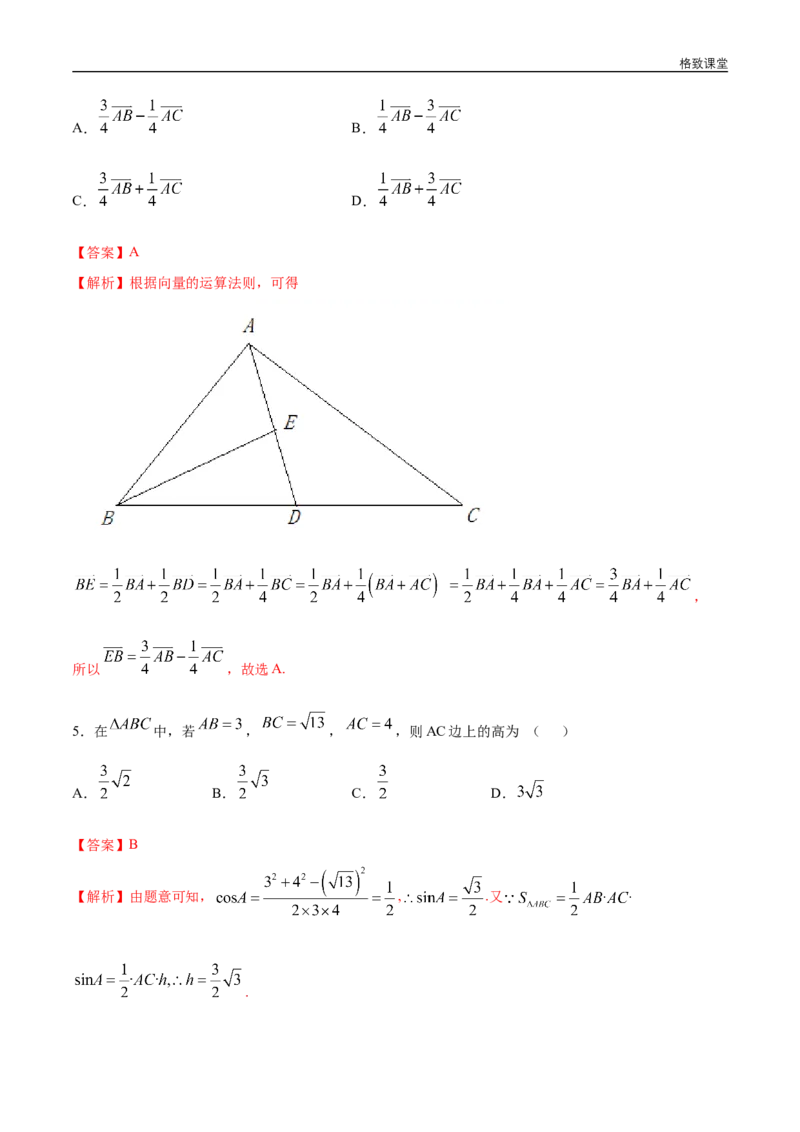
4.在△ 中, 为 边上的中线, 为 的中点,则格致课堂
A. B.
C. D.
【答案】A
【解析】根据向量的运算法则,可得
,
所以 ,故选A.
5.在 中,若 , , ,则AC边上的高为 ( )
A. B. C. D.
【答案】B
【解析】由题意可知, , .又
.格致课堂
故选B.
6.若平面向量 与 的夹角为 , , ,则向量 的模为( )
⃗a ⃗b 60° |⃗b|=4 (⃗a+2⃗b)•(⃗a-3⃗b)=-72 ⃗a
A.2 B.4 C.6 D.12
【答案】C
【解析】 , ,又 ,
∵(⃗a+2⃗b)·(⃗a-3⃗b)=-72 ∴|⃗a|2-⃗a·⃗b-6|⃗b|2=-72 ∵⃗a·⃗b=|⃗a|·|⃗b|cos60∘
∴|⃗a|2-2|⃗a|-24=0,则|⃗a|=6,故选C
7.如图,正方形 中, 是 的中点,若 ,则 ( )
A. B. C. D.
【答案】B
【解析】以 为坐标原点建立平面直角坐标系,设正方形边长为 ,
由此, ,故 ,
解得 .故选B.
8.已知向量 满足 , ,则
A.4 B.3 C.2 D.0
【答案】B
【解析】因为
所以选B.
9.(多选题)设a,b,c是任意的非零向量,且它们相互不共线,给出下列选项,其中正确的有( )
A.a·c-b·c=(a-b)·c; B.(b·c)·a-(c·a)·b不与c垂直;
C.|a|-|b|<|a-b|; D.(3a+2b)·(3a-2b)=9|a|2-4|b|2.格致课堂
【答案】A,C,D
【解析】根据向量积的分配律知A正确;因为[(b·c)·a-(c·a)·b]·c=(b·c)·(a·c)-(c·a)·(b·c)=0,∴(b·c)·a-
(c·a)·b与c垂直,B错误;因为a,b不共线,所以|a|,|b|,|a-b|组成三角形三边,∴|a|-|b|<|a-b|成立,
C正确;D正确.故正确命题的序号是A,C,D.
10.(多选题)给出下列四个命题,其中正确的选项有( )
A.非零向量a,b满足|a|=|b|=|a-b|,则a与a+b的夹角是30°
B.若(AB+AC)·(AB-AC)=0,则△ABC为等腰三角形
C.若单位向量a,b的夹角为120°,则当|2a+ |(x∈R)取最小值时x=1
D.若OA=(3,-4),OB=(6,-3),OC=(5-m,-3-m),∠ABC为锐角,则实数m的取值范围是m>
-.
【答案】A,B,C
【解析】A中,令OA=a,OB=b.以OA,OB为邻边作平行四边形OACB.∵|a|=|b|=|a-b|,
∴四边形OACB为菱形,∠AOB=60°,∠AOC=30°,即a与a+b的夹角是30°,故A正确.
B中,∵(AB+AC)·(AB-AC)=0,∴|AB|2=|AC|2,故△ABC为等腰三角形.故B正确.
C中,∵(2a+xb)2=4a2+4xa·b+x2b2=4+4xcos 120°+x2=x2-2x+4=(x-1)2+3,故|2a+xb|取最小值时x
=1.故③正确.
D中,∵BA=OA-OB=(3,-4)-(6,-3)=(-3,-1),BC=OC-OB=(5-m,-3-m)-(6,-3)=
(-1-m,-m),又∠ABC为锐角,∴BA·BC>0,即3+3m+m>0,∴m>-.又当BA与BC同向共线时,
m=,故当∠ABC为锐角时,m的取值范围是m>-且m≠.故D不正确.故选A,B,C.
11.(多选题)在△ABC中,角A,B,C所对的边分别为a,b,c,下列结论不正确的是( )
A.a2=b2+c2﹣2bccosA B .= C.a= D.
【答案】A,B,C
【解析】由在△ABC中,角A,B,C所对的边分别为a,b,c,知:
在A中,由余弦定理得:a2=b2+c2﹣2bccosA,故A正确;格致课堂
在B中,由正弦定理得: ,∴asinB=bsinA,故B正确;
在C中,∵a= ,∴由余弦定理得:a=b× +c× ,
整理,得2a2=2a2,故C正确;
在 D 中,由余弦定理得 acosB+bcosA=a× +b× = + =
c≠sinC,
故D错误.故选A,B,C.
12.(多选题)在△ABC中,根据下列条件解三角形,其中有一解的是( )
A.b=7,c=3,C=30° B.b=5,c=4,B=45°
C.a=6,b=3 ,B=60° D.a=20,b=30,A=30°
【解析】B,C
【解析】对于A,∵b=7,c=3,C=30°,
∴由正弦定理可得:sinB= = = >1,无解;
对于B,b=5,c=4,B=45°,
∴由正弦定理可得sinC= = = <1,且c<b,有一解;
对于C,∵a=6,b=3 ,B=60°,
∴由正弦定理可得:sinA= = =1,A=90°,此时C=30°,有一解;
对于D,∵a=20,b=30,A=30°,
∴由正弦定理可得:sinB= = = <1,且b>a,
∴B有两个可能值,本选项符合题意.故选B,C.
二、填空题
13.【贵州省贵阳市第一中学2020届高三上学期第三次月考数学(理)试题】格致课堂
已知 , ,则 ________.
【答案】
【解析】 , ,所以 ,
所以 ,所以 .
故答案为: .
14.在 中,角 所对的边分别为 .若 ,,则角
的大小为____________________.
【答案】
【解析】由 得 ,所以
由正弦定理 得 ,所以A= 或 (舍去)、
15.如图,在 中, , 是边 上一点, ,则
.格致课堂
【答案】
【解析】由图及题意得 , =
∴ =( )( )= +
= = .
16.设 , 是两个不共线的向量, =3 +4 , = -2 .若以 , 为基底表示向量 +2 ,即 +2
λ μ
=λ +μ ,则 = , = 。
1
−
【答案】 , 5
【解析】
,解得
三、解答题
17.【北京市海淀区清华大学附属中学2019-2020学年高二上学期期中数学试题】
在 中, .
(1)求 的值;
(2)若 ,求 以及 的值.
【答案】(1) ;(2)7, .格致课堂
【解析】(1)由余弦定理及已知得: .
(2)因为 为三角形内角,
所以 , ,
由正弦定理得: ,
又∵ .
,解得 ( 舍).
.
18.在平面直角坐标系中,已知 , , .
(1) 的值.
(2) 的余弦值.
√5
−
【答案】(1) ;(2) 5 .
【解析】(1) ,所以 .
(2)由(1)得 ,
所以 ,
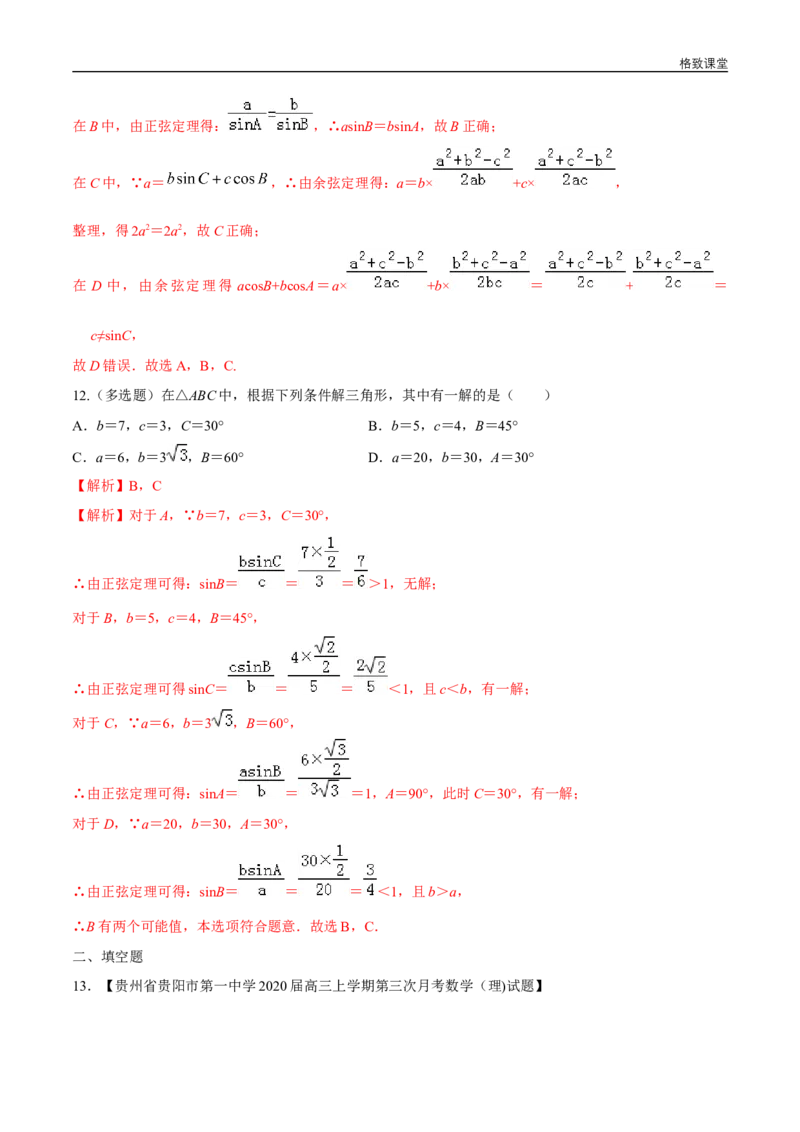
19.如图,渔船甲位于岛屿 的南偏西 方向的 处,且与岛屿 相距 ,渔船乙以格致课堂
的速度从岛屿 出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东 的方向追赶渔船乙,刚好用
追上.
(1)求渔船甲的速度;
(2)求 的值.
【答案】(1) ;(2) .
【解析】(1)依题意,知 , , , .
在 中,由余弦定理,得
,解得 ,
所以渔船甲的速度为 ;
(2)在 中, , , , ,
由正弦定理,得 ,即 .
20.在▱ABCD中,点M是AB的中点,点N在BD上,且BN= BD,求证:M,N,C三点共线.格致课堂
【答案】见解析
【解析】
= - .
因为 = , = = ( + ),
所以 = + - ,
= - .
由于 = - = - ,
可知 =3 ,即 ∥ .
又因为MC、MN有公共点M,所以M、N、C三点共线
21.已知 ,当 为何值时, 平行时它们是同向还是反向?
【答案】见解析
【解析】因为 ,
当 时,
则 ,解得:
此时 ,
= =格致课堂
= .
所以 反向.
22.在△ABC中,a=3,b=2 ,B=2A.
(1)求cos A的值;
(2)求c的值.
【答案】(1) ;(2) .
【解析】(1)因为a=3,b=2 ,∠B=2∠A,
所以在△ABC中,由正弦定理得 = .
所以 = .故cos A= .
(2)由(1)知cos A= ,所以sin A= = .
又因为∠B=2∠A,所以cos B=2cos2A-1= .
所以sin B= = .
在△ABC中,sin C=sin(A+B)=sin Acos B+
cos Asin B= .
所以c= =5.格致课堂