文档内容
4.2.1 指数函数的概念
4.2.2 指数函数的图象和性质
第 1 课时 指数函数的概念及其图象和性质
(教师独具内容)
课程标准:1.了解引入指数函数的背景,理解指数函数的概念和意义.2.能借
助计算器或计算机画出具体指数函数的图象.3.探索并理解指数函数的单调性、定
义域和值域及图象与参数的关系.
教学重点:1.理解指数函数的概念.2.借助指数函数的图象掌握指数函数的性
质,在“制图与识图”过程中体会数形结合思想.3.指数函数性质的一些简单应用.
教学难点:1.指数函数的图象与性质.2.底数a对函数的影响.
【知识导学】
知识点一 指数函数的定义
□函数y=ax(a>0,且a≠1)叫做指数函数,其中指数x是自变量,定义域是
R.
知识点二 指数增长模型
在实际问题中,经常会遇到指数增长模型:设原有量为N,每次的增长率为
p,经过x次增长,该量增长到y,则y=□N(1+p)x(x∈N).形如y=kax(k∈R,
且k≠0;a>0,且a≠1)的函数是刻画指数增长或指数衰减变化规律的非常有用的
函数模型.
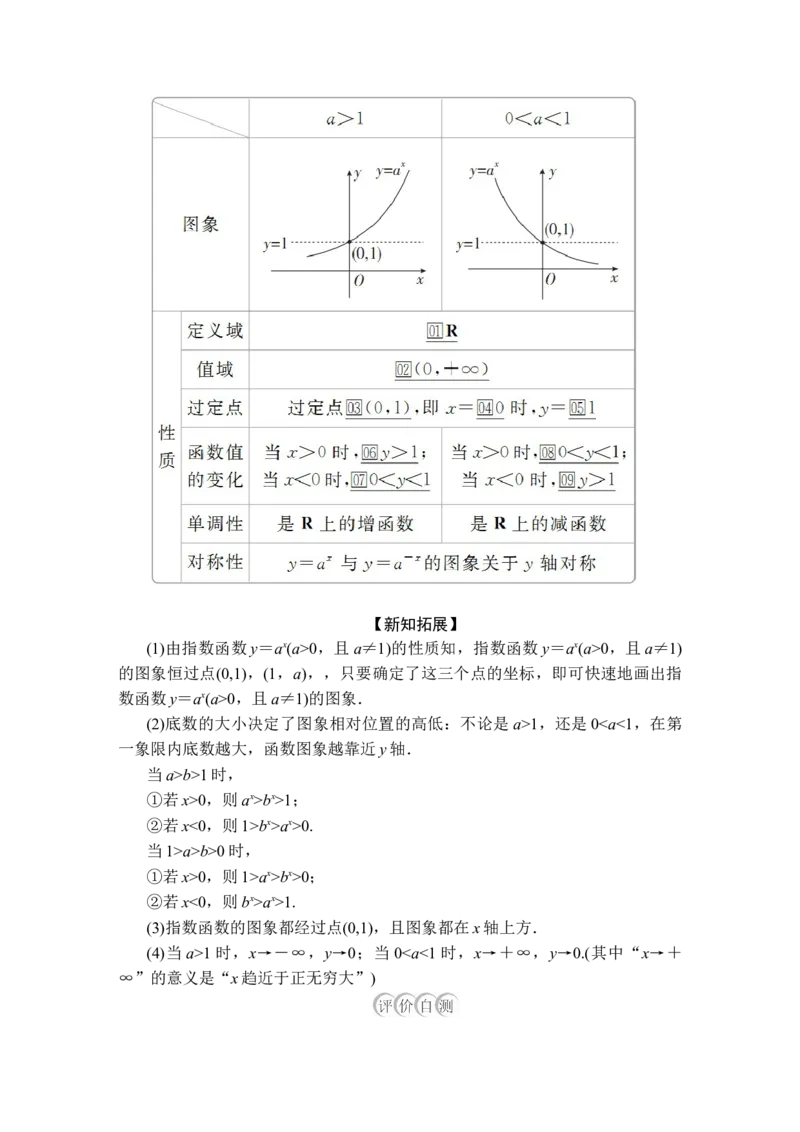
知识点三 指数函数的图象和性质【新知拓展】
(1)由指数函数y=ax(a>0,且a≠1)的性质知,指数函数y=ax(a>0,且a≠1)
的图象恒过点(0,1),(1,a),,只要确定了这三个点的坐标,即可快速地画出指
数函数y=ax(a>0,且a≠1)的图象.
(2)底数的大小决定了图象相对位置的高低:不论是a>1,还是0b>1时,
①若x>0,则ax>bx>1;
②若x<0,则1>bx>ax>0.
当1>a>b>0时,
①若x>0,则1>ax>bx>0;
②若x<0,则bx>ax>1.
(3)指数函数的图象都经过点(0,1),且图象都在x轴上方.
(4)当 a>1 时,x→-∞,y→0;当 01时,对于任意x∈R总有ax>1.( )
(3)函数f(x)=2-x在R上是增函数.( )
答案 (1)√ (2)× (3)×
2.做一做(请把正确的答案写在横线上)
(1)若f(x)=(a2-3)ax是指数函数,则a=________.
(2)若函数f(x)=ax(a>0,且a≠1)的图象过点(2,9),则f(x)=________.
(3)函数y=2的定义域为________,值域为________.
答案 (1)2 (2)3x (3)(-∞,0] [1,2)
题型一 指数函数的概念
例1 指出下列哪些是指数函数.
(1)y=4x;(2)y=x4;(3)y=-4x;(4)y=(-4)x;
(5)y=πx;(6)y=4x2;(7)y=xx;(8)y=(2a-1)x.
[解] (2)是四次函数;(3)是-1与4x的乘积;(4)中底数-4<0;(6)是二次函
数;(7)中底数x不是常数.它们都不符合指数函数的定义,故不是指数函数.
综上可知,(1)(5)(8)是指数函数.
金版点睛
判断一个函数是否为指数函数,只需判断其解析式是否符合 y=axa>0,且
a≠1这一形式即可.若符合,则函数为指数函数;否则就不是指数函数.
若函数y=(a2-3a+3)ax是指数函数,则a=________.
答案 2
解析 因为函数y=(a2-3a+3)ax是指数函数,
所以解得所以a=2.
题型二 指数函数的图象问题
例2 (1)如图是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图象,则
a,b,c,d与1的大小关系为( )A.a0,且a≠1)的图象过定点________.
[解析] (1)解法一:由图象可知③④的底数必大于1,①②的底数必小于1.
作直线x=1,在第一象限内直线x=1与各曲线的交点的纵坐标即各指数函
数的底数,则 10,且a≠1)的图象过定点(0,1),所以在函
数y=ax-3+3中,令x=3,得y=1+3=4,即函数的图象过定点(3,4).
解法二:将原函数变形,得 y-3=ax-3,把y-3看成x-3的指数函数,所
以当x-3=0时,y-3=1,即x=3时,y=4,所以原函数的图象过定点(3,4).
[答案] (1)B (2)(3,4)
金版点睛
1.识别指数函数图象问题的注意点
(1)根据图象“上升”或“下降”确定底数a>1或00,且a≠1)的图象过定点(0,1),据此,可解决形如y=k·ax
+c+b(k≠0,a>0,且a≠1)的函数图象过定点的问题,即令 x=-c,得y=k+
b,函数图象过定点(-c,k+b).(1)二次函数y=ax2+bx与指数函数y=x的图象可能是( )
(2)函数y=a2x+1+1(a>0,且a≠1)的图象过定点________.
答案 (1)A (2)
解析 (1)二次函数 y=a2-,其图象的顶点坐标为,由指数函数的图象知
0<<1,所以-<-<0,再观察四个选项,只有A中的抛物线的顶点的横坐标在-
和0之间.
(2)令2x+1=0得x=-,y=2,
所以函数图象恒过点.
题型三 与指数函数有关的定义域和值域问题
例3 求下列函数的定义域和值域:
(1)y=;(2)y=2;(3)y=.
[解] (1)要使函数式有意义,则 1-3x≥0,即3x≤1=30,因为函数y=3x在
R上是增函数,所以x≤0.故函数y=的定义域为(-∞,0].
因为x≤0,所以0<3x≤1,所以0≤1-3x<1.
所以 ∈[0,1),即函数y= 的值域为[0,1).
(2)要使函数式有意义,则x-4≠0,解得x≠4.
所以函数y=2的定义域为{x|x≠4}.
因为≠0,所以2≠1,即函数y=2的值域为{y|y>0,且y≠1}.
(3)要使函数式有意义,则-|x|≥0,解得x=0.
所以函数y=的定义域为{x|x=0}.
因为x=0,所以=0=1,
即函数y=的值域为{y|y=1}.
金版点睛
求指数型函数的定义域和值域的一般方法
(1)求指数型函数的定义域时,先观察函数是y=ax型还是y=af(x)型.
①由于指数函数y=axa>0,且a≠1的定义域是R,所以函数y=afx的定义
域与fx的定义域相同.②对于函数y=faxa>0,且a≠1的定义域,关键是找出t=ax的值域的哪些
部分在y=ft的定义域中.
③求y=)型函数的定义域时,往往转化为解指数不等式组.
2求与指数函数有关的函数的值域时,要注意指数函数的值域为0,+∞,
还需注意:在求形如 y=afxa>0,且a≠1的函数值域时,先求得 fx的值域即
函数t=fx中t的范围,再根据y=at的单调性,列出指数不等式组,得出at的
范围,即y=afx的值域.
求下列函数的定义域和值域:
(1)y=0.3;(2)y=3;
(3)y=x2-2x-3.
解 (1)由x-1≠0得x≠1,所以函数的定义域为{x|x≠1}.
由≠0得y≠1,
所以函数的值域为{y|y>0且y≠1}.
(2)由5x-1≥0得x≥,
所以函数的定义域为.
由≥0,得y≥1,
所以函数的值域为{y|y≥1}.
(3)定义域为R.
∵x2-2x-3=(x-1)2-4≥-4,
∴x2-2x-3≤-4=16.
又∵x2-2x-3>0,
∴函数y=x2-2x-3的值域为(0,16].
1.若f(x)满足对任意的实数 a,b都有f(a+b)=f(a)·f(b)且f(1)=2,则++
+…+=( )
A.1010 B.2020 C.2019 D.1009
答案 B
解析 不妨设f(x)=2x,则==…==2,所以原式=1010×2=2020.
2.若函数y=(1-2a)x是实数集R上的增函数,则实数a的取值范围为(
)
A. B.(-∞,0)C. D.
答案 B
解析 由题意知,此函数为指数函数,且为实数集R上的增函数,所以底数
1-2a>1,解得a<0.
3.若函数y= 的定义域是(-∞,0],则a的取值范围为( )
A.a>0 B.a<1
C.0n>m>0,则指数函数①y=mx,②y=nx的图象为( )
答案 C
解析 由于00,且a≠1.
(1)求a的值;
(2)求函数y=f(x)(x≥0)的值域.
解 (1)因为函数图象经过点,
所以a2-1=,则a=.
(2)由(1)得f(x)=x-1(x≥0),
由x≥0,得x-1≥-1,
于是0