文档内容
第二学期期末练习
高一数学
注意事项:
1.答题前,考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔
填写清楚,并认真核对条形码上的准考证号、姓名,在答题卡的“条形码粘贴区”贴好条形码.
2.本次考试所有答题均在答题卡上完成.选择题必须使用2B铅笔以正确填涂方式将各小题
对应选项涂黑,如需改动,用橡皮擦除干净后再选涂其它选项.非选择题必须使用标准黑色
字迹签字笔书写,要求字体工整、字迹清楚.
3.请严格按照答题卡上题号在相应答题区内作答,超出答题区域书写的答案无效,在试卷、
草稿纸上答题无效.
4.本试卷共100分,作答时长90分钟.
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目
要求的一项.
1. i为虚数单位, ( )
A. B. C. D. 1
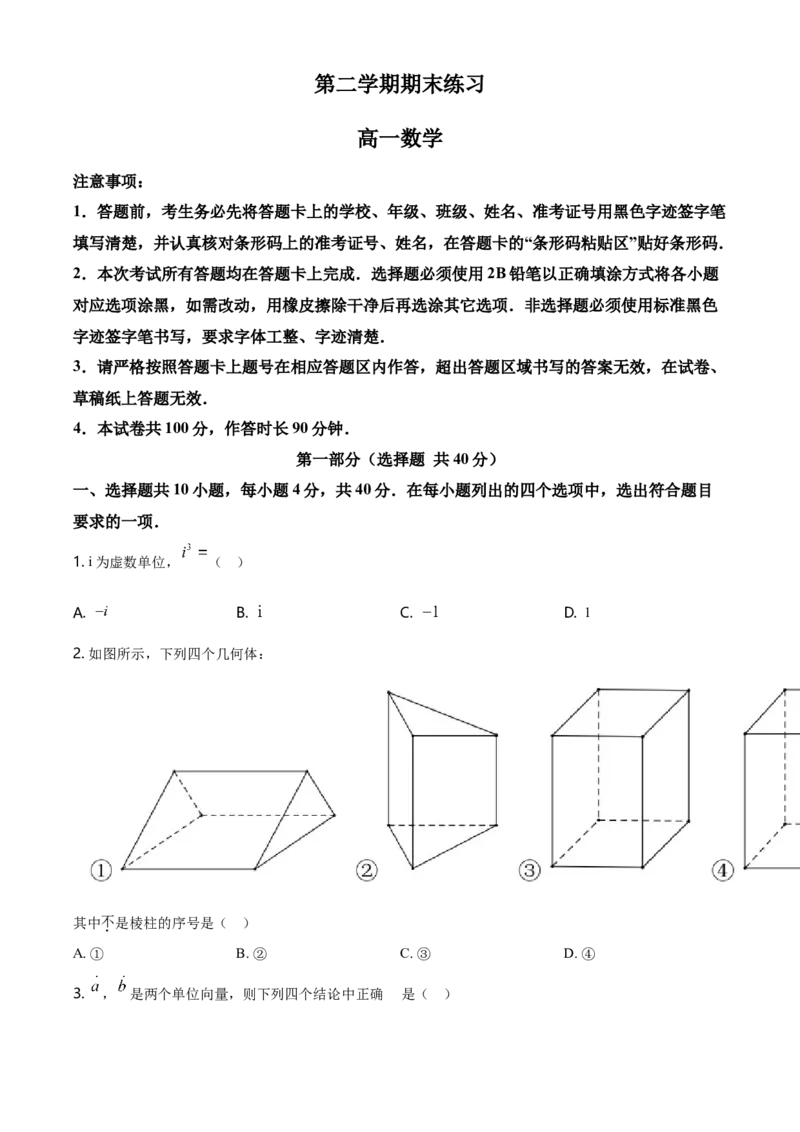
2. 如图所示,下列四个几何体:
其中不是棱柱的序号是( )
A. ① B. ② C. ③ D. ④
3. , 是两个单位向量,则下列四个结论中正确 的是( )A. B. C. D.
4. 下列命题正确的是( )
A. 三点确定一个平面 B. 一条直线和一个点确定一个平面
C. 梯形可确定一个平面 D. 圆心和圆上两点确定一个平面
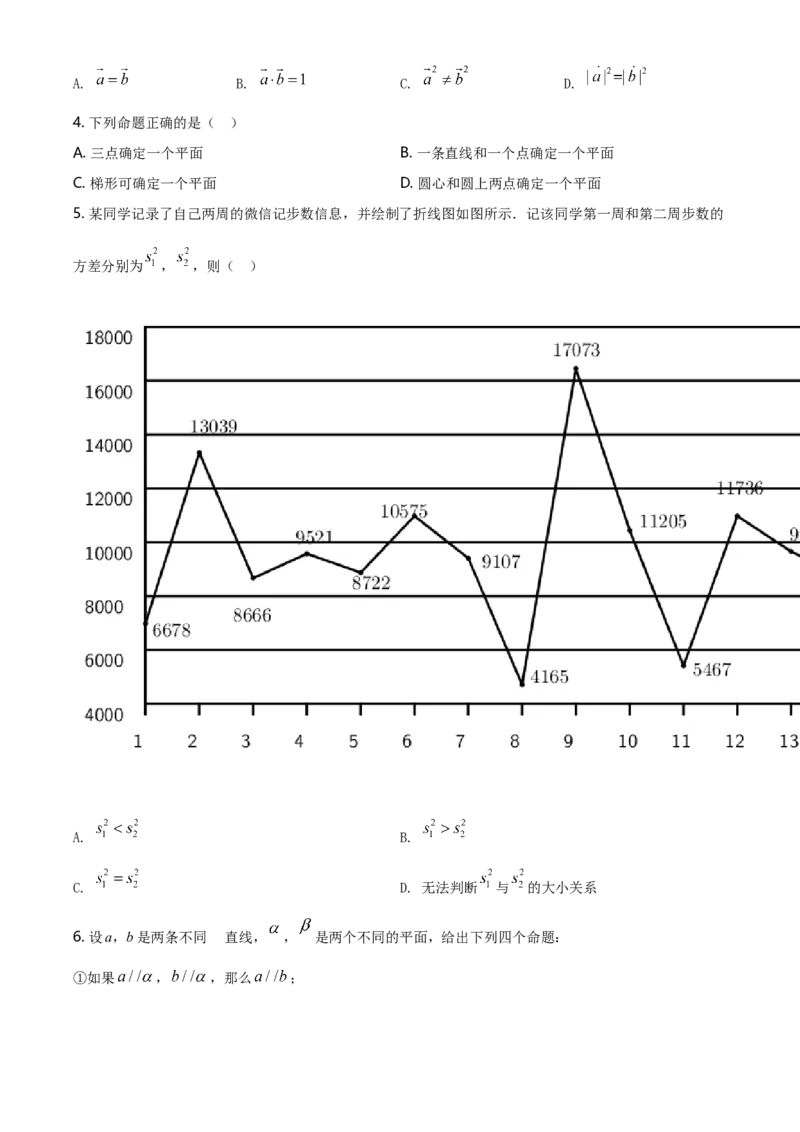
5. 某同学记录了自己两周的微信记步数信息,并绘制了折线图如图所示.记该同学第一周和第二周步数的
方差分别为 , ,则( )
A. B.
C. D. 无法判断 与 的大小关系
6. 设a,b是两条不同 的直线, , 是两个不同的平面,给出下列四个命题:
①如果 , ,那么 ;②如果 , , ,那么 ;
③如果 , ,那么 ;
④如果 , ,那么 .
其中正确命题 的序号是( )
A. ① B. ② C. ③ D. ④
7. 在 中,D是BC的中点,如果 ,那么( )
.
A , B. , C. , D. ,
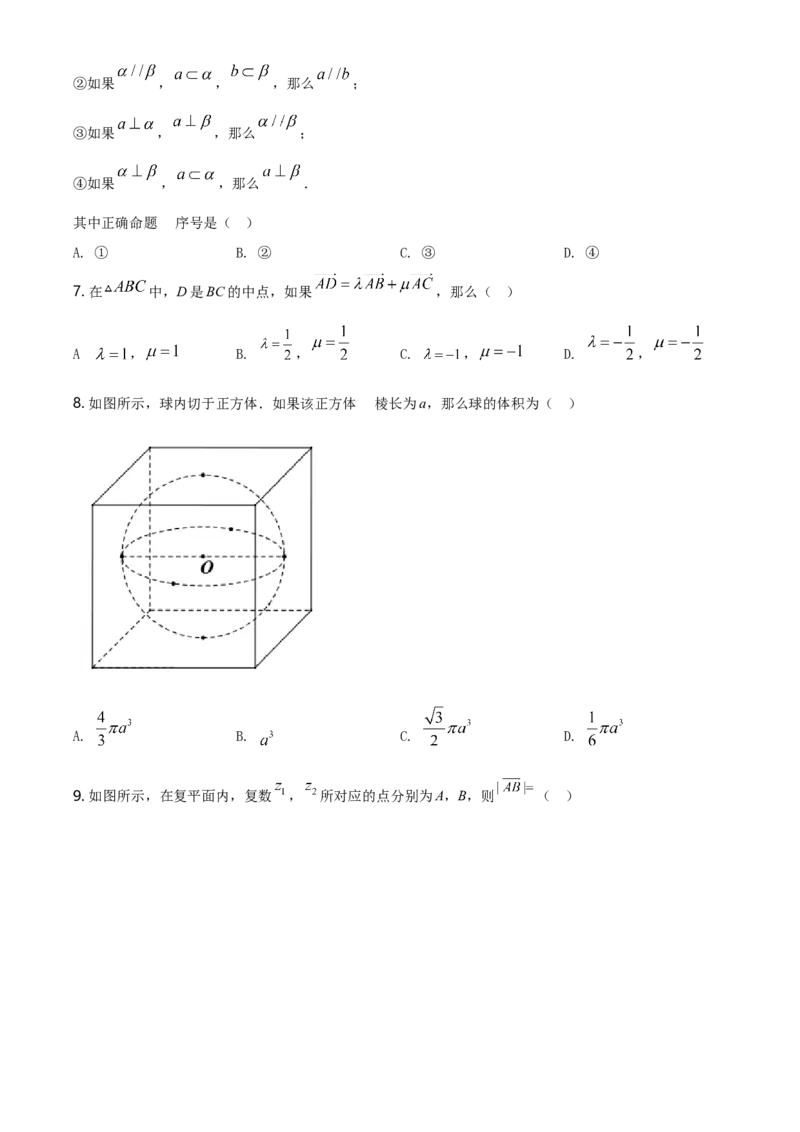
8. 如图所示,球内切于正方体.如果该正方体 的棱长为a,那么球的体积为( )
A. B. C. D.
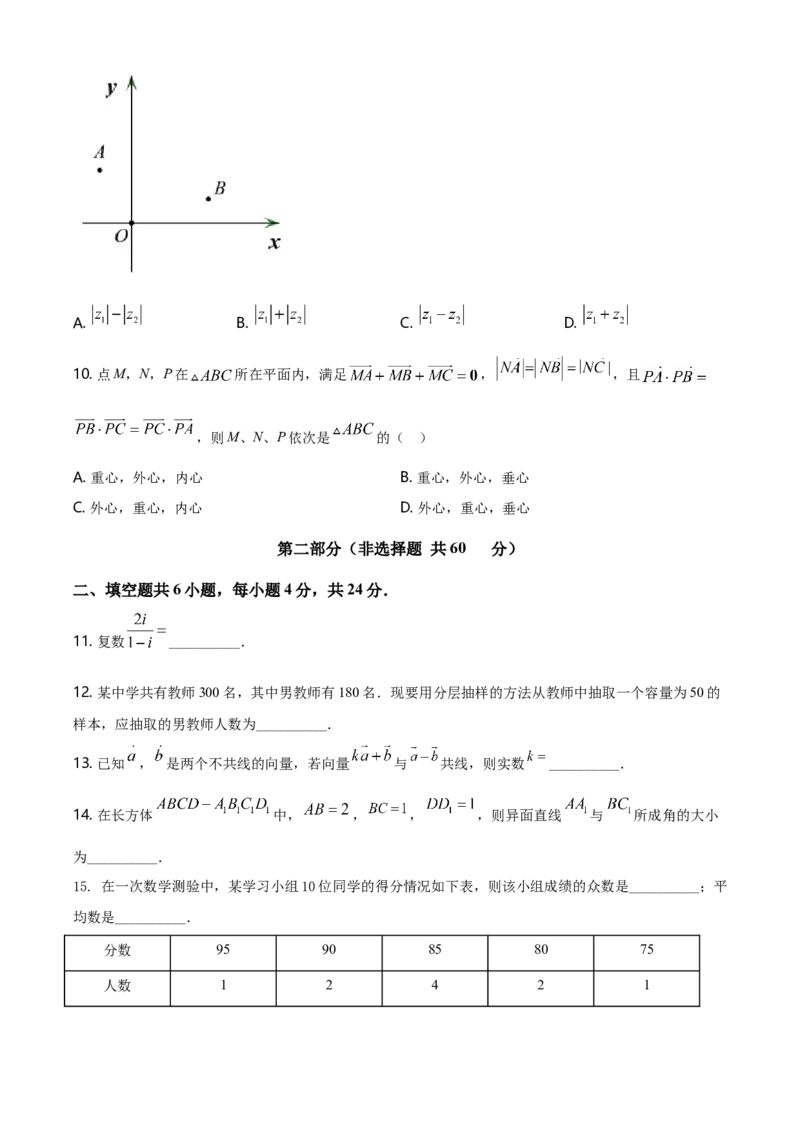
9. 如图所示,在复平面内,复数 , 所对应的点分别为A,B,则 ( )A. B. C. D.
10. 点M,N,P在 所在平面内,满足 , ,且
,则M、N、P依次是 的( )
A. 重心,外心,内心 B. 重心,外心,垂心
C. 外心,重心,内心 D. 外心,重心,垂心
第二部分(非选择题 共60 分)
二、填空题共6小题,每小题4分,共24分.
11. 复数 __________.
12. 某中学共有教师300名,其中男教师有180名.现要用分层抽样的方法从教师中抽取一个容量为50的
样本,应抽取的男教师人数为__________.
13. 已知 , 是两个不共线的向量,若向量 与 共线,则实数 __________.
14. 在长方体 中, , , ,则异面直线 与 所成角的大小
为__________.
15. 在一次数学测验中,某学习小组10位同学的得分情况如下表,则该小组成绩的众数是__________;平
均数是__________.
分数 95 90 85 80 75
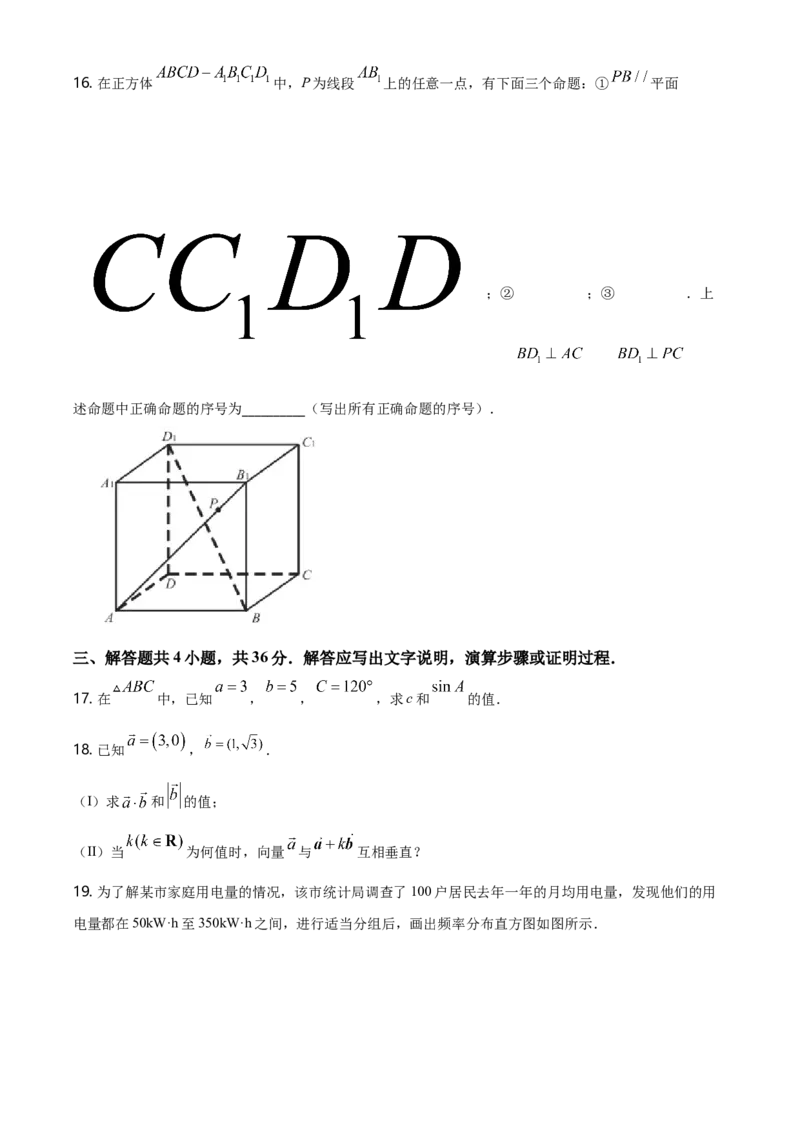
人数 1 2 4 2 116. 在正方体 中,P为线段 上的任意一点,有下面三个命题:① 平面
;② ;③ .上
述命题中正确命题的序号为__________(写出所有正确命题的序号).
三、解答题共4小题,共36分.解答应写出文字说明,演算步骤或证明过程.
17. 在 中,已知 , , ,求c和 的值.
18. 已知 , .
(Ⅰ)求 和 的值;
(Ⅱ)当 为何值时,向量 与 互相垂直?
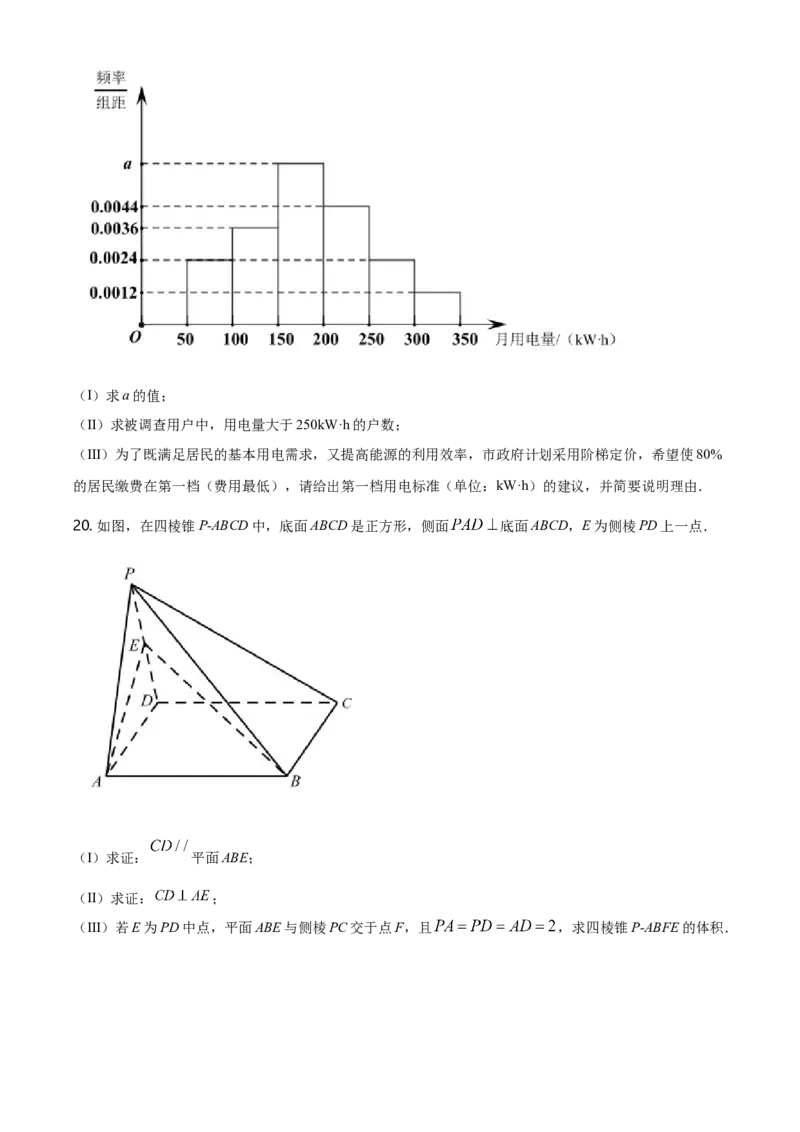
19. 为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用
电量都在50kW·h至350kW·h之间,进行适当分组后,画出频率分布直方图如图所示.(I)求a的值;
(Ⅱ)求被调查用户中,用电量大于250kW·h的户数;
(III)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使80%
的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
20. 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面 底面ABCD,E为侧棱PD上一点.
(Ⅰ)求证: 平面ABE;
(II)求证: ;
(III)若E为PD中点,平面ABE与侧棱PC交于点F,且 ,求四棱锥P-ABFE的体积.