文档内容
高一第二学期期末数学试卷
一、选择题
1. 已知点 , ,则 ( )
A. B. C. D.
2. 在复平面内复数Z=i(1﹣2i)对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 某工厂有男员工56人,女员工42人,用分层抽样的方法,从全体员工中抽出一个容量为28的样本进行
工作效率调查,其中男员工应抽的人数为( )
A. 16 B. 14 C. 28 D. 12
4. 在下列各组向量中,可以作为基底的是( )
A. ,
B. ,
.
C ,
.
D ,
5. 在空间中,下列结论正确的是( )
A. 三角形确定一个平面 B. 四边形确定一个平面
C. 一个点和一条直线确定一个平面 D. 两条直线确定一个平面
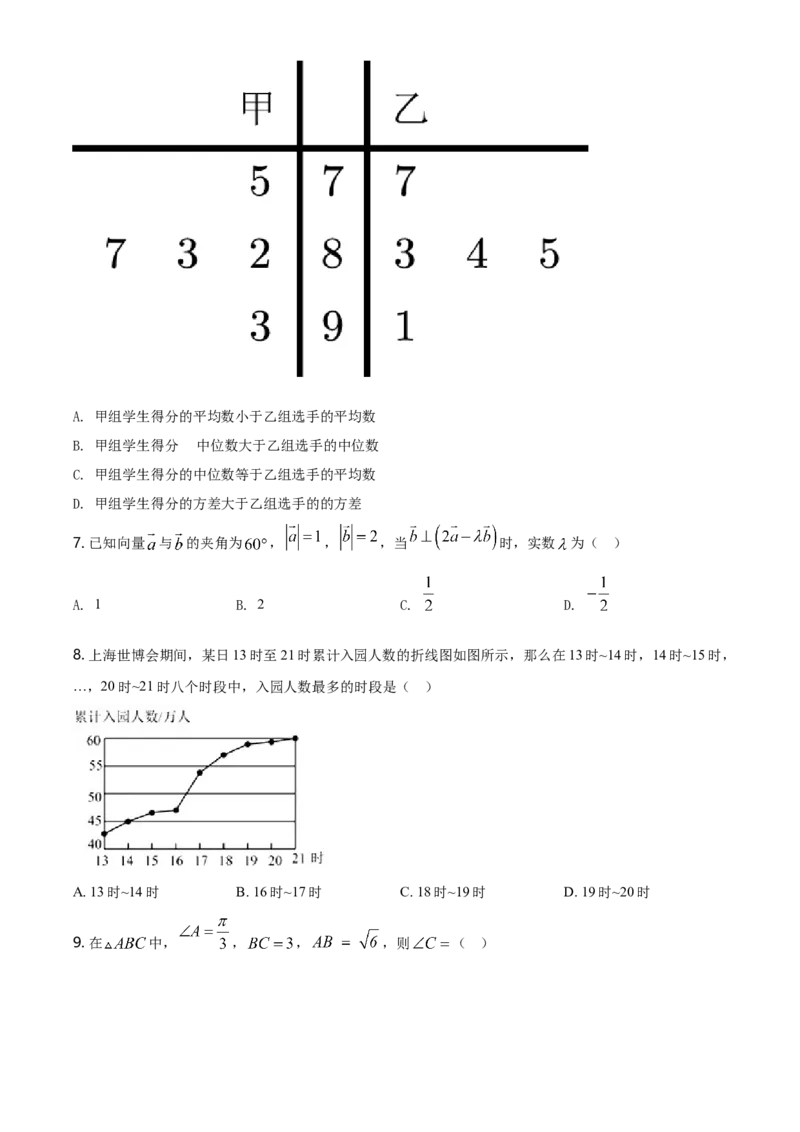
6. 新冠疫情期间,某校贯彻“停课不停学”号召,安排小组展开多向互动型合作学习,如图的茎叶图是两组
学生五次作业得分情况,则下列说法正确的是( )A. 甲组学生得分的平均数小于乙组选手的平均数
B. 甲组学生得分 的中位数大于乙组选手的中位数
C. 甲组学生得分的中位数等于乙组选手的平均数
D. 甲组学生得分的方差大于乙组选手的的方差
7. 已知向量 与 的夹角为 , , ,当 时,实数 为( )
A. 1 B. 2 C. D.
8. 上海世博会期间,某日13时至21时累计入园人数的折线图如图所示,那么在13时~14时,14时~15时,
…,20时~21时八个时段中,入园人数最多的时段是( )
A. 13时~14时 B. 16时~17时 C. 18时~19时 D. 19时~20时
9. 在 中, , , ,则 ( )A. B. 或 C. D. 或
10. 点 , 分别是棱长为2的正方体 中棱 , 的中点,动点 在正方形
(包括边界)内运动.若 面 ,则 的长度范围是( )
A. B. C. D.
二、填空题
11. 已知复数 ,则复数 ______.
12. 已知l,m是平面 外的两条不同直线.给出下列三个论断:
①l⊥m;②m∥ ;③l⊥ .
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.
13. 如图,在 中, .若 ,则 的值为______,P是 上的一点,若
,则m的值为______.14. 将底面直径为8,高为 的圆锥体石块打磨成一个圆柱,则该圆柱侧面积的最大值为______.
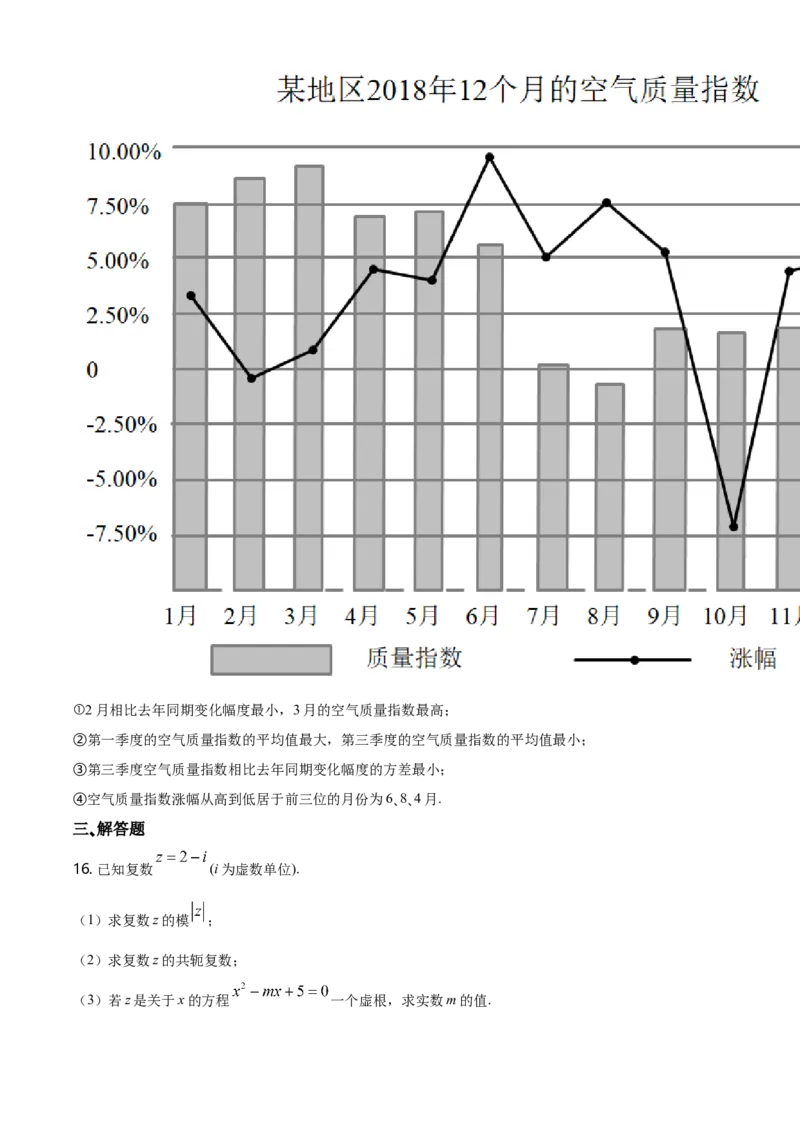
15. 如图是某地区2018年12个月的空气质量指数以及相比去年同期变化幅度的数据统计图表,根据图表,
下面叙述正确的是______.①2月相比去年同期变化幅度最小,3月的空气质量指数最高;
②第一季度的空气质量指数的平均值最大,第三季度的空气质量指数的平均值最小;
③第三季度空气质量指数相比去年同期变化幅度的方差最小;
④空气质量指数涨幅从高到低居于前三位的月份为6、8、4月.
三、解答题
16. 已知复数 (i为虚数单位).
(1)求复数z的模 ;
(2)求复数z的共轭复数;
(3)若z是关于x的方程 一个虚根,求实数m的值.17. 已知向量 与 , , .
(1)求 ;
(2)设 , 的夹角为 ,求 的值;
(3)若向量 与 互相平行,求k的值.
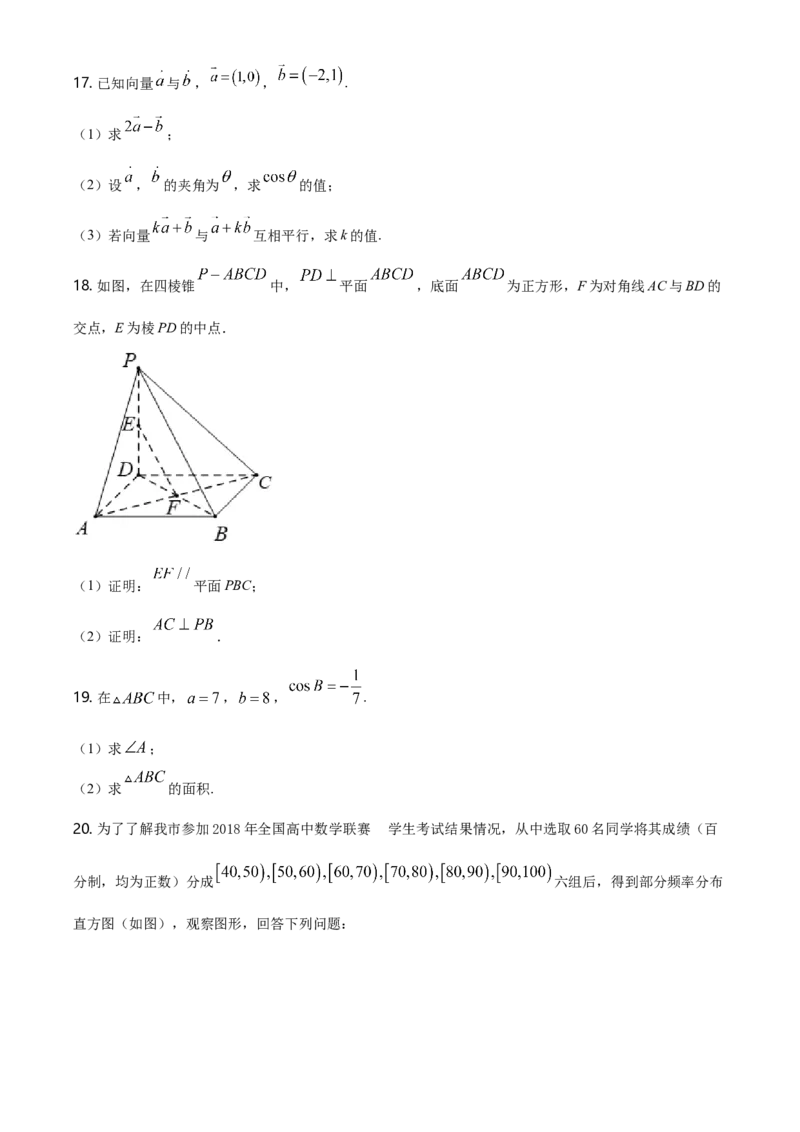
18. 如图,在四棱锥 中, 平面 ,底面 为正方形,F为对角线AC与BD的
交点,E为棱PD的中点.
(1)证明: 平面PBC;
(2)证明: .
19. 在 中, , , .
(1)求 ;
(2)求 的面积.
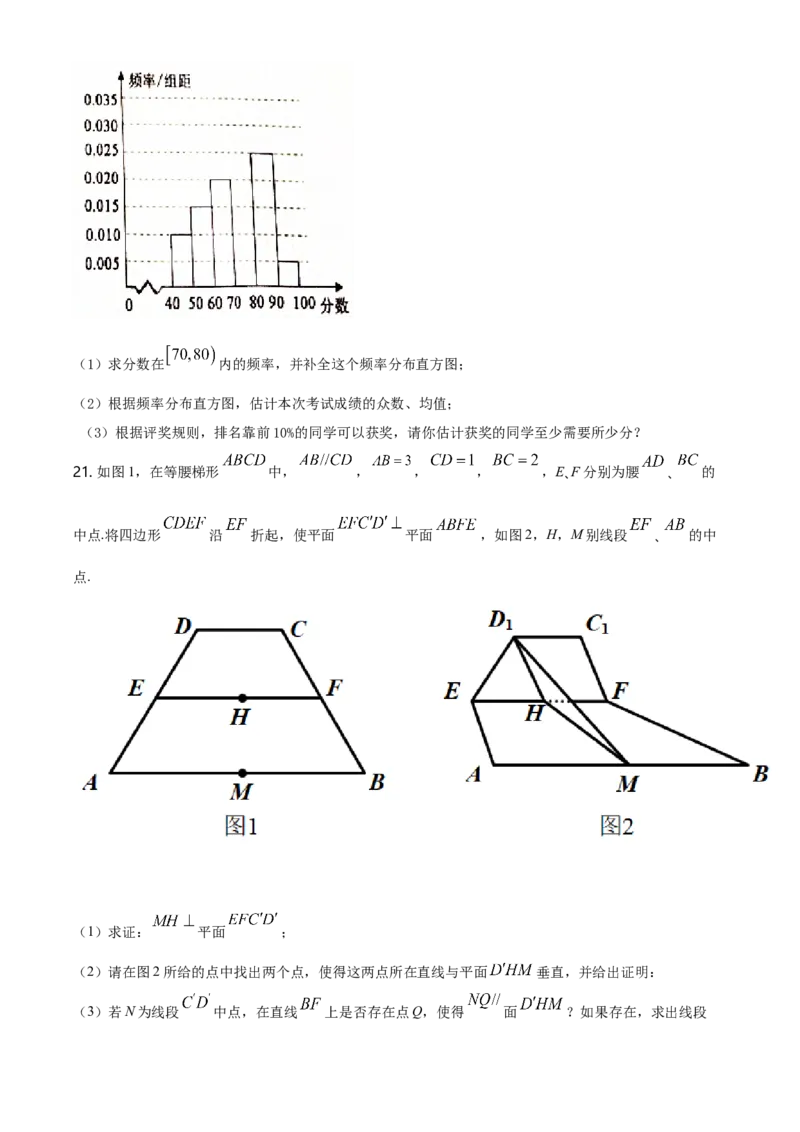
20. 为了了解我市参加2018年全国高中数学联赛 的学生考试结果情况,从中选取60名同学将其成绩(百
分制,均为正数)分成 六组后,得到部分频率分布
直方图(如图),观察图形,回答下列问题:(1)求分数在 内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试成绩的众数、均值;
(3)根据评奖规则,排名靠前10%的同学可以获奖,请你估计获奖的同学至少需要所少分?
21. 如图1,在等腰梯形 中, , , , ,E、F分别为腰 、 的
中点.将四边形 沿 折起,使平面 平面 ,如图2,H,M别线段 、 的中
点.
(1)求证: 平面 ;
(2)请在图2所给的点中找出两个点,使得这两点所在直线与平面 垂直,并给出证明:
(3)若N为线段 中点,在直线 上是否存在点Q,使得 面 ?如果存在,求出线段的长度,如果不存在,请说明理由.