数学-广东省2023-2024学年高三下学期开学考试大联考(1)_2024年2月_022月合集_2024届广东省2月高三下学期开学考试金太阳联考（278C）

高三数学 注意事项： 1.答题前，考生务必将自已的姓名，为生号，考场号，座位号填写在答题卡上. 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题号的答案标号涂黑.如需改动， 用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上 无效. 3.考试结束后，将本试卷和答题卡一并交回. 4.本试卷主要考试内容：高考全部内容. 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是符 合题目要求的. 1.已知集合A=-1,0,1,2,B={x| x-1 >1}，则AÇB=（ ） A. 0 B. -1 C. -1,0,1 D. -1,0,1,2 2. 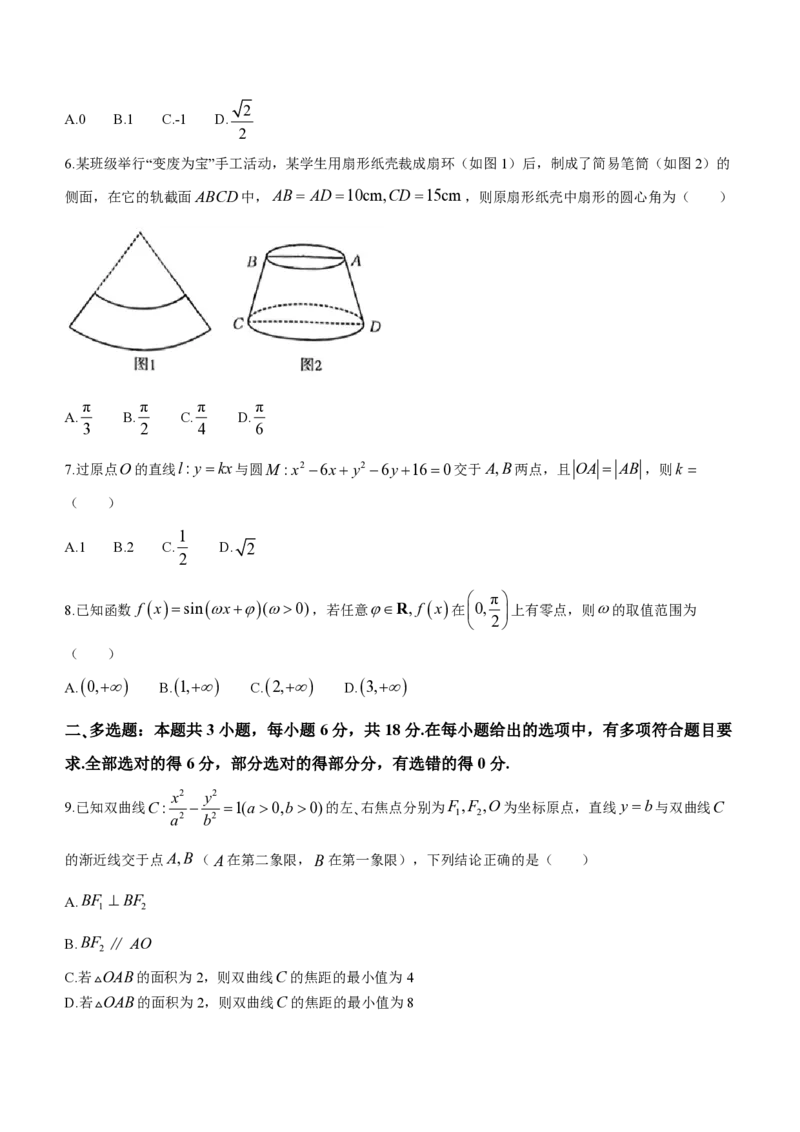3+2i2-2i=（ ） A.-10+2i B.-10-2i C.10+2i D.10-2i 3.已知 f  2x = x，则 f 3=（ ） A.8 B.9 C.log 3 D.log 2 2 3 4.国家统计局发布的2018年至2022年我国居民消费水平情况如图所示，则下列说法正确的是（ ） 农村居民消费水平 ´ 农村人口数+城镇居民消费水平 ´ 城镇人口数 （居民消费水平： ） 农村人口数+城镇人口数 A.2018年至2022年我国居民消费水平逐年提高 B.2018年至2022年我国城镇居民消费水平逐年提高 C.2018年至2022年我国居民消费水平数据的60%分位数为27504元 D.2022年我国城镇人口数比农村人口数的1.5倍还要多 æ πö æ πö æ πö 5.已知sin ç a- ÷ +cos ç a- ÷ =sina，则tan ç a- ÷ =（ ） è 4ø è 4ø è 4ø 学科网（北京）股份有限公司2 A.0 B.1 C.-1 D. 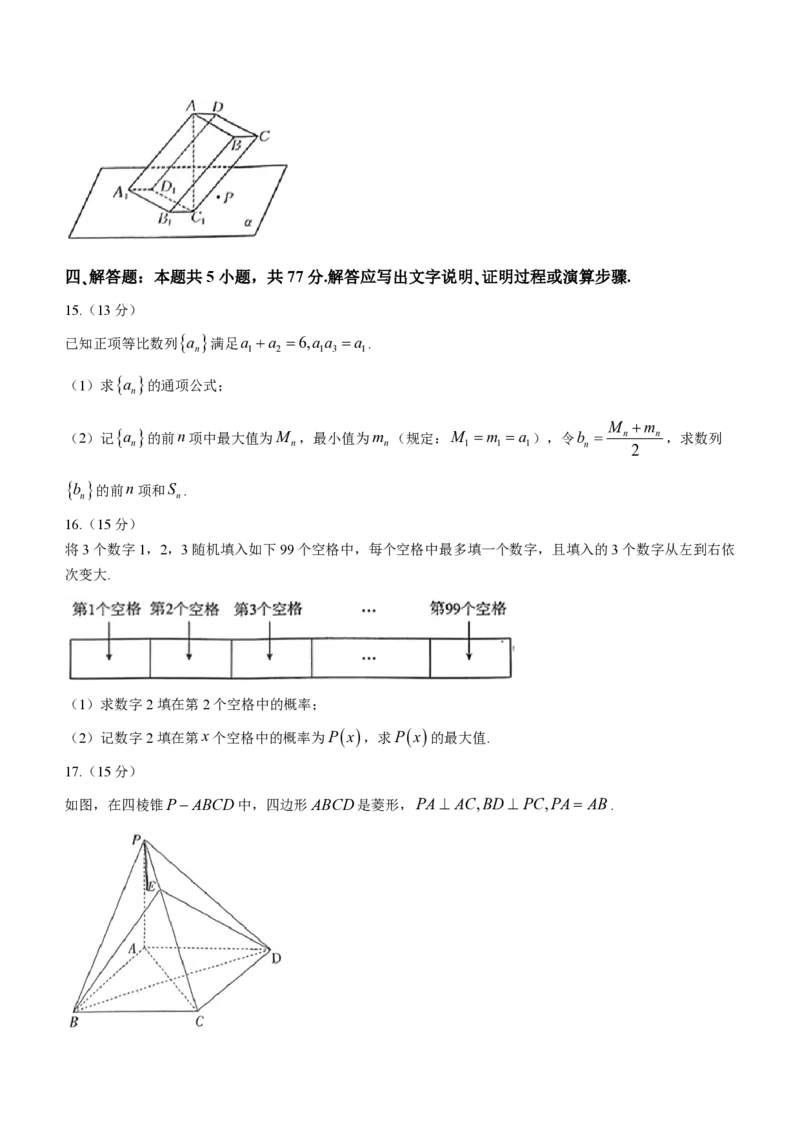2 6.某班级举行“变废为宝”手工活动，某学生用扇形纸壳裁成扇环（如图1）后，制成了简易笔筒（如图2）的 侧面，在它的轨截面ABCD中，AB= AD=10cm,CD=15cm，则原扇形纸壳中扇形的圆心角为（ ） π π π π A. B. C. D. 3 2 4 6 7.过原点O的直线l: y =kx与圆M :x2 -6x+ y2 -6y+16=0交于A,B两点，且 OA = AB ，则k = （ ） 1 A.1 B.2 C. D. 2 2 æ πö 8.已知函数 f x=sinwx+j(w>0)，若任意jÎR, f x 在ç 0, ÷上有零点，则w的取值范围为 è 2ø （ ） A. 0,+¥ B. 1,+¥ C. 2,+¥ D. 3,+¥ 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目要 求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. x2 y2 9.已知双曲线C: - =1(a >0,b>0)的左､右焦点分别为F,F ,O为坐标原点，直线y =b与双曲线C a2 b2 1 2 的渐近线交于点A,B（A在第二象限，B在第一象限），下列结论正确的是（ ） A.BF ^ BF 1 2 B.BF ∥ AO 2 C.若 OAB的面积为2，则双曲线C的焦距的最小值为4 V D.若 OAB的面积为2，则双曲线C的焦距的最小值为8 V 学科网（北京）股份有限公司10.如图，三角形数阵由一个等差数列2,5,8,11,14, L排列而成，按照此规律，下列结论正确的是（ ） A.数阵中前7行所有数的和为1190 B.数阵中第8行从左至右的第4个数是101 C.数阵中第10行的第1个数是137 D.数阵中第10行从左至右的第4个数是146 11.已知定义在R上的函数 f x 满足 f xé ë f x- f x- yù û = f xy ，当xÎ-¥,0È0,+¥ ，时， f x¹0.下列结论正确的是（ ） æ1ö 1 A. f ç ÷ = B. f 10=1 è2ø 2 C. f x 是奇函数 D. f x 在R上单调递增 三､填空题：本题共 3小题，每小题 5分，共 15分. æ p ö 12.已知抛物线C: y2 =2px(p >0)的焦点为F ，点P ç ,a ÷在抛物线C上，且 PF =3，则 p= è 4 ø __________. 13.甲､乙两位同学进行羽毛球比赛，约定赛制如下：累计赢2局者胜，分出胜负即停止比赛.已知甲每局赢的 3 概率为 ，每局比赛的结果相互独立.本次比赛到第3局才分出胜负的概率为__________，本次比赛甲获胜的 5 概率为__________. 14.如图，将正四棱柱ABCD-ABC D 斜立在平面a上，顶点C 在平面a内，AC ^平面 1 1 1 1 1 1 a,AA =2AB=6.点P在平面a内，且PC = 3.若将该正四棱柱绕AC 旋转，PC的最大值为 1 1 1 __________. 学科网（北京）股份有限公司四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 15.（13分） 已知正项等比数列 a  满足a +a =6,aa =a . n 1 2 1 3 1 （1）求 a  的通项公式； n M +m （2）记 a  的前n项中最大值为M ，最小值为m （规定：M =m =a ），令b = n n ，求数列 n n n 1 1 1 n 2 b  的前n项和S . n n 16.（15分） 将3个数字1，2，3随机填入如下99个空格中，每个空格中最多填一个数字，且填入的3个数字从左到右依 次变大. （1）求数字2填在第2个空格中的概率； （2）记数字2填在第x个空格中的概率为Px ，求Px 的最大值. 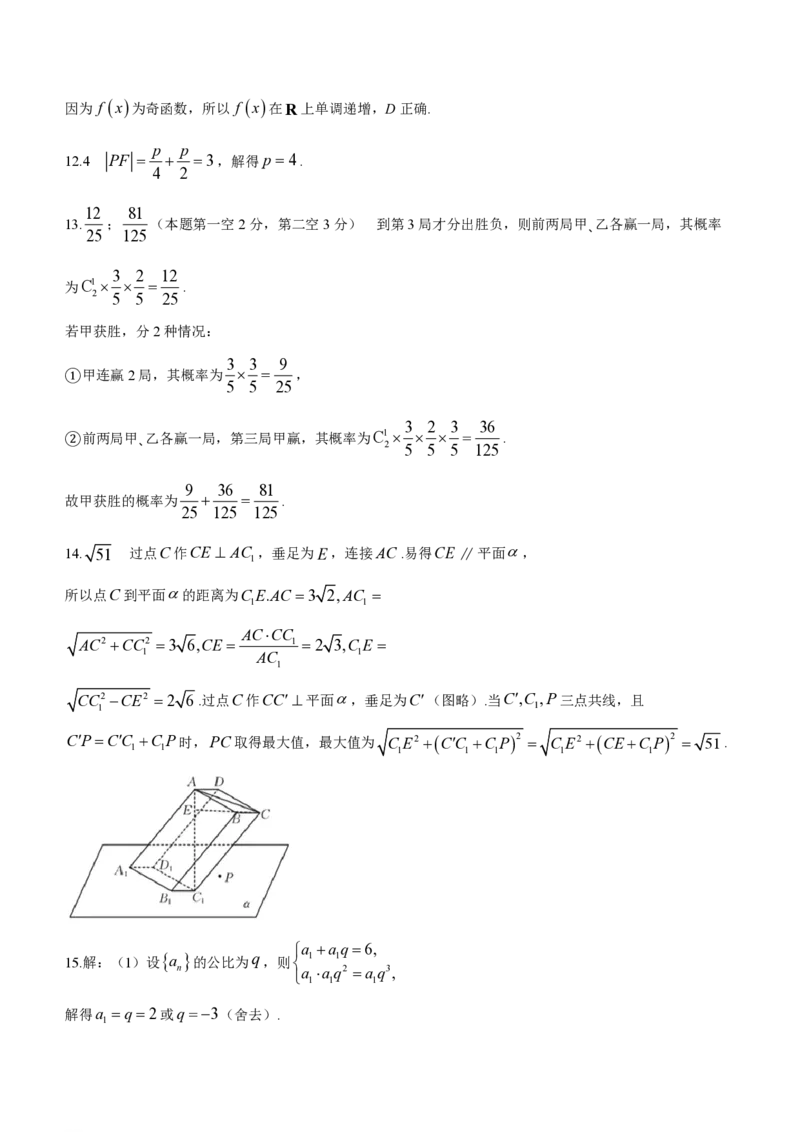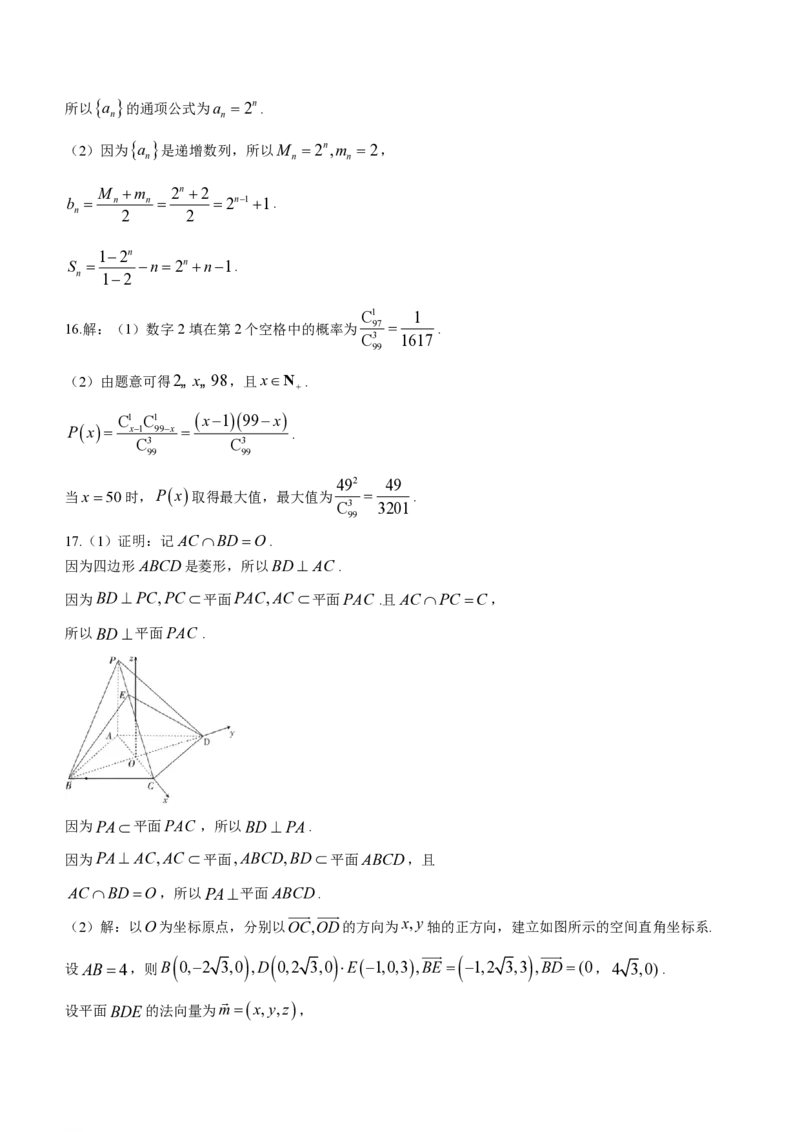17.（15分） 如图，在四棱锥P-ABCD中，四边形ABCD是菱形，PA^ AC,BD^ PC,PA= AB. 学科网（北京）股份有限公司（1）证明：PA^平面ABCD. uuur uuur （2）若PC =4PE,ÐABC =60o，求二面角A-BD-E的余弦值. 18.（17分） x2 y2 1 已知椭圆C的方程为 + =1(a >b>0)，右焦点为F1,0 ，且离心率为 a2 b2 2 （1）求椭圆C的方程； 2 æ 3ö 25 （2）过点F 的直线l与椭圆C交于A,B两点，证明，圆 ç x- ÷ + y2 = 恒与以弦AB为直径的圆相切. è 4ø 16 19.（17分） 已知函数 f x= 2x-a. （1）若曲线y = f x 在点  a, f a 处的切线过点 4,2 ，求a的值； （2）若 f x„ aex-1恒成立，求a的取值范围. 学科网（北京）股份有限公司高三数学参考答案 1.B B=-¥,0È2,+¥,AÇB=-1 . 2.D 3+2i2-2i=6-6i+4i-4i2 =10-2i. 3.C 令2x =3，可得x=log 3，则 f 3=log 3. 2 2 4.D 2019年的居民消费水平比2020年的居民消费水平高，A错误.2019年的城镇居民消费水平比2020年的 城镇居民消费水平高，B错误.2018年至2022年我国居民消费水平数据从小到大排序为 25245,27439,27504,31013,31718,5´60%=3,2018年至2022年我国居民消费水平数据的60%分位数为 27504+31013 =29258.5元，C错误.设我国农村人口数为x，城镇人口数为 y ，则 2 19530x+38289y y 12188 3 31718= ，化简得 = > ，所以2022年我国城镇人口数比农村人口数的1.5倍 x+ y x 6571 2 还要多，D正确. æ πö æ πö 5.C 因为sin ç a- ÷ +cos ç a- ÷ = 2sina，所以 2sina=sina，则sina=0，即a=kπ,kÎZ， è 4ø è 4ø æ πö æ πö 所以tan ç a- ÷ =tan ç kπ- ÷ =-1. è 4ø è 4ø 6.B 延长CB,DA交于点O，设圆台上､下个底面的闪心分别为O ,O .连接OO ， 2 1 1 r OB 设OB= x,O 2 B=r,O 1 C = R.因为 V OO 2 B∽ V OO 1 C，所以 R = OC ， 2πr π 则x=20cm.设所求圆心角为q，则xq=2πr，所以q= = . x 2 学科网（北京）股份有限公司7.A 圆M :x2 -6x+ y2 -6y+16=0，即圆M :(x-3)2 +(y-3)2 =2，圆心M 3,3 到直线l的距离为 d,AB的中点为C.因为 OA = AB ，所以 OC =3 AC .因为 OM = 32 +32 =3 2，所以 OC = |OM |2 -d2 = 18-d2 .又因为 AC = 2-d2 ，所以 18-d2 =3 2-d2 ，解得d =0，所以 3-0 直线l经过圆心M 3,3 ，所以k = =1. 3-0 æ πw ö 8.C 令t =wx+j，由题意可得sint =0在ç j, +j ÷上有解. è 2 ø πw 因为sint =0在 a,b 内有解的最短区间长度为b-a=π.所以 +j-j>π，解得w>2. 2 9.AC OB =c= OF = OF ，点B在以O为圆心， OF 为半径的圆上，所以BF ^ BF ，A正确.直线 1 2 1 1 2 b b b b BF 的斜率为- ，直线AO的斜率为- ,- 与- 不一定相等，所以直线BF 与直线AO不一定 2 c-a a c-a a 2 1 平行，B错误. V OAB的面积为 ×2a×b=ab=2，双曲线C的焦距为2c=2 a2 +b2…2 2ab =2 4 =4， 2 当且仅当a=b= 2时，等号成立，所以双曲线C的焦距的最小值为4,C正确，D错误. 10.ACD 设等差数列2,5,8,11,14, L的通项公式为b n =3n-1.数阵中前7行共1+2+3+ L +7=28个数， 28´27´3 数阵中前7行所有数的和为2´28+ =1190，A正确. 2 令b =3n-1=101，解得n=34，前7行共28个数，第8行有8个数，所以101是数阵中第8行从左至右 n 的第6个数，B错误.记每一行的第1个数组成数列 a  ，则 n a 1 =2,a 2 -a 1 =3,a 3 -a 2 =6=3´2,a 4 -a 3 =9=3´3, L ,a n -a n-1 =3´n-1 ，累加得 学科网（北京）股份有限公司3nn-1 3n2 -3n+4 a -a =3´1+2+3+ +n-1= ，所以a = ,a =137，C正确.数阵中第10行 n 1 L 2 n 2 10 从左至右的第4个数是137+4-1´3=146，D正确. 11.ACD 令x= y =0，可得 f 0=0. 令x= y =1，可得[f 1]2 = f 1 .因为当x >0时， f x¹0，所以 f 1=1. 令 x= y ，可得[f x]2 = f  x2 …0. 因为x2…0，所以当x…0时， f x…0. 又因为当x >0时， f x¹0，所以当x >0时， f x>0. 令y=1，可得 f xé ë f x- f x-1ù û = f x ，① 所以 f x- f x-1=1, f x+1- f x=1，两式相加可得 f x+1- f x-1=2. 令y =-1，可得 f xé ë f x- f x+1ù û = f -x .② ①-②可得 f xé ë f x+1- f x-1ù û = f x- f -x ，化简可得 f x=-f -x ，所以 f x 是奇函 数，C正确. 由 f x- f x-1=1，可得 f 2= f 1+1=2, f 3= f 2+1=3, f 4= f 3+1=4, L , f 10=10，B错误. ì æ1ö æ 1ö f - f - =1, ìïf x+1- f x=1, ï ï ç è2 ÷ ø ç è 2 ÷ ø æ1ö 1 由í 可得í 解得 f ç ÷ = ,A正确. ïî f x=-f -x, ï æ1ö æ 1ö è2ø 2 f =-f - , ç ÷ ç ÷ ï î è2ø è 2ø f  x x -x  令x= x ,y = x -x ，可得 f x - f x = 1 1 2 . 1 1 2 1 2 f x  1 令0< x < x ，则x -x >0,x x -x >0. 2 1 1 2 1 1 2 因为当x >0时， f x>0，所以 f x >0, f  x x -x  >0， 1 1 1 2 f  x x -x  所以 f x - f x = 1 1 2 >0，即 f x > f x  ， 1 2 f x  1 2 1 所以 f x 在 0,+¥ 上单调递增. 学科网（北京）股份有限公司因为 f x 为奇函数，所以 f x 在R上单调递增，D正确. p p 12.4 PF = + =3，解得 p=4. 4 2 12 81 13. ； （本题第一空2分，第二空3分） 到第3局才分出胜负，则前两局甲､乙各赢一局，其概率 25 125 3 2 12 为C1 ´ ´ = . 2 5 5 25 若甲获胜，分2种情况： 3 3 9 ①甲连赢2局，其概率为 ´ = ， 5 5 25 3 2 3 36 ②前两局甲､乙各赢一局，第三局甲赢，其概率为C1 ´ ´ ´ = . 2 5 5 5 125 9 36 81 故甲获胜的概率为 + = . 25 125 125 14. 51 过点C作CE ^ AC ，垂足为E，连接AC.易得CE∥平面a， 1 所以点C到平面a的距离为C E.AC =3 2,AC = 1 1 AC×CC AC2 +CC2 =3 6,CE = 1 =2 3,C E = 1 AC 1 1 CC2 -CE2 =2 6.过点C作CC¢^平面a，垂足为C¢（图略）.当C¢,C ,P三点共线，且 1 1 C¢P=C¢C +C P时，PC取得最大值，最大值为 C E2 +C¢C +C P2 = C E2 +CE+C P2 = 51. 1 1 1 1 1 1 1 ìa +aq =6, 15.解：（1）设 a  的公比为 q ，则í 1 1 n a ×aq2 =aq3, î 1 1 1 解得a =q=2或q =-3（舍去）. 1 学科网（北京）股份有限公司所以 a  的通项公式为a =2n. n n （2）因为 a  是递增数列，所以M =2n,m =2， n n n M +m 2n +2 b = n n = =2n-1+1. n 2 2 1-2n S = -n=2n +n-1. n 1-2 C1 1 16.解：（1）数字2填在第2个空格中的概率为 97 = . C3 1617 99 （2）由题意可得2„ x„ 98，且xÎN . + C1 C1 x-199-x Px= x-1 99-x = . C3 C3 99 99 492 49 当x=50时，Px 取得最大值，最大值为 = . C3 3201 99 17.（1）证明：记ACÇBD=O. 因为四边形ABCD是菱形，所以BD^ AC. 因为BD^ PC,PC Ì平面PAC,AC Ì平面PAC .且ACÇPC =C， 所以BD^平面PAC . 因为PAÌ平面PAC ，所以BD^ PA. 因为PA^ AC,AC Ì平面,ABCD,BDÌ平面ABCD，且 ACÇBD=O，所以PA^平面ABCD. uuur uuur x,y （2）解：以O为坐标原点，分别以OC,OD的方向为 轴的正方向，建立如图所示的空间直角坐标系.     uuur   uuur 设AB=4，则B 0,-2 3,0 ,D 0,2 3,0 ×E-1,0,3,BE = -1,2 3,3 ,BD=(0，4 3,0). 设平面BDE的法向量为m r =x,y,z ， 学科网（北京）股份有限公司uuur ì ïm r ×BD=4 3y =0. 则í 令x=3，得m r =3,0,1 . uuur r ïîm×BE =-x+2 3y+3z =0, 平面ABD的一个法向量为n r =0,0,1 . r r n×m 1 10 r r cos n,m = = = ， r r n m 10 10 10 易得二面角A-BD-E为锐角，故二面角A-BD-E的余弦值为 . 10 c 1 18.（1）解：由题意得椭圆C的半焦距c=1，且e= = ，所以a = 2. a 2 x2 y2 又因为b2 =a2 -c2 =3，所以椭圆C的方程为 + ==1. 4 3 （2）证明：当直线l的斜率为0时，直线l的方程为x =0 此时AB为椭圆C的长轴，以弦AB为直径的圆的方程为x2 + y2 =4，该圆的半径为2. æ 3ö 2 25 5 5 3 圆 ç x- ÷ + y2 = 的半径为 ，两圆的圆心距为2- = . è 4ø 16 4 4 4 2 æ 3ö 25 满足圆 ç x- ÷ + y2 = 恒与以弦AB为直径的圆相切. è 4ø 16 当直线l的斜率不为0时，设直线l的方程为x=ty+1,Ax ,y ,Bx ,y ,AB的中点为M x ,y  . 1 1 2 2 0 0 ìx=ty+1, 联立 ï íx2 y2 得  3t2 +4  y2 +6ty-9=0， + =1, ï î 4 3 6t 9 所以y + y =- ,y y =- ， 1 2 3t2 +4 1 2 3t2 +4 y + y 3t 4 y = 1 2 =- ,x =ty +1= . 0 2 3t2 +4 0 0 3t2 +4 12  t2 +1  AB = 1+t2 y + y 2 -4y y = . 1 2 1 2 3t2 +4 æ 3ö 2 25 æ3 ö 记圆 ç x- ÷ + y2 = 的圆心为N ç ,0 ÷， è 4ø 16 è4 ø 学科网（北京）股份有限公司æ 4 3ö 2 æ 3t ö 2 9t2 +4 MN = ç - ÷ + ç - ÷ = . è3t2 +4 4ø è 3t2 +4ø 4  3t2 +4  1 6  t2 +1  9t2 +4 5  3t2 +4  5 AB - MN = - = = . 2 3t2 +4 4  3t2 +4  4  3t2 +4  4 2 æ 3ö 25 满足圆 ç x- ÷ + y2 = 恒与以弦AB为直径的圆相切. è 4ø 16 2 æ 3ö 25 综上，圆 ç x- ÷ + y2 = 恒与以弦AB为直径的圆相切. è 4ø 16 1 1 19.解：（1） f a= a, f¢x= , f¢a= . 2x-a a 1 曲线y = f x 在点  a, f a 处的切线方程为y- a = x-a . a 1 因为该场线过点 4,2 ，所以2- a = 4-a ，解得a = 4. a a （2）因为 f x= 2x-a„ aex-1，所以a >0，且x> . 2 两边平方可得a2e2x-2…2x-a. 令函数gx=a2e2x-2 -2x+a æ ç x> aö ÷ ,g¢x=2  a2e2x-2 -1  . è 2ø 令函数hx=a2e2x-2 -1,h¢x=2a2e2x-2 >0，所以hx 是增函数. 令g¢x=2  a2e2x-2 -1  =0，得x=1-lna. a 下面比较1-lna与 的大小. 2 a a+2 令函数ua=1-lna- ,u¢a=- <0,ua是减函数. 2 2a 1 因为u1= >0,u2=-ln2<0，所以存在a Î1,2 ，使得当aÎ0,a  时，ua>0， 2 0 0 a a 即1-lna > .当aÎa ,+¥ 时，ua„ 0，即1-lna„ . 2 0 2 学科网（北京）股份有限公司当aÎ0,a  时， 0 æa ö 当xÎ ç ,1-lna ÷时，hx<0，即g¢x<0； è2 ø 当xÎ1-lna,+¥ 时，hx>0，即g¢x>0. æa ö 所以gx 在ç ,1-lna ÷上单调递减，在 1-lna,+¥ 上单调递增. è2 ø g(x) = g1-lna=a2e-2lna -21-lna+a=2lna+a-1. min 2 令函数va=2lna+a-1,v¢a= +1>0，所以va 是增函数. a 由题意可得g(x) =2lna+a-1…0，又因为v1=0，所以1„ a0，符合题意. 0 min è2ø 综上，a的取值范围为 1,+¥ . 学科网（北京）股份有限公司