文档内容
高一数学期中考试
命题人:夏俊东 审题人:王进
一、单选题(选对得5分,选错得0分)
1. 设复数 满足 ,则 ( )
A. B. 4 C. D.
【答案】A
【解析】
【分析】由复数的四则运算结合几何意义得出 .
【详解】
故选:A
2. 已知 、 是平面内所有向量的一组基底,则下列四组向量中,不能作为基底的一组是( )
A. 和 B. 和
C. 和 D. 和
【答案】B
【解析】
【分析】判断各选项向量组是否共线即可得出答案.
【详解】因为 ,所以 和 共线,所以 和 不能
作为基底.
故选:B.
3. 已知直线 和平面 ,下列说法正确的是( )
A. 若 // , // ,则 // B. 若 // , ,则 //
C. 若 // , , ,则 // D. 若 // , // ,则 //
【答案】C
第1页/共22页
学科网(北京)股份有限公司【解析】
【分析】根据线面平行的判定和性质,对每个选项进行逐一分析,即可判断和选择.
【详解】对 :若 // , // ,则 // 或 ,故 错误;
对 :若 // , ,则 // 或 ,故 错误;
对 :若 // , , ,则 // ,故 正确;
对 :若 // , // ,则 可以平行,可以相交,也可以是异面直线,故 错误;
故选: .
4. 已知某圆锥的母线长为2,其轴截面为直角三角形,则圆锥的体积为( )
A. B. C. D.
【答案】A
【解析】
【分析】由圆锥的结构特征求出底面半径、高,再应用圆锥的体积公式求体积.
【详解】由题意,圆锥的底面半径 ,圆锥的高 ,
所以圆锥的体积 .
.
故选:A
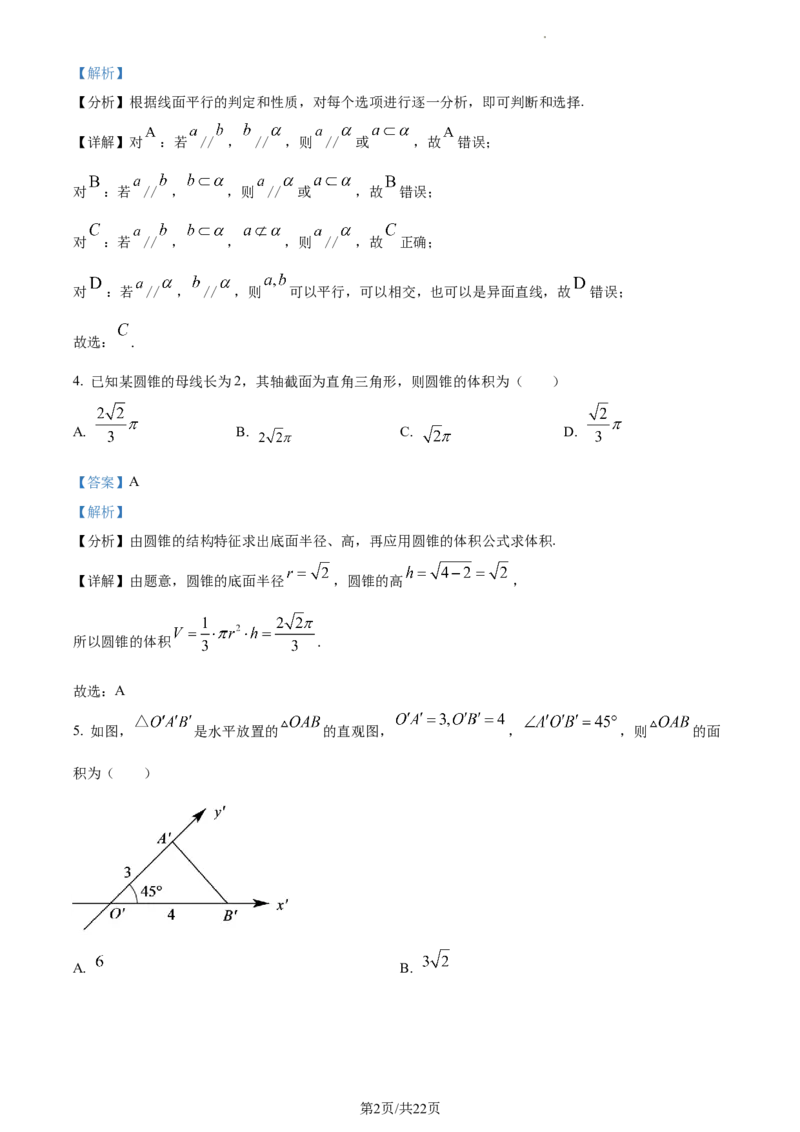
5. 如图, 是水平放置的 的直观图, , ,则 的面
积为( )
A. B.
第2页/共22页
学科网(北京)股份有限公司C. D.
【答案】C
【解析】
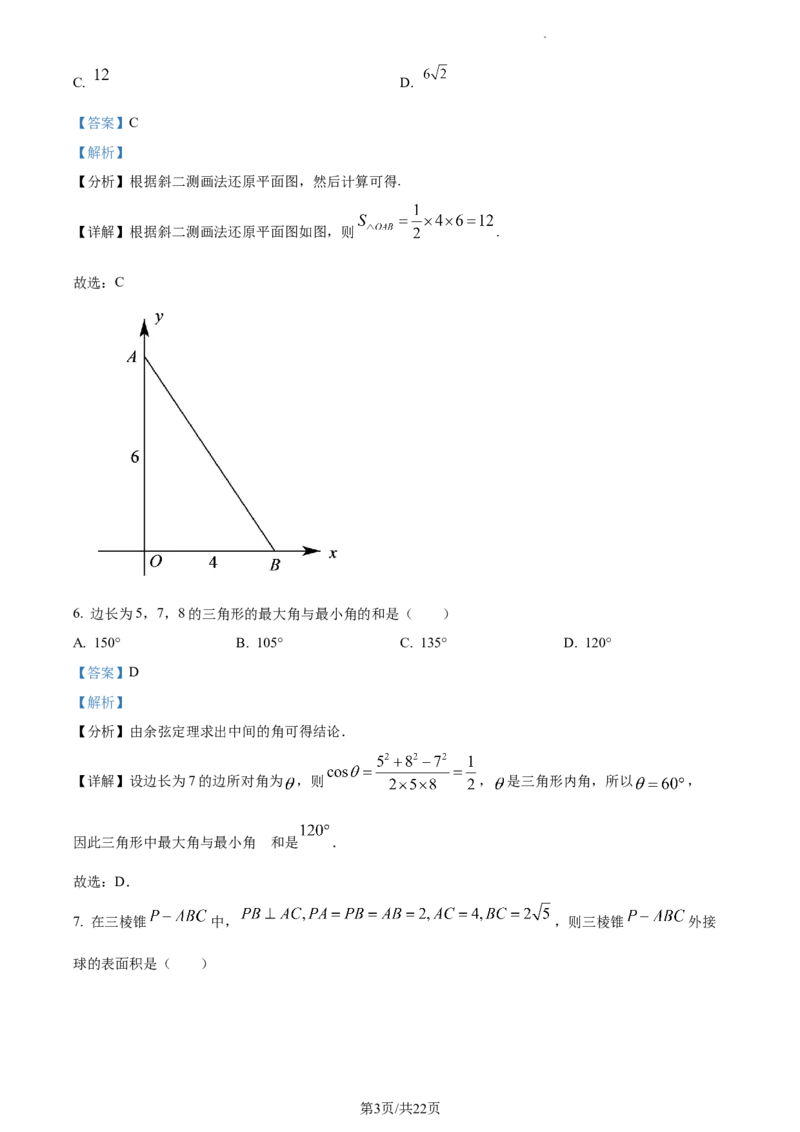
【分析】根据斜二测画法还原平面图,然后计算可得.
【详解】根据斜二测画法还原平面图如图,则 .
故选:C
6. 边长为5,7,8的三角形的最大角与最小角的和是( )
A. 150° B. 105° C. 135° D. 120°
【答案】D
【解析】
【分析】由余弦定理求出中间的角可得结论.
【详解】设边长为7的边所对角为 ,则 , 是三角形内角,所以 ,
的
因此三角形中最大角与最小角 和是 .
故选:D.
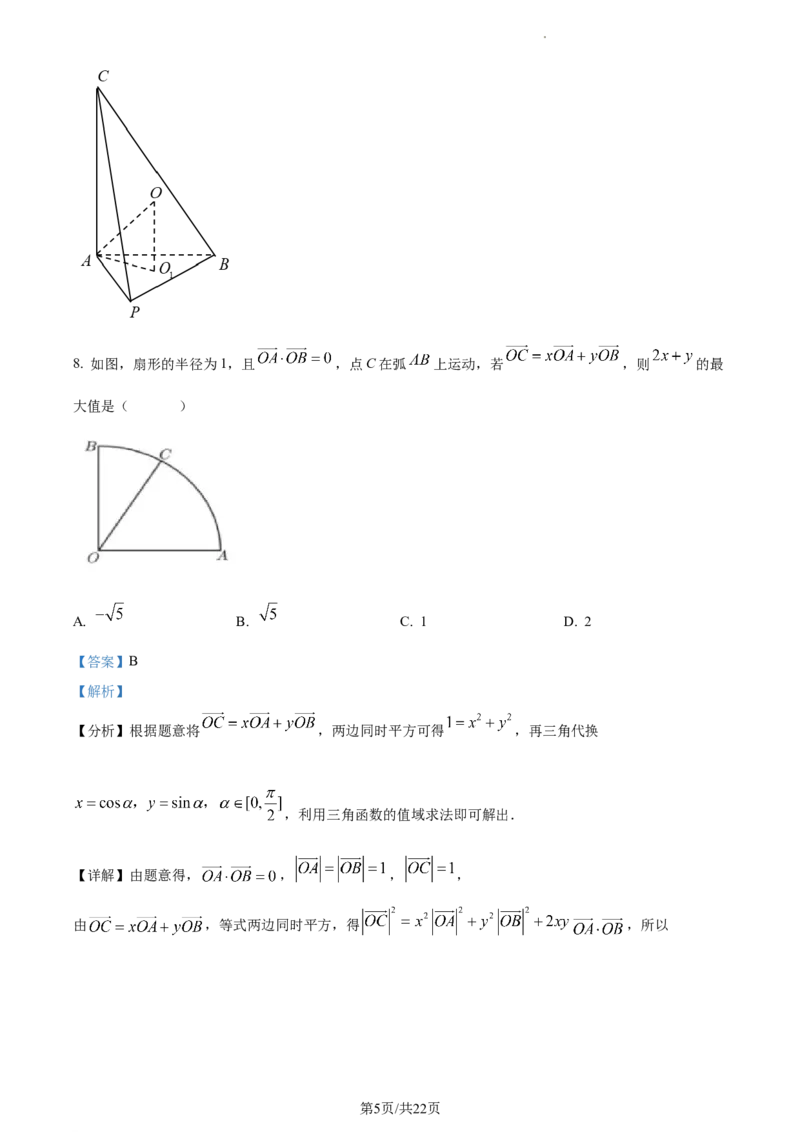
7. 在三棱锥 中, ,则三棱锥 外接
球的表面积是( )
第3页/共22页
学科网(北京)股份有限公司A. B. C. D.
【答案】B
【解析】
【分析】利用勾股定理证得 ,再根据线面垂直的判定定理可得 平面 ,故三棱锥
的外接球在过底面 外接圆圆心且垂直于底面 的直线上,利用正弦定理求得
外接圆的半径为 ,再根据三棱锥 外接球的半径为 求出外接球半径,即可得出答案.
【详解】解:由 ,
可得 ,所以 ,
又 ,且 , 平面 ,
所以 平面 ,
故三棱锥 的外接球在过底面 外接圆圆心且垂直于底面 的直线上,
由正弦定理,可得 外接圆的半径为 ,
所以三棱锥 外接球的半径为 ,
所以三棱锥 外接球的表面积为 ,
即三棱锥 外接球的表面积为 .
故选:B.
第4页/共22页
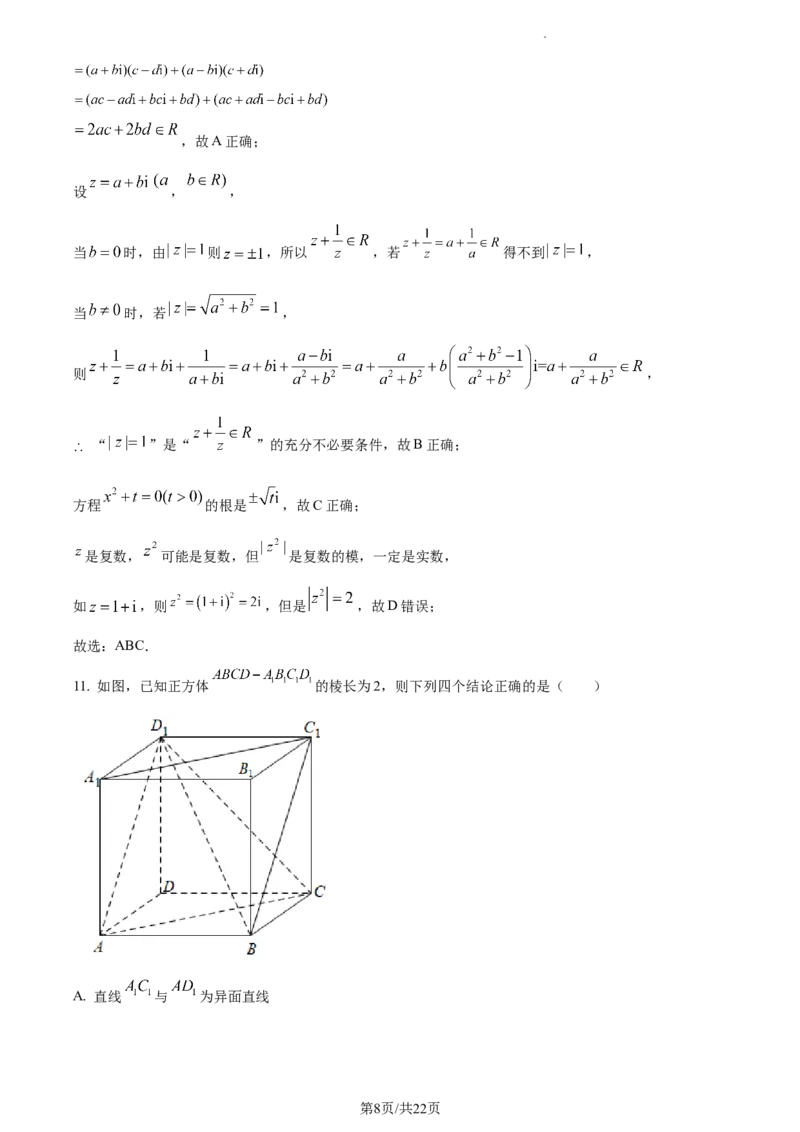
学科网(北京)股份有限公司8. 如图,扇形的半径为1,且 ,点C在弧 上运动,若 ,则 的最
大值是( )
A. B. C. 1 D. 2
【答案】B
【解析】
【分析】根据题意将 ,两边同时平方可得 ,再三角代换
,利用三角函数的值域求法即可解出.
【详解】由题意得, , , ,
由 ,等式两边同时平方,得 ,所以
第5页/共22页
学科网(北京)股份有限公司,令 ,则 ,
则 ,其中 ,因为
,所以 ,所以 ,即 的最大值为 .
故选:B.
二、多选题(选对得5分,选错得0分,选不全得2分)
9. 下列结论正确的有( )
A. 若存在实数 ,使得 ,则
B. 若 ,则若存在实数 ,使得
C. , 为非零向量,若 ,则 与 方向相同
D. 已知长度相等的三个非零向量 、 、 满足 ,则 是等边三角形.
【答案】ACD
【解析】
【分析】可以证明选项ACD正确,举反例说明选项B不正确,即得解.
【详解】A. 若存在实数 ,使得 ,则 , 所以该选项正确;
B. 若 ,则不一定存在实数 ,使得 ,如 是非零向量, 是零向量,则不存在实数 ,使
得 ,所以该选项不正确;
C. , 为非零向量,若 ,所以 ,所以
,则 与 方向相同,所以该选项正确;
第6页/共22页
学科网(北京)股份有限公司D. 已知长度相等的三个非零向量 、 、 满足 ,则 是等边三角形.如
图所示,设 中点为 ,连接 并延长到 ,使 连接 .显然四边形 是平行四
边形,因为 ,所以四边形 是菱形,因为 所以 ,所以
三点共线,所以 ,所以 同理 所以 ,所以 是等边
三角形.所以选项D正确.
故选:ACD
10. 在复数范围内,有下列命题,则其中真命题的有( )
A. 若 , 是两个复数,则 一定是实数
B. “ ”是“ ”的充分不必要条件
C. 方程 的根是
D.
【答案】ABC
【解析】
【分析】根据复数的运算以及和复数有关的定义分别判断即可.
【详解】解:设 , ,
则
第7页/共22页
学科网(北京)股份有限公司,故A正确;
设 , ,
当 时,由 则 ,所以 ,若 得不到 ,
当 时,若 ,
则 ,
“ ”是“ ”的充分不必要条件,故B正确;
方程 的根是 ,故C正确;
是复数, 可能是复数,但 是复数的模,一定是实数,
如 ,则 ,但是 ,故D错误;
故选:ABC.
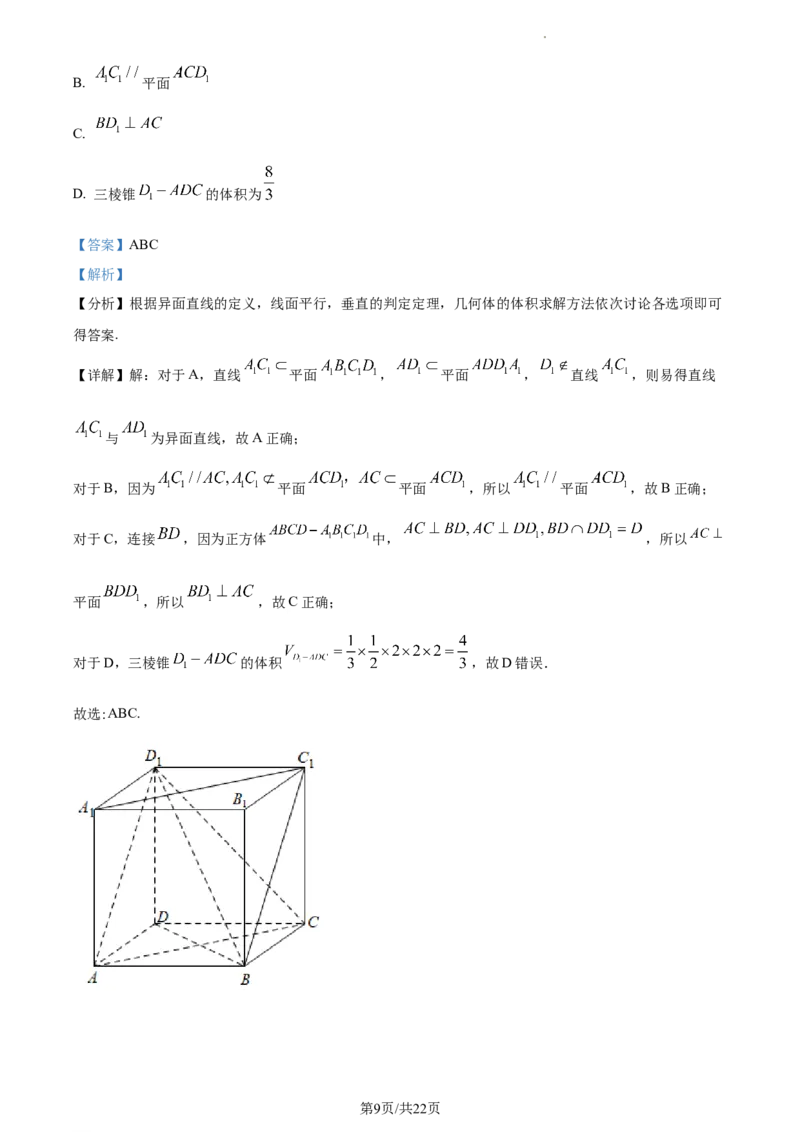
11. 如图,已知正方体 的棱长为2,则下列四个结论正确的是( )
A. 直线 与 为异面直线
第8页/共22页
学科网(北京)股份有限公司B. 平面
C.
D. 三棱锥 的体积为
【答案】ABC
【解析】
【分析】根据异面直线的定义,线面平行,垂直的判定定理,几何体的体积求解方法依次讨论各选项即可
得答案.
【详解】解:对于A,直线 平面 , 平面 , 直线 ,则易得直线
与 为异面直线,故A正确;
对于B,因为 平面 平面 ,所以 平面 ,故B正确;
对于C,连接 ,因为正方体 中, ,所以
平面 ,所以 ,故C正确;
对于D,三棱锥 的体积 ,故D错误.
故选:ABC.
第9页/共22页
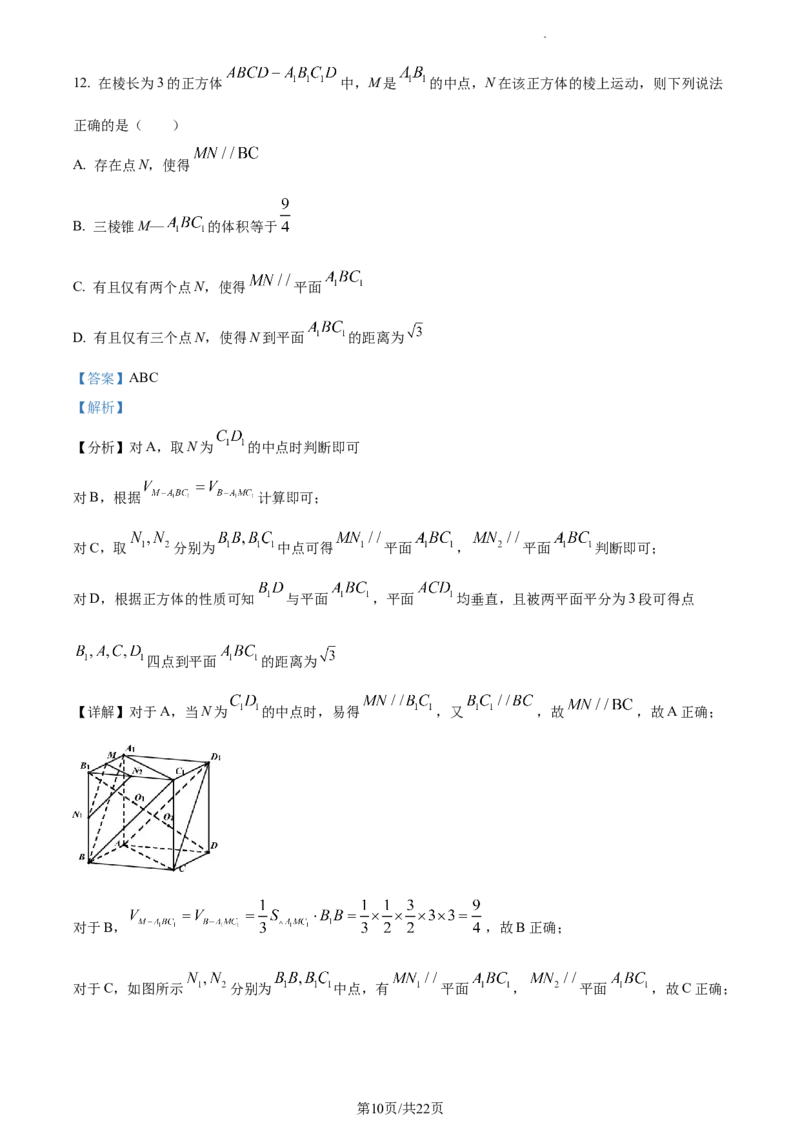
学科网(北京)股份有限公司12. 在棱长为3的正方体 中,M是 的中点,N在该正方体的棱上运动,则下列说法
正确的是( )
A. 存在点N,使得
B. 三棱锥M— 的体积等于
C. 有且仅有两个点N,使得 平面
D. 有且仅有三个点N,使得N到平面 的距离为
【答案】ABC
【解析】
【分析】对A,取N为 的中点时判断即可
对B,根据 计算即可;
对C,取 分别为 中点可得 平面 , 平面 判断即可;
对D,根据正方体的性质可知 与平面 ,平面 均垂直,且被两平面平分为3段可得点
四点到平面 的距离为
【详解】对于A,当N为 的中点时,易得 ,又 ,故 ,故A正确;
对于B, ,故B正确;
对于C,如图所示 分别为 中点,有 平面 , 平面 ,故C正确;
第10页/共22页
学科网(北京)股份有限公司对于D,易证 平面 , 平面 , 分别交平面 , 于 ,则
,所以有点 四点到平面 的距离为 ,故D错.
故选:ABC
三、填空题(做对得5分,做错得0分)
13. 已知向量 ,且 ,则 和 的值_________
【答案】
【解析】
【分析】由平面向量的坐标运算,代入可得: ,解方程即可得出答案.
【详解】因为 , ,所以
,所以 ,解得: .
故答案为:
14. 已知圆锥的高为 ,体积为 ,则以该圆锥的母线为半径的球的表面积为______________.
【答案】
【解析】
【分析】利用圆锥体积公式可求得圆锥底面半径 ,利用勾股定理可得母线长 ;根据球的表面积公式可求
得结果.
【详解】设圆锥的底面半径为 ,母线长为 ,
圆锥体积 , , ,
以 为半径的球的表面积 .
故答案为: .
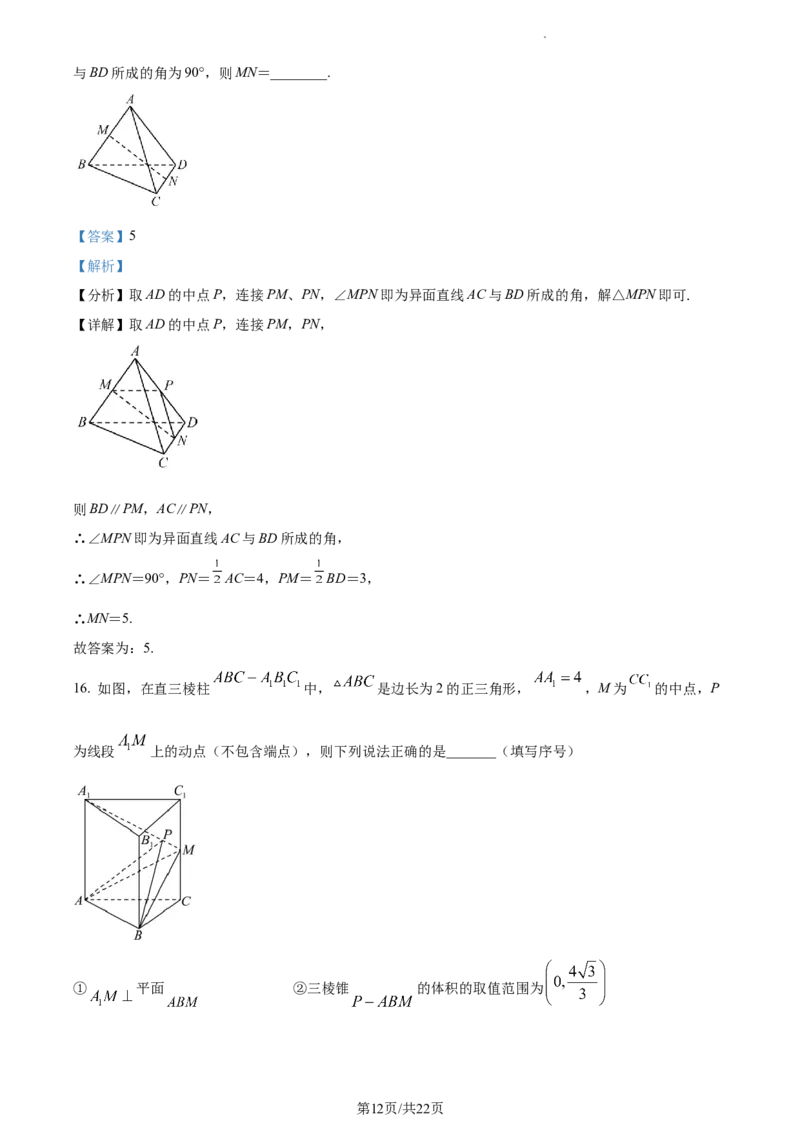
15. 如图,空间四边形ABCD的对角线AC=8,BD=6,M、N分别为AB、CD的中点,并且异面直线AC
第11页/共22页
学科网(北京)股份有限公司与BD所成的角为90°,则MN=________.
【答案】5
【解析】
【分析】取AD的中点P,连接PM、PN,∠MPN即为异面直线AC与BD所成的角,解△MPN即可.
【详解】取AD的中点P,连接PM,PN,
则BD∥PM,AC∥PN,
∴∠MPN即为异面直线AC与BD所成的角,
∴∠MPN=90°,PN= AC=4,PM= BD=3,
∴MN=5.
故答案为:5.
16. 如图,在直三棱柱 中, 是边长为2的正三角形, ,M为 的中点,P
为线段 上的动点(不包含端点),则下列说法正确的是_______(填写序号)
① 平面 ②三棱锥 的体积的取值范围为
第12页/共22页
学科网(北京)股份有限公司③ 与 为异面直线 ④存在点P,使得 与 垂直
【答案】②③
【解析】
【分析】由勾股定理求出 、 、 ,即可判断①,由 即可判断②,
根据异面直线的定义判断③,设 中点为N,即可得到 平面 ,即 平面 ,得出矛
盾,即可判断④;
【详解】解:由题意得 .则
, ,
所以 与 不垂直.故①错误;
,点B到平面 的距离为 ,
由 ,所以 ,所以 ,
又 ,则 ,
故②正确;
的
P为线段 上 点(不包括端点),故 与 为异面直线,故③正确;
为
若 ,设 中点 N,所以 ,又平面 平面 ,
平面 平面 , 平面 ,
所以 平面 , 平面 ,所以 ,
又 ,则 平面 ,即 平面 ,
又因为 平面 ,故点P与点 重合,不合题意,故④错误.
第13页/共22页
学科网(北京)股份有限公司故答案为:②③
四、解答题
17. 如图为长方体与半球拼接的组合体,已知长方体的长、宽、高分别为10,8,15(单位:cm),球的
直径为5 cm,求该组合体的体积和表面积
【答案】体积为1200+ (cm3),表面积700+ (cm2).
【解析】
【分析】利用长方体和球的体积公式、表面积公式进行求解即可.
【详解】根据该组合体是由一个长方体和一个半球组合而成.由已知可得
V =10×8×15=1200(cm3),
长方体
又V = ,
半球
所以所求几何体体积为:
V=V +V =1200+ (cm3).
长方体 半球
因为S =2×(10×8+8×15+10×15)=700(cm2),
长方体全
第14页/共22页
学科网(北京)股份有限公司故所求几何体的表面积S =S +S -S
表面积 长方体全 半球 半球底
=700+
=700+ (cm2).
18. 已知向量 .
(1)若 ,求 ;
(2)若向量 与 的夹角是钝角,求实数k的取值范围.
【答案】(1) ;
(2) 且 .
【解析】
【分析】(1)根据向量共线的坐标表示即可求出k,根据向量模长公式即可计算;
(2)若向量 与 的夹角是钝角,则 <0且 与 不反向,根据数量积即可运算.
【小问1详解】
∵ ,
∴ ,解得 ,
∴ .
【小问2详解】
∵ 与 的夹角是钝角,
∴ ,且 与 不反向,
即 且 ,
第15页/共22页
学科网(北京)股份有限公司∴ 且 .
19. 已知复数 和它的共轭复数 满足 .
(1)求z;
(2)若z是关于x的方程 的一个根,求复数 的模.
【答案】(1)
(2)1
【解析】
【分析】(1)设 ,根据复数代数形式的运算法则及复数相等的充要条件得到方程组,
解得即可;
(2)将 代入已知方程,利用复数代数形式的乘法运算及复数为 的充要条件得到方程,即可求
出 、 ,再代入 ,利用复数除法运算法则化简,从而求出其模;
【小问1详解】
解:设 ,则 ,
所以 ,
所以 ,即 ,所以 ;
【小问2详解】
解:将 代入已知方程可得 ,
即 ,整理可得 ,
所以 ,解得 ,
第16页/共22页
学科网(北京)股份有限公司所以 ,又 ,
故复数 的模为1.
20. 已知 的内角 、 、 的对边分别是 、 、 ,且 .
(1)求 ;
(2)若 ,求 的面积的最大值.
【答案】(1) ;
(2) .
【解析】
【分析】(1)利用正弦定理边化角,再利用和角的正弦化简求解作答.
(2)利用余弦定理结合均值不等式求出 的最大值,再由面积定理求解作答.
【小问1详解】
在 中, ,由 及正弦定理得: ,
即 , ,
于是得 ,又 ,即 ,则 ,因 ,
所以 .
【小问2详解】
,由余弦定理得: ,当且仅当 时取“=”,
因此, ,于是得 ,当且仅当 时取“=”,
第17页/共22页
学科网(北京)股份有限公司所以 的面积的最大值为 .
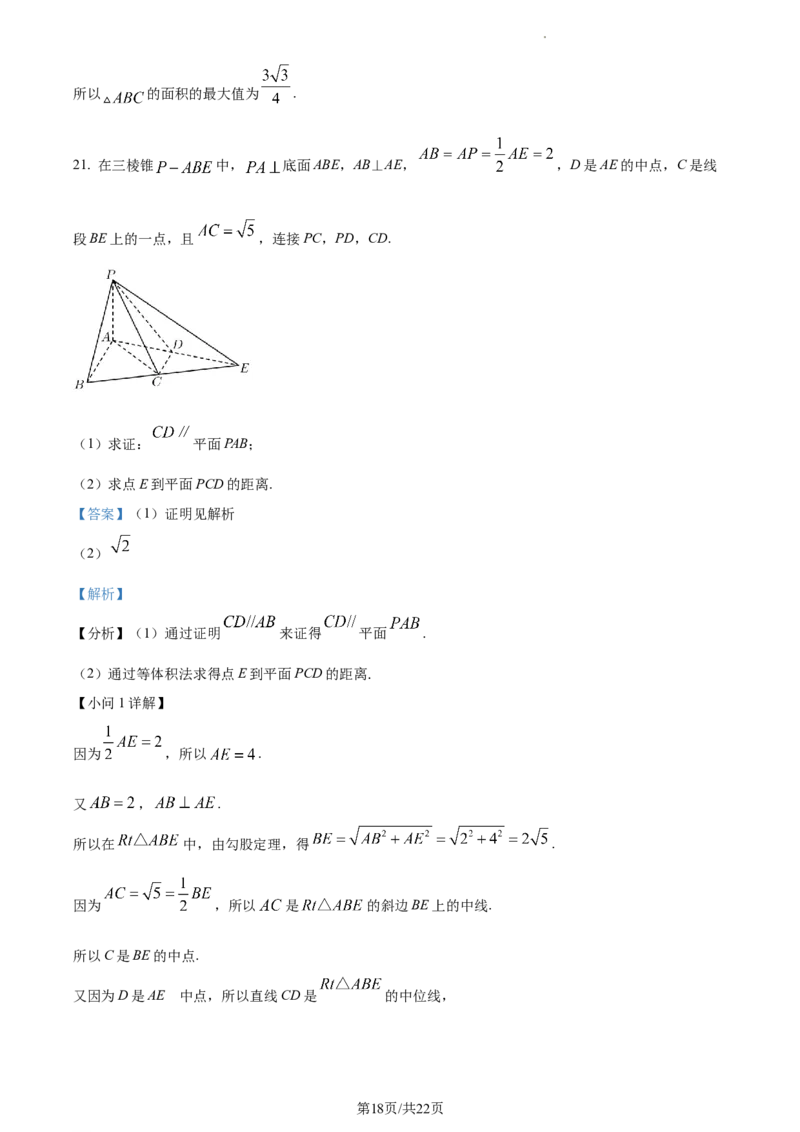
21. 在三棱锥 中, 底面ABE,AB⊥AE, ,D是AE的中点,C是线
段BE上的一点,且 ,连接PC,PD,CD.
(1)求证: 平面PAB;
(2)求点E到平面PCD的距离.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)通过证明 来证得 平面 .
(2)通过等体积法求得点E到平面PCD的距离.
【小问1详解】
因为 ,所以 .
又 , .
所以在 中,由勾股定理,得 .
因为 ,所以 是 的斜边BE上的中线.
所以C是BE的中点.
的
又因为D是AE 中点,所以直线CD是 的中位线,
第18页/共22页
学科网(北京)股份有限公司所以 .
又因为 平面PAB, 平面PAB,所以 平面PAB.
【小问2详解】
由(1)得, .
又因为 , .
所以 .
又因为 ,所以 .
由题意得 ,且 ,所以 .
设点E到平面PCD的距离为d,则由
得 ,即 ,解得 .
故点E到平面PCD的距离为 .
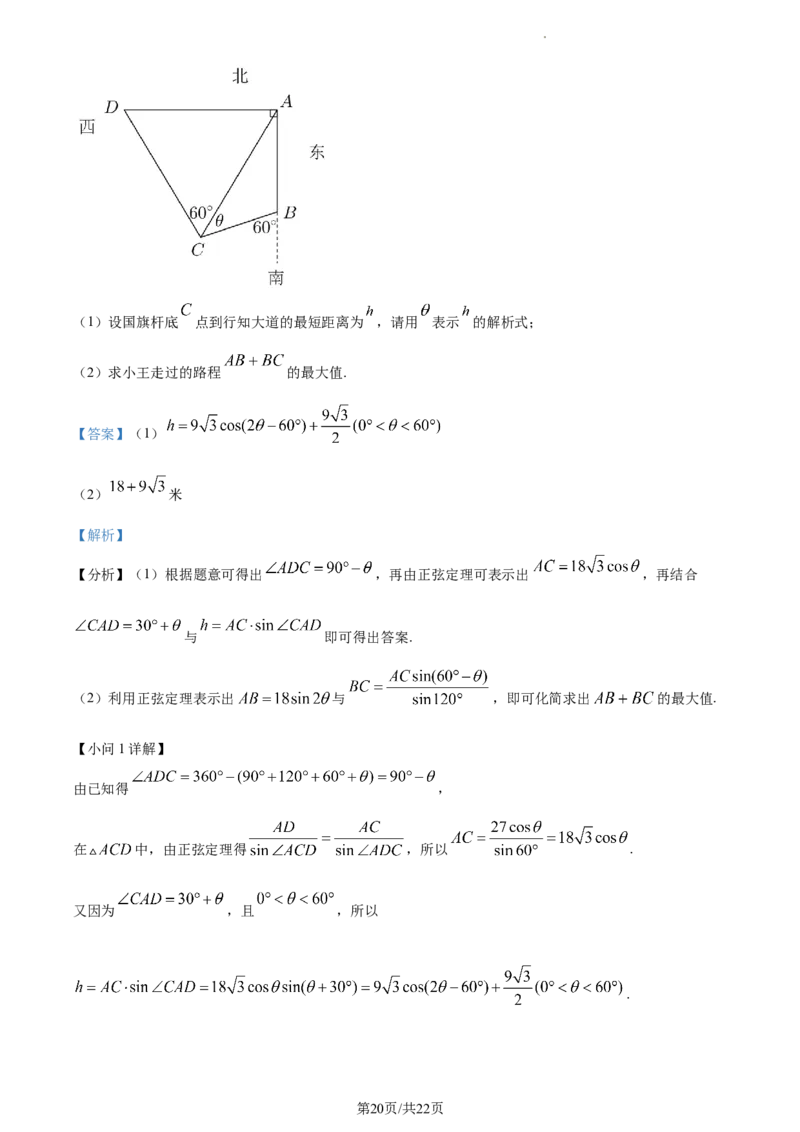
22. 重庆育才中学学生小王和小李星期天一同返校进入校门,如图所示,背对着校门站在陶行知雕像前
点,小李沿着行知大道(正西方向)走27米后到达 点.小王以垂直于小李的路线向正南方向行走若干米
后到达陶行知纪念馆 点,后又沿着南偏西 的方向行走到达国旗杆下 点,经过测量发现
.设 ,如图所示.
第19页/共22页
学科网(北京)股份有限公司(1)设国旗杆底 点到行知大道的最短距离为 ,请用 表示 的解析式;
(2)求小王走过的路程 的最大值.
【答案】(1)
(2) 米
【解析】
【分析】(1)根据题意可得出 ,再由正弦定理可表示出 ,再结合
与 即可得出答案.
(2)利用正弦定理表示出 与 ,即可化简求出 的最大值.
【小问1详解】
由已知得 ,
在 中,由正弦定理得 ,所以 .
又因为 ,且 ,所以
.
第20页/共22页
学科网(北京)股份有限公司【小问2详解】
在 中,由正弦定理得 ,
,
于是 .
因为 ,所以当 时, 取得最大值 米.
第21页/共22页
学科网(北京)股份有限公司第22页/共22页
学科网(北京)股份有限公司