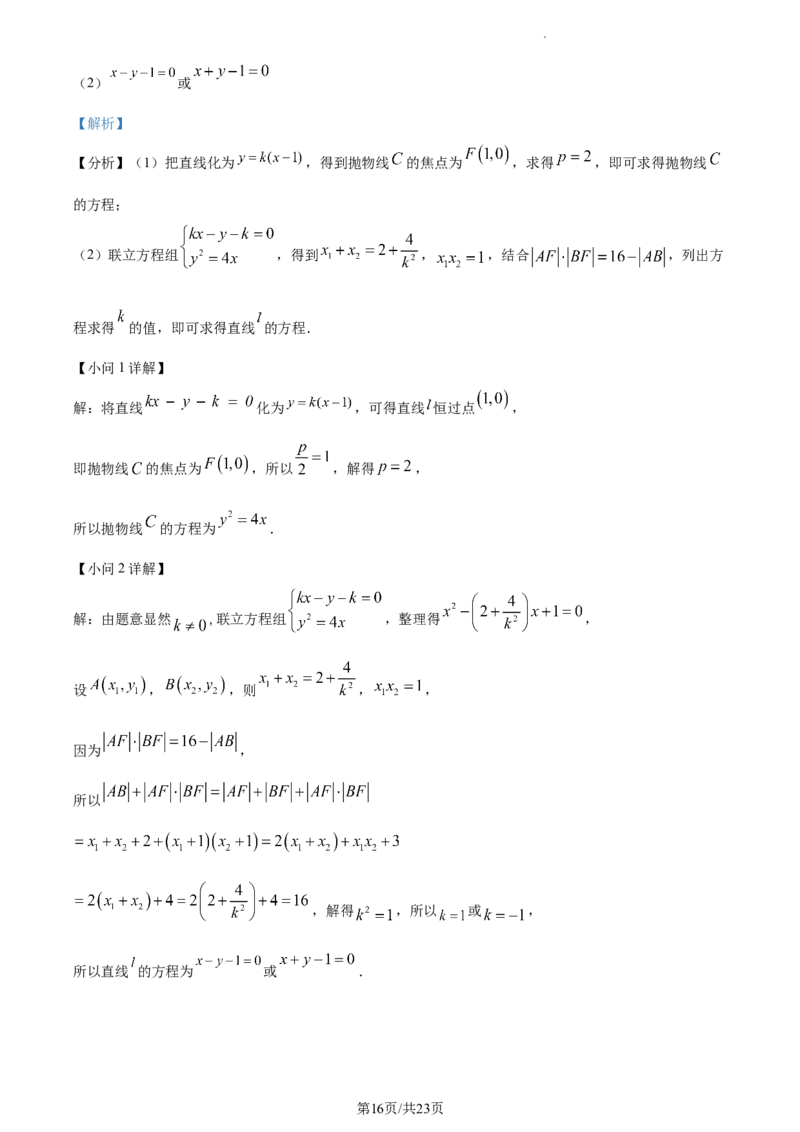文档内容
第一学期期末调研测试卷
高二数学
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 已知直线m经过 , 两点,则直线m的斜率为( )
A. -2 B. C. D. 2
【答案】A
【解析】
【分析】根据斜率公式求得正确答案.
【详解】直线 的斜率为: .
故选:A
2. 已知数列 满足 , ,则 ( )
A. B. C. 1 D. 2
【答案】C
【解析】
【分析】结合递推关系式依次求得 的值.
【详解】因为 , ,
所以 ,得 .
由 ,得 .
故选:C
第1页/共23页
学科网(北京)股份有限公司3. 抛物线型太阳灶是利用太阳能辐射的一种装置.当旋转抛物面的主光轴指向太阳的时候,平行的太阳光
线入射到旋转抛物面表面,经过反光材料的反射,这些反射光线都从它的焦点处通过,形成太阳光线的高
密集区,抛物面的焦点在它的主光轴上.如图所示的太阳灶中,灶深CD即焦点到灶底(抛物线的顶点)
的距离为1m,则灶口直径AB为( )
A. 2m B. 3m C. 4m D. 5m
【答案】C
【解析】
【分析】建立如图所示的平面直角坐标系,设抛物线的方程为 ,根据 是抛物线
的焦点,求得抛物线的方程 ,进而求得 的长.
【详解】由题意,建立如图所示的平面直角坐标系,O与C重合,
设抛物线的方程为 ,
由题意可得 是抛物线的焦点,即 ,可得 ,
所以抛物线的方程为 ,
当 时, ,所以 .
故选:C.
第2页/共23页
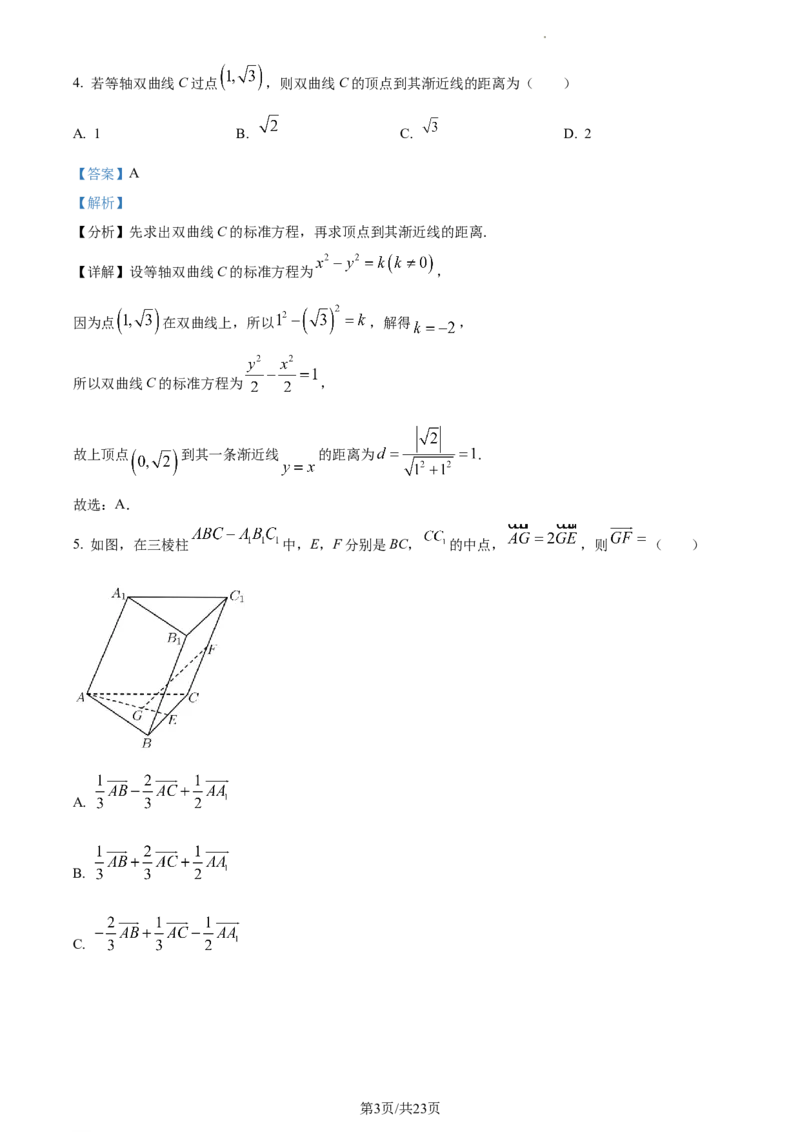
学科网(北京)股份有限公司4. 若等轴双曲线C过点 ,则双曲线C的顶点到其渐近线的距离为( )
A. 1 B. C. D. 2
【答案】A
【解析】
【分析】先求出双曲线C的标准方程,再求顶点到其渐近线的距离.
【详解】设等轴双曲线C的标准方程为 ,
因为点 在双曲线上,所以 ,解得 ,
所以双曲线C的标准方程为 ,
故上顶点 到其一条渐近线 的距离为 .
故选:A.
5. 如图,在三棱柱 中,E,F分别是BC, 的中点, ,则 ( )
A.
B.
C.
第3页/共23页
学科网(北京)股份有限公司D.
【答案】D
【解析】
的
【分析】根据空间向量线性运算 几何意义进行求解即可.
【详解】
,
故选:D.
6. 已知在空间直角坐标系 (O为坐标原点)中,点 关于x轴的对称点为点B,则z轴与平
面OAB所成的线面角为( )
A. B. C. D.
【答案】B
【解析】
【分析】根据点关于坐标轴对称的性质,结合空间向量夹角公式进行求解即可.
【详解】因为点 关于x轴的对称点为 ,
所以 , .
设平面OAB的一个法向量为 ,则 得 所以 ,
令 ,得 ,所以 .
又z轴的一个方向向量为 ,设z轴与平面OAB所成的线面角为 ,
则 ,
第4页/共23页
学科网(北京)股份有限公司所以所求的线面角为 ,
故选:B.
7. 若圆C: 上有到 的距离为1的点,则实数m的取值范围为( )
A. B.
C. D.
【答案】C
【解析】
【分析】利用圆与圆的位置关系进行求解即可.
【详解】将圆C的方程化为标准方程得 ,
所以 .因为圆C上有到 的距离为1的点,
所以圆C与圆 : 有公共点,所以 .
因为 ,所以 ,
解得 ,
故选:C.
8. 南宋数学家杨辉在《详解九章算法》中讨论过高阶等差数列与一般等差数列不同,前后两项之差并不相
等,而是逐项差数之差或者高次差相等.例如“百层球堆垛”:第一层有1个球 ,第二层有3个球
,第三层有6个球 ,第四层有10个球 ,第五层有15个球 ,…,各层
球数之差 : , , , ,…即2,3, 4,5,…是等差数列.现有一个
高阶等差数列,其前6项分别为1,3,6,12,23,41,则该数列的第8项为( ).
A. 51 B. 68 C. 106 D. 157
【答案】C
【解析】
第5页/共23页
学科网(北京)股份有限公司【分析】对高阶等差数列按其定义逐一进行构造数列 ,直到出现一般等差数列为止,再根据其递
推关系进行求解.
【详解】现有一个高阶等差数列,其前6项分别为1,3,6,12,23,41,
各项与前一项之差 : , , , , ,…
即2,3,6,11,18,…,
, , , ,…
即1,3,5,7,…是等差数列,
所以 , .
故选:C.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符
合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
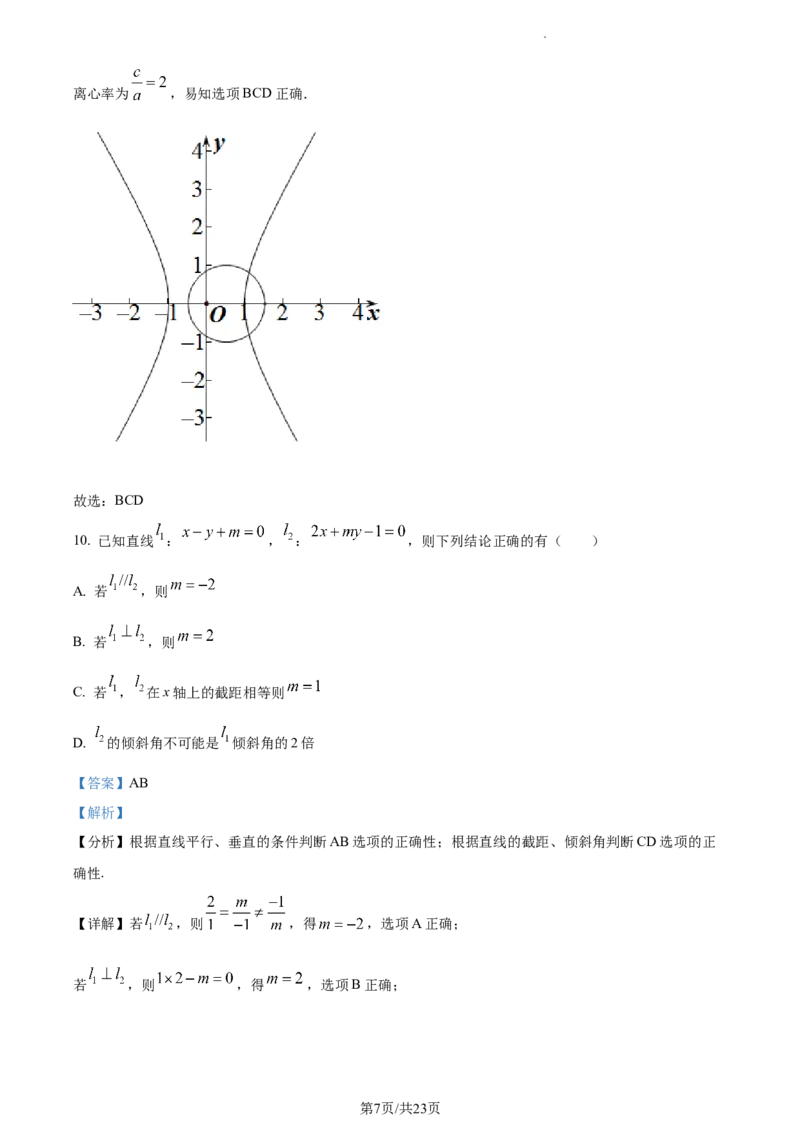
9. 已知双曲线C: ,则( )
A. 双曲线C与圆 有3个公共点
B. 双曲线C的离心率与椭圆 的离心率的乘积为1
C. 双曲线C与双曲线 有相同的渐近线
D. 双曲线C的一个焦点与抛物线 的焦点相同
【答案】BCD
【解析】
【分析】由圆锥曲线的几何性质直接可得.
【详解】解:作图可知A不正确;由已知得双曲线C中, , , ,所以双曲
线C的焦点为 ,顶点为 ,渐近线方程为 ,
第6页/共23页
学科网(北京)股份有限公司离心率为 ,易知选项BCD正确.
故选:BCD
10. 已知直线 : , : ,则下列结论正确的有( )
A. 若 ,则
B. 若 ,则
C. 若 , 在x轴上的截距相等则
D. 的倾斜角不可能是 倾斜角的2倍
【答案】AB
【解析】
【分析】根据直线平行、垂直的条件判断AB选项的正确性;根据直线的截距、倾斜角判断CD选项的正
确性.
【详解】若 ,则 ,得 ,选项A正确;
若 ,则 ,得 ,选项B正确;
第7页/共23页
学科网(北京)股份有限公司若 , 在x轴上的截距相等,则 ,解得 ,选项C错误;
当 时, 的倾斜角 恰好是 的倾斜角 的2倍,选项D错误.
故选:AB
【点睛】解决此题的关键是要弄清楚直线的点斜式和直线的一般式判断两直线平行和垂直的充要条件,其
次还要注意斜率的存在性,一定要注意分类讨论.易错点:两直线平行一定要注意纵截距不等和斜率的存
在性.
11. 记数列 的前n项和为 ,则下列条件中一定能得出 是等比数列的有( )
A. B.
C. D.
【答案】BC
【解析】
【分析】应用特殊数列,令数列 为 的常数列即可判断A、D;利用 关系求得 、
即可判断B;由对数的运算性质有 ,结合等比中项性质判断C.
【详解】当 为常数列且 时, 、 都成立,但不是等比数列,A、D不符
合要求;
B:由 ,则 ;当 时, ,即 ,故 是
首项为1,公比为2的等比数列;
C:由 ,即 且 ,故 是等比数列;
故选:BC
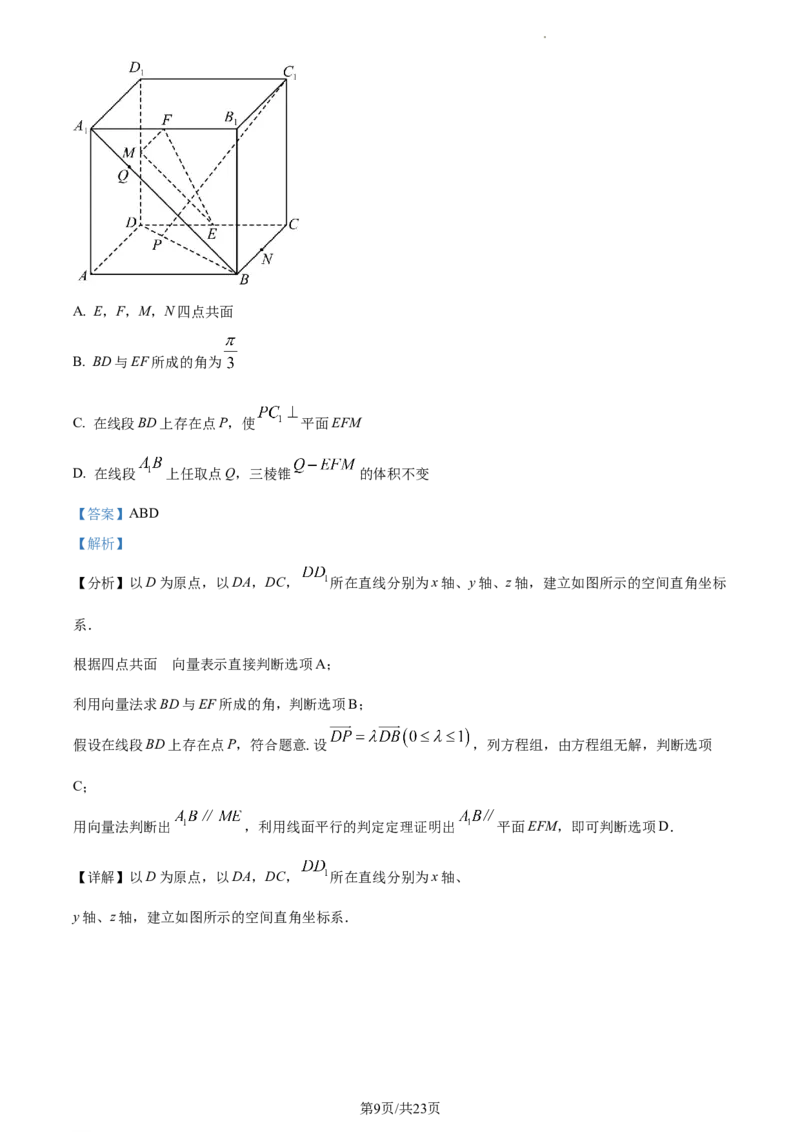
12. 如图,已知正方体 中,E,F,M,N分别是CD, , ,BC的中点,则下列
说法正确的有( )
第8页/共23页
学科网(北京)股份有限公司A. E,F,M,N四点共面
B. BD与EF所成的角为
C. 在线段BD上存在点P,使 平面EFM
D. 在线段 上任取点Q,三棱锥 的体积不变
【答案】ABD
【解析】
【分析】以D为原点,以DA,DC, 所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标
系.
的
根据四点共面 向量表示直接判断选项A;
利用向量法求BD与EF所成的角,判断选项B;
假设在线段BD上存在点P,符合题意.设 ,列方程组,由方程组无解,判断选项
C;
用向量法判断出 ,利用线面平行的判定定理证明出 平面EFM,即可判断选项D.
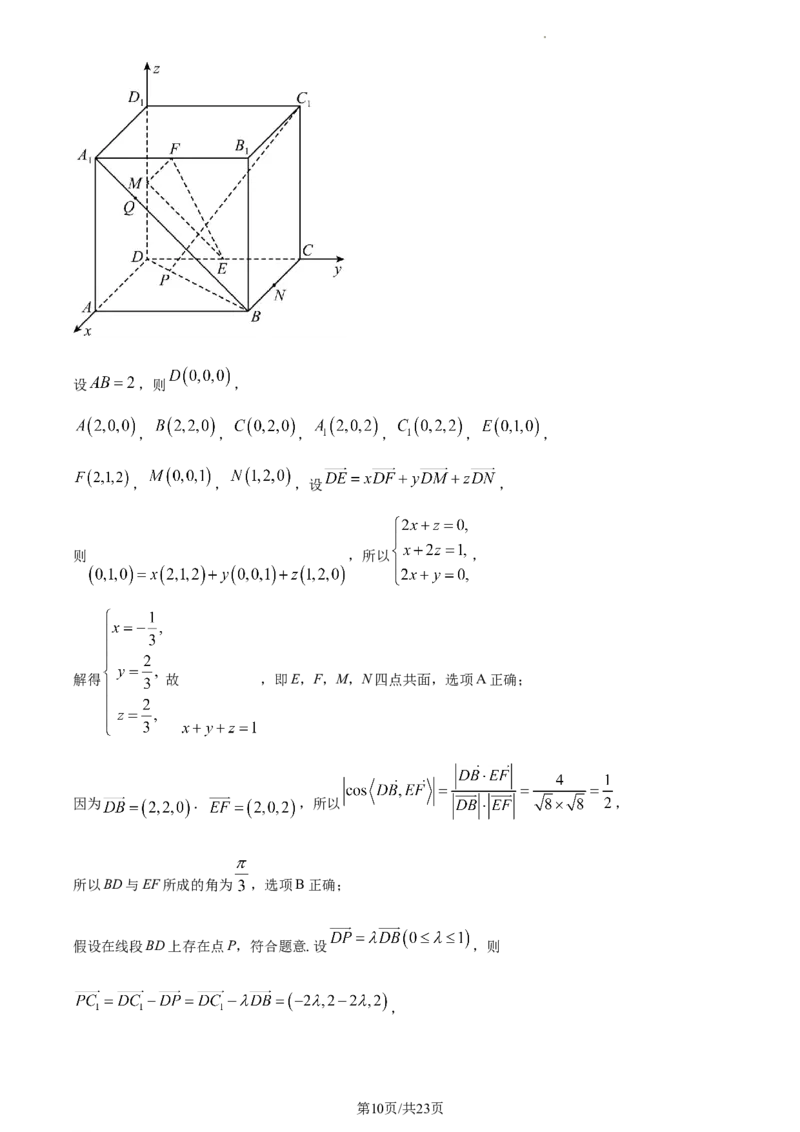
【详解】以D为原点,以DA,DC, 所在直线分别为x轴、
y轴、z轴,建立如图所示的空间直角坐标系.
第9页/共23页
学科网(北京)股份有限公司设 ,则 ,
, , , , , ,
, , ,设 ,
则 ,所以 ,
解得 故 ,即E,F,M,N四点共面,选项A正确;
因为 . ,所以 ,
所以BD与EF所成的角为 ,选项B正确;
假设在线段BD上存在点P,符合题意.设 ,则
,
第10页/共23页
学科网(北京)股份有限公司若 平面EFM,则 , .
因为 , ,所以 ,
此方程组无解,所以在线段BD上不存在点P,使 平面EFM,选项C错误;
因为 ,所以 ,
又 平面EFM, 平面EFM,所以 平面EFM,
故 上的所有点到平面EFM的距离均相等,即在线段 上任取点Q,
的
三棱锥 体积不变,选项D正确.
故选:ABD
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知向量 , ,若 ,则 ______.
【答案】
【解析】
【分析】根据向量平行求得 ,由此求得 .
【详解】由于 ,所以 .
故答案为:
14. 已知等差数列 满足 ,请写出一个符合条件的通项公式 ______.
【答案】3(答案不唯一)
【解析】
【分析】由已知条件结合等差数列的性质可得 ,则 ,从而可写出数列的一个通项公式
【详解】因为 是等差数列,且 ,所以 , .
当公差为0时, ;公差为1时, ;…
故答案为:3(答案为唯一)
第11页/共23页
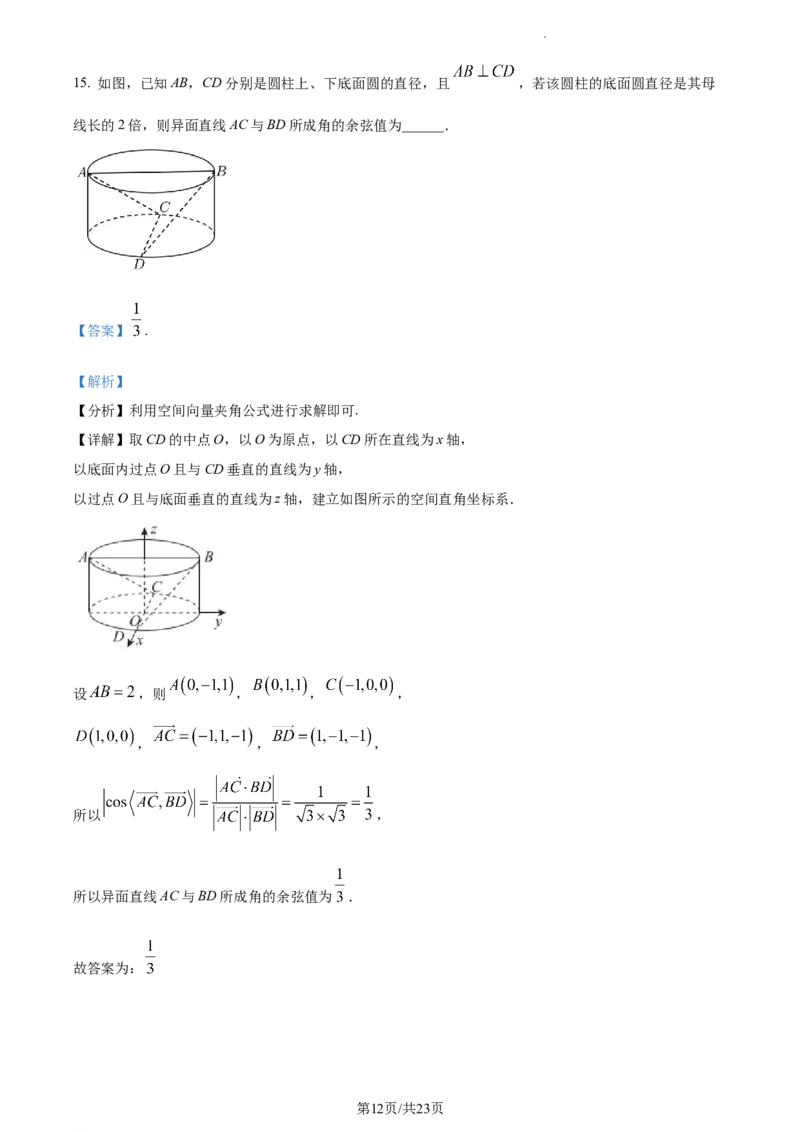
学科网(北京)股份有限公司15. 如图,已知AB,CD分别是圆柱上、下底面圆的直径,且 ,若该圆柱的底面圆直径是其母
线长的2倍,则异面直线AC与BD所成角的余弦值为______.
【答案】 .
【解析】
【分析】利用空间向量夹角公式进行求解即可.
【详解】取CD的中点O,以O为原点,以CD所在直线为x轴,
以底面内过点O且与CD垂直的直线为y轴,
以过点O且与底面垂直的直线为z轴,建立如图所示的空间直角坐标系.
设 ,则 , , ,
, , ,
所以 ,
所以异面直线AC与BD所成角的余弦值为 .
故答案为:
第12页/共23页
学科网(北京)股份有限公司16. 已知过椭圆 上的动点 作圆 ( 为圆心): 的两条切线,
切点分别为 ,若 的最小值为 ,则椭圆 的离心率为______.
【答案】
【解析】
【分析】由椭圆方程和圆的方程可确定椭圆焦点、圆心和半径;当 最小时,可知 ,此
时 ;根据椭圆性质知 ,解方程可求得 ,进而得到离心率.
【详解】由椭圆 方程知其右焦点为 ;由圆 的方程知:圆心为 ,半径为 ;
当 最小时,则 最小,即 ,此时 最小;
此时 , ;
为椭圆右顶点时, ,解得: ,
椭圆 的离心率 .
故答案为: .
第13页/共23页
学科网(北京)股份有限公司四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知圆C: 的半径为1.
(1)求实数a的值;
(2)判断直线l: 与圆C是否相交?若不相交,请说明理由;若相交,请求出弦长.
【答案】(1) ;
(2)直线l与圆C相交, .
【解析】
【分析】(1)利用配方法进行求解即可;
(2)根据点到直线的距离公式,结合圆的弦长公式进行求解即可.
【小问1详解】
将 化为标准方程得:
.
因为圆C的半径为1,所以 ,得 .
【小问2详解】
由(1)知圆C的圆心为 ,半径为1.
设圆心C到直线l的距离为d,则 ,
所以直线l与圆C相交,设其交点为A,B,则 ,即 .
18. 已知等比数列 满足 .
(1)求 的通项公式;
(2)记 的前n项和为 ,证明: , , 成等差数列.
【答案】(1)
第14页/共23页
学科网(北京)股份有限公司(2)证明见解析
【解析】
【分析】(1)设等比数列 的公比为 ,根据 ,求得 的值,即可求得数列 的通
项公式;
(2)由等比数列的求和公式求得 ,得到 , ,化简得到
,即可求解.
【小问1详解】
解:设等比数列 的公比为 ,
因为 ,所以 ,解得 ,
所以 ,
所以数列 的通项公式 .
【小问2详解】
解:由(1)可得 ,
, ,
所以 ,
所以 ,即 , , 成等差数列.
19. 已知直线 恒过抛物线 的焦点F.
(1)求抛物线 的方程;
(2)若直线 与抛物线 交于A,B两点,且 ,求直线 的方程.
【答案】(1)
第15页/共23页
学科网(北京)股份有限公司(2) 或
【解析】
【分析】(1)把直线化为 ,得到抛物线 的焦点为 ,求得 ,即可求得抛物线
的方程;
(2)联立方程组 ,得到 , ,结合 ,列出方
程求得 的值,即可求得直线 的方程.
【小问1详解】
解:将直线 化为 ,可得直线 恒过点 ,
即抛物线 的焦点为 ,所以 ,解得 ,
所以抛物线 的方程为 .
【小问2详解】
解:由题意显然 ,联立方程组 ,整理得 ,
设 , ,则 , ,
因为 ,
所以
,解得 ,所以 或 ,
所以直线 的方程为 或 .
第16页/共23页
学科网(北京)股份有限公司20. 已知数列 满足 .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
【答案】(1)
(2)
【解析】
【分析】(1)当 时,由 ,可得 ,两式
相减化简可求得通项,
(2)由(1)得 ,然后利用裂项相消法可求得结果
【小问1详解】
因为 ,
所以 时,
,
两式作差得, ,
所以 时, ,
又 时, ,得 ,符合上式,
第17页/共23页
学科网(北京)股份有限公司所以 的通项公式为 .
【小问2详解】
由(1)知 ,
所以
.
即数列 的前n项和 .
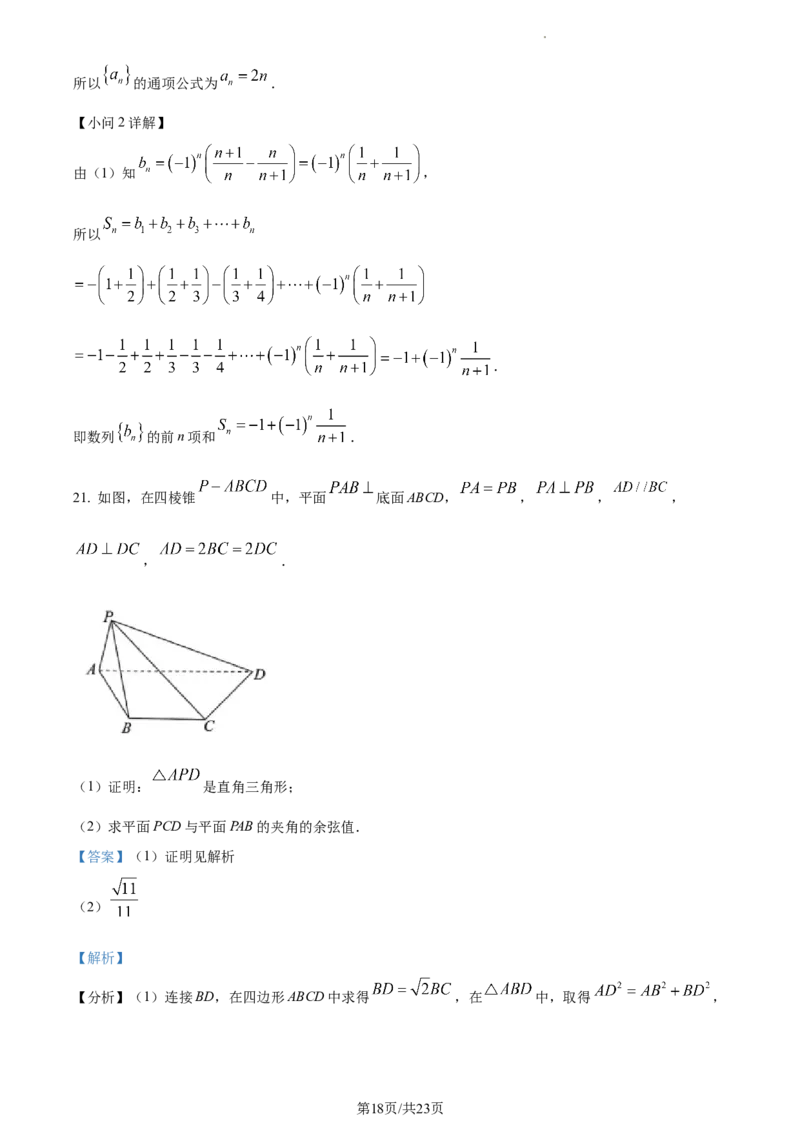
21. 如图,在四棱锥 中,平面 底面ABCD, , , ,
, .
(1)证明: 是直角三角形;
(2)求平面PCD与平面PAB的夹角的余弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)连接BD,在四边形ABCD中求得 ,在 中,取得 ,
第18页/共23页
学科网(北京)股份有限公司得到 ,由线面垂直的性质证得 平面 ,得到 ,再由线面垂直的判定定理,证
得 平面PBD,进而得到 ,即可证得 是直角三角形.
(2)以 为原点,以 所在直线为x轴,过点 且与 平行的直线为y轴, 所在直线为z轴,建
立的空间直角坐标系,分别求得平面 和平面 的法向量,利用向量的夹角公式,即可求解.
【小问1详解】
证明:如图所示,连接BD,
为
因 四边形 中,可得 , , ,
所以 , ,则 .
在 中,由余弦定理可得 ,所以 ,所以 .
因为平面 底面 ,平面 底面 ,
底面ABCD,所以 平面PAB,
因为 平面PAB,所以 ,
因为 , ,所以 平面PBD.
因为 平面PBD,所以 ,即 是直角三角形.
【小问2详解】
解:由(1)知 平面PAB,取AB的中点O,连接PO,
因为 ,所以 ,
因为 平面 ,平面 底面 ,平面 底面 ,
所以 底面 ,
以 为原点,以 所在直线为x轴,过点 且与 平行的直线为y轴, 所在直线为z轴,建立如图
所示的空间直角坐标系,
第19页/共23页
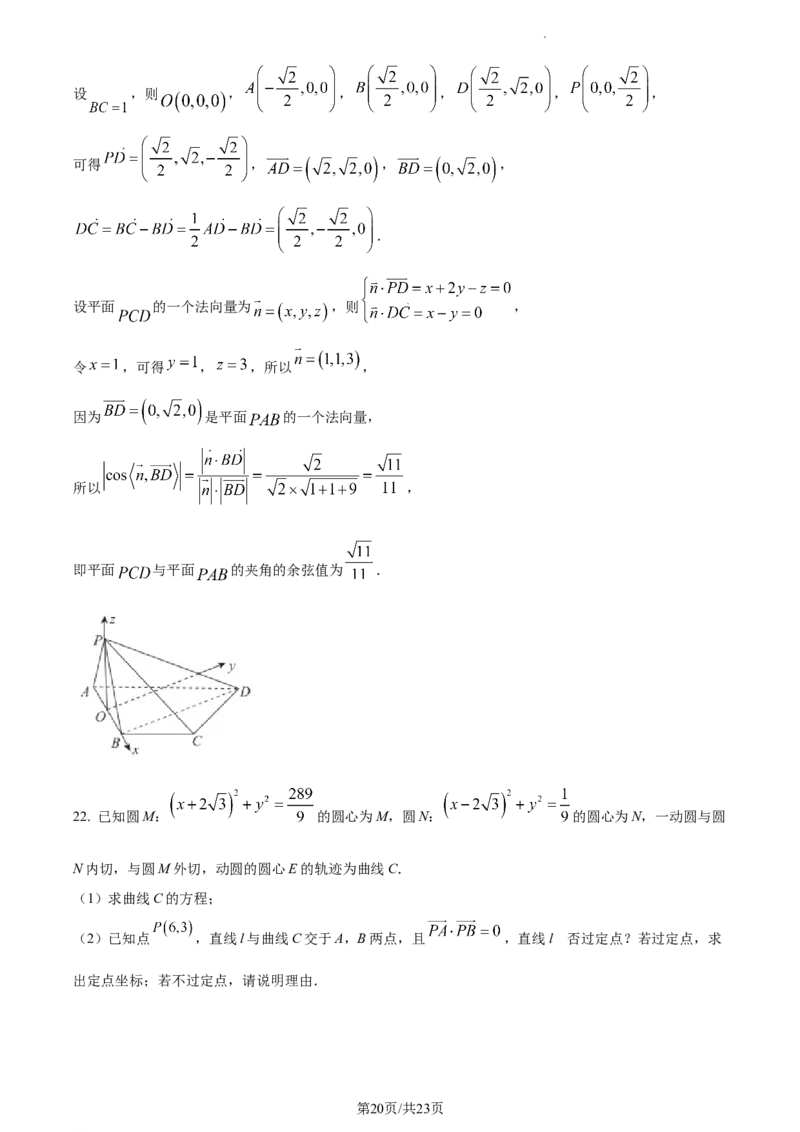
学科网(北京)股份有限公司设 ,则 , , , , ,
可得 , , ,
.
设平面 的一个法向量为 ,则 ,
令 ,可得 , ,所以 ,
因为 是平面 的一个法向量,
所以 ,
即平面 与平面 的夹角的余弦值为 .
22. 已知圆M: 的圆心为M,圆N: 的圆心为N,一动圆与圆
N内切,与圆M外切,动圆的圆心E的轨迹为曲线C.
(1)求曲线C的方程;
是
(2)已知点 ,直线l与曲线C交于A,B两点,且 ,直线l 否过定点?若过定点,求
出定点坐标;若不过定点,请说明理由.
第20页/共23页
学科网(北京)股份有限公司【答案】(1) , ;
(2)过, .
【解析】
【分析】(1)根据两圆内切和外切的性质,结合双曲线的定义进行求解即可;
(2)设出直线l的方程与双曲线的方程联立,利用一元二次方程根与系数关系,结合平面向量数量积的坐
标表示公式进行求解判断即可.
【小问1详解】
设圆E的圆心为 ,半径为r,
则 , ,所以 .
由双曲线定义可知,E的轨迹是以M,N为焦点、实轴长为6的双曲线的右支,
所以动圆的圆心E的轨迹方程为 , ;
【小问2详解】
设 , ,直线l的方程为 .
由 得 ,且 ,
故 又 ,所以 .
又 , ,
所以
第21页/共23页
学科网(北京)股份有限公司,
即 .又
故
或 .
若 ,则直线l的方程为 ,
过点 ,与题意矛盾,所以 ,故 ,
所以直线l的方程为 ,过点 .
【点睛】关键点睛:利用一元二次方程根与系数的关系是解题的关键.
第22页/共23页
学科网(北京)股份有限公司第23页/共23页
学科网(北京)股份有限公司