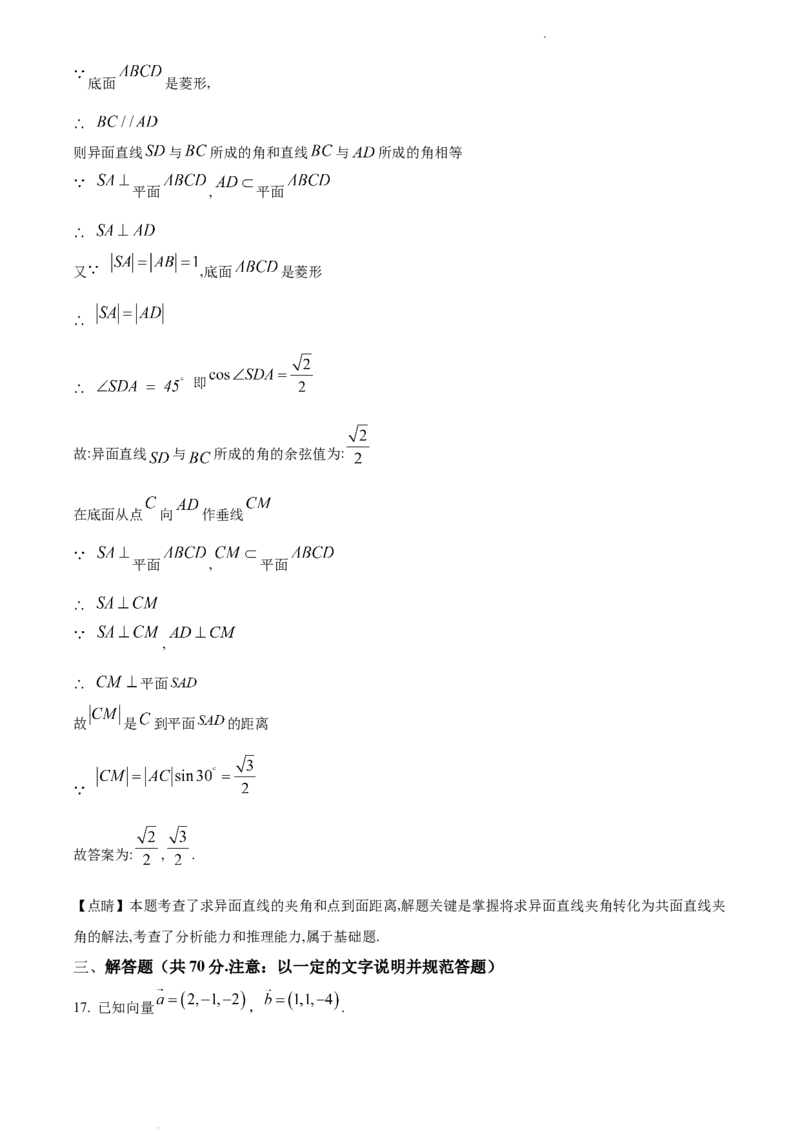文档内容
期末数学试卷
(时间:120分钟 满分:150分)
注意事项:1.答题前在答题卷上填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卷上.
一、选择题(每小题5分,共60分.注意:9至12题为多选题.)
1. 过点 , 的直线的斜率等于1,则m的值为( )
A. 1 B. 4 C. 1或3 D. 1或4
【答案】A
【解析】
【分析】解方程 即得解.
【详解】由题得 .
故选:A
【点睛】本题主要考查斜率的计算,意在考查学生对该知识的理解掌握水平.
2. 若圆 的半径为 ,则实数 ( )
A. B. -1 C. 1 D.
【答案】B
【解析】
【分析】将圆的方程化为标准方程,即可求出半径的表达式,从而可求出 的值.
【详解】由题意,圆的方程可化为 ,
所以半径为 ,解得 .
故选:B.
【点睛】本题考查圆的方程,考查学生的计算求解能力,属于基础题.
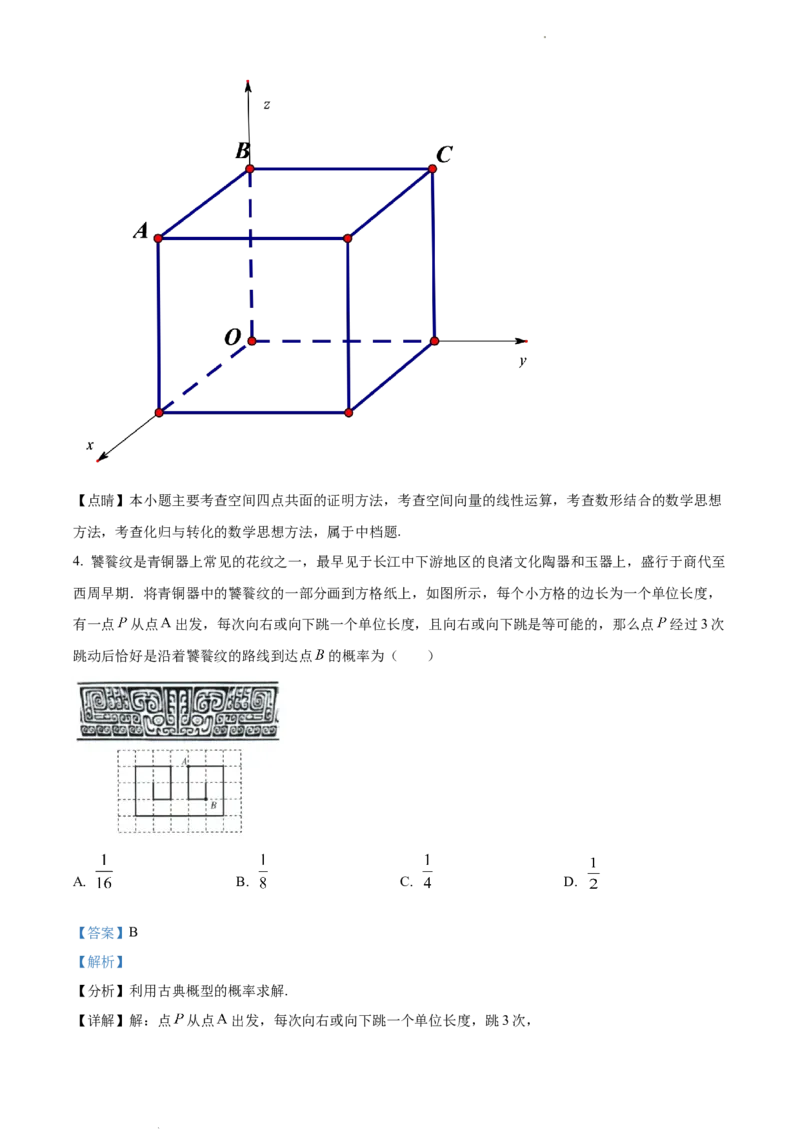
3. 已知A,B,C三点不共线,O是平面ABC外一点,下列条件中能确定点M与点A,B,C一定共面的是
A. B.
学科网(北京)股份有限公司C. D.
【答案】D
【解析】
【分析】首先利用坐标法,排除错误选项,然后对符合的选项验证存在 使得 ,由
此得出正确选项.
【详解】不妨设 .
对于A选项, ,由于 的竖坐标 ,故 不在平面 上,故A
选项错误.
对于B选项, ,由于 的竖坐标 ,故 不在平面 上,故
B选项错误.
对于C选项, ,由于 的竖坐标 ,故 不在平面
上,故C选项错误.
对于D选项, ,由于 的竖坐标为 ,故 在平面 上,也
即 四点共面.下面证明结论一定成立:
由 ,得 ,
即 ,故存在 ,使得 成立,也即 四点共面.
故选:D.
学科网(北京)股份有限公司【点睛】本小题主要考查空间四点共面的证明方法,考查空间向量的线性运算,考查数形结合的数学思想
方法,考查化归与转化的数学思想方法,属于中档题.
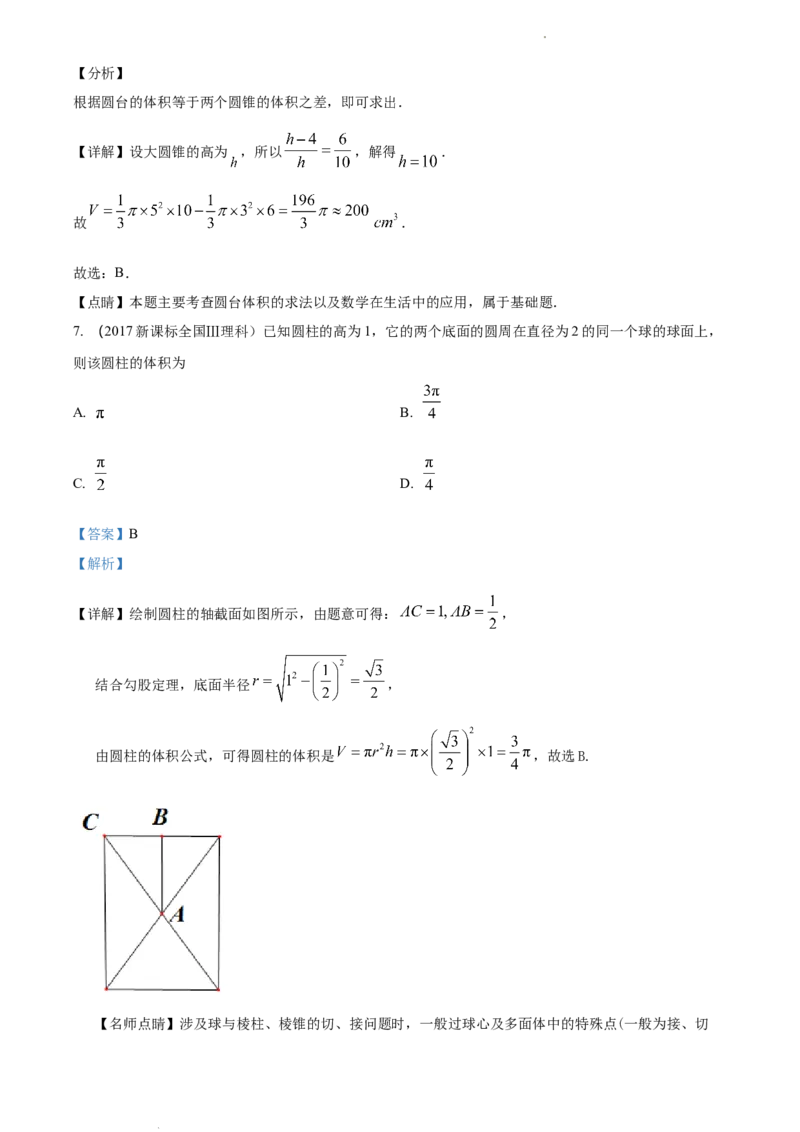
4. 饕餮纹是青铜器上常见的花纹之一,最早见于长江中下游地区的良渚文化陶器和玉器上,盛行于商代至
西周早期.将青铜器中的饕餮纹的一部分画到方格纸上,如图所示,每个小方格的边长为一个单位长度,
有一点 从点 出发,每次向右或向下跳一个单位长度,且向右或向下跳是等可能的,那么点 经过3次
跳动后恰好是沿着饕餮纹的路线到达点 的概率为( )
A. B. C. D.
【答案】B
【解析】
【分析】利用古典概型的概率求解.
【详解】解:点 从点 出发,每次向右或向下跳一个单位长度,跳3次,
学科网(北京)股份有限公司则样本空间 {(右,右,右),(右,右,下),(右,下,右),(下,右,右),(右,下,
下),(下,右,下),(下,下,右),(下,下,下)},
记“3次跳动后,恰好是沿着饕餮纹的路线到达点B”为事件 ,则 {(下,下,右)},由古典概型
的概率公式可知 .
故选:B.
5. 点 到直线 的距离为
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
【分析】直接利用点到直线的距离公式得到答案.
【详解】 ,答案为B
【点睛】本题考查了点到直线的距离公式,属于简单题.
6. 紫砂壶是中国特有的手工制造陶土工艺品,其制作始于明朝正德年间.紫砂壶的壶型众 多,经典的有西施
壶、掇球壶、石瓢壶、潘壶等.其中,石瓢壶的壶体可以近似看成一 个圆台 (即圆锥用平行于底面的平面截
去一个锥体得到的).下图给出了一个石瓢壶的相关数据(单位:cm),那么该壶的容量约为( )
A. 100 B.
C. 300 D. 400
【答案】B
【解析】
学科网(北京)股份有限公司【分析】
根据圆台的体积等于两个圆锥的体积之差,即可求出.
【详解】设大圆锥的高为 ,所以 ,解得 .
故 .
故选:B.
【点睛】本题主要考查圆台体积的求法以及数学在生活中的应用,属于基础题.
7. (2017新课标全国Ⅲ理科)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,
则该圆柱的体积为
A. B.
C. D.
【答案】B
【解析】
【详解】绘制圆柱的轴截面如图所示,由题意可得: ,
结合勾股定理,底面半径 ,
由圆柱的体积公式,可得圆柱的体积是 ,故选B.
【名师点睛】涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切
学科网(北京)股份有限公司点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只
画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,
列方程(组)求解.
8. 已知圆 ,圆 ,M,N分别是圆 上的动点,P
为x轴上的动点,则以 的最小值为( )
.
A B. C. D.
【答案】A
【解析】
【分析】求出圆 关于 轴的对称圆的圆心坐标 ,以及半径,然后求解圆 与圆 的圆心距减去两个
圆的半径和,即可求出 的最小值.
【详解】圆 关于 轴 的对称圆的圆心坐标 ,半径为1,圆 的圆心坐标为 ,半径为3,
易知,当 三点共线时, 取得最小值,
的最小值为圆 与圆 的圆心距减去两个圆的半径和,
即: .
故选:A.
注意: 9至12题为多选题.
9. 已知直线 : 和直线 : ,下列说法正确的是( )
A. 始终过定点
B. 若 ,则 或-3
C. 若 ,则 或2
D. 当 时, 始终不过第三象限
学科网(北京)股份有限公司【答案】ACD
【解析】
【分析】将直线化为 可判断A;将 或-3代入直线方程可判断B;根据
可判断C;将直线化为 ,即可求解.
【详解】 : 过点 ,A正确;
当 时, , 重合,故B错误;
由 ,得 或2,故C正确;
: 始终过 ,斜率为负,不会过第三象限,故D正确.
故选:ACD
【点睛】本题考查了直线过定点、直线垂直求参数,考查了基本运算求解能力,属于基础题.
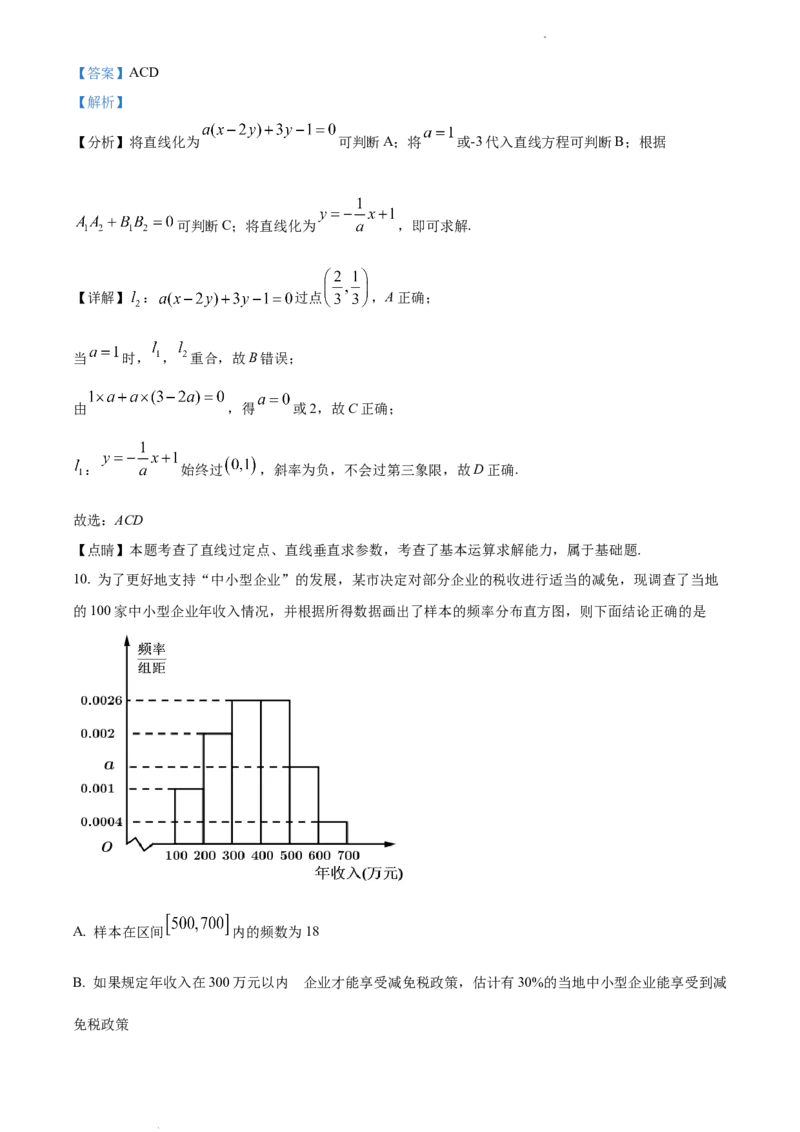
10. 为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,现调查了当地
的100家中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,则下面结论正确的是
A. 样本在区间 内的频数为18
的
B. 如果规定年收入在300万元以内 企业才能享受减免税政策,估计有30%的当地中小型企业能享受到减
免税政策
学科网(北京)股份有限公司C. 样本的中位数小于350万元
D. 可估计当地的中小型企业年收入的平均数超过400万元(同一组中的数据用该组区间的中点值为代表
【答案】AB
【解析】
【分析】
由题意和图形及频率分布直方图的相关公式计算频率、中位数、平均数即可,
【详解】由图可得
样本在区间 内的频数为 ,故A正确;
年收入在300万元以内的企业频率为 ,故B正确;
则中位数在 之间,设为 则
,故C不正确;
年收入的平均数超过 ,
故D不正确
故选:AB
【点睛】方法点睛:1.谨记频率分布直方图的相关公式:
(1)直方图中各小长方形的面积之和为1;
(2)直方图中纵轴表示:频率/组距,故每组样本的频率为组距乘以频率/组距,即矩形的面积;
(3)直方图中每组样本的频数为频率乘以总数.
2.频率分布直方图中数字特征的计算:
(1)最高的小长方形底边中点的横坐标即是众数;
(2)中位数左边和右边的小长方形的面积和是相等的;
(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中
点的横坐标之和.
11. 设 , 是两个平面, , 是两条直线,下列命题正确的是( )
A. 如果 , ,那么 .
B. 如果 , ,那么 .
学科网(北京)股份有限公司C. 如果 , , ,那么 .
D. 如果 内有两条相交直线与 平行,那么 .
【答案】ABD
【解析】
【分析】由立体几何知识对选项逐一判断
【详解】对于A,由线面垂直的性质知A正确
对于B,由面面平行的性质知B正确
对于C,若 , , ,可得 或 ,而 位置关系不确定,故C错误
对于D,由面面平行的判定定理知D正确
故选:ABD
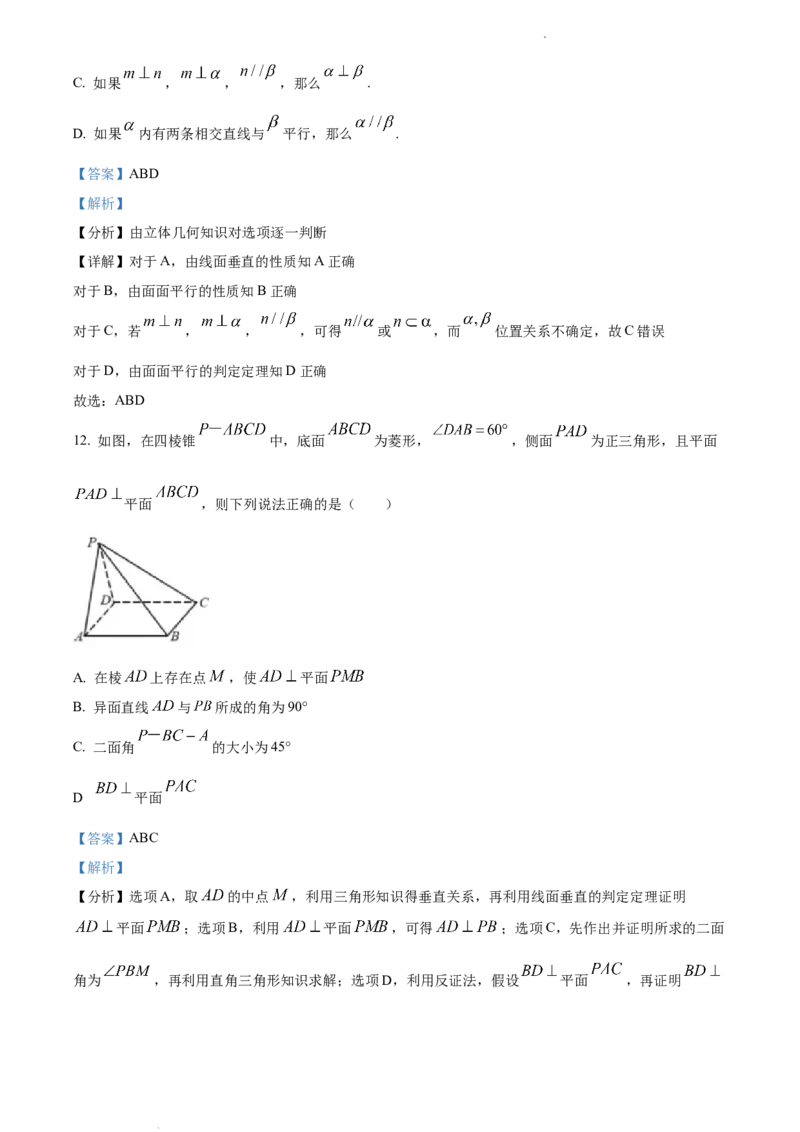
12. 如图,在四棱锥 中,底面 为菱形, ,侧面 为正三角形,且平面
平面 ,则下列说法正确的是( )
A. 在棱 上存在点 ,使 平面
B. 异面直线 与 所成的角为90°
C. 二面角 的大小为45°
.
D 平面
【答案】ABC
【解析】
【分析】选项A,取 的中点 ,利用三角形知识得垂直关系,再利用线面垂直的判定定理证明
平面 ;选项B,利用 平面 ,可得 ;选项C,先作出并证明所求的二面
角为 ,再利用直角三角形知识求解;选项D,利用反证法,假设 平面 ,再证明
学科网(北京)股份有限公司平面 ,得到 ,与 与 的夹角为 矛盾来说明.
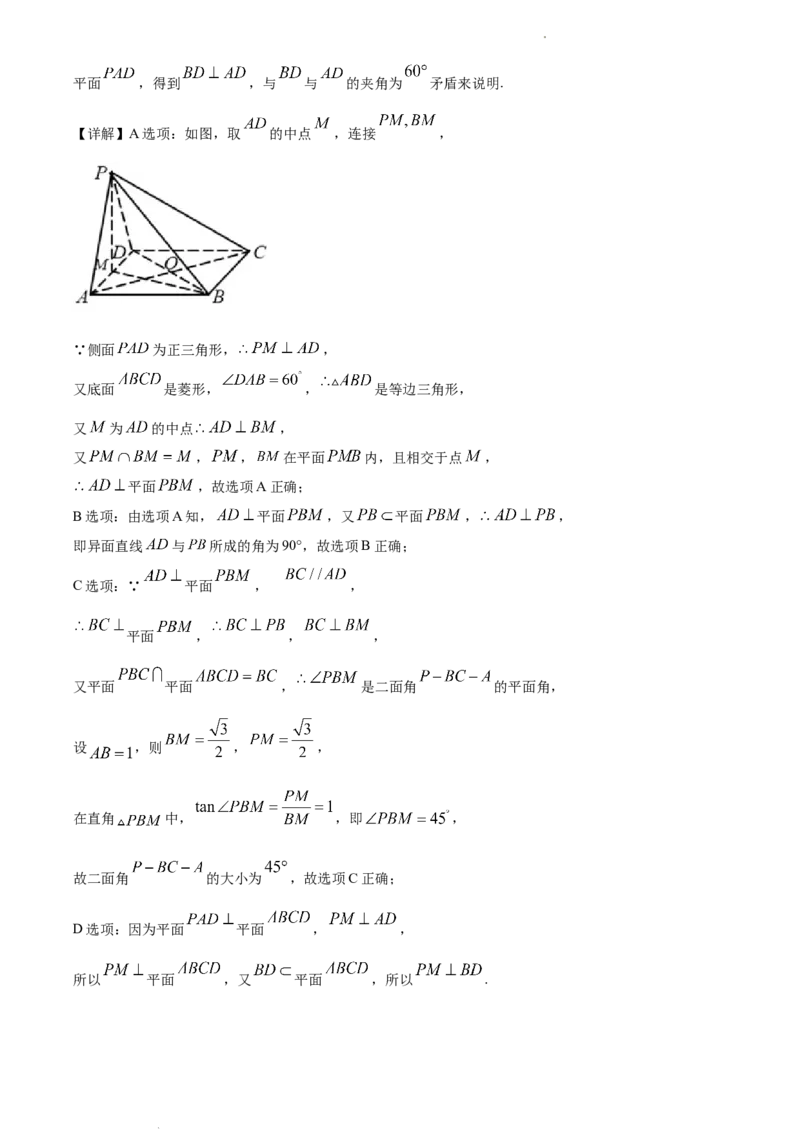
【详解】A选项:如图,取 的中点 ,连接 ,
∵侧面 为正三角形, ,
又底面 是菱形, , 是等边三角形,
又 为 的中点 ,
又 , , 在平面 内,且相交于点 ,
平面 ,故选项A正确;
B选项:由选项A知, 平面 ,又 平面 , ,
即异面直线 与 所成的角为90°,故选项B正确;
C选项:∵ 平面 , ,
平面 , , ,
又平面 平面 , 是二面角 的平面角,
设 ,则 , ,
在直角 中, ,即 ,
故二面角 的大小为 ,故选项C正确;
D选项:因为平面 平面 , ,
所以 平面 ,又 平面 ,所以 .
学科网(北京)股份有限公司假设 平面 ,则有 ,又 , 在平面 内,且相交于点 ,
所以 平面 ,又 平面 ,所以 ,
而由题可知, 与 的夹角为 ,矛盾,故假设不成立,故选项D错误.
故选:ABC.
二、填空题(每小题5分,共20分)
13. 已知圆锥的高为 ,体积为 ,则以该圆锥的母线为半径的球的表面积为______________.
【答案】
【解析】
【分析】利用圆锥体积公式可求得圆锥底面半径 ,利用勾股定理可得母线长 ;根据球的表面积公式可
求得结果.
【详解】设圆锥的底面半径为 ,母线长为 ,
圆锥体积 , , ,
以 为半径的球的表面积 .
故答案为: .
14. 直线 的倾斜角的取值范围是______.
【答案】
【解析】
【分析】先求出直线的斜率取值范围,再根据斜率与倾斜角的关系,即可求出.
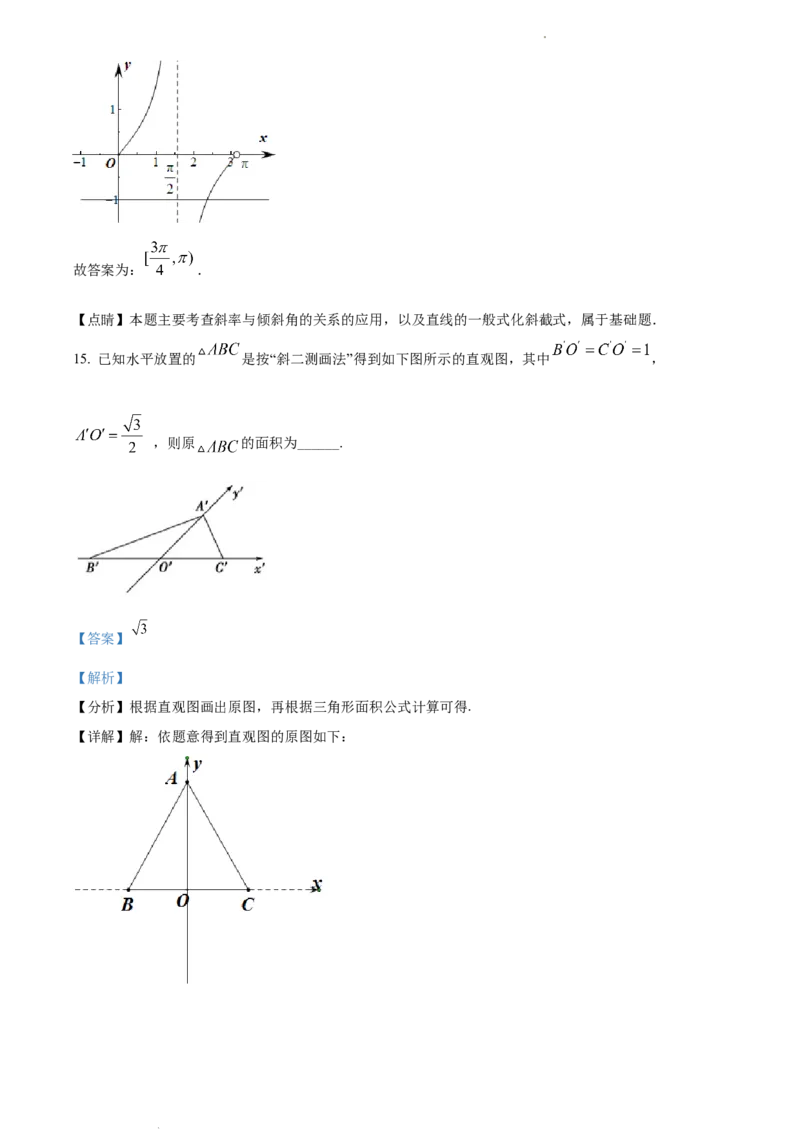
【详解】 可化为: ,所以 ,由于
,结合函数 在 上的图象,可知 .
学科网(北京)股份有限公司故答案为: .
【点睛】本题主要考查斜率与倾斜角的关系的应用,以及直线的一般式化斜截式,属于基础题.
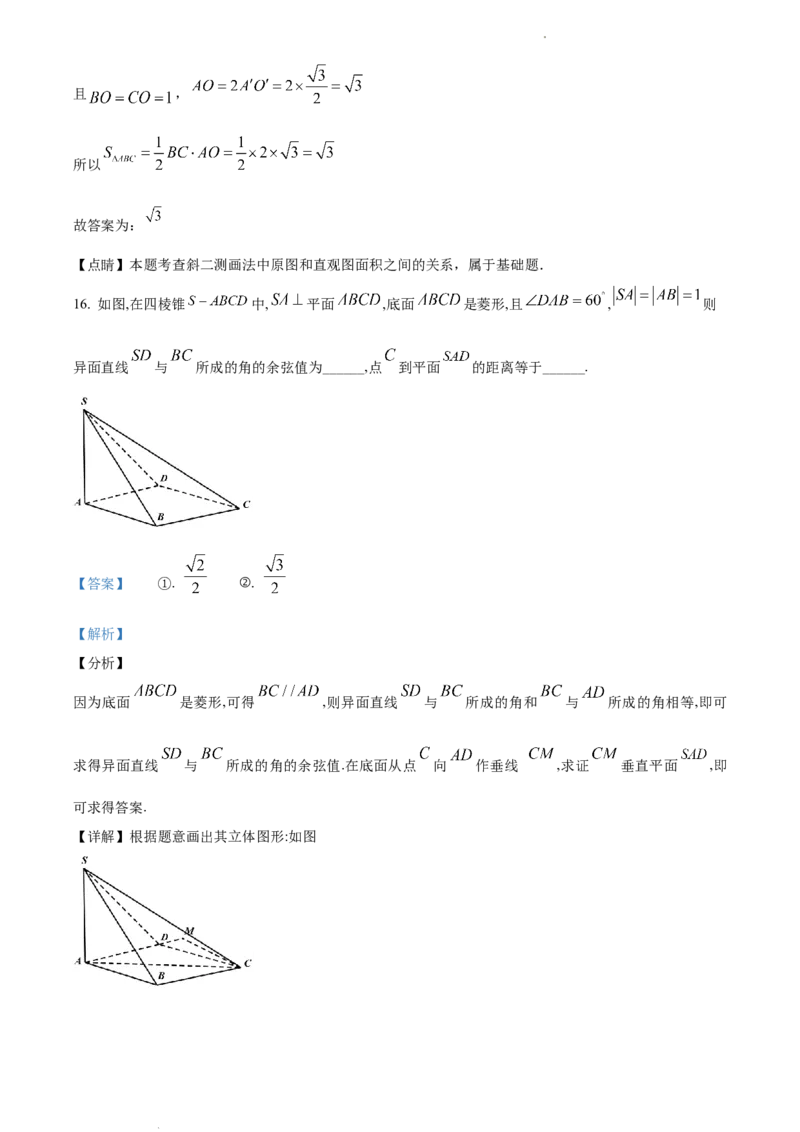
15. 已知水平放置的 是按“斜二测画法”得到如下图所示的直观图,其中 ,
,则原 的面积为______.
【答案】
【解析】
【分析】根据直观图画出原图,再根据三角形面积公式计算可得.
【详解】解:依题意得到直观图的原图如下:
学科网(北京)股份有限公司且 ,
所以
故答案为:
【点睛】本题考查斜二测画法中原图和直观图面积之间的关系,属于基础题.
16. 如图,在四棱锥 中, 平面 ,底面 是菱形,且 , 则
异面直线 与 所成的角的余弦值为______,点 到平面 的距离等于______.
【答案】 ①. ②.
【解析】
【分析】
因为底面 是菱形,可得 ,则异面直线 与 所成的角和 与 所成的角相等,即可
求得异面直线 与 所成的角的余弦值.在底面从点 向 作垂线 ,求证 垂直平面 ,即
可求得答案.
【详解】根据题意画出其立体图形:如图
学科网(北京)股份有限公司底面 是菱形,
则异面直线 与 所成的角和直线 与 所成的角相等
平面 , 平面
又 ,底面 是菱形
即
故:异面直线 与 所成的角的余弦值为:
在底面从点 向 作垂线
平面 , 平面
,
平面
故 是 到平面 的距离
故答案为: , .
【点睛】本题考查了求异面直线的夹角和点到面距离,解题关键是掌握将求异面直线夹角转化为共面直线夹
角的解法,考查了分析能力和推理能力,属于基础题.
三、解答题(共70分.注意:以一定的文字说明并规范答题)
17. 已知向量 , .
学科网(北京)股份有限公司(1)计算 和 ;
(2)求 .
【答案】(1) , ;(2) .
【解析】
【分析】
(1)利用空间向量的坐标运算可求得 的坐标,利用向量的模长公式可求得 的值;
(2)计算出 ,结合 的取值范围可求得结果.
【详解】(1) , ;
(2) ,
,因此, .
【点睛】本题考查空间向量的坐标运算,同时也考查了利用空间向量的数量积计算向量的夹角,考查计算
能力,属于基础题.
18. 已知三角形的三个顶点是 , , .
(1)求 边上的中线所在直线的方程;
(2)求 边上的高所在直线的方程.
【答案】(1) ;(2) .
【解析】
【分析】(1)先求出BC的中点坐标,再利用两点式求出直线的方程;
(2)先求出BC边上的高所在直线的斜率,再利用点斜式求出直线的方程.
【详解】(1)设线段 的中点为 .
因为 , ,
学科网(北京)股份有限公司所以 的中点 ,
所以 边上的中线所在直线的方程为 ,
即 .
(2)因为 , ,
所以 边所在直线的斜率 ,
所以 边上的高所在直线的斜率为 ,
所以 边上的高所在直线的方程为 ,
即 .
【点睛】本题主要考查直线方程的求法,属于基础题.
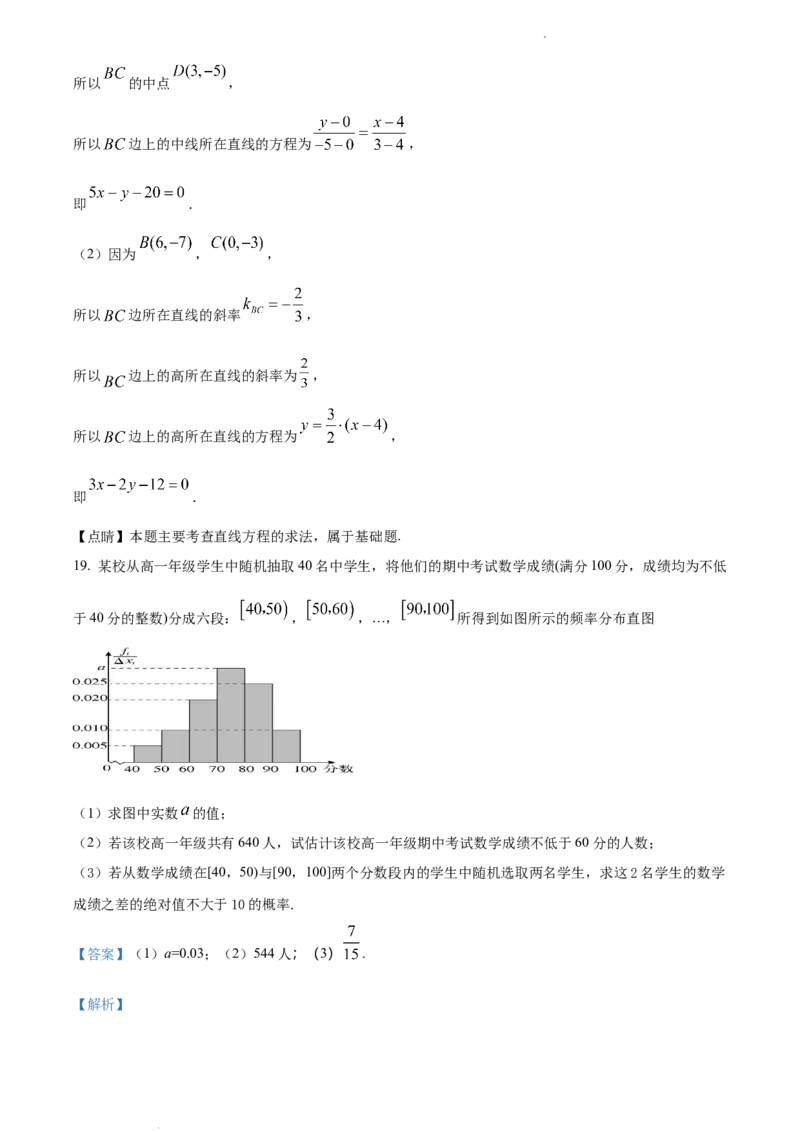
19. 某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低
于40分的整数)分成六段: , ,…, 所得到如图所示的频率分布直图
(1)求图中实数 的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这2名学生的数学
成绩之差的绝对值不大于10的概率.
【答案】(1)a=0.03;(2)544人;(3) .
【解析】
学科网(北京)股份有限公司【分析】(1)根据图中所有小矩形的面积之和等于1求解.
(2)根据频率分布直方图,得到成绩不低于60分的频率,再根据该校高一年级共有学生640人求解.
(3)由频率分布直方图得到成绩在[40,50)和[90,100]分数段内的人数,先列举出从数学成绩在[40,50)
与[90,100]两个分数段内的学生中随机选取两名学生的基本事件总数,再得到两名学生的数学成绩之差的
绝对值不大于10”的基本事件数,代入古典概型概率求解.
【详解】(1)∵图中所有小矩形的面积之和等于1,
∴10×(0.005+0.01+0.02+a+0.025+0.01)=1,
解得a=0.03.
(2)根据频率分布直方图,成绩不低于60分的频率为1−10×(0.005+0.01)=0.85,
∵该校高一年级共有学生640人,
∴由样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为640×0.85=544人.
(3)成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B,
成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.
若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,
则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),
(C,D),(C,E),
(C,F),(D,E),(D,F),(E,F)共15种.
如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,
的
那么这两名学生 数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.
∴所求概率为P(M)= .
【点睛】本题主要考查频率分布直方图的应用以及古典概型概率的求法,还考查了运算求解的能力,属于
中档题.
20. 如图长方体 中, , ,点 为 的中点.
学科网(北京)股份有限公司(1)求证: 平面 ;
(2)求证: 平面 ;
(3)求二面角 的余弦值.
【答案】(1)见解析(2)见解析(3)
【解析】
【分析】(1)作辅助线,由中位线定理证明 ,再由线面平行的判定定理证明即可;
(2)连接 ,由勾股定理证明 , ,再结合线面垂直的判定定理证明即可;
(3)建立空间直角坐标系,利用向量法求面面角的余弦值即可.
【详解】(1)连接 交 与点 ,连接
四边形 为正方形, 点 为 的中点
又点 为 的中点,
平面 , 平面
平面
学科网(北京)股份有限公司(2)连接
由勾股定理可知 ,
,则
同理可证 ,
平面
平面
(3)建立如下图所示的空间直角坐标系
显然平面 的法向量即为平面 的法向量,不妨设为
学科网(北京)股份有限公司由(2)可知 平面 ,即平面 的法向量为
又二面角 是钝角
二面角 的余弦值为
【点睛】关键点睛:在第一问中,关键是利用中位线定理找到线线平行,再由定义证明线面平行;在第二
问中,关键是利用勾股定理证明线线垂直,从而得出线面垂直;在第三问中,关键是建立坐标系,利用向
量法求面面角的余弦值.
21. 已知圆 .
(1)求过点M(2,1)的圆的切线方程;
(2)直线 过点 且被圆 截得的弦长为2,求直线 的方程;
(3)已知圆 的圆心在直线y=1上,与y轴相切,且与圆 相外切,求圆 的标准方程.
【答案】(1)y=1;
(2)x+y-2=0;
(3) .
【解析】
【分析】(1)将圆的一般方程化为圆的标准方程,结合图形即可求出结果;
学科网(北京)股份有限公司(2)根据题意可知直线 过圆心 ,利用直线的两点式方程计算即可得出结果;
(3)设圆E的圆心E(a,1),根据题意可得圆E的半径为 ,结合圆与圆的位置关系和两点距离公式计算
求出 ,进而得出圆的标准方程.
【小问1详解】
圆 ,
即 ,
其圆心为 ,半径为1.
因为点(2,1)在圆上,如图,
所以切线方程为y=1;
【小问2详解】
由题意得,圆的直径为2,
所以直线 过圆心 ,
由直线的两点式方程,得 ,
即直线 的方程为x+y-2=0;
【小问3详解】
因为圆E的圆心在直线y=1上,设圆E的圆心E(a,1),
由圆E与y轴相切,得R=a( )
又圆E与圆 相外切,所以 ,
由两点距离公式得 ,
学科网(北京)股份有限公司所以 ,解得 ,
所以圆心 , ,
所以圆E的方程为 .
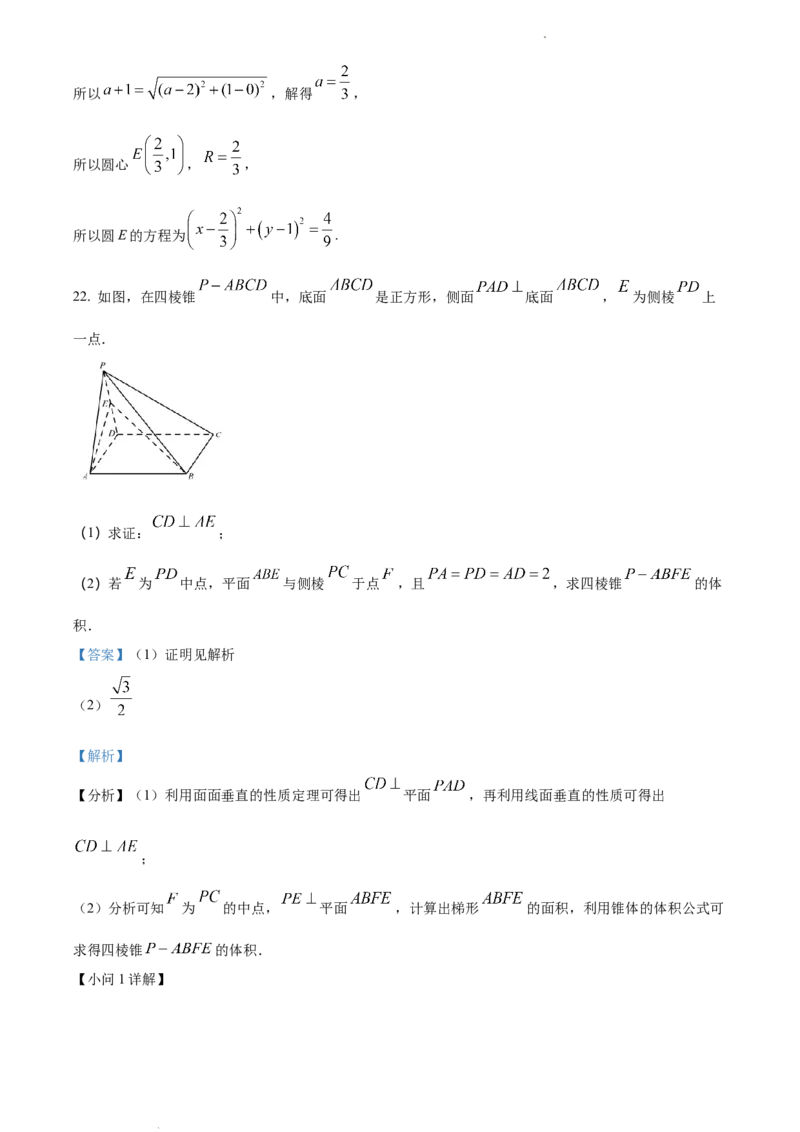
22. 如图,在四棱锥 中,底面 是正方形,侧面 底面 , 为侧棱 上
一点.
(1)求证: ;
(2)若 为 中点,平面 与侧棱 于点 ,且 ,求四棱锥 的体
积.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)利用面面垂直的性质定理可得出 平面 ,再利用线面垂直的性质可得出
;
(2)分析可知 为 的中点, 平面 ,计算出梯形 的面积,利用锥体的体积公式可
求得四棱锥 的体积.
【小问1详解】
学科网(北京)股份有限公司证明:因为四边形 为正方形,则 ,
因为侧面 底面 ,平面 平面 , 平面 ,
所以 平面 ,又 平面 ,所以 .
【小问2详解】
解:因为 , 平面 , 平面 ,所以, 平面 ,
因为 平面 ,平面 平面 ,所以 ,所以 ,
,则 ,所以,四边形 是直角梯形,
又 是 中点,所以 , ,
所以 ,
由 平面 , 平面 ,所以 ,从而 ,
正三角形 中, 是 中点, ,即 ,
,所以 平面 ,
因为 ,所以 .
学科网(北京)股份有限公司学科网(北京)股份有限公司