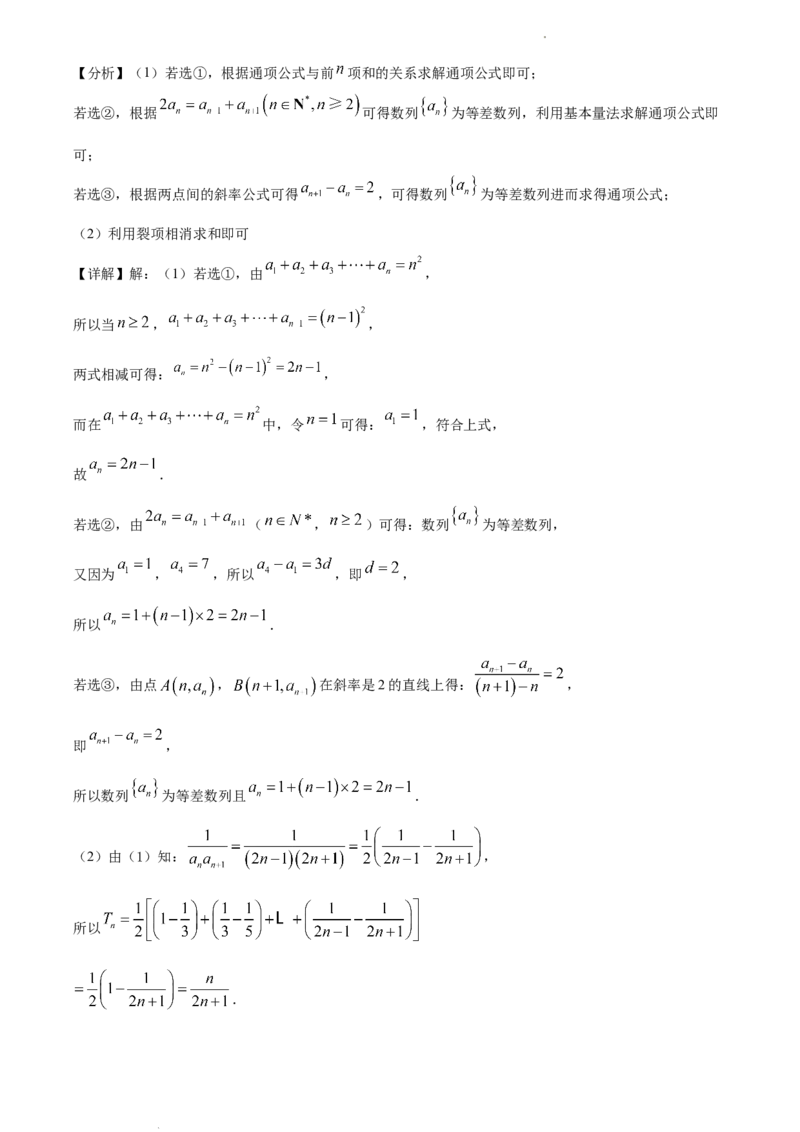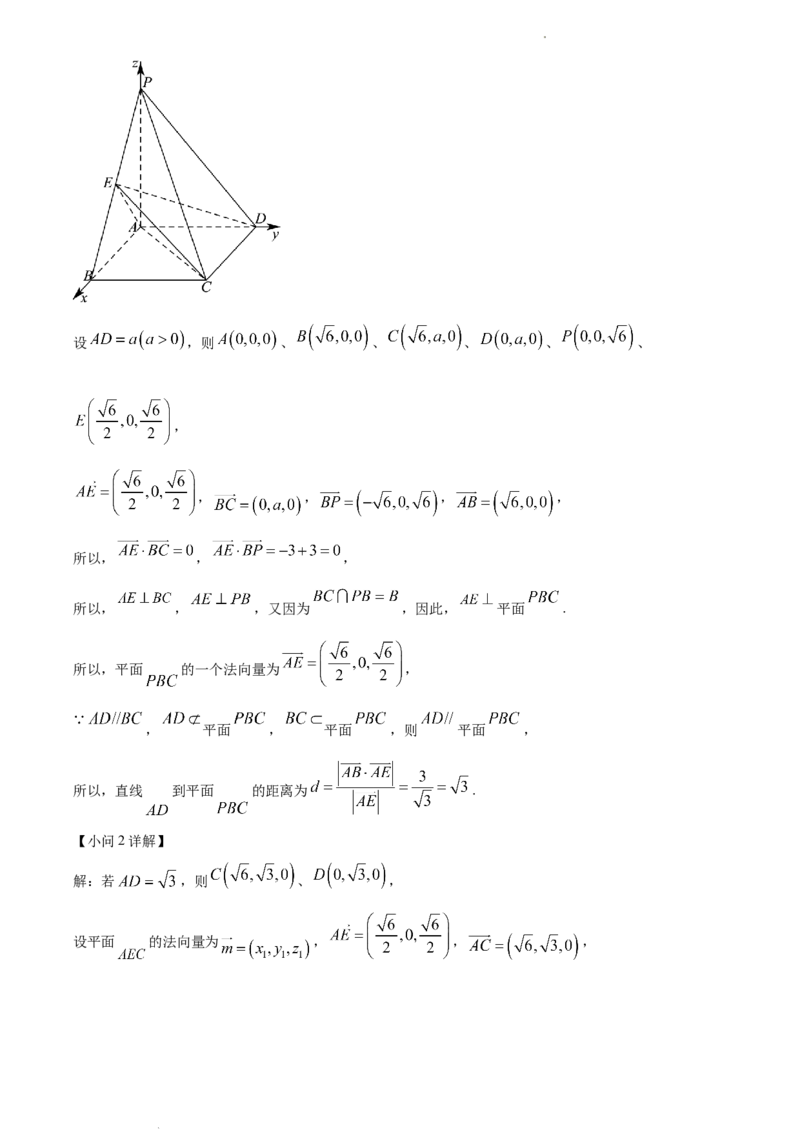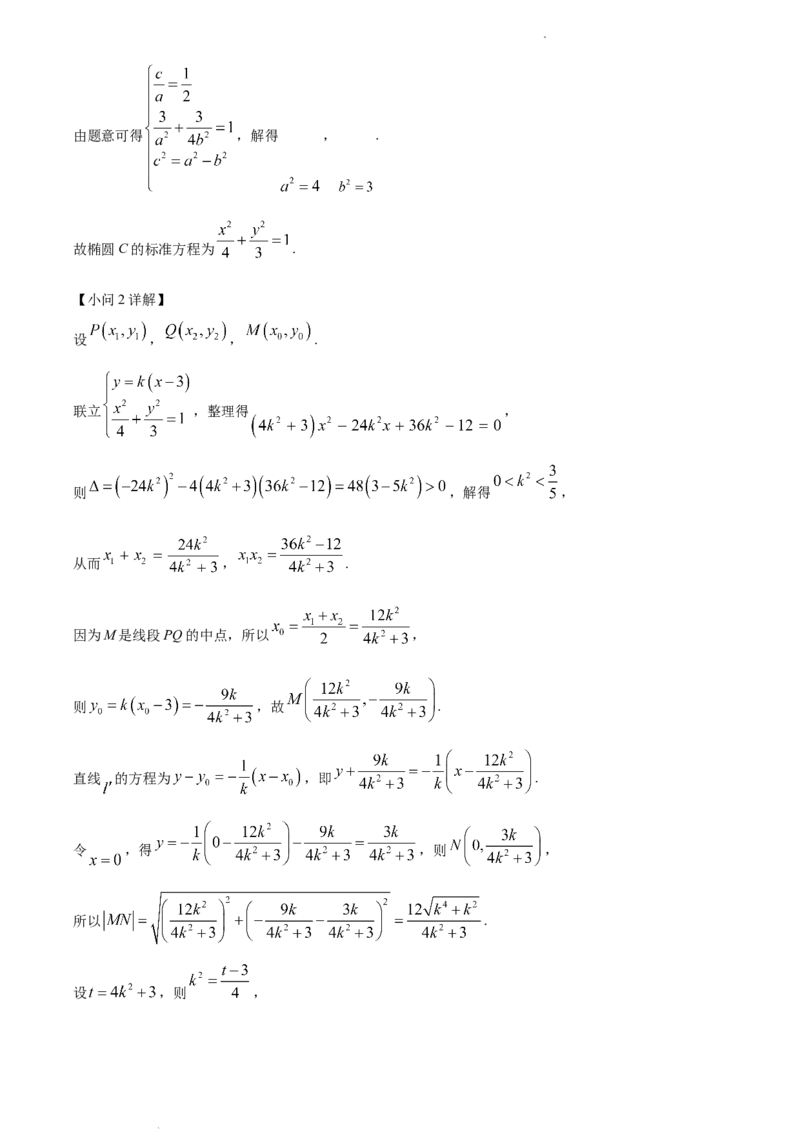文档内容
第一学期期末教学质量监测
高二数学试卷
一、单选题:本大题共8小题,每小题5分,共40分.
.
1 已知集合A= ( )
A. B.
C. 或 D.
【答案】A
【解析】
【分析】先求出集合 ,再根据集合的交集运算,即可求出结果.
【详解】因为集合 ,
所以 .
故选:A.
2. 已知 是虚数单位,若复数 满足 ,则 ( ).
A. B. 2 C. D. 4
【答案】C
【解析】
【分析】先求出 ,然后根据复数的模求解即可
【详解】 ,
,
则 ,
学科网(北京)股份有限公司故选:C
3. 若 构成空间的一个基底,则下列向量能构成空间的一个基底的是( )
A. , , B. , ,
C. , , D. , ,
【答案】B
【解析】
【分析】由空间向量内容知,构成基底的三个向量不共面,对选项逐一分析
【详解】对于A: ,因此A不满足题意;
对于B:根据题意知道 , , 不共面,而 和 显然位于向量 和向量 所成平面内,与向量
不共面,因此B正确;
对于C: ,故C不满足题意;
对于D:显然有 ,选项D不满足题意.
故选:B
4. 等比数列{ }中,已知 =8, + =4,则 的值为( )
A. 1 B. 2 C. 3 D. 5
【答案】C
【解析】
【分析】由等比数列性质求出公比,将原式化简后计算
【详解】设等比数列{ }的公比为 ,则 = , = ,所以 = = .
又 + = + =( + ) =8× =2,
+ = + =( + ) =8× =1,
学科网(北京)股份有限公司所以 + + + =2+1=3.
故选:C
的
5. △ABC 两个顶点坐标A(-4,0),B(4,0),它的周长是18,则顶点C的轨迹方程是( )
A. B. (y≠0)
C. D.
【答案】D
【解析】
【分析】根据三角形的周长得出 ,再由椭圆的定义得顶点C的轨迹为以A,B为焦
点的椭圆,去掉A,B,C共线的情况,可求得顶点C的轨迹方程.
【详解】因为 ,所以 ,
所以顶点C的轨迹为以A,B为焦点的椭圆,去掉A,B,C共线的情况,即 ,
所以顶点C的轨迹方程是 ,
故选:D.
【点睛】本题考查椭圆的定义,由定义求得动点的轨迹方程,求解时,注意去掉不满足的点,属于基础题.
的
6. 算盘是中国传统 计算工具,是中国人在长期使用算筹的基础上发明的,“珠算”一词最早见于东汉徐岳
所撰的《数术记遗》,其中有云:“珠算控带四时,经纬三才.”北周甄鸾为此作注,大意是:把木板刻为
3部分,上、下两部分是停游珠用的,中间一部分是作定位用的.下图是一把算盘的初始状态,自右向左,
分别是个位、十位、百位…,上面一粒珠(简称上珠)代表5,下面一粒珠(简称下珠)是1,即五粒下珠
的大小等于同组一粒上珠的大小.现在从个位和十位这两组中随机选择往下拨一粒上珠,往上拨3粒下珠,
得到的数为质数(除了1和本身没有其它的约数)的概率是( )
学科网(北京)股份有限公司A. B. C. D.
【答案】B
【解析】
【分析】根据古典概型概率计算公式,计算出所求的概率.
【详解】依题有,算盘所表示的数可能有:17,26,8,35,62,71,80,53,其中是质数的有:17,
71,53,故所求事件的概率为 .
故选:B
7. 直线 分别与 轴, 轴交于 , 两点,点 在圆 上,则 面积
的取值范围是
A. B. C. D.
【答案】A
【解析】
【详解】分析:先求出A,B两点坐标得到 再计算圆心到直线距离,得到点P到直线距离范围,由面
积公式计算即可
详解: 直线 分别与 轴, 轴交于 , 两点
,则
点P在圆 上
圆心为(2,0),则圆心到直线距离
学科网(北京)股份有限公司故点P到直线 的距离 的范围为
则
故答案选A.
点睛:本题主要考查直线与圆,考查了点到直线的距离公式,三角形的面积公式,属于中档题.
8. 已知 , 是球 的球面上两点, , 为该球面上的动点,若三棱锥 体积的
最大值为36,则球 的表面积为( )
A. B. C. D.
【答案】C
【解析】
【分析】当 平面 时,三棱锥 体积最大,根据棱长与球半径关系即可求出球半径,
从而求出表面积.
【详解】当 平面 时,三棱锥 体积最大.
又 ,则三棱锥体积 ,解得 ;
故表面积 .
故选:C.
【点睛】关键点点睛:本题考查三棱锥与球的组合体的综合问题,本题的关键是判断当 平面
时,三棱锥 体积最大.
二、多选题:本大题共4小题,共20分.在每小题给出的选项中,有多个符合题目要求.全部选
对的得5分,有选错的得0分,部分选对的得2分.
9. 已知数列 满足 , ,则下列各数是 的项的有( )
学科网(北京)股份有限公司A. B. C. D.
【答案】BD
【解析】
【分析】根据递推关系式找出规律,可得数列是周期为3的周期数列,从而可求解结论.
【详解】因为数列 满足 , ,
;
;
;
数列 是周期为3的数列,且前3项为 , ,3;
故选: .
【点睛】本题主要考查数列递推关系式的应用,考查数列的周期性,解题的关键在于求出数列的规律,属
于基础题.
10. 血压(bloodpressure,BP)是指血液在血管内流动时作用于单位面积血管壁的侧压力,它是推动血液
在血管内流动的动力,血压的最大值、最小值分别称为收缩压和舒张压.未使用抗高血压药的前提下,18岁
以上成人收缩压 或舒张压 ,则说明这位成人有高血压,设从未使用抗高血压药
的李华今年40岁,从某天早晨6点开始计算(即早晨6点时, ),他的血压 ( )与经
过的时间 ( )满足关系式 ,则( )
A. 函数 的最小正周期为6 B. 当天早晨7点时李华的血压为
学科网(北京)股份有限公司C. 当天李华有高血压 D. 当天李华的收缩压与舒张压之差为
【答案】BCD
【解析】
【分析】由正弦型函数的特征分别对四个选项所求内容进行分析计算即可得解.
【详解】因为 ,所以 ;
当 时, ,所以当天早晨7点时李华的血压为 ;
因为 的最大值为 ,最小值为 ,所以李华的收缩压为 ,
舒张压为 ,因此李华有高血压,且他的收缩压与舒张压之差为 .
故选:BCD.
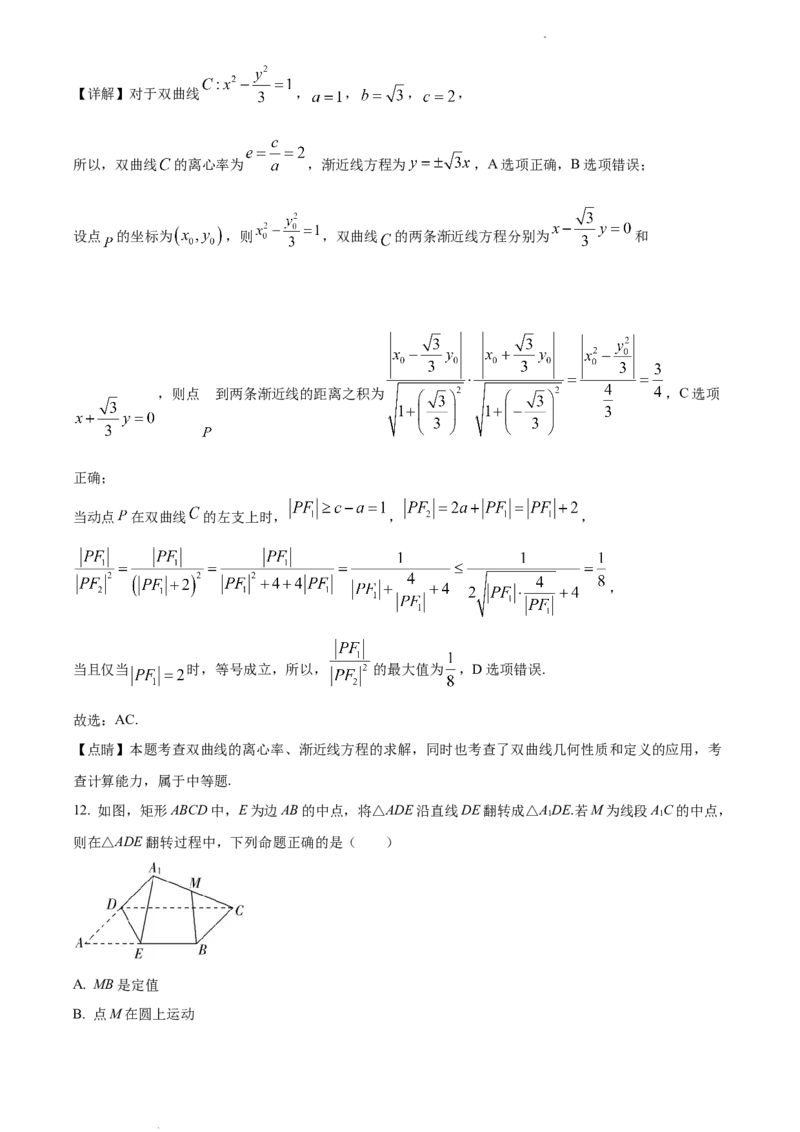
11. 已知动点 在双曲线 上,双曲线 的左、右焦点分别为 、 ,下列结论正确的是(
)
A. 的离心率为
B. 的渐近线方程为
C. 动点 到两条渐近线的距离之积为定值
D. 当动点 在双曲线 的左支上时, 的最大值为
【答案】AC
【解析】
【分析】根据双曲线 的方程求出 、 、 的值,可求得双曲线 的离心率和渐近线方程,可判断A、
B选项的正误;设点 的坐标为 ,利用点到直线的距离公式结合双曲线 的方程可判断C选项的
正误;利用双曲线的定义和基本不等式可判断D选项的正误.
学科网(北京)股份有限公司【详解】对于双曲线 , , , ,
所以,双曲线 的离心率为 ,渐近线方程为 ,A选项正确,B选项错误;
设点 的坐标为 ,则 ,双曲线 的两条渐近线方程分别为 和
,则点 到两条渐近线的距离之积为 ,C选项
正确;
当动点 在双曲线 的左支上时, , ,
,
当且仅当 时,等号成立,所以, 的最大值为 ,D选项错误.
故选:AC.
【点睛】本题考查双曲线的离心率、渐近线方程的求解,同时也考查了双曲线几何性质和定义的应用,考
查计算能力,属于中等题.
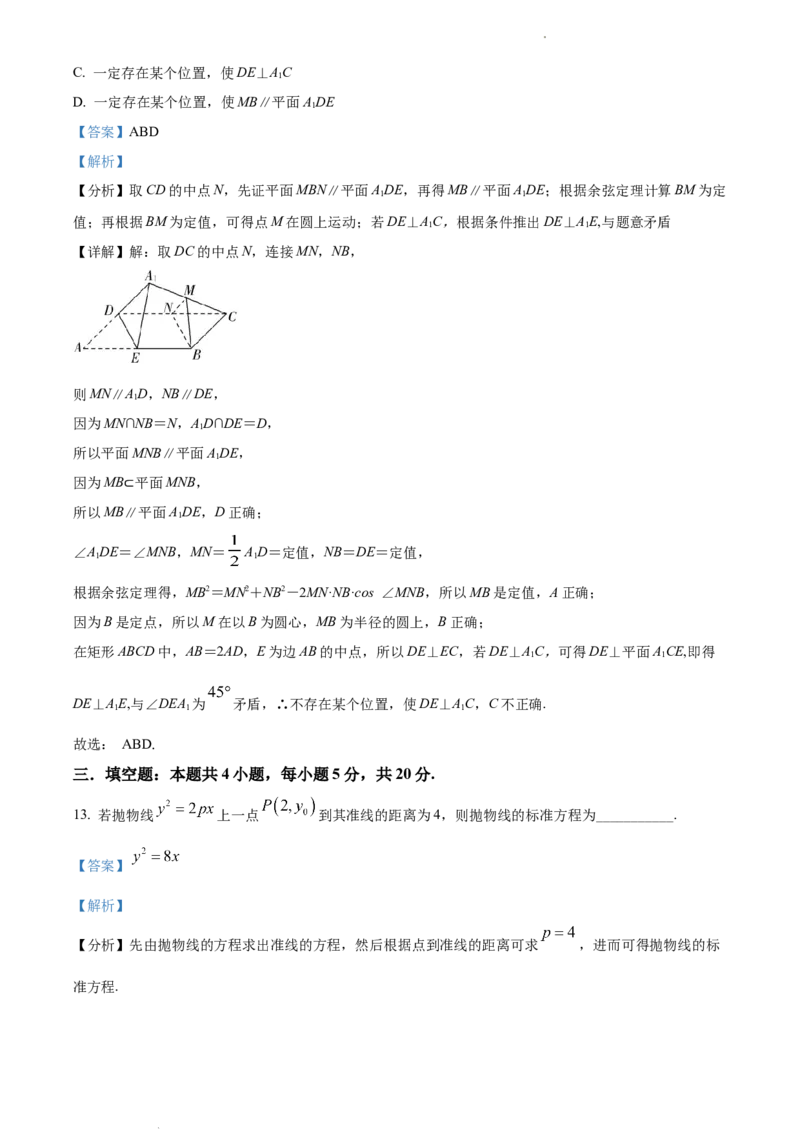
12. 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△ADE.若M为线段AC的中点,
1 1
则在△ADE翻转过程中,下列命题正确的是( )
A. MB是定值
B. 点M在圆上运动
学科网(北京)股份有限公司C. 一定存在某个位置,使DE⊥AC
1
D. 一定存在某个位置,使MB∥平面ADE
1
【答案】ABD
【解析】
【分析】取CD的中点N,先证平面MBN∥平面ADE,再得MB∥平面ADE;根据余弦定理计算BM为定
1 1
值;再根据BM为定值,可得点M在圆上运动;若DE⊥AC,根据条件推出DE⊥AE,与题意矛盾
1 1
【详解】解:取DC的中点N,连接MN,NB,
则MN∥AD,NB∥DE,
1
因为MN∩NB=N,AD∩DE=D,
1
所以平面MNB∥平面ADE,
1
因为MB 平面MNB,
所以MB⊂∥平面A
1
DE,D正确;
∠ADE=∠MNB,MN= AD=定值,NB=DE=定值,
1 1
根据余弦定理得,MB2=MN2+NB2-2MN·NB·cos ∠MNB,所以MB是定值,A正确;
因为B是定点,所以M在以B为圆心,MB为半径的圆上,B正确;
在矩形ABCD中,AB=2AD,E为边AB的中点,所以DE⊥EC,若DE⊥AC,可得DE⊥平面ACE,即得
1 1
DE⊥AE,与∠DEA 为 矛盾,∴不存在某个位置,使DE⊥AC,C不正确.
1 1 1
故选: ABD.
三.填空题:本题共4小题,每小题5分,共20分.
13. 若抛物线 上一点 到其准线的距离为4,则抛物线的标准方程为___________.
【答案】
【解析】
【分析】先由抛物线的方程求出准线的方程,然后根据点到准线的距离可求 ,进而可得抛物线的标
准方程.
学科网(北京)股份有限公司【详解】抛物线的准线方程为 ,点 到其准线的距离为 ,
由题意可得 ,解得 ,故抛物线的标准方程为 .
故答案为: .
14. 已知圆锥的母线长为 cm,其侧面展开图是一个半圆,则底面圆的半径为____cm.
【答案】
【解析】
【分析】根据题意可知圆锥侧面展开图的半圆的半径为 cm,再根据底面圆的周长等于侧面的弧长,即
可求出结果.
【详解】设底面圆的半径为 ,
由于侧面展开图是一个半圆,又圆锥的母线长为 cm,
所以该半圆的半径为 cm,
所以 ,所以 (cm).
故答案为: .
15. 基础建设对社会经济效益产生巨大的作用.某市投入 亿元进行基础建设, 年后产生 亿
元社会经济效益.若该市投资基础建设4年后产生的社会经济效益是投资额的2倍,则再过______年.该
项投资产生的社会经济效益是投资额的8倍.
【答案】8
【解析】
【分析】由4年后产生的社会经济效益是投资额的2倍,代入已知函数式求得参数 ,再求得社会经济效
益是投资额的8倍时的时间 , 即为所求结论.
学科网(北京)股份有限公司【详解】由条件得 ,∴ ,即 .设投资 年后,产生的社会经济效益是投
资额的8倍,则有 ,解得, .
的
所以再过 年,该项投资产生 社会经济效益是投资额的8倍.
故答案为:8.
16. 已知数列的前 的前n项和为 ,数列的 的前n项和为 ,则满足
的最小n的值为______.
【答案】9
【解析】
【详解】 由数列 的前 项和为 ,则当 时, ,
所以 ,
所以数列 的前 和为 ,
当 时, ,
当 时, ,
所以满足 的最小 的值为 .
点睛:本题主要考查了等差数列与等比数列的综合应用问题,其中解答中涉及到数列的通项 与 的
关系,推导数列的通项公式,以及等差、等比数列的前 项和公式的应用,熟记等差、等比数列的通项
公式和前 项和公式是解答的关键,着重考查了学生的推理与运算能力.
四.解答题:本大题共6小题,满分70分. 解答须写出文字说明、证明过程和演算步骤.
17. 已知直线 经过两条直线 和 的交点,且与直线 垂直.
(1)求直线 的一般式方程;
学科网(北京)股份有限公司(2)若圆 的圆心为点 ,直线 被该圆所截得的弦长为 ,求圆 的标准方程.
【答案】(1)
(2)
【解析】
【分析】(1)由题意求出两直线的交点,再求出所求直线的斜率,用点斜式写出直线 的方程;
(2)根据题意求出圆的半径,由圆心写出圆的标准方程.
【小问1详解】
解:由题意知 ,解得 ,
直线 和 的交点为 ;
设直线 的斜率为 , 与直线 垂直, ;
直线 的方程为 ,化为一般形式为 ;
【小问2详解】
解:设圆 的半径为 ,则圆心为 到直线 的距离为
,由垂径定理得 ,
解得 ,
圆 的标准方程为 .
18. 已知 的三个内角 , , 的对边分别为 , , ,且满足 .
(1)求角 的大小;
(2)若 , , ,求 的长.
【答案】(1) ;(2) .
【解析】
学科网(北京)股份有限公司【分析】(1)由正弦定理化边为角后,结合两角和的正弦公式、诱导公式可求得 ;
(2)用 表示出 ,然后平方由数量积的运算求得向量的模(线段长度).
【详解】(1)因为 ,
所以由正弦定理可得 ,
即 ,
因为 ,所以 , ,
∵ ,故 ;
(2)由 ,得 ,
所以 ,
所以 .
19. 已知数列 ,若_________________.
(1)求数列 的通项公式;
(2)求数列 的前 项和 .
从下列三个条件中任选一个补充在上面的横线上,然后对题目进行求解.
① ;
② , , ;
③ ,点 , 在斜率是2的直线上.
【答案】答案见解析.
【解析】
学科网(北京)股份有限公司【分析】(1)若选①,根据通项公式与前 项和的关系求解通项公式即可;
若选②,根据 可得数列 为等差数列,利用基本量法求解通项公式即
可;
若选③,根据两点间的斜率公式可得 ,可得数列 为等差数列进而求得通项公式;
(2)利用裂项相消求和即可
【详解】解:(1)若选①,由 ,
所以当 , ,
两式相减可得: ,
而在 中,令 可得: ,符合上式,
故 .
若选②,由 ( , )可得:数列 为等差数列,
又因为 , ,所以 ,即 ,
所以 .
若选③,由点 , 在斜率是2的直线上得: ,
即 ,
所以数列 为等差数列且 .
(2)由(1)知: ,
所以
.
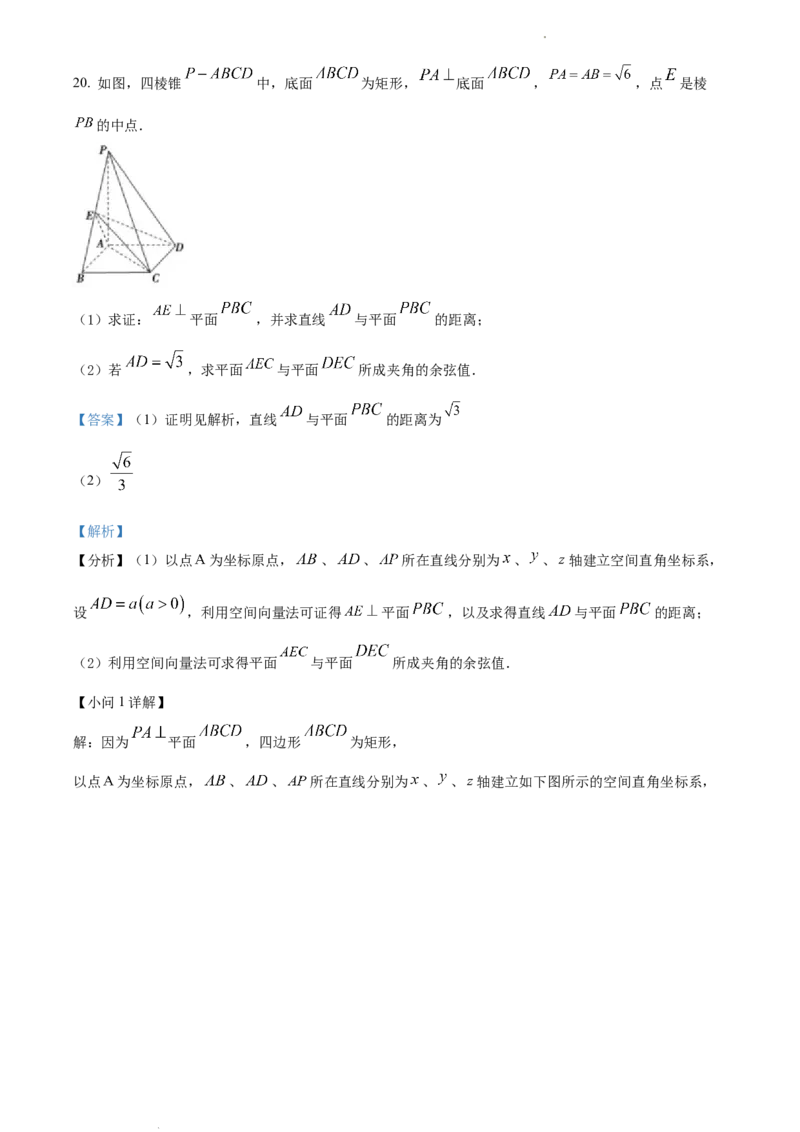
学科网(北京)股份有限公司20. 如图,四棱锥 中,底面 为矩形, 底面 , ,点 是棱
的中点.
(1)求证: 平面 ,并求直线 与平面 的距离;
(2)若 ,求平面 与平面 所成夹角的余弦值.
【答案】(1)证明见解析,直线 与平面 的距离为
(2)
【解析】
【分析】(1)以点 为坐标原点, 、 、 所在直线分别为 、 、 轴建立空间直角坐标系,
设 ,利用空间向量法可证得 平面 ,以及求得直线 与平面 的距离;
(2)利用空间向量法可求得平面 与平面 所成夹角的余弦值.
【小问1详解】
解:因为 平面 ,四边形 为矩形,
以点 为坐标原点, 、 、 所在直线分别为 、 、 轴建立如下图所示的空间直角坐标系,
学科网(北京)股份有限公司设 ,则 、 、 、 、 、
,
, , , ,
所以, , ,
所以, , ,又因为 ,因此, 平面 .
所以,平面 的一个法向量为 ,
, 平面 , 平面 ,则 平面 ,
所以,直线 到平面 的距离为 .
【小问2详解】
解:若 ,则 、 ,
设平面 的法向量为 , , ,
学科网(北京)股份有限公司则 ,取 ,可得 ,
设平面 的法向量为 , , ,
则 ,取 ,可得 ,
.
因此,平面 与平面 所成夹角的余弦值为 .
21. 习近平总书记指出:“我们既要绿水青山,也要金山银山.”新能源汽车环保、节能,以电代油,减少
排放,既符合我国的国情,也代表了世界汽车产业发展的方向.工业部表示,到2025年中国的汽车总销量
将达到3500万辆,并希望新能源汽车至少占总销量的五分之一.江苏某新能源公司年初购入一批新能源汽
车充电桩,每台16200元,第一年每台设备的维修保养费用为1100元,以后每年增加400元,每台充电桩
每年可给公司收益8100元.
(1)每台充电桩第几年开始获利?
(2)每台充电桩在第几年时,年平均利润最大.
【答案】(1)公司从第3年开始获利;(2)第9年时每台充电桩年平均利润最大3600元
【解析】
【分析】(1)判断已知条件是等差数列,然后求解利润的表达式,推出表达式求解n即可.
(2)利用基本不等式求解最大值即可.
【详解】(1)每年的维修保养费用是以1100为首项,400为公差的等差数列,
设第n年时累计利润为f(n),
f(n)=8100n-[1100+1500+…+(400n+700)]-16200
=8100n-n(200n+900)-16200
=-200n2+7200n-16200
=-200(n2-36n+81),
开始获利即f(n)>0,
∴-200(n2-36n+81)>0,即n2-36n+81<0,
学科网(北京)股份有限公司解得 ,
所以公司从第3年开始获利;
(2)每台充电桩年平均利润为
当且仅当 ,即n=9时,等号成立.
即在第9年时每台充电桩年平均利润最大3600元.
【点睛】本题考查数列与函数的实际应用,基本不等式的应用,考查转化思想以及计算能力,是中档题.
22. 已知椭圆 的离心率为 ,点 在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知直线 与椭圆C交于P,Q两点,点M是线段PQ的中点,直线 过点
M,且与直线l垂直.记直线 与y轴的交点为N,求 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)求出 后可得椭圆的方程.
(2)联立直线 的方程和椭圆方程,消去 后利用韦达定理可用 表示 ,利用换元法和二次函数的
性质可求 的取值范围.
【
小问1详解】
学科网(北京)股份有限公司由题意可得 ,解得 , .
故椭圆C的标准方程为 .
【小问2详解】
设 , , .
联立 ,整理得 ,
则 ,解得 ,
从而 , .
因为M是线段PQ的中点,所以 ,
则 ,故 .
直线 的方程为 ,即 .
令 ,得 ,则 ,
所以 .
设 ,则 ,
学科网(北京)股份有限公司故 .
因为 ,所以 ,所以 .
学科网(北京)股份有限公司