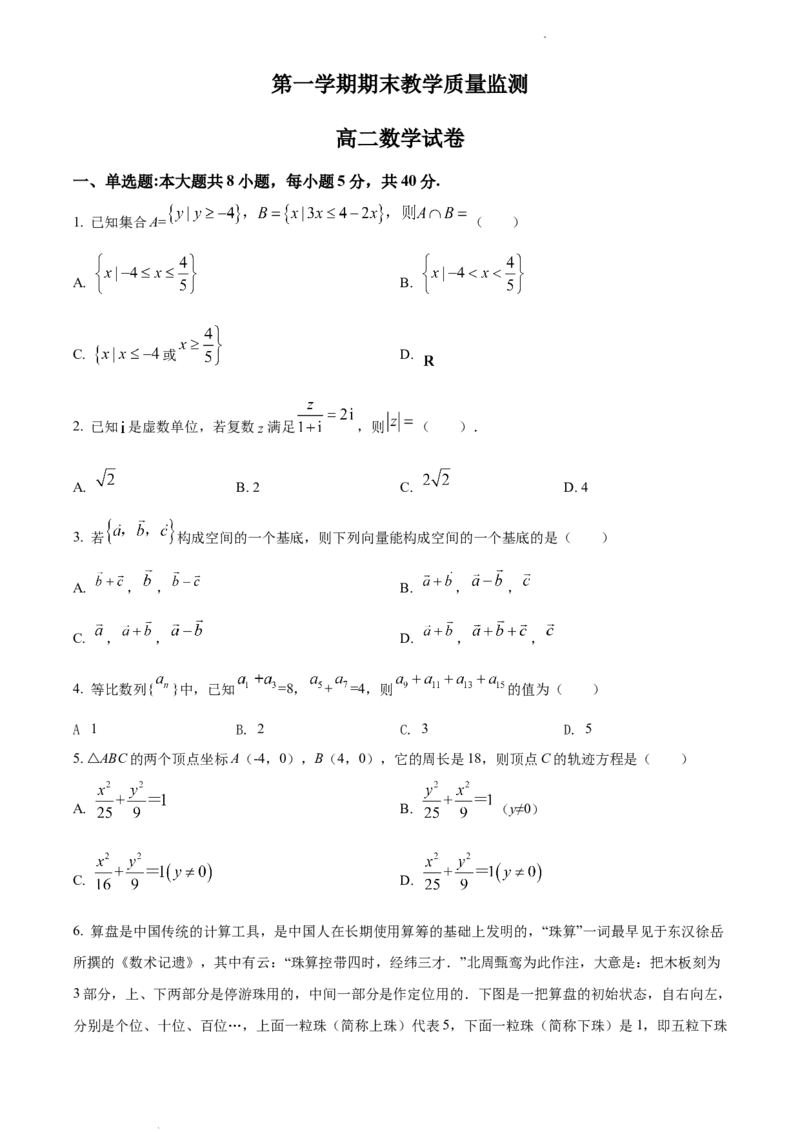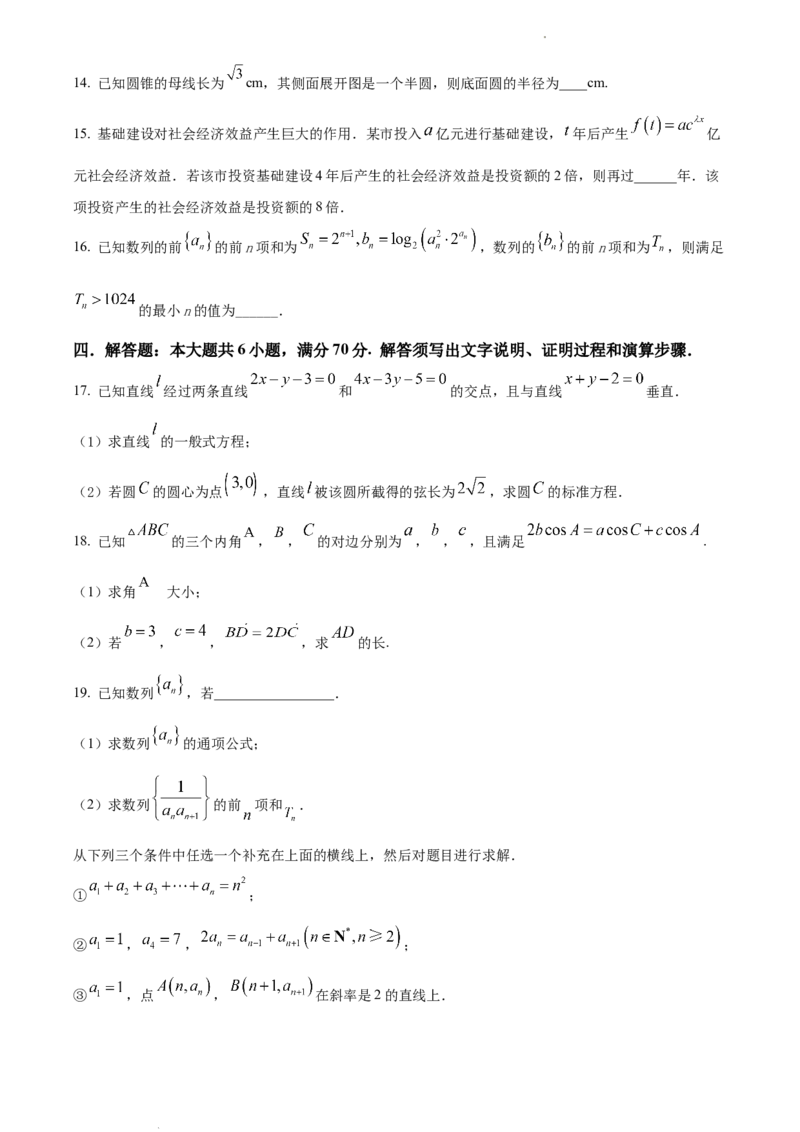文档内容
第一学期期末教学质量监测
高二数学试卷
一、单选题:本大题共8小题,每小题5分,共40分.
1. 已知集合A= ( )
A. B.
C. 或 D.
2. 已知 是虚数单位,若复数 满足 ,则 ( ).
A. B. 2 C. D. 4
3. 若 构成空间的一个基底,则下列向量能构成空间的一个基底的是( )
A. , , B. , ,
C. , , D. , ,
4. 等比数列{ }中,已知 =8, + =4,则 的值为( )
.
A 1 B. 2 C. 3 D. 5
5. △ABC的两个顶点坐标A(-4,0),B(4,0),它的周长是18,则顶点C的轨迹方程是( )
A. B. (y≠0)
C. D.
6. 算盘是中国传统的计算工具,是中国人在长期使用算筹的基础上发明的,“珠算”一词最早见于东汉徐岳
所撰的《数术记遗》,其中有云:“珠算控带四时,经纬三才.”北周甄鸾为此作注,大意是:把木板刻为
3部分,上、下两部分是停游珠用的,中间一部分是作定位用的.下图是一把算盘的初始状态,自右向左,
分别是个位、十位、百位…,上面一粒珠(简称上珠)代表5,下面一粒珠(简称下珠)是1,即五粒下珠
学科网(北京)股份有限公司的大小等于同组一粒上珠的大小.现在从个位和十位这两组中随机选择往下拨一粒上珠,往上拨3粒下珠,
得到的数为质数(除了1和本身没有其它的约数)的概率是( )
A. B. C. D.
7. 直线 分别与 轴, 轴交于 , 两点,点 在圆 上,则 面积
的取值范围是
A. B. C. D.
8. 已知 , 是球 的球面上两点, , 为该球面上的动点,若三棱锥 体积的
最大值为36,则球 的表面积为( )
.
A B. C. D.
二、多选题:本大题共4小题,共20分.在每小题给出的选项中,有多个符合题目要求.全部选
对的得5分,有选错的得0分,部分选对的得2分.
9. 已知数列 满足 , ,则下列各数是 的项的有( )
A. B. C. D.
10. 血压(bloodpressure,BP)是指血液在血管内流动时作用于单位面积血管壁的侧压力,它是推动血液
在血管内流动的动力,血压的最大值、最小值分别称为收缩压和舒张压.未使用抗高血压药的前提下,18岁
以上成人收缩压 或舒张压 ,则说明这位成人有高血压,设从未使用抗高血压药
学科网(北京)股份有限公司的李华今年40岁,从某天早晨6点开始计算(即早晨6点时, ),他的血压 ( )与经
过的时间 ( )满足关系式 ,则( )
A. 函数 的最小正周期为6 B. 当天早晨7点时李华的血压为
C. 当天李华有高血压 D. 当天李华的收缩压与舒张压之差为
11. 已知动点 在双曲线 上,双曲线 左的、右焦点分别为 、 ,下列结论正确的是(
)
的
A. 离心率为
B. 的渐近线方程为
C. 动点 到两条渐近线的距离之积为定值
D. 当动点 在双曲线 的左支上时, 的最大值为
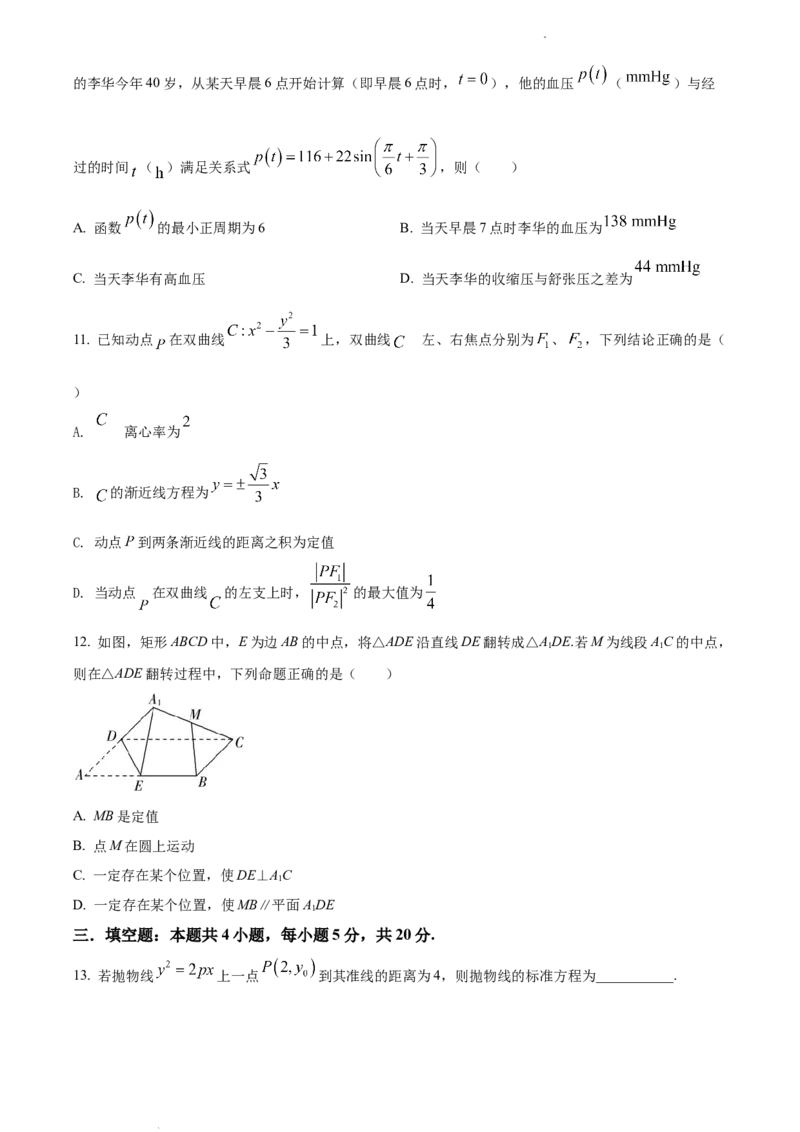
12. 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△ADE.若M为线段AC的中点,
1 1
则在△ADE翻转过程中,下列命题正确的是( )
A. MB是定值
B. 点M在圆上运动
C. 一定存在某个位置,使DE⊥AC
1
D. 一定存在某个位置,使MB∥平面ADE
1
三.填空题:本题共4小题,每小题5分,共20分.
13. 若抛物线 上一点 到其准线的距离为4,则抛物线的标准方程为___________.
学科网(北京)股份有限公司14. 已知圆锥的母线长为 cm,其侧面展开图是一个半圆,则底面圆的半径为____cm.
15. 基础建设对社会经济效益产生巨大的作用.某市投入 亿元进行基础建设, 年后产生 亿
元社会经济效益.若该市投资基础建设4年后产生的社会经济效益是投资额的2倍,则再过______年.该
项投资产生的社会经济效益是投资额的8倍.
16. 已知数列的前 的前n项和为 ,数列的 的前n项和为 ,则满足
的最小n的值为______.
四.解答题:本大题共6小题,满分70分. 解答须写出文字说明、证明过程和演算步骤.
17. 已知直线 经过两条直线 和 的交点,且与直线 垂直.
(1)求直线 的一般式方程;
(2)若圆 的圆心为点 ,直线 被该圆所截得的弦长为 ,求圆 的标准方程.
18. 已知 的三个内角 , , 的对边分别为 , , ,且满足 .
的
(1)求角 大小;
(2)若 , , ,求 的长.
19. 已知数列 ,若_________________.
(1)求数列 的通项公式;
(2)求数列 的前 项和 .
从下列三个条件中任选一个补充在上面的横线上,然后对题目进行求解.
① ;
② , , ;
③ ,点 , 在斜率是2的直线上.
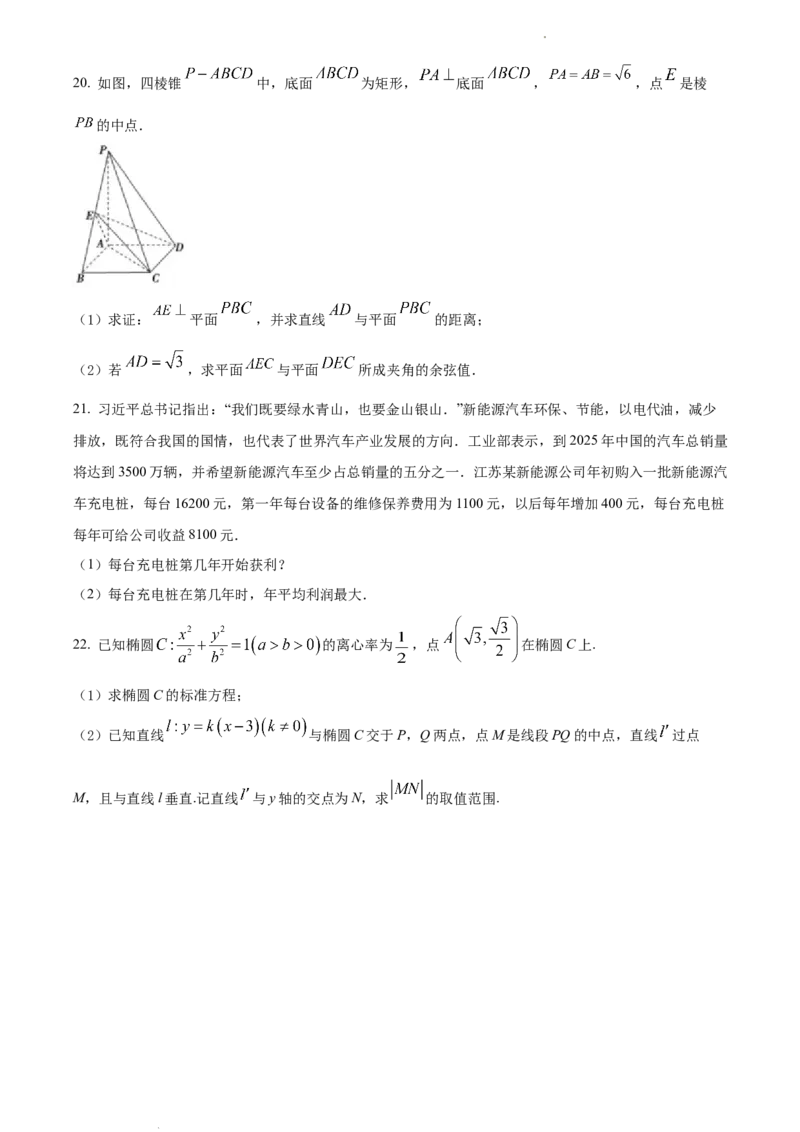
学科网(北京)股份有限公司20. 如图,四棱锥 中,底面 为矩形, 底面 , ,点 是棱
的中点.
(1)求证: 平面 ,并求直线 与平面 的距离;
(2)若 ,求平面 与平面 所成夹角的余弦值.
21. 习近平总书记指出:“我们既要绿水青山,也要金山银山.”新能源汽车环保、节能,以电代油,减少
排放,既符合我国的国情,也代表了世界汽车产业发展的方向.工业部表示,到2025年中国的汽车总销量
将达到3500万辆,并希望新能源汽车至少占总销量的五分之一.江苏某新能源公司年初购入一批新能源汽
车充电桩,每台16200元,第一年每台设备的维修保养费用为1100元,以后每年增加400元,每台充电桩
每年可给公司收益8100元.
(1)每台充电桩第几年开始获利?
(2)每台充电桩在第几年时,年平均利润最大.
22. 已知椭圆 的离心率为 ,点 在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知直线 与椭圆C交于P,Q两点,点M是线段PQ的中点,直线 过点
M,且与直线l垂直.记直线 与y轴的交点为N,求 的取值范围.
学科网(北京)股份有限公司