文档内容
期末数学试卷
(时间:120分钟 满分:150分)
注意事项:1.答题前在答题卷上填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卷上.
一、选择题(每小题5分,共60分.注意:9至12题为多选题.)
1. 过点 , 的直线的斜率等于1,则m的值为( )
A. 1 B. 4 C. 1或3 D. 1或4
2. 若圆 的半径为 ,则实数 ( )
A. B. -1 C. 1 D.
3. 已知A,B,C三点不共线,O是平面ABC外一点,下列条件中能确定点M与点A,B,C一定共面的是
A. B.
C. D.
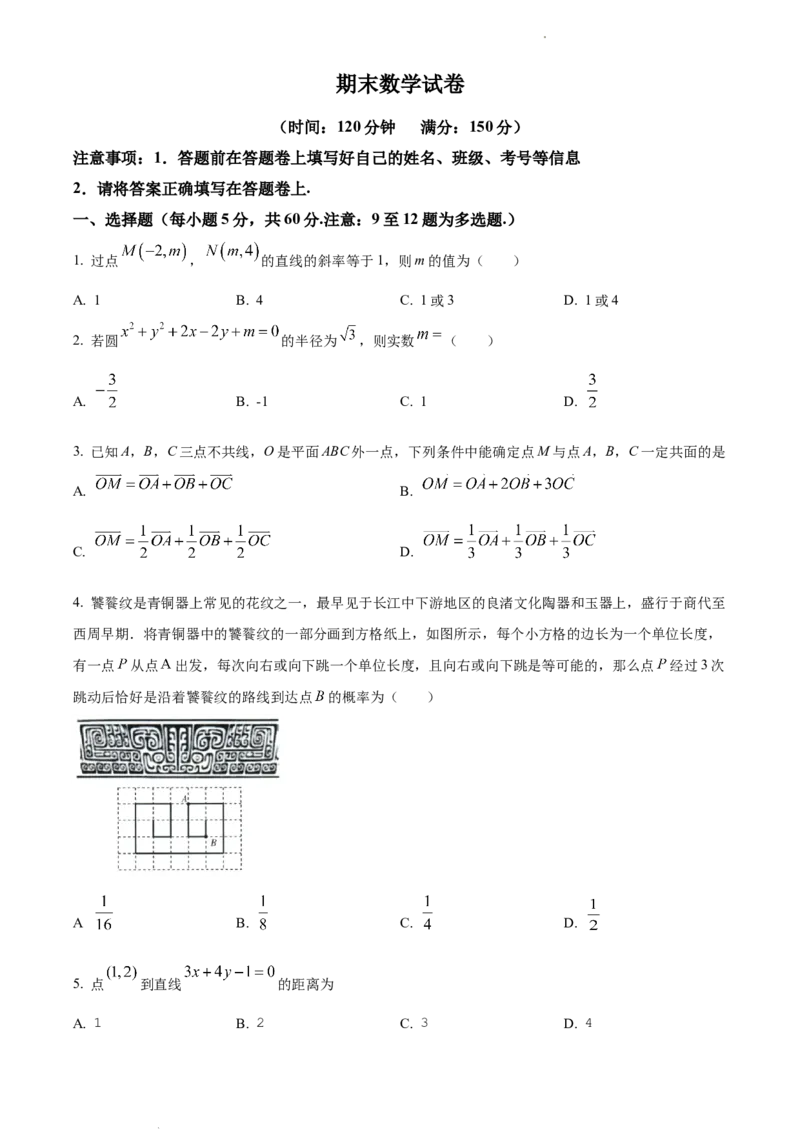
4. 饕餮纹是青铜器上常见的花纹之一,最早见于长江中下游地区的良渚文化陶器和玉器上,盛行于商代至
西周早期.将青铜器中的饕餮纹的一部分画到方格纸上,如图所示,每个小方格的边长为一个单位长度,
有一点 从点 出发,每次向右或向下跳一个单位长度,且向右或向下跳是等可能的,那么点 经过3次
跳动后恰好是沿着饕餮纹的路线到达点 的概率为( )
.
A B. C. D.
5. 点 到直线 的距离为
A. 1 B. 2 C. 3 D. 4
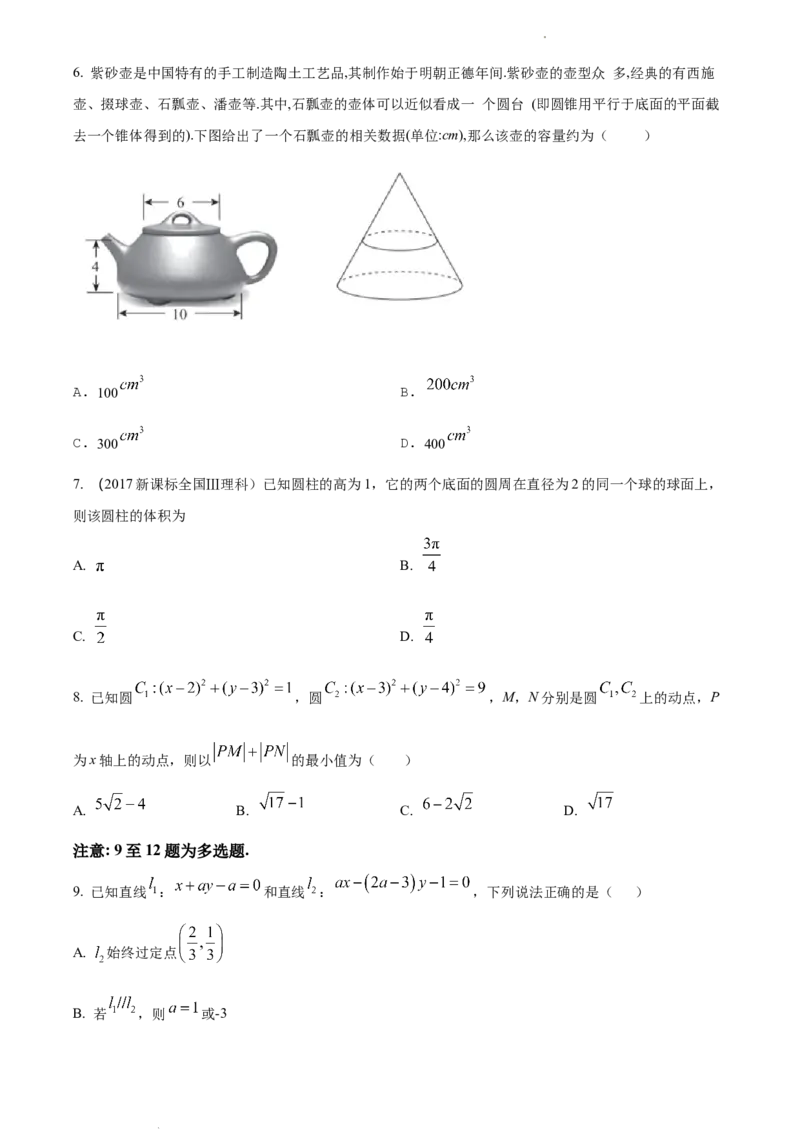
学科网(北京)股份有限公司6. 紫砂壶是中国特有的手工制造陶土工艺品,其制作始于明朝正德年间.紫砂壶的壶型众 多,经典的有西施
壶、掇球壶、石瓢壶、潘壶等.其中,石瓢壶的壶体可以近似看成一 个圆台 (即圆锥用平行于底面的平面截
去一个锥体得到的).下图给出了一个石瓢壶的相关数据(单位:cm),那么该壶的容量约为( )
A. 100 B.
C. 300 D. 400
7. (2017新课标全国Ⅲ理科)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,
则该圆柱的体积为
A. B.
C. D.
8. 已知圆 ,圆 ,M,N分别是圆 上的动点,P
为x轴上的动点,则以 的最小值为( )
A. B. C. D.
注意: 9至12题为多选题.
9. 已知直线 : 和直线 : ,下列说法正确的是( )
A. 始终过定点
B. 若 ,则 或-3
学科网(北京)股份有限公司C. 若 ,则 或2
.
D 当 时, 始终不过第三象限
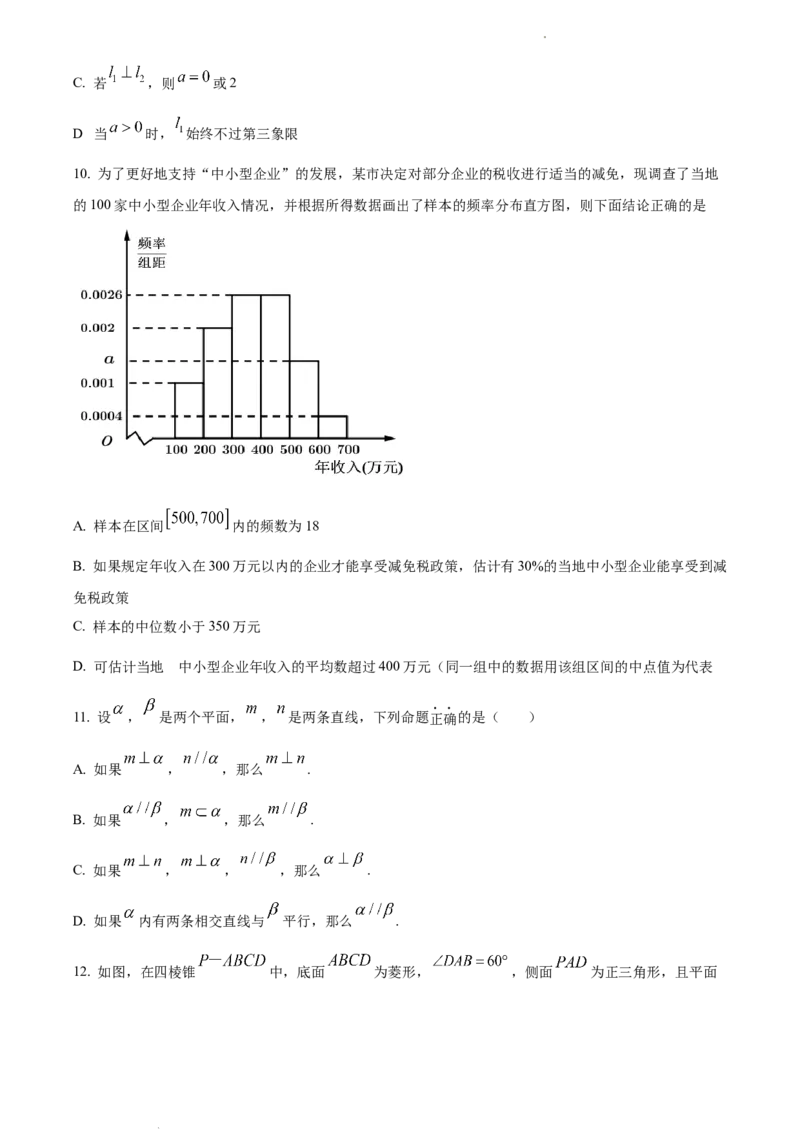
10. 为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,现调查了当地
的100家中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,则下面结论正确的是
A. 样本在区间 内的频数为18
B. 如果规定年收入在300万元以内的企业才能享受减免税政策,估计有30%的当地中小型企业能享受到减
免税政策
C. 样本的中位数小于350万元
的
D. 可估计当地 中小型企业年收入的平均数超过400万元(同一组中的数据用该组区间的中点值为代表
11. 设 , 是两个平面, , 是两条直线,下列命题正确的是( )
A. 如果 , ,那么 .
B. 如果 , ,那么 .
C. 如果 , , ,那么 .
D. 如果 内有两条相交直线与 平行,那么 .
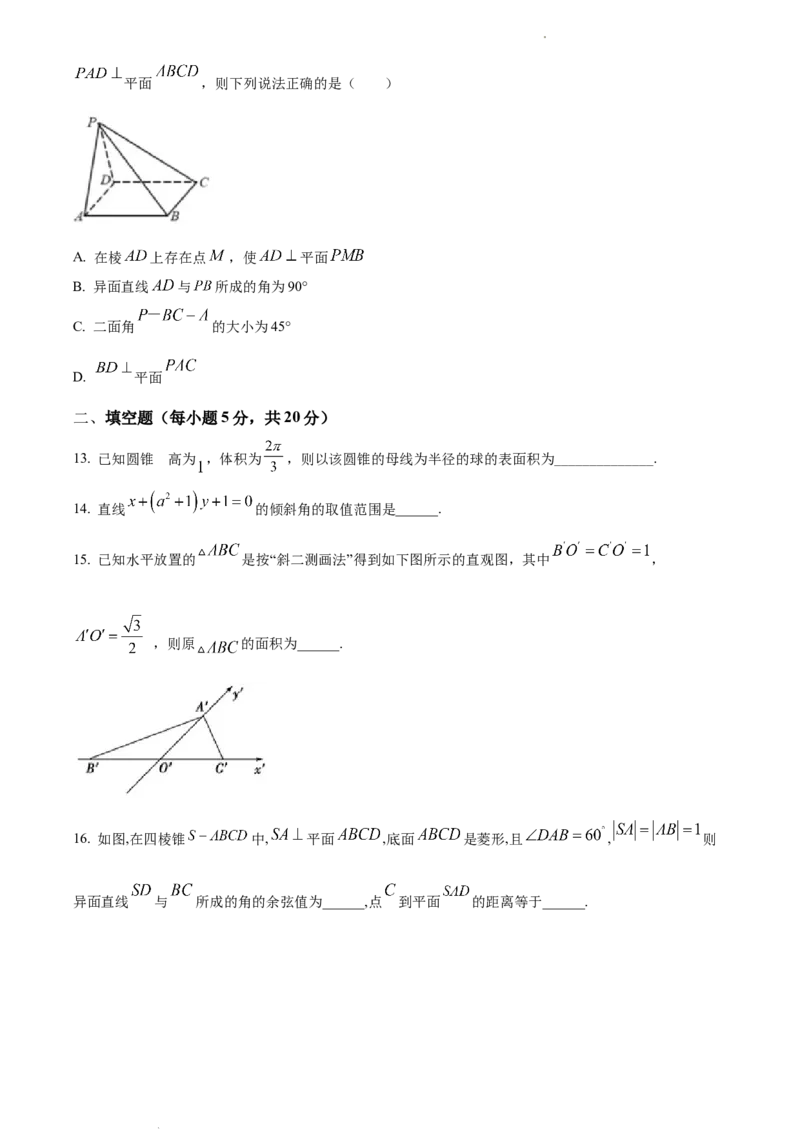
12. 如图,在四棱锥 中,底面 为菱形, ,侧面 为正三角形,且平面
学科网(北京)股份有限公司平面 ,则下列说法正确的是( )
A. 在棱 上存在点 ,使 平面
B. 异面直线 与 所成的角为90°
C. 二面角 的大小为45°
D. 平面
二、填空题(每小题5分,共20分)
13. 已知圆锥 高为 ,体积为 ,则以该圆锥的母线为半径的球的表面积为______________.
的
14. 直线 的倾斜角的取值范围是______.
15. 已知水平放置的 是按“斜二测画法”得到如下图所示的直观图,其中 ,
,则原 的面积为______.
16. 如图,在四棱锥 中, 平面 ,底面 是菱形,且 , 则
异面直线 与 所成的角的余弦值为______,点 到平面 的距离等于______.
学科网(北京)股份有限公司三、解答题(共70分.注意:以一定的文字说明并规范答题)
17. 已知向量 , .
(1)计算 和 ;
(2)求 .
18. 已知三角形的三个顶点是 , , .
(1)求 边上的中线所在直线的方程;
(2)求 边上的高所在直线的方程.
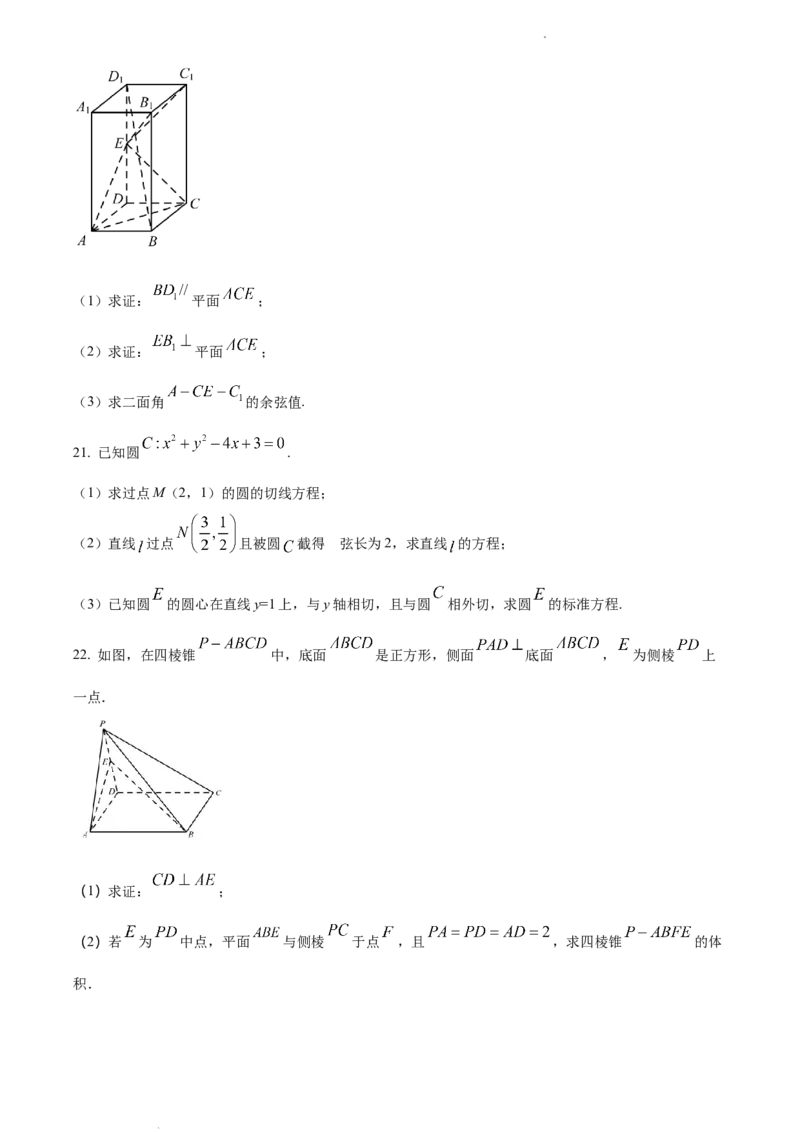
19. 某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低
于40分的整数)分成六段: , ,…, 所得到如图所示的频率分布直图
(1)求图中实数 的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这2名学生的数学
成绩之差的绝对值不大于10的概率.
20. 如图长方体 中, , ,点 为 的中点.
学科网(北京)股份有限公司(1)求证: 平面 ;
(2)求证: 平面 ;
(3)求二面角 的余弦值.
21. 已知圆 .
(1)求过点M(2,1)的圆的切线方程;
(2)直线 过点 且被圆 截得 弦的长为2,求直线 的方程;
(3)已知圆 的圆心在直线y=1上,与y轴相切,且与圆 相外切,求圆 的标准方程.
22. 如图,在四棱锥 中,底面 是正方形,侧面 底面 , 为侧棱 上
一点.
(1)求证: ;
(2)若 为 中点,平面 与侧棱 于点 ,且 ,求四棱锥 的体
积.
学科网(北京)股份有限公司学科网(北京)股份有限公司