文档内容
常州市教育学会学业水平监测
高三数学
2024年1月
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.
如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡
上.写在本试卷上无效.
3.考试结束后,将答题卡交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.设集合A={x|x2=x},B={x|lnx<0},则A∪B=
A.[0,1] B.(0,1] C.[0,1) D.(0,1)
2.在复平面内,复数z=-+i对应的向量为,复数z+1对应的向量为,那么向量对应的
复数是
A.1 B.-1 C.i D.-i
3.已知实数a,b满足等式lga=lnb,下列三个关系式中可能成立的个数为
①a<b<1;②1<a<b;③a=b.
A.0 B.1 C.2 D.3
4.对任意实数a,b,C,在下列命题中,真命题是
A.“ac2>bc2”是“a>b”的必要条件
B.“ac2=bc2”是“a=b”的必要条件
C.“ac2=bc2”是“a=b”的充分条件
D.“ac2≥bc2”是“a≥b”的充分条件
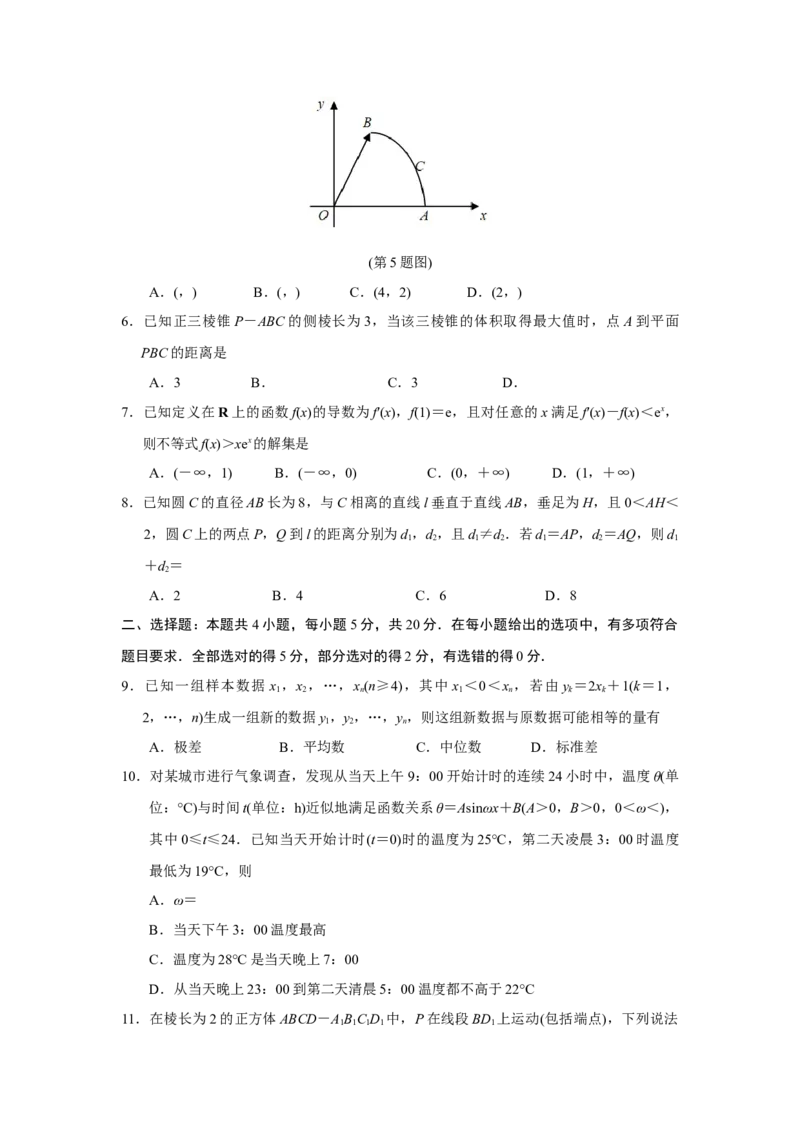
5.已知扇形AOB的半径为5,以O为原点建立如图所示的平面直角坐标系,=(5,0),=
(4,3),弧AB的中点为C,则=(第5题图)
A.(,) B.(,) C.(4,2) D.(2,)
6.已知正三棱锥P-ABC的侧棱长为3,当该三棱锥的体积取得最大值时,点A到平面
PBC的距离是
A.3 B. C.3 D.
7.已知定义在R上的函数f(x)的导数为f′(x),f(1)=e,且对任意的x满足f′(x)-f(x)<ex,
则不等式f(x)>xex的解集是
A.(-∞,1) B.(-∞,0) C.(0,+∞) D.(1,+∞)
8.已知圆C的直径AB长为8,与C相离的直线l垂直于直线AB,垂足为H,且0<AH<
2,圆C上的两点P,Q到l的距离分别为d,d,且d≠d.若d=AP,d=AQ,则d
1 2 1 2 1 2 1
+d=
2
A.2 B.4 C.6 D.8
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知一组样本数据 x ,x ,…,x(n≥4),其中 x <0<x ,若由y =2x +1(k=1,
1 2 n 1 n k k
2,…,n)生成一组新的数据y,y,…,y,则这组新数据与原数据可能相等的量有
1 2 n
A.极差 B.平均数 C.中位数 D.标准差
10.对某城市进行气象调查,发现从当天上午9:00开始计时的连续24小时中,温度θ(单
位:°C)与时间t(单位:h)近似地满足函数关系θ=Asinωx+B(A>0,B>0,0<ω<),
其中0≤t≤24.已知当天开始计时(t=0)时的温度为25°C,第二天凌晨3:00时温度
最低为19°C,则
A.ω=
B.当天下午3:00温度最高
C.温度为28°C是当天晚上7:00
D.从当天晚上23:00到第二天清晨5:00温度都不高于22°C
11.在棱长为2的正方体ABCD-ABC D 中,P在线段BD 上运动(包括端点),下列说法
1 1 1 1 1正确的有
A.存在点P,使得CP⊥平面ADB
1
B.不存在点P,使得直线C P与平面ADB所成的角为30°
1 1
C.PC+PD的最小值为2
D.以P为球心,PA为半径的球体积最小时,被正方形ADD A 截得的弧长是π
1 1
12.关于函数f(x)=,下列说法正确的有
A.函数f(x)的图象关于点(-,0)对称
B.函数f(x)在(-∞,2)上单调递增,在(2,+∞)上单调递减
C.若方程f(x)=t恰有一个实数根,则t=
D.若∀x∈R,都有f(x)>m,则m≤-2
三、填空题:本题共4小题,每小题5分,共20分.
13.已知双曲线的标准方程为,则该双曲线的焦距是 .
14.已知函数f(x)=若f[f()]=a,则实数a的值为 .
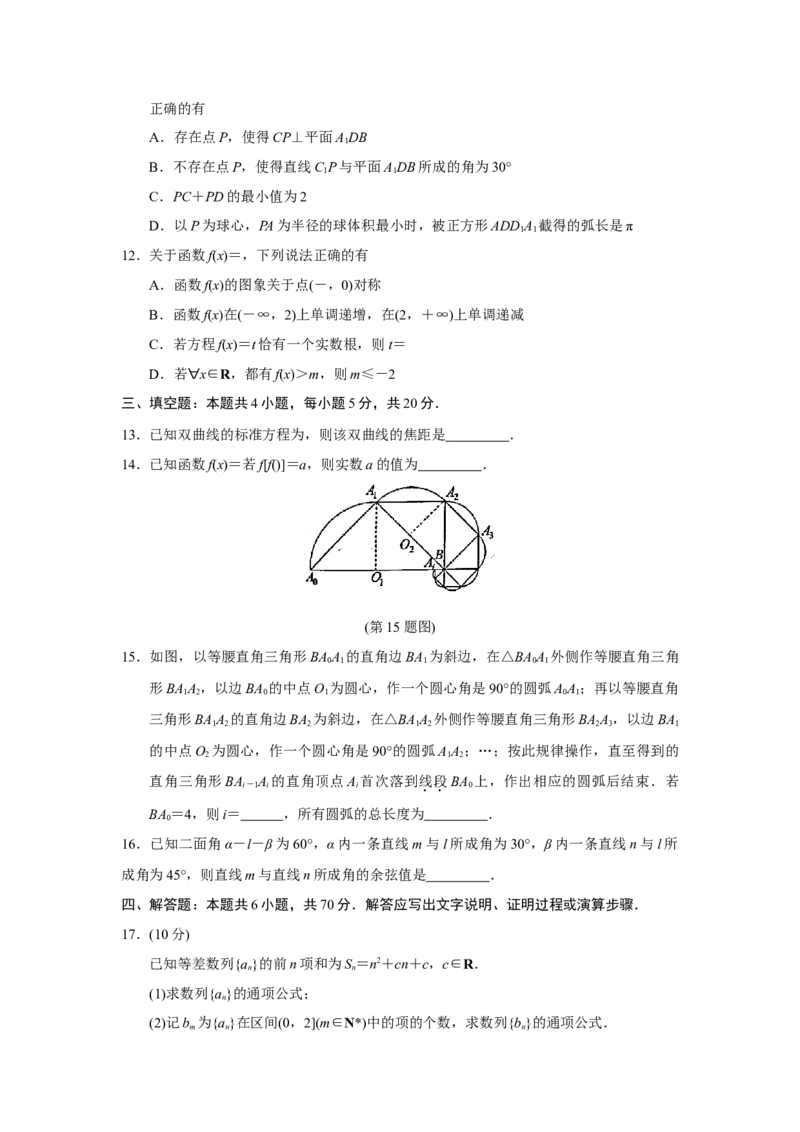
(第15题图)
15.如图,以等腰直角三角形BAA 的直角边BA 为斜边,在△BAA 外侧作等腰直角三角
0 1 1 0 1
形BAA ,以边BA 的中点O 为圆心,作一个圆心角是90°的圆弧AA ;再以等腰直角
1 2 0 1 0 1
三角形BAA 的直角边BA 为斜边,在△BAA 外侧作等腰直角三角形BAA ,以边BA
1 2 2 1 2 2 3 1
的中点O 为圆心,作一个圆心角是90°的圆弧AA ;…;按此规律操作,直至得到的
2 1 2
直角三角形BA A 的直角顶点A 首次落到线段BA 上,作出相应的圆弧后结束.若
i-1 i i 0
BA=4,则i= ,所有圆弧的总长度为 .
0
16.已知二面角α-l-β为60°,α内一条直线m与l所成角为30°,β内一条直线n与l所
成角为45°,则直线m与直线n所成角的余弦值是 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
已知等差数列{a}的前n项和为S=n2+cn+c,c∈R.
n n
(1)求数列{a}的通项公式;
n
(2)记b 为{a}在区间(0,2](m∈N*)中的项的个数,求数列{b}的通项公式.
m n n18.(12分)
某制造商生产的5000根金属棒的长度近似服从正态分布N(6,σ2),其中恰有114根金
属棒长度不小于6.04.
(1)求σ;
(2)如果允许制造商生产这种金属棒的长度范围是(5.95,6.05),那么这批金属棒中不合格的
金属棒约有多少根?
说明:对任何一个正态分布X~N(μ,σ2)来说,通过Z=转化为标准正态分布Z~N(0,
1),从而查标准正态分布表得到P(X<X)= (Z).
1
可供查阅的(部分)Φ标准正态分布表Φ(Z)
Z 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
Φ(Z) 0.8643 0.8849 0.9032 0.9192 0.9332 0.9452 0.9554 0.9641 0.9713
Z 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8
Φ(Z) 0.9772 0.9821 0.9861 0.9893 0.9918 0.9938 0.9953 0.9965 0.9974
19.(12分)
记△ABC的内角A,B,C的对边分别为a,b,c,AC边上的高为h,已知B=.
(1)若b=h,求的值;
(2)若c-a=h,求sinA-cosA的值.20.(12分)
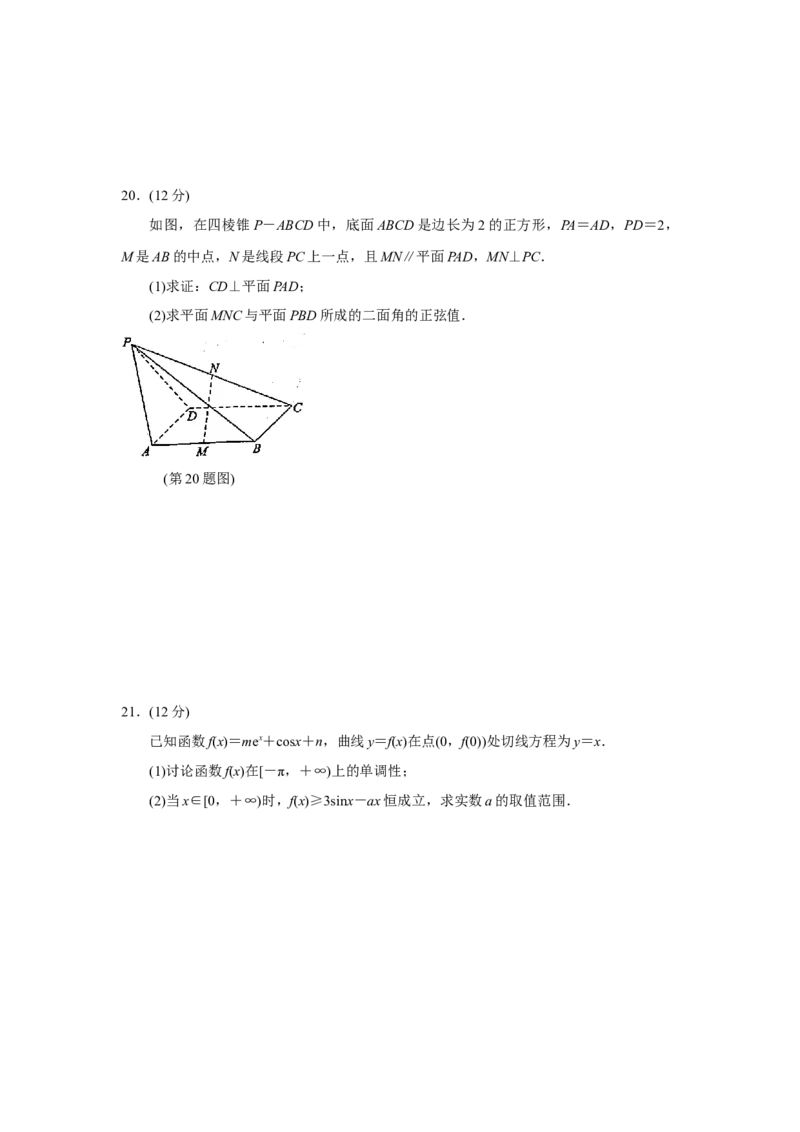
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=AD,PD=2,
M是AB的中点,N是线段PC上一点,且MN∥平面PAD,MN⊥PC.
(1)求证:CD⊥平面PAD;
(2)求平面MNC与平面PBD所成的二面角的正弦值.
(第20题图)
21.(12分)
已知函数f(x)=mex+cosx+n,曲线y=f(x)在点(0,f(0))处切线方程为y=x.
(1)讨论函数f(x)在[-π,+∞)上的单调性;
(2)当x∈[0,+∞)时,f(x)≥3sinx-ax恒成立,求实数a的取值范围.22.(12分)
已知椭圆C:(a>b>0)的左焦点为F,离心率为e,A,B是C上的相异两点,P(2a,
0).
(1)若点A,B关于原点对称,且FA⊥FB,求e的取值范围;
(2)若点A,B关于x轴对称,直线PA交C于另一点D,直线BD与x轴的交点Q的横
坐标为1,过Q的直线交C于M,N两点.已知e=,求·的取值范围.