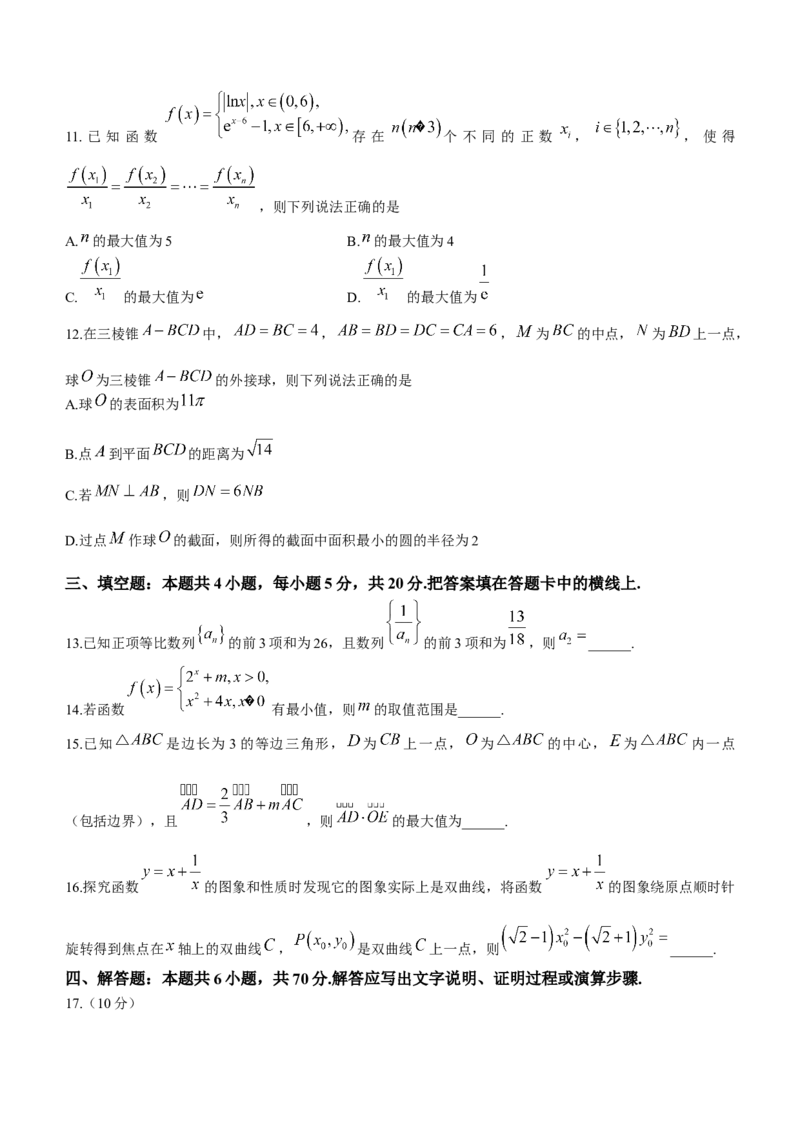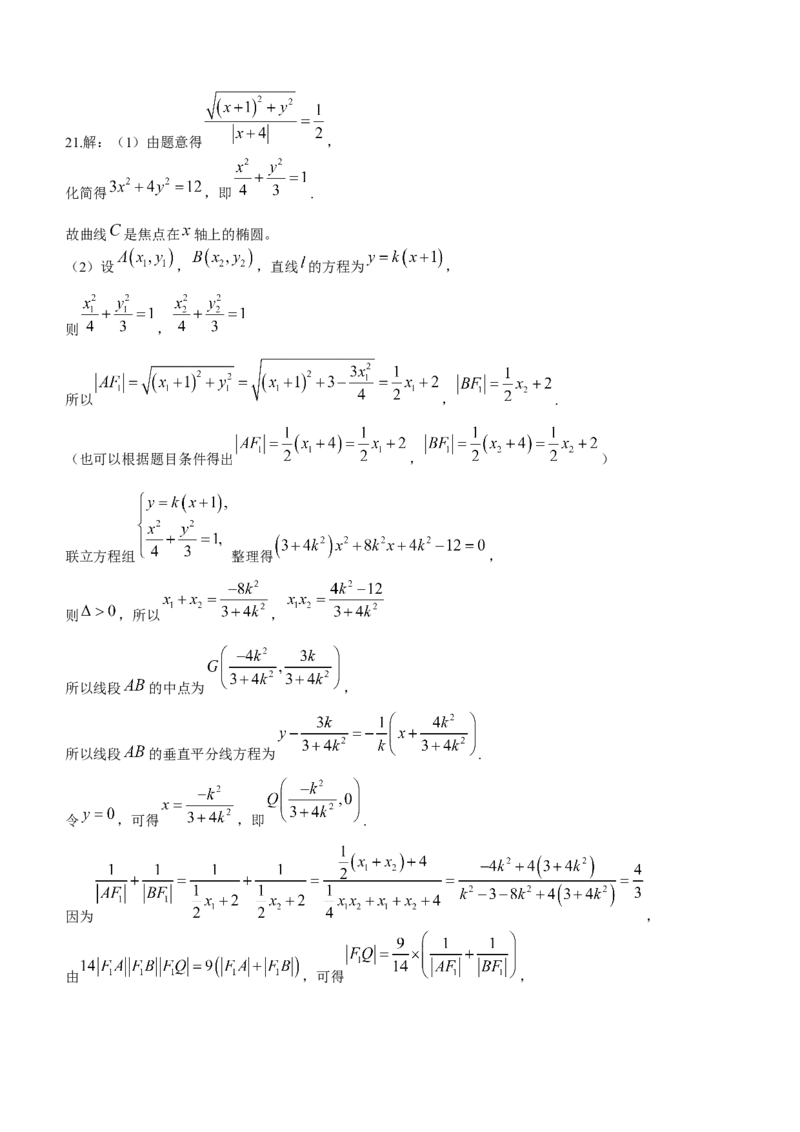文档内容
驻马店市 2023-2024 学年度高三年级期末统一考试
数学
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷
上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.本试卷主要考试内容:高考全部内容。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.设复数 ,则
A. B. C. D.
2.设集合 , ,则
A. B.
C. D.
3.已知函数 的定义域为 ,则 的最小值为
A.1 B.2 C.4 D.5
4.如图,这是某厂生产的一批不倒肦型台灯外形,它由一个圆锥和一个半球组合而成,且圆锥的体积恰好等
于半球的体积,则该圆锥的轴截面的顶角的余弦值为
A. B. C. D.
5.设圆 : 和圆 : 交于 , 两点,则四边形 的面积为
学科网(北京)股份有限公司A. B.4 C.6 D.
6.已知 ,则
A. B. C. D.
7.将5本不同的书(2本文学书、2本科学书和1本体育书)分给甲、乙、丙三人,每人至少分得1本书,每
本书只能分给一人,其中体育书只能分给甲、乙中的一人,则不同的分配方法数为
A.78 B.92 C.100 D.122
8.已知 为坐标原点,抛物线 : 的焦点为 ,过点 的直线 交抛物线 于 , 两点,若
,则
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.为了解高三学生体能情况,某中学对所有高三男生进行了1000米跑测试,测试结果表明所有男生的成绩
(单位:分)近似服从正态分布 , , ,则下列说法正确的是
A.若从高三男生中随机挑选1人,则他的成绩在 内的概率为0.2
B.若从高三男生中随机挑选1人,则他的成绩在 内的概率为0.4
C.若从高三男生中随机挑选2人,则他们的成绩都不低于75的概率为0.25
D. 越大, 的值越小
10.将函数 的图象向右平移 个单位长度,再将所得的图象关于 轴对称,得到函数 的
图象,则下列结论正确的是
A. 的图象关于点 对称 B. 在 上的值域为
C. 为偶函数 D. 在 上单调递增
学科网(北京)股份有限公司11. 已 知 函 数 存 在 个 不 同 的 正 数 , , 使 得
,则下列说法正确的是
A. 的最大值为5 B. 的最大值为4
C. 的最大值为 D. 的最大值为
12.在三棱锥 中, , , 为 的中点, 为 上一点,
球 为三棱锥 的外接球,则下列说法正确的是
A.球 的表面积为
B.点 到平面 的距离为
C.若 ,则
D.过点 作球 的截面,则所得的截面中面积最小的圆的半径为2
三、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.
13.已知正项等比数列 的前3项和为26,且数列 的前3项和为 ,则 ______.
14.若函数 有最小值,则 的取值范围是______.
15.已知 是边长为3的等边三角形, 为 上一点, 为 的中心, 为 内一点
(包括边界),且 ,则 的最大值为______.
16.探究函数 的图象和性质时发现它的图象实际上是双曲线,将函数 的图象绕原点顺时针
旋转得到焦点在 轴上的双曲线 , 是双曲线 上一点,则 ______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
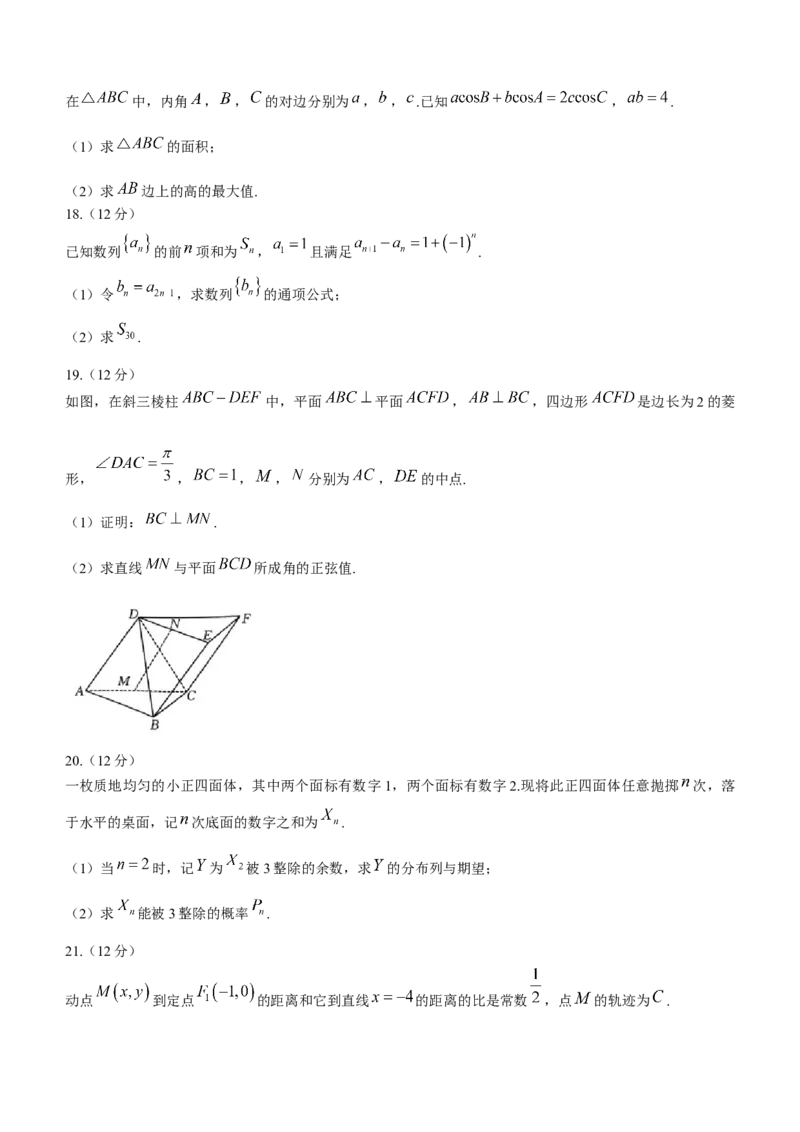
学科网(北京)股份有限公司在 中,内角 , , 的对边分别为 , , .已知 , .
(1)求 的面积;
(2)求 边上的高的最大值.
18.(12分)
已知数列 的前 项和为 , 且满足 .
(1)令 ,求数列 的通项公式;
(2)求 .
19.(12分)
如图,在斜三棱柱 中,平面 平面 , ,四边形 是边长为2的菱
形, , , , 分别为 , 的中点.
(1)证明: .
(2)求直线 与平面 所成角的正弦值.
20.(12分)
一枚质地均匀的小正四面体,其中两个面标有数字1,两个面标有数字2.现将此正四面体任意抛掷 次,落
于水平的桌面,记 次底面的数字之和为 .
(1)当 时,记 为 被3整除的余数,求 的分布列与期望;
(2)求 能被3整除的概率 .
21.(12分)
动点 到定点 的距离和它到直线 的距离的比是常数 ,点 的轨迹为 .
学科网(北京)股份有限公司(1)求 的方程,并说明 是什么曲线;
(2)过点 作不与坐标轴垂直的直线 交 于 , 两点,线段 的垂直平分线与 轴交于点 ,若
,求 的方程.
22.(12分)
已知函数 有两个零点.
(1)求 的取值范围;
(2)设 , 是 的两个零点, ,证明: .
学科网(北京)股份有限公司驻马店市 2023-2024 学年度高三年级期末统一考试
数学参考答案
1.B ,则 .
2.A 依题得 ,则 .
3.C 由题可知 ,且 ,即 ,所以 ,当且仅当 , 时,等
号成立,则 的最小值为4.
4.C 几何体的轴截面如图所示,设圆锥的底面半径为 ,高为 ,母线长为 ,则球的半径也为 .因为圆锥
的体积恰好等于半球的体积,所以 ,得 .故 .设圆锥的轴截
面的顶角为 ,则 .
5.B 由题意可知 , ,直线 的方程为 ,易知四边形 为菱形,所
以 到 直 线 的 距 离 , 所 以 , 故
.
6.A
学科网(北京)股份有限公司.
7.C 若 将 体 育 书 分 给 甲 , 当 剩 余 4 本 书 恰 好 分 给 乙 、 丙 时 , 此 时 的 分 配 方 法 有
种,当剩余 4 本书恰好分给甲、乙、丙三人时,此时的分配方法有
种.综上,将体育书分给甲,不同的分配方法数是 .
同理,将体育书分给乙,不同的分配方法数也是50.故不同的分配方法数是 .
8.D 不妨设点 在第一象限,直线 的倾斜角为 ,所以 ,则 ,同理可
得 . 因 为 , 所 以 , 即 , , 所 以
.
在 中, .
9.ABC ,
,故A,B正确.无论 为何值, ,若从高三男生中
随机挑选2人,则他们的成绩都不低于75的概率为 ,故C正确,D错误.
10.BCD 由题得, ,
令 ,则 , ,故A错误;
当 时, , ,故B正确;
为偶函数,故C正确;
学科网(北京)股份有限公司当 时, ,所以 在 上单调递增,故D正确.
11.BD 的 几 何 意 义 为 过 点 , 的 直 线 的 斜 率 . 易 知 直 线 与
的图象最多只有4个交点,故 的最大值为4.当直线 与曲线 相切
时, 取得最大值,设切点为 ,则该直线的斜率为 ,又 ,所以 ,
解得 ,得 ,所以 .
12.BCD 由 , ,可将三棱锥 补形成如图所示的长方体,
则 , ,所以球 的半径为 ,所以球 的
表面积为 ,故A错误.易知 平面 ,过点 作 的垂线,交 于 ,故 为点 到
平面 的距离.在 中, , ,解得 ,故B正确.以 为原点,
, , 所 在 直 线 分 别 为 , , 轴 建 立 空 间 直 角 坐 标 系 , 则
, , , ,
. 设 , 所 以
. 因 为 , 所 以
,解得 ,所以 ,故C正确.当且仅当 与截面
垂直时,截面面积最小,最小的半径为2,故D正确.
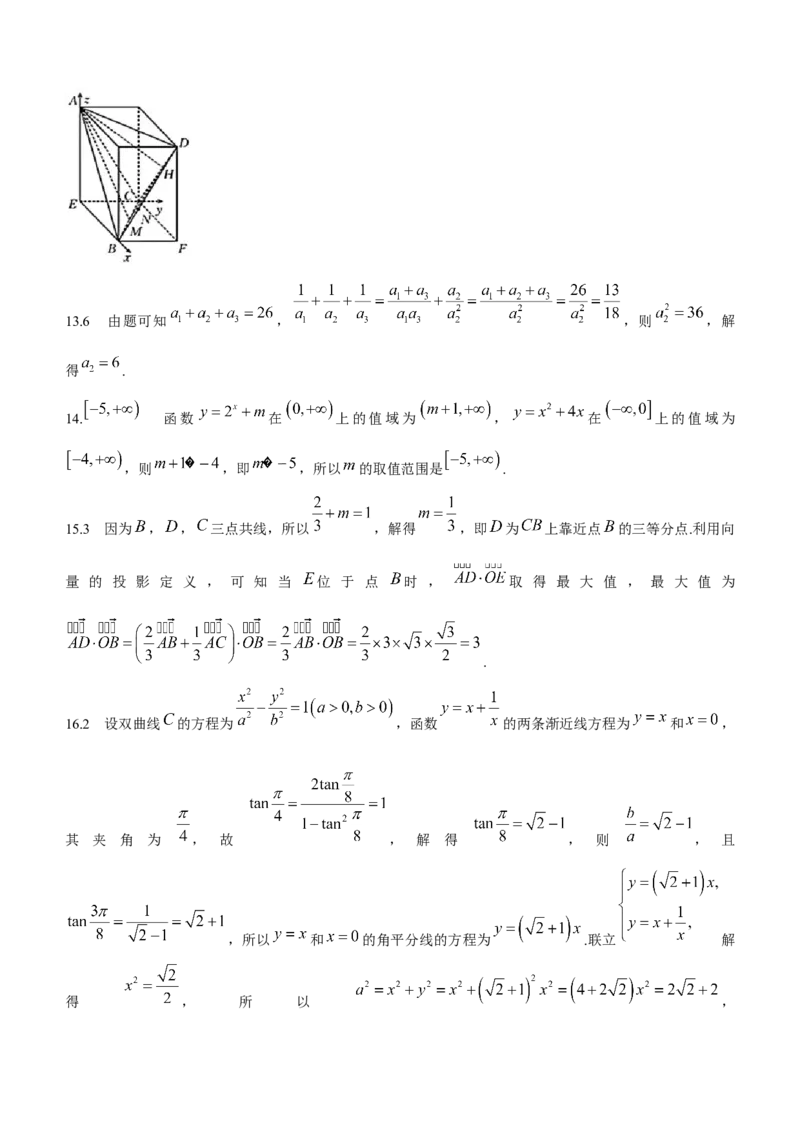
学科网(北京)股份有限公司13.6 由题可知 , ,则 ,解
得 .
14. 函数 在 上的值域为 , 在 上的值域为
,则 ,即 ,所以 的取值范围是 .
15.3 因为 , , 三点共线,所以 ,解得 ,即 为 上靠近点 的三等分点.利用向
量 的 投 影 定 义 , 可 知 当 位 于 点 时 , 取 得 最 大 值 , 最 大 值 为
.
16.2 设双曲线 的方程为 ,函数 的两条渐近线方程为 和 ,
其 夹 角 为 , 故 , 解 得 , 则 , 且
,所以 和 的角平分线的方程为 .联立 解
得 , 所 以 ,
学科网(北京)股份有限公司, 所 以 双 曲 线 的 方 程 为 , 故
.
17.解:(1)由 及正弦定理,
得 ,
则 ,即 ,
所以 的面积 .
(2)由余弦定理可知 .
因为 ,所以 ,当且仅当 时,等号成立.
设 为 边上的高,所以 ,即 ,
所以 边上的高的最大值为 .
18.(1)由题可知 ,
所以 ,
即 ,所以数列 是等差数列,
则
(2)
19.(1)证明:如图,连接 .
因为四边形 是边长为2的菱形, ,
所以 为等边三角形,则 .
学科网(北京)股份有限公司又平面 平面 ,平面 平面 ,
所以 平面 ,
因为 平面 ,所以 .
因为 , ,所以 .
因为 ,所以 平面 .
又 平面 ,所以 .
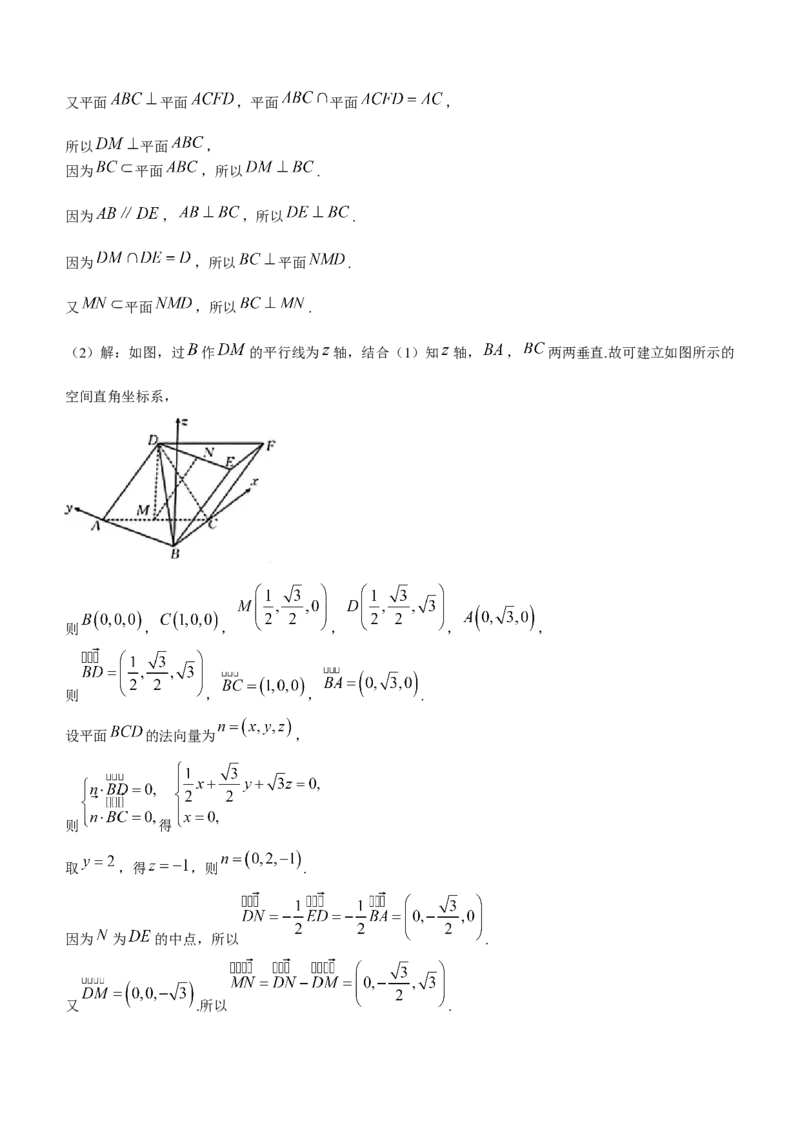
(2)解:如图,过 作 的平行线为 轴,结合(1)知 轴, , 两两垂直.故可建立如图所示的
空间直角坐标系,
则 , , , , ,
则 , , .
设平面 的法向量为 ,
则 得
取 ,得 ,则 .
因为 为 的中点,所以 .
又 .所以 .
学科网(北京)股份有限公司则 .
设直线 与平面 所成的角为 ,则 ,
即直线 与平面 所成角的正弦值为 .
20.解:(1)由题可知, 的取值可能为0,1,2.
,
,
,
则 的分布列为
0 1 2
.
(2)由题可知 ,当 时, 次底面的数字之和能被3整除的概率为 ,
所以 ,
则 ,所以数列 是以 为首项, 为公比的等比数列,
则 ,
即 .
学科网(北京)股份有限公司21.解:(1)由题意得 ,
化简得 ,即 .
故曲线 是焦点在 轴上的椭圆。
(2)设 , ,直线 的方程为 ,
则 ,
所以 , .
(也可以根据题目条件得出 , )
联立方程组 整理得 ,
则 ,所以 ,
所以线段 的中点为 ,
所以线段 的垂直平分线方程为 .
令 ,可得 ,即 .
因为 ,
由 ,可得 ,
学科网(北京)股份有限公司则 ,解得 ,
所以 的方程为 .
22.(1)解:由 且 ,可得 .
设 , ,则 ,
令 ,解得 .
当 时, , 单调递增;
当 时, , 单调递减.
又当 趋向于0时, 趋向于 ,当 趋向于 时, 趋向于0,
所以要使 的图象与直线 有两个交点,则 ,
故 的取值范围是 .
(2)证明: ,由(1)得 ,
则 , .
设 ,则 ,
即 ,
.
设 ,则 .
学科网(北京)股份有限公司设 ,则 ,
当 时, , 单调递减,
当 时, , 单调递增.
又 , , ,
所以存在唯一的 ,使得 ,
即 ,
所以 的最小值为 , ,
所以 ,故 .
学科网(北京)股份有限公司