文档内容
高二期中检测卷(二)
时间:120分钟 分值:150分
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合
题目要求的)
1.(2020·唐山市第十一中学高二期末)某公共汽车上有5名乘客,沿途有4个车站,乘客下车的可能方
式( )
A. 种 B. 种 C. 种 D. 种
【答案】D
【解析】每个乘客都有4种选法,共有 种,选D
2.(1-x)6展开式中,x的奇次项系数和为( )
A.32 B.-32
C.0 D.-64
【答案】B
【解析】 ,
所以x的奇次项系数和为 ,故选:B.
3.(2019·云南省云天化中学高二期中(理))为了解某社区居民的家庭年收入所年支出的关系,随机调
查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程 ,其中 , ,据此估计,该社区一户收入为16万
元家庭年支出为( )
A.11.80万元 B.12.56万元 C.11.04万元 D.12.26万元
【答案】B【解析】因为 , ,
所以 ,所以回归直线方程为 ,当 时, .
故选:B.
4.(2020·全国高二课时练习)若X~B(n,p),且E(X)=6,D(X)=3,则P(X=1)的值为( )
A.3×2-2 B.2-4 C.3×2-10 D.2-8
【答案】C
【解析】E(X)=np=6,D(X)=np(1-p)=3,∴p= ,n=12,则P(X=1)= ·( )1·( )11=3×2-10.
5.(2019·全国高二课时练习)从一批含有13件正品、2件次品的产品中,不放回地任取3件,则取出产品中
无次品的概率为( )
A.
B.
C.
D.
【答案】A
【解析】依题意可知,产品总数为 件,由超几何分布概率计算公式得取出产品中无次品的概率
为 ,故选A.
6.(2021·全国高二课时练习)已知某种药物对某种疾病的治愈率为 ,现有 位患有该病的患者服用了
这种药物, 位患者是否会被治愈是相互独立的,则恰有 位患者被治愈的概率为( )A. B. C. D.
【答案】B
【解析】由已知 位患者被治愈是相互独立的,每位患者被治愈的概率为 ,则不被治愈的概率为 所以
位患者中恰有1为患者被治愈的概率为 故选:B
7.(2021·长沙市·湖南师大附中高三月考)电视机的使用寿命与显像管开关的次数有关,某品牌的电视机
的显像管开关了 次还能继续使用的概率是 ,开关了 次后还能继续使用的概率是 ,则
已经开关了 次的电视机显像管还能继续使用到 次的概率是( )
A. B. C. D.
【答案】D
【解析】记事件 电视机的显像管开关了 次还能继续使用,记事件 电视机的显像管开关了
次后还能继续使用,则 , ,
所以,已经开关了 次的电视机显像管还能继续使用到 次的概率为
.故选:D.
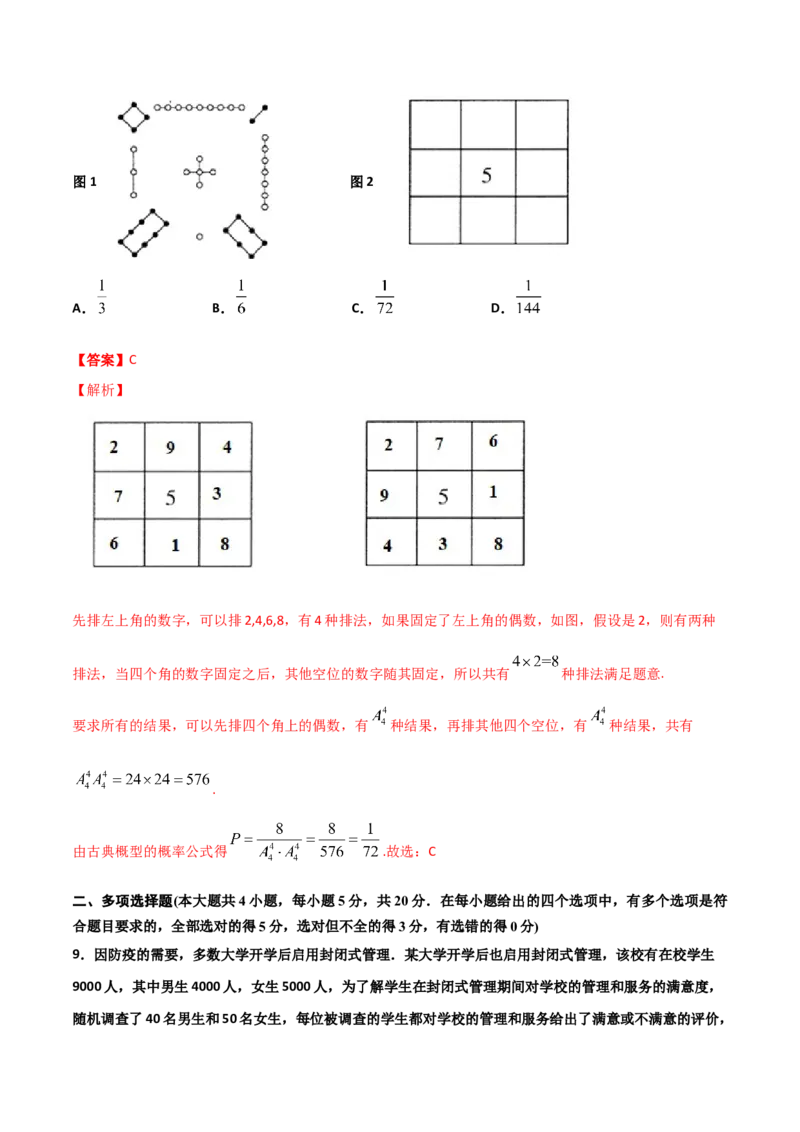
8.(2020·山东高三专题练习)洛书,古称龟书,是阴阳五行术数之源,被世界公认为组合数学的鼻祖,
它是中华民族对人类的伟大贡献之一.在古代传说中有神龟出于洛水,其甲壳上有图1:“以五居中,五
方白圈皆阳数,四隅黑点为阴数”,这就是最早的三阶幻方,按照上述说法,将1到9这九个数字,填在
如图2所示的九宫格里,九宫格的中间填5,四个角填偶数,其余位置填奇数.则每一横行、每一竖列以
及两条对角线上3个数字的和都等于15的概率是( )图1 图2
A. B. C. D.
【答案】C
【解析】
先排左上角的数字,可以排2,4,6,8,有4种排法,如果固定了左上角的偶数,如图,假设是2,则有两种
排法,当四个角的数字固定之后,其他空位的数字随其固定,所以共有 种排法满足题意.
要求所有的结果,可以先排四个角上的偶数,有 种结果,再排其他四个空位,有 种结果,共有
.
由古典概型的概率公式得 .故选:C
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符
合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分)
9.因防疫的需要,多数大学开学后启用封闭式管理.某大学开学后也启用封闭式管理,该校有在校学生
9000人,其中男生4000人,女生5000人,为了解学生在封闭式管理期间对学校的管理和服务的满意度,
随机调查了40名男生和50名女生,每位被调查的学生都对学校的管理和服务给出了满意或不满意的评价,经统计得到如下列联表:
满意 不满意
男 20 20
女 40 10
附表:
P
0.10 0.02 0.01
(K2≥k 0.05 0.001
0 5 0
)
2.70 3 5.02 6.63 10.82
k
6 .841 4 5 8
附:
以下说法正确的有( )
A.满意度的调查过程采用了分层抽样的抽样方法
B.该学校学生对学校的管理和服务满意的概率的估计值为0.6
C.有99%的把握认为学生对学校的管理和服务满意与否与性别有关系
D.没有99%的把握认为学生对学校的管理和服务满意与否与性别有关系
【答案】AC
【解析】因为男女比例为4000︰5000,故A正确.满意的频率为 ,所以该学校学生对
学校的管理和服务满意的概率的估计值约为0.667,所以B错误.
由列联表 ,故有99%的把握认为学生对学校的管理和服务满意与否
与性别有关系,所以C正确,D错误.故选:AC.
10.(2020·江苏高一期中)对于离散型随机变量 ,它的数学期望 和方差 ,下列说法正确
的是( )
A. 是反映随机变量的平均取值 B. 越小,说明 越集中于
C. D.
【答案】ABC【解析】离散型随机变量的期望反映了随机变量取值的平均水平,方差反映了随机变量取值偏离于均值的
平均程度,方差越小,说明随机变量的取值越集中于均值;即AB正确;由期望和方差的性质可得,
, ,即C正确,D错;故选:ABC.
11.(2020·江苏高二期中)设 ,则下列结论正确的是( )
A. B.
C. D.
【答案】ACD
【解析】因为 展开式的第 项为 ,
又 ,
所以 , ,则 ,故A正确;令 ,则
,
令 ,则 ;
令 ,则 ,
故 ,即B错;
,即C正确;
,即D正确;故选:
ACD.
12.(2020·江苏南京市·南京田家炳高级中学高三期中)下列命题中,正确的命题是( )
A.已知随机变量服从二项分布 ,若 , ,则B.已知 ,则
C.设随机变量 服从正态分布 ,若 ,则
D.某人在10次射击中,击中目标的次数为 , ,则当 时概率最大.
【答案】BCD
【解析】对于选项A:随机变量服从二项分布 , , ,可得 ,
,则 ,故选项A错误;
对于选项B:根据排列数和组合数的计算公式可得,
, ,
因为 ,所以有 ,即
解得 ,故选项B正确;
对于选项C:随机变量 服从正态分布 ,则图象关于 轴对称,若 ,则
,即 ,故选项C正确;
对于选项D:因为在10次射击中,击中目标的次数为 , ,
当 时,对应的概率 ,
所以当 时, ,由 得 ,即 ,
因为 ,所以 且 ,
即 时,概率 最大,故选项D正确.故选:BCD.
第Ⅱ卷(非选择题,共90分)
三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.(2020·全国高二单元测试)若 ,则 ________.
【答案】
【解析】由 可得: ,
即 ,解得 .故答案为:
14.(2021·黑龙江大庆市·高三一模(理))为了研究某班学生的脚长 (单位:厘米)和身高 (单位:厘
米)的关系,从该班随机抽取 名学生,根据测量数据的散点图可以看出 与 之间有线性相关关系,设
其回归直线方程为 .已知这组数据的样本中心点为 , ,若该班某学生的脚长为
厘米,据此估计其身高为________厘米.
【答案】
【解析】根据题意,计算 , , ;
∴ ,
∴ ,
当 时,计算 ,
据此估计其身高为 (厘米).故答案为:15.(2020·江西南昌市·南昌二中高三其他模拟(理))一台仪器每启动一次都随机地出现一个5位的二
进制数 ,其中 的各位数字中, , ,3,4, 出现0的概率为 ,
出现1的概率为 ,则启动一次出现的数字 中恰有两个0的概率为__.
【答案】
【解析】根据题意, 中恰有两个0的概率,即在 、 、 、 四个数中恰好有2个0,2个1,则
中恰有两个0的概率 ;故答案为: .
16.(2020·天津北辰区·高三二模)近年来,空气质量成为人们越来越关注的话题,空气质量指数(Air
Quality Index,简称AQI)是定量描述空气质量状况的指数.环保部门记录了某地区7天的空气质量指数,
其中,有4天空气质量为优,有2天空气质量为良,有1天空气质量为轻度污染.现工作人员从这7天中
随机抽取3天进行某项研究,则抽取的3天中至少有一天空气质量为良的概率为________;记 表示抽取
的3天中空气质量为优的天数,则随机变量 的数学期望为________.
【答案】
【解析】设事件A表示“抽取3天中至少有一天空气质量为良”,
事件B表示“抽取的3天空气质量都不为良”,
则事件A与事件B互为对立事件,
所以 ;
随机变量 的可能取值为 ,概率为 ,
所以随机变量 分布列为:随机变量 的数学期望为
故答案为: ;
四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(2020·全国高二课时练习)在①只有第八项的二项式系数最大,②奇数项二项式系数之和为 ,③
各项系数之和为 ,这三个条件中任选一个,补充在下面问题中,若问题中的 存在,求 的值;若 不
存在,说明理由.
设二项式 ,若其展开式中,______,是否存在整数 ,使得 是展开式中的常数项?
注:如果选择多个条件分别解答,按第一个解答给分.
【解析】若选填条件①,即只有第八项的二项式系数最大,即 最大,由二项式系数的性质可得,
;
若选填条件③,即各项系数之和为 ,则 ,即 ;
二项式 展开式的通项: .
由 ,得 .
即存在整数 ,使得 是展开式中的常数项;
若选填条件②,即奇数项二项式系数之和为 ,
则 ,∴ .二项式 展开式的通项: .
由 ,得 .
即不存在整数k,使得 是展开式中的常数项.
18.(2020·全国高二课时练习)在学校组织的足球比赛中,某班要与其他4个班级各赛一场,在这四场比
赛的任意一场中,此班级每次胜、负、平的概率都相等.已知这四场比赛结束后,该班胜场多于负场.
(1)求该班胜场多于负场的所有可能情况的种数;
(2)若胜场次数为 ,求 的分布列.
【解析】(1)若胜一场,则其余为平,共有 种情况;
若胜两场,则其余两场为一负一平或两平,共有 种情况;
若胜三场,则其余一场为负或平,共有 种情况;
若胜四场,则只有1种情况.
综上,共有 种情况.
(2) 的可能取值为1,2,3,4,
由(1)可得: , , ,
所以 的分布列为:
1 2 3 4
19.(2020·全国高二单元测试)有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台
加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的
25%,30%,45%.
(1)任取一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
【解析】设B=“任取一个零件为次品”,A=“零件为第i台车床加工”(i=1,2,3),则Ω=
iA ∪A ∪A ,A ,A ,A 两两互斥.根据题意得
1 2 3 1 2 3
P(A )=0.25,P(A )=0.3,P(A )=0.45,
1 2 3
P(B|A )=0.06,P(B|A )=P(B|A )=0.05.
1 2 3
(1)由全概率公式,得
P(B)=P(A )P(B|A )+P(A )P(B|A )+P(A )P(B|A )
1 1 2 2 3 3
=0.25×0.06+0.3×0.05+0.45×0.05
=0.0525.
(2)“如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率”,就是计算在B发生的条件
下,事件A发生的概率.
i
P(A |B)= =
1
= = .
类似地,可得
P(A |B)= ,P(A |B)= .
2 3
20.(2020·四川高二期末(理))甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为
与 ,且乙投球2次均未命中的概率为 .
(Ⅰ)求乙投球的命中率 ;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为 ,求 的分布列和数学期望.
【解析】(I)设“甲投球一次命中”为事件 ,“乙投球一次命中”为事件 .
由题意得 解得 或 (舍去),所以乙投球的命中率为 .
(II)由题设知(I)知 , , , ,可能取值为
故 ,
,
的分布列为
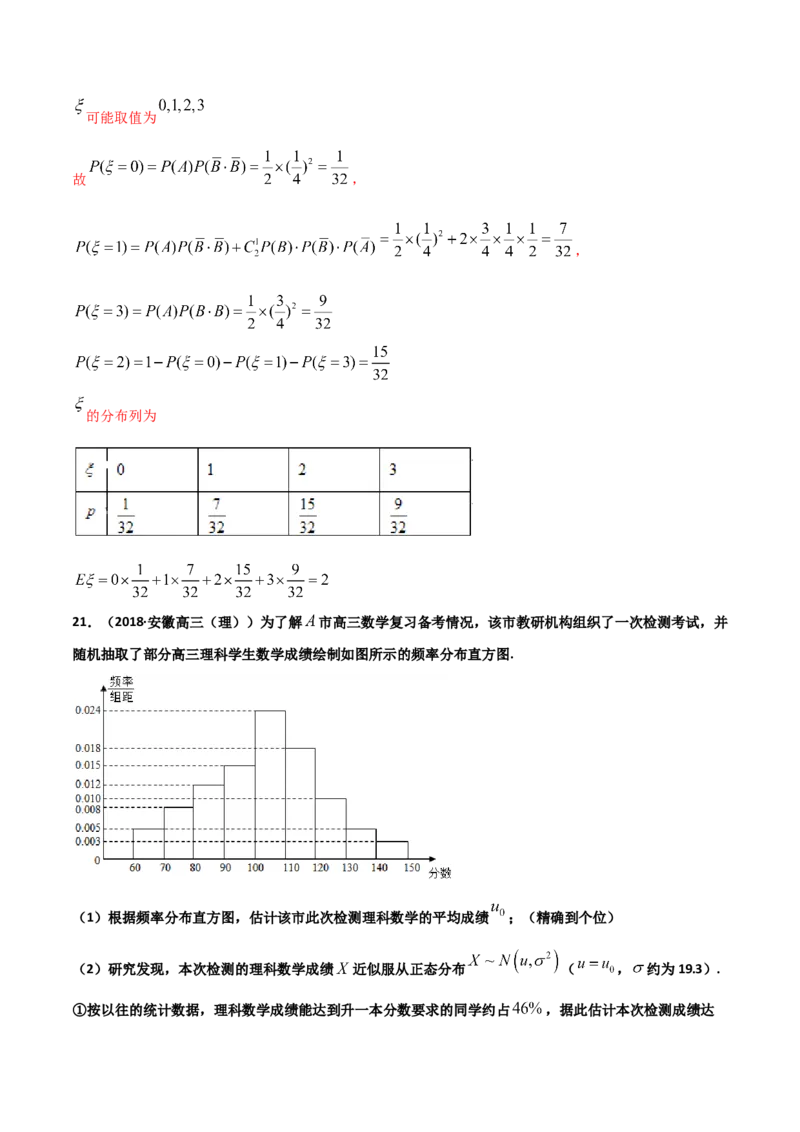
21.(2018·安徽高三(理))为了解 市高三数学复习备考情况,该市教研机构组织了一次检测考试,并
随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.
(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩 ;(精确到个位)
(2)研究发现,本次检测的理科数学成绩 近似服从正态分布 ( , 约为19.3).
①按以往的统计数据,理科数学成绩能达到升一本分数要求的同学约占 ,据此估计本次检测成绩达到升一本的理科数学成绩大约是多少分?(精确到个位)
②已知 市理科考生约有10000名,某理科学生此次检测数学成绩为107分,则该学生全市排名大约是多
少名?
(说明: 表示 的概率, 用来将非标准正态分布化为标准正态
分布,即 ,从而利用标准正态分布表 ,求 时的概率 ,这里
,相应于 的值 是指总体取值小于 的概率,即 .参考数据:
, , ).
【解析】(1)该市此次检测理科数学成绩平均成绩约为:
(分).
(2)①记本次考试成绩达到升一本的理科数学成绩约为 ,
根据题意, ,
即 .
由 ,得
解得 ,
所以本次考试成绩达到升一本的理科数学成绩约为117分.
② ,所以理科数学成绩为107分时,大约排在 名.
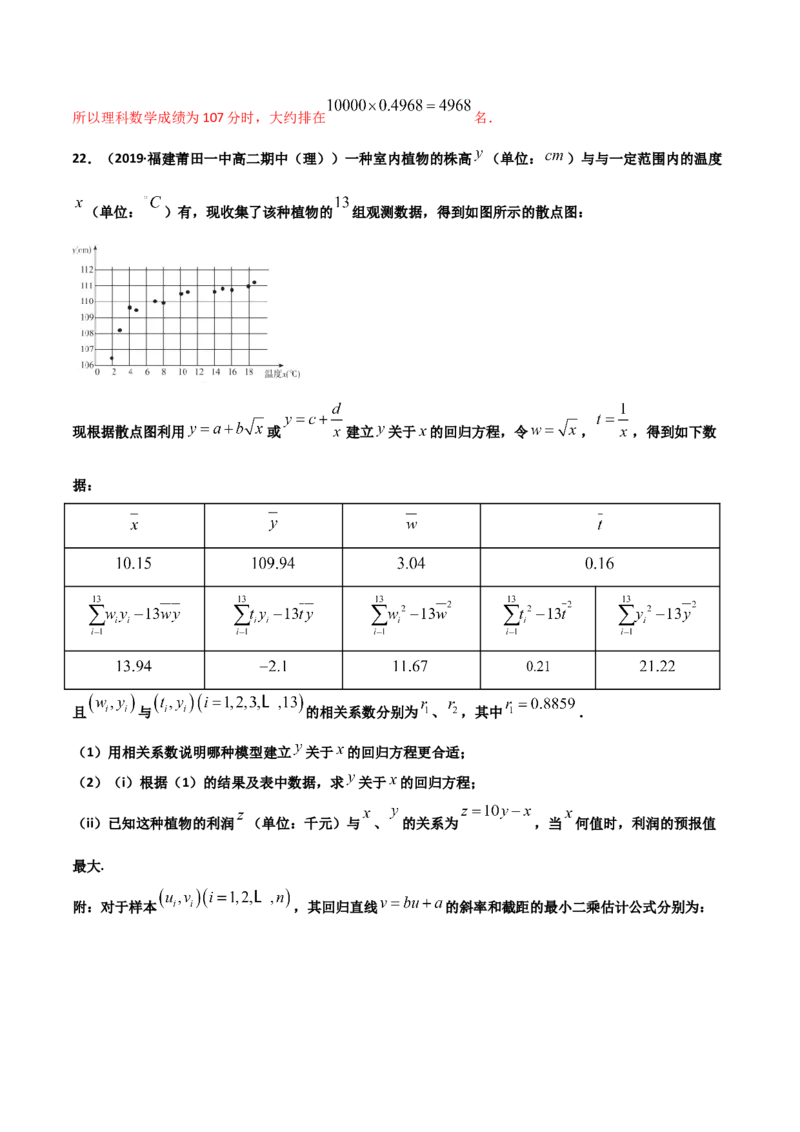
22.(2019·福建莆田一中高二期中(理))一种室内植物的株高 (单位: )与与一定范围内的温度
(单位: )有,现收集了该种植物的 组观测数据,得到如图所示的散点图:
现根据散点图利用 或 建立 关于 的回归方程,令 , ,得到如下数
据:
且 与 的相关系数分别为 、 ,其中 .
(1)用相关系数说明哪种模型建立 关于 的回归方程更合适;
(2)(i)根据(1)的结果及表中数据,求 关于 的回归方程;
(ii)已知这种植物的利润 (单位:千元)与 、 的关系为 ,当 何值时,利润的预报值
最大.
附:对于样本 ,其回归直线 的斜率和截距的最小二乘估计公式分别为:, ,
相关系数 , .
【解析】(1)由相关系数公式可得
,
,所以用 模型建立 与 的回归方程更合适;
(2)(i)由题意可得 ,
,
因此, 关于 的回归方程为 ;
(ii)由题意知 ,
由基本不等式可得 ,所以 ,
当且仅当 时等号成立,
所以当温度为 时,这种草药的利润 的预报值最大.