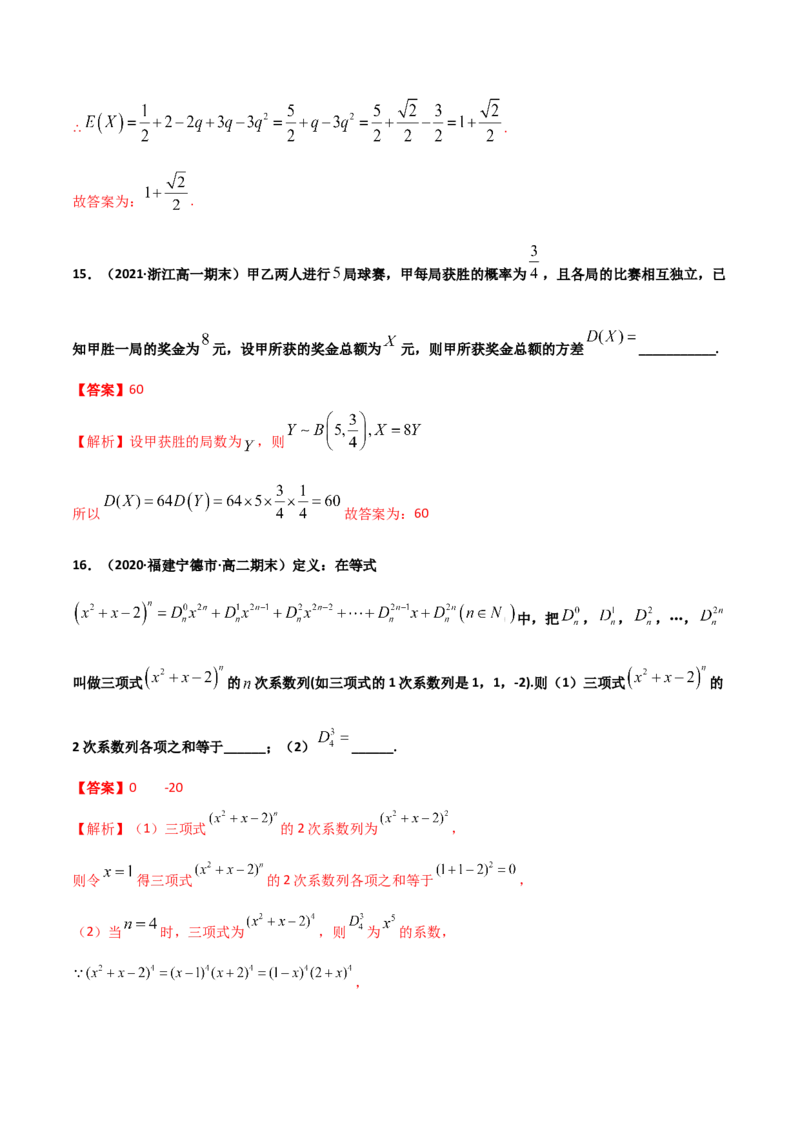文档内容
高二期中检测卷(三)
时间:120分钟 分值:150分
注意事项:
本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合
题目要求的)
1.(2021·江西赣州市·高二期末(文))小明研究变量x与y的线性相关性,用线性回归方法求出了直线
,小亮研究变量ν与w的线性相关性,用线性回归方法求出了直线 ,两个人发现平均值 ,
则下列说法一定不正确的是( )
A. 与 重合 B. 与 平行 C. 与 相交 D. 与 垂直
【答案】B
【解析】由线性回归直线的概念可知,直线 过其样本中心点 ,直线 过其样本中心点 ,而
,故两条直线有公共点 .
当 与 重合、相交或垂直时都有公共点,可能正确;当 与 平行时,没有公共点,故一定不正确.故选:
B.
2.(2021·河南驻马店市·高三期末(理))已知 ,且 ,则 ( )
A. B. C. D.
【答案】D
【解析】因为 服从二项分布 ,所以 ,得 ,故
.故选:D.
3.(2021·辽宁高三月考)唐代诗人张若虚在《春江花月夜》中曾写道:“春江潮水连海平,海上明月共
潮生.”潮水的涨落和月亮的公转运行有直接的关系,这是一种自然现象.根据历史数据,已知沿海某地在某个季节中每天出现大潮的概率均为 ,则该地在该季节内连续三天内,至少有两天出现大潮的概率为
( )
A. B. C. D.
【答案】A
【解析】该地在该季节内连续三天内,至少有两天出现大潮包括两天或三天出现大潮,
有两天出现大潮概率为 ,
有三天出现大潮概率为 ,
所以至少有两天出现大潮的概率为 ,故选:A.
4.(2021·全国高二课时练习)2020年是全面建成小康社会的目标实现之年,也是全面打赢脱贫攻坚战的
收官之年.为更好地将“精准扶贫”落到实处,某地安排7名干部(3男4女)到三个贫困村调研走访,每个村
安排男、女干部各1名,剩下1名干部负责统筹协调,则不同的安排方案有( )
A.72种 B.108种 C.144种 D.210种
【答案】C
【解析】∵每个村男、女干部各1名,∴可先安排男干部,共 种,再安排女干部,共有
种,∴共有 种不同的安排方案故选:C.
5.(2021·广西玉林市·高三其他模拟(理)) 的展开式中, 的系数是( )
A. B. C. D.
【答案】C
【解析】 展开式通项公式为: ,令 ,解得: , 的系数为 .故选:C.
6.(2021·全国高三其他模拟)甲、乙两人进行围棋比赛,若其中一人连续赢两局,则比赛结束.已知每局
比赛结果相互独立,且每局甲胜的概率为0.6(没有平局),若比赛在第三局结束,则甲获胜的概率为
( )
A.0.6 B.0.4 C.0.36 D.0.144
【答案】A
【解析】“比赛在第三局结束”记为事件 ,“甲获胜”记为事件 ,
则 .故选:A
7.(2019·广东佛山实验中学高三月考(理))如图,一只蚂蚁从点 出发沿着水平面的线条爬行到点 ,
再由点 沿着置于水平面的正方体的棱爬行至顶点 ,则它可以爬行的不同的最短路径有( )条
A.40 B.60 C.80 D.120
【答案】B
【解析】蚂蚁从 到 需要走五段路,其中三纵二竖,共有 条路径,从 到 共有 条路
径,根据分步计数乘法原理可知,蚂蚁从 到 可以爬行的不同的最短路径有 条,故选B.
8.(2020·安徽高二月考(文))2020年6月9日,安徽省教育厅宣布,为应对7月高考、中考期间高温
天气,给学生创造舒适考场环境,全部地市将在中考、高考考场安装空调.某商场销售某种品牌的空调器,
每周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器
需交保管费100元;若供不应求,则可从其他商店调剂供应,此时调剂的每台空调器仅获利润200元.该
商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n 18 19 20 21 22频数 1 2 3 3 1
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利
润(单位:元).则当周的平均利润为( )
A.10000元 B.9400元
C.8800元 D.9860元
【答案】D
【解析】当 时, ,
当 时, ,
则可知 的可能取值为8800,9400,10000,10200,10400,
, , , ,
,
(元).
故选:D.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符
合题目要求的,全部选对的得5分,选对但不全的得3分,有选错的得0分)
9.(2021·湖北黄冈市·高二期末)下列命题中正确的有( )
A.对立事件一定是互斥事件,但互斥事件不一定是对立事件
B.两个随机变量的线性相关系数越大,则两个变量的线性相关性越强
C.回归直线 必过样本点的中心
D.相关指数 越大,则模型的拟合效果越好
【答案】ACD
【解析】对于A:互斥事件不一定是对立事件,对立事件一定是互斥事件,所以A正确;
对于B:两个随机变量的线性相关系数的绝对值越大(越接近1),则两个变量的线性相关性越强,故B错
误;对于C:回归直线 必过样本点的中心,故C正确;
对于D:在线性回归模型中,相关指数 越接近于1,则模型回归效果越好,故D正确;故选:ACD
10.下列关于排列数与组合数的等式中,正确的是( )
A. B.
C. D.
【答案】ABD
【解析】对于A, ,故A正确;
对于B, , ,
所以
所以 ,故B正确;
对于C, ,故C错误;
对于D, ,故D正确;故
选:ABD
11.(2021·全国高二课时练习)对于 展开式的二项式系数下列结论正确的是( )
A. B.
C.当 为偶数时, D.
【答案】ABC【解析】对于A,由组合数的运算直接可得 ,故A正确;
对于B,由杨辉三角直接可得 ,故B正确;
对于C,二项式展开式中,令 ,不论 为奇数还是偶数,都可得 ,故
C正确;
对于D,由选项C可知 ,故D错误.故选:ABC
12.(2021·湖北黄冈市·高二期末)为弘扬我国古代“六艺”文化,某研学旅行夏令营主办单位计划在暑
假开设“礼、乐、射、御、书、数”六门体验课程,若甲乙丙三名同学各只能体验其中一门课程.则(
)
A.甲乙丙三人选择课程方案有 种方法
B.恰有三门课程没有被三名同学选中的概率为
C.已知甲不选择课程“御”的条件下,乙丙也不选择“御”的概率为
D.设三名同学选择课程“礼”的人数为 ,则
【答案】BCD
【解析】甲乙丙三名同学各只能体验其中一门课程,则选择方法有 种,故A错误;恰有三门课程
没有被三名同学选中,表示三位同学每个人选择了不重复的一门课程,所以概率为 ,故B
正确;已知甲不选择课程“御”的概率为 ,甲乙丙都不选择“御”的概率为 ,所以条件概率为 ,故C正确;三名同学选择课程“礼”的人数为 ,则 服从二项分布 ,则
,故D正确.故选:BCD.
第Ⅱ卷(非选择题,共90分)
三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.(2021·山东滨州市·高三一模)某公司对近5年的年广告支出 (单位:万元)与年利润 (单位:万
元)进行了初步统计,如下表所示:
年广告支出 1 2 3 4 5
年利润 5 6 8 10
由上表中数据求得年广告支出 与年利润 满足线性回归方程 ,则 的值为______.
【答案】7
【解析】由已知, , ,
所以 ,解得 .故答案为:7.
14.(2021·聊城市·山东聊城一中高三一模)设X是一个离散型随机变量,其分布列为:
X 1 2 3
P
则X的数学期望为_________.
【答案】
【解析】由 得, ,∴ .
故答案为: .
15.(2021·浙江高一期末)甲乙两人进行 局球赛,甲每局获胜的概率为 ,且各局的比赛相互独立,已
知甲胜一局的奖金为 元,设甲所获的奖金总额为 元,则甲所获奖金总额的方差 ___________.
【答案】60
【解析】设甲获胜的局数为 ,则
所以 故答案为:60
16.(2020·福建宁德市·高二期末)定义:在等式
中,把 , , ,…,
叫做三项式 的 次系数列(如三项式的1次系数列是1,1,-2).则(1)三项式 的
2次系数列各项之和等于______;(2) ______.
【答案】0 -20
【解析】(1)三项式 的2次系数列为 ,
则令 得三项式 的2次系数列各项之和等于 ,
(2)当 时,三项式为 ,则 为 的系数,
,的通项公式为 , 的通项公式为 ,
的系数为 .
即
故答案为: ; ;
四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.已知(1+2x-x2)7=a +a x+a x2+…+a x13+a x14.
0 1 2 13 14
(1)求a +a +a +…+a ;
0 1 2 14
(2)求a +a +a +…+a .
1 3 5 13
【解析】(1)令x=1,则a +a +a +…+a =27=128.
0 1 2 14
(2)令x=-1,则a -a +a -a +…-a +a =(-2)7=-128.
0 1 2 3 13 14
结合(1)得:2(a +a +…+a )=256,
1 3 13
∴a +a +a +…+a =128.
1 3 5 13
18.玻璃杯成箱出售,每箱20只,假设各箱含0,1,2只残次品的概率分别为0.8,0.1,0.1,一顾客欲购一箱玻
璃杯,售货员随意取一箱,顾客开箱随意地察看四只,若无残次品,则买下该箱,否则退回.试求:
(1)顾客买下该箱的概率α;
(2)在顾客买下的一箱中,求无残次品的概率β.
【解析】设A=‘顾客买下该箱’,
B=‘箱中恰有i件残次品’,i=0,1,2,
(1)α=P(A)=P(B )P(A|B )+P(B )P(A|B )+P(B )P(A|B )=0.8+0.1× +0.1× ≈0.94.
0 0 1 1 2 2
(2)β=P(B |A)= ≈0.85.
0
19.(2020·防城港市防城中学高二期中(理))“每天锻炼一小时,健康工作五十年,幸福生活一辈
子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到
了如下列联表:
男性 女性 合计
爱好 10不爱好 8
合计 30
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是 .
(1)请将上面的列联表补充完整,并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为X,求X的分布列、数
学期望.
【解析】(1)由30人中随机抽取1人抽到爱好运动的员工的概率是 ,
故爱好运动的员工共有16人,由表中男爱好运动的员工为10人,
可得女爱好运动的员工有6人,
故列联表补充如下:
男性 女性 合计
爱好 10 6 16
不爱好 6 8 14
合计 16 14 30
由已知数据可求得:
,
所以没有把握认为爱好运动与性别有关;
(2)X的可能取值为0,1,2.
, ,
,
所以X的分布列为:
X 0 1 2P
X的数学期望为:
.
20.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η,且ξ,η的分布列为:
ξ 1 2 3
P a 0.1 0.6
η 1 2 3
P 0.3 b 0.3
(1)求a,b的值;
(2)计算ξ,η的期望与方差,并以此分析甲、乙技术状况.
【解析】(1)由离散型随机变量的分布列的性质可知
a+0.1+0.6=1,
∴a=0.3.
同理0.3+b+0.3=1,b=0.4.
(2)E(ξ)=1×0.3+2×0.1+3×0.6=2.3,
E(η)=1×0.3+2×0.4+3×0.3=2,
D(ξ)=(1-2.3)2×0.3+(2-2.3)2×0.1+(3-2.3)2×0.6=0.81,
D(η)=(1-2)2×0.3+(2-2)2×0.4+(3-2)2×0.3=0.6.
由于E(ξ)>E(η),说明在一次射击中,甲的平均得分比乙高,但D(ξ)>D(η),说明甲得分的稳定性不如乙,因
此甲、乙两人技术水平都不够全面,各有优势与劣势.
21.(2020·四川高三期末(文))习近平总书记在党的十九大报告中指出,要在“幼有所育、学有所教、
劳有所得、病有所医、老有所养、住有所居、弱有所扶”上不断取得新进展,保证全体人民在共建共享发
展中有更多获得感.现S市政府针对全市10所由市财政投资建设的敬老院进行了满意度测评,得到数据如
下表:
敬老院 A B C D E F G H I K
满意度x(%) 20 34 25 19 26 20 19 24 19 13投资原y(万元) 80 89 89 78 75 71 65 62 60 52
(1)求投资额 关于满意度 的相关系数;
(2)我们约定:投资额 关于满意度 的相关系数 的绝对值在0.75以上(含0.75)是线性相关性较强,
否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即满意度最低的敬老院市财
政不再继续投资,改为区财政投资).求在剔除“末位淘汰”的敬老院后投资额 关于满意度 的线性回归
方程(系数精确到0.1)
参考数据: , , ,
, .
附:对于一组数据 ,其回归直线 的斜率和截距的最小二乘估计公
式分别为: .线性相关系数 .
【解析】(1)由题意,根据相关系数的公式,可得
.
(2)由(1)可知,因为 ,所以投资额 关于满意度 没有达到较强线性相关,
所以要“末位淘汰”掉K敬老院.
重新计算得 , ,,
,
所以 ,
.
所以所求线性回归方程为 .
22.某工厂生产某种零件,检验员每天从该零件的生产线上随机抽取16个零件,并测量其尺寸(单位:
cm).根据长期生产经验,可以认为这条生产线在正常状态下生产的零件服从正态分布N(μ,σ2).
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求
P(X≥1)及X的数学期望;
(2)下面是检验员在一天内抽取的16个零件的尺寸:
10.12 9.97 10.01 9.95 10.02 9.98 9.21 10.03
10.04 9.99 9.98 9.97 10.01 9.97 10.03 10.11
经计算得 , ,其中x为抽取的第i
i
个零件的尺寸,i=1,2,…,16.用样本平均数 作为μ的估计值 ,用样本标准差s作为σ的估计值 ,
利用估计值判断是否对当天的生产过程进行检查?剔除(μ-3σ,μ+3σ)之外的数据,用剩下的数据估计μ
和σ(精确到0.01).
参考数据:若随机变量X服从正态分布N(μ,σ2),则P(μ-3σ<x<μ+3σ)=0.997 4,0.997416≈0.9592,
【解析】(1)∵抽取的一个零件尺寸在(μ-3σ,μ+3σ)内的概率为0.997 4,
∴零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.002 6,
故X~B(16,0.0026).P(X≥1)=1-P(X=0)=1-0.997416≈0.0408;
X的数学期望为E(X)=16×0.0026=0.0416.
(2) ,s≈0.20,得 , .
∵样本数据可以看到有一个零件的尺寸在 之外,
∴需要对当天的生产过程进行检查.
剔除(μ-3σ,μ+3σ)之外的数据9.21之后,
剩下数据的平均数 ,可得μ的估计值为10.01.
∵ ,
剔除 之外的数据9.21之后,
剩下数据的方差为 ,
∴σ的估计值为 .