数学答案（宁波十校3月联考）_2024年3月_013月合集_2024届浙江省宁波“十校”高三3月联考_宁波“十校”2024届高三3月联考数学

宁波“十校”2024 届高三 3 月联考 数学参考答案 一、选择题（本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项符合 题目要求） 1 2 3 4 5 6 7 8 D C D B B C A D 二、选择题（本大题共3小题，每小题6分，共18分. 在每小题给出的四个选项中，有多个选项符 合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.） 9 10 11 BCD ABD ABC 三、填空题（本大题共3小题，每小题5分，共15分.） 12． 宁波“十校” 数学参考答案 第 1 页 共 6 页 7 2 5 13．16 14． 1 3 0 四、解答题（本大题共5小题，共77分. 解答应写出必要的文字说明，证明过程或演算步骤.） 15．（本题共13分）解： （1）由题意： ( s in A c o s B − c o s A s in B ) c o s C = c o s B  ( s in A c o s C − c o s A s in C ) ，------------2分 整理得cosA(cosBsinC−sinBcosC)=cosAsin(C−B)=0， 故cosA=0或 s in ( C − B ) = 0 ， 当cosA=0时， A = π 2 ， ABC为直角三角形，----------------------------------------------3分 当 s in ( C − B ) = 0 时， B = C ， A B C 为等腰三角形．---------------------------------------5分 （2）由正弦定理 s a in A = s b in B 得 a s in B = b s in A = 1 ，-------------------------------------------7分 ∴ a = s 1 in B , ∴ 2 a 2 + 1 2 b + 1 2 c = 2 s in 2 B + s in A -----------------------------------------------9分 又B=C,A+B+C=π， 2 s in 2 B s in A 1 c o s 2 B s in 2 B 1 2 s in ( 2 B 4 )   + = − + = + − ，---------------------------11分 因为 A B C 为锐角三角形，所以  0 0   B A  = π 2 π − 2 B  π 2 ，解得 π 4  B  π 2 ，   3 ∴当2B− = 时，即B= 时取最大值，最大值为 4 2 8 2 + 1 . 综上，最大值为 2+1.----------------------------------------------------------------------------13分 16．（本题共15分）解： （1）证明：由四边形ABCD是直角梯形，AB= 3，BC=2AD=2，AB⊥BC，可得DC=2，∠BCD= 宁波“十校” 数学参考答案 第 2 页 共 6 页 3  ，从而△BCD是等边三角形，BD=2，BD平分∠ADC. ∵E为CD的中点，∴DE=AD=1，∴BD⊥AE，-----------------------------------3分 又∵PB⊥AE，PB∩BD=B，∴AE⊥平面PBD. 又∵AE⊂平面ABCD ∴平面PBD⊥平面ABCD.----------------------------------------------6分 （2）在平面PBD内作PO⊥BD于O，连接OC，又∵平面PBD⊥平面ABCD，平面PBD∩平面 ABCD=BD， ∴PO⊥平面ABCD，∴∠PCO为PC与平面ABCD所成的角，则∠PCO= 3  ∴易得OP=3.-----------------------------------------------------------------------------------------8分 又OC= 3，PB=PD，PO⊥BD，所以O为BD的中点，OC⊥BD. 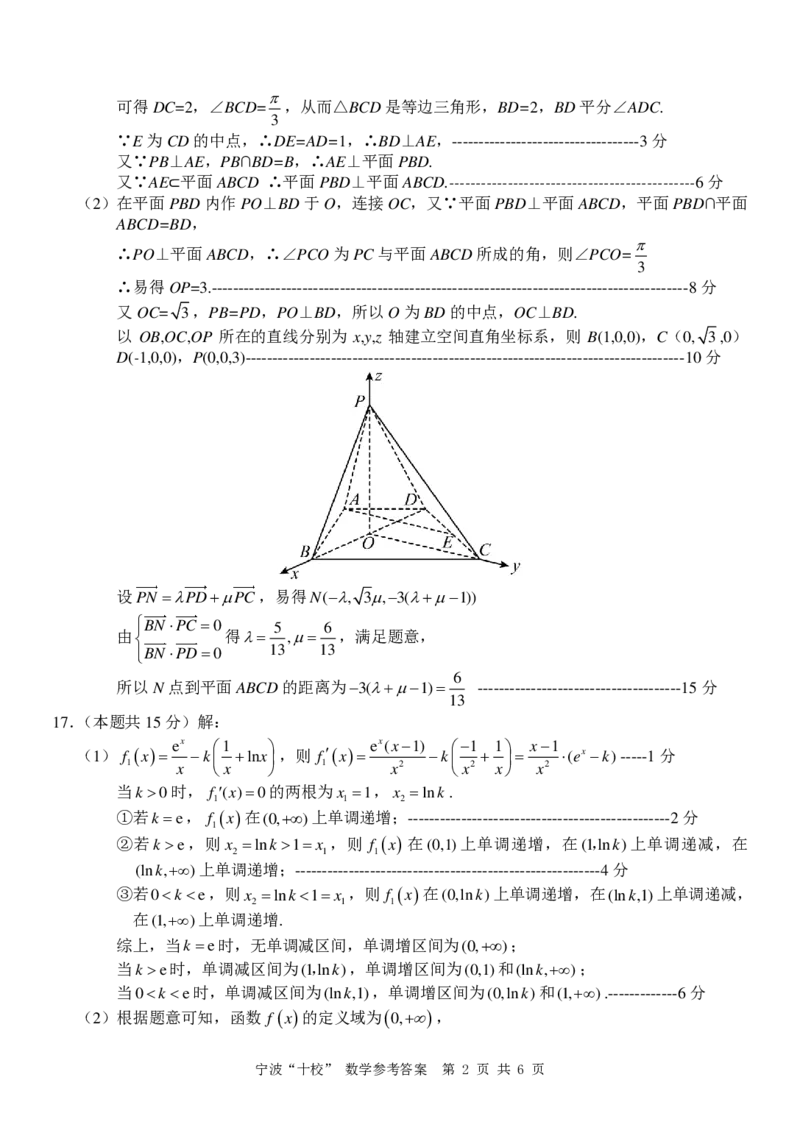以 OB,OC,OP 所在的直线分别为 x,y,z 轴建立空间直角坐标系，则 B(1,0,0)，C（0, 3,0） D(-1,0,0)，P(0,0,3)----------------------------------------------------------------------------------10分 设 P N P D P C   = + ，易得N(−, 3,−3(+−1)) 由  B B N N   P P C D = = 0 0 得 5 1 3 , 6 1 3   = = ，满足题意， 6 所以N点到平面ABCD的距离为−3(+−1)= --------------------------------------15分 13 17．（本题共15分）解： （1） f1 ( x ) = x e x − k  1 x + ln x  ，则  f1 ( x ) = e x ( x x − 2 1 ) − k  − x 1 2 + 1 x  = x − 2 x 1  ( e x − k ) -----1分 当 k  0 时， f1 ( x ) = 0 的两根为 x 1 = 1 ， x 2 = ln k . ①若 k = e ， f (x)在 1 ( 0 , +  ) 上单调递增；-------------------------------------------------2分 ②若k e，则x =lnk1=x ，则 2 1 f1 ( x ) 在(0,1)上单调递增，在(1，lnk)上单调递减，在 ( ln k , +  ) 上单调递增；---------------------------------------------------------4分 ③若 0  k  e ，则 x 2 = ln k  1 = x 1 ，则 f (x)在 1 ( 0 , ln k ) 上单调递增，在(lnk,1)上单调递减， 在 (1 , +  ) 上单调递增. 综上，当 k = e 时，无单调减区间，单调增区间为(0,+)； 当k e时，单调减区间为(1，lnk)，单调增区间为(0,1)和(lnk,+)； 当0ke时，单调减区间为(lnk,1)，单调增区间为(0,lnk)和(1,+).-------------6分 （2）根据题意可知，函数 f (x)的定义域为(0,+)，则 宁波“十校” 数学参考答案 第 3 页 共 6 页 f  ( x ) = e x  x 3 − x e 6 x  3 x 2 − k  − 3 x 2 + 1 x  = ( x − 3 )  e x − x k 4 x 2 ， 由函数 f ( x ) 有三个极值点 x 1 , x 2 , x 3 可知 f  ( x ) = ( x − 3 )  e x − x k 4 x 2 = 0 在 ( 0 , )  + 上至少有三个 实数根；显然 f  ( 3 ) = 0 ，则需方程 e x − x k 4 x 2 = 0 ， 也即 e x − k x 2 = 0 有两个不等于3的不相等的实数根；--------------------------------------8分 由 e x − k x 2 = 0 ex 可得k = ，x(0,+)， x2 令 g ( x ) = e x x 2 , x  ( 0 , +  ) ，则 g  ( x ) = e x ( x x − 3 2 ) , x  ( 0 , +  ) ，-----------------------------10分 显然当 x  ( 0 , 2 ) 时， g  ( x )  0 ，即 g ( x ) 在 ( 0 , 2 ) 上单调递减； 当 x  ( 2 , +  ) 时， g  ( x )  0 ，即 g ( x ) 在 ( 2 , +  ) 上单调递增； 所以 g ( x )  g ( 2 ) = 2 e 4 ，----------------------------------------------------------------------------12分 画出函数 g ( x ) = e x x 2 , x  ( 0 , +  ) 与函数 y = k 在同一坐标系下的图象， 由图可得 k  2 e 4 且 k  e 9 3 时， k = e x x 2 在 ( 0 , )  + 上有两个不等于3的相异的实数根， 经检验可知当 k   2 e 4 , e 9 3    e 9 3 , +   时，导函数 f  ( x ) = ( x − 3 )  e x − x k 4 x 2 = 0 在 x 1 , x 2 , x 3 左右 符号不同，即 x 1 , x 2 , x 3 均是 f  ( x ) = 0 的变号零点，满足题意； 因此实数 k 的取值范围是 k   2 e 4 , 3 e 9    3 e 9 , +   -------------------------------------------15分 （注：未去掉 3 e 9 ，扣1分） 18．（本题共17分）解： （1）依题意， X ~ B  5 , 1 2  ， 1 5 1 则P(X =0)=  = ， 2 32 P ( X = 1 ) = C 15  1 2  4  1 2  = 5 3 2 ， 1 3 1 2 10 5 1 2 1 3 5 P(X =2)=C2     = = ，P(X =3)=C3     = 5 2 2 32 16 5 2 2 16 P ( X = 4 ) = C 45  1 2   1 2  4 = 5 3 2 1 5 1 ，P(X =5)=  = ， 2 32 故 X 的分布列为： X 0 1 2 3 4 5 1 5 5 5 5 1 P 32 32 16 16 32 32----------------------------------------------5分 1 5 故E(X)=5 = ．-----------------------------------------------------------------7分 2 2 （2）事件“ 宁波“十校” 数学参考答案 第 4 页 共 6 页 Y = n ”表示前 n − 1 次试验只成功了1次，且第 n 次试验成功， 1 2 1 n−1 2 故P(Y =n)=C1  ( )n−2 = ( )n−2，-------------------------------------------9分 n−1 3 3 3 9 3 当 n 为偶数时， 所以 P ( A B ) = P ( 2 ) + P ( 4 ) + … … + P ( n ) = 1 9 [1  ( 2 3 ) 0 + 3  ( 2 3 ) 2 + … + ( n − 1 )  ( 2 3 ) n − 2 ] ， 2 2 2 令S =1( )0 +3( )2 +…+(n−1)( )n−2 n 3 3 3 则 4 9 S n = 1  ( 2 3 ) 2 + 3  ( 2 3 ) 4 + … + ( n − 1 )  ( 2 3 ) n ， 两式相减得： 5 9 S n = 1 + 2 [ ( 2 3 ) 2 + ( 2 3 ) 4 + … + ( 2 3 ) n − 2 ] − ( n − 1 )  ( 2 3 ) n -----------------------13分 则 S n = 1 1 2 7 5 − ( 2 3 ) n  ( 1 1 2 7 5 + 9 5 n ) ．即 P ( A B ) = 1 2 3 5 − ( 1 2 3 5 + 1 5 n )  ( 2 3 ) n . 当n为奇数时，同理可得 1 2 2 2 13 1 8 2 P(AB)=P(2)+P(4)+……+P(n−1)= [1( )0 +3( )2 +…+(n−2)( )n−3]= −( n+ )( )n−1 9 3 3 3 25 5 25 3 综上， P ( A B ) =  1 21 2 3 53 5 − − ( ( 1 51 5 n n + + 8 2 5 1 3 2 5 ) )   ( ( 2 32 3 ) ) n n − 1 , n 为 , n 为 偶 奇 数 数 --------------------------------------------17分 （注：只考虑n是奇数或偶数，且答案正确扣2分） 19．（本题共17分）解： （1）由双曲线方程 x a 2 2 − 4 y − 2 a 2 = 1 ，则  a 4 2 −  a 0 2  0 ，得到 a  ( 0 , 2 ) ， 联立抛物线与双曲线方程  x ay 2 2 2 − = 44 2 y − a x − 2 4 = 1 ，得到 ( 4 − a 2 ) x 2 − 4 a 2 x + a 4 = 0 ，-----2分 记 f ( x ) = ( 4 − a 2 ) x 2 − 4 a 2 x + a 4 = [ ( 2 + a ) x − a 2 ] [ ( 2 − a ) x − a 2 ] a2 ，可知 f(x)=0有两个根 a+2 和 2 a − 2 a a2 a2 ，其中 1，则 1，解得a(1,2).-----------------------------6分 a+2 2−a 又直线 A F 分别交 C 1 , C 2 于C,D（不同于 A , B 点），即 A , B , F 三点不共线，当x=2时，代入 4 4 抛物线方程得到A(2,2)，将A(2,2)代入双曲线方程得到 − =1，解得 a2 4−a2 a 2 = 6 − 2 5 ， 故a= 5−1. 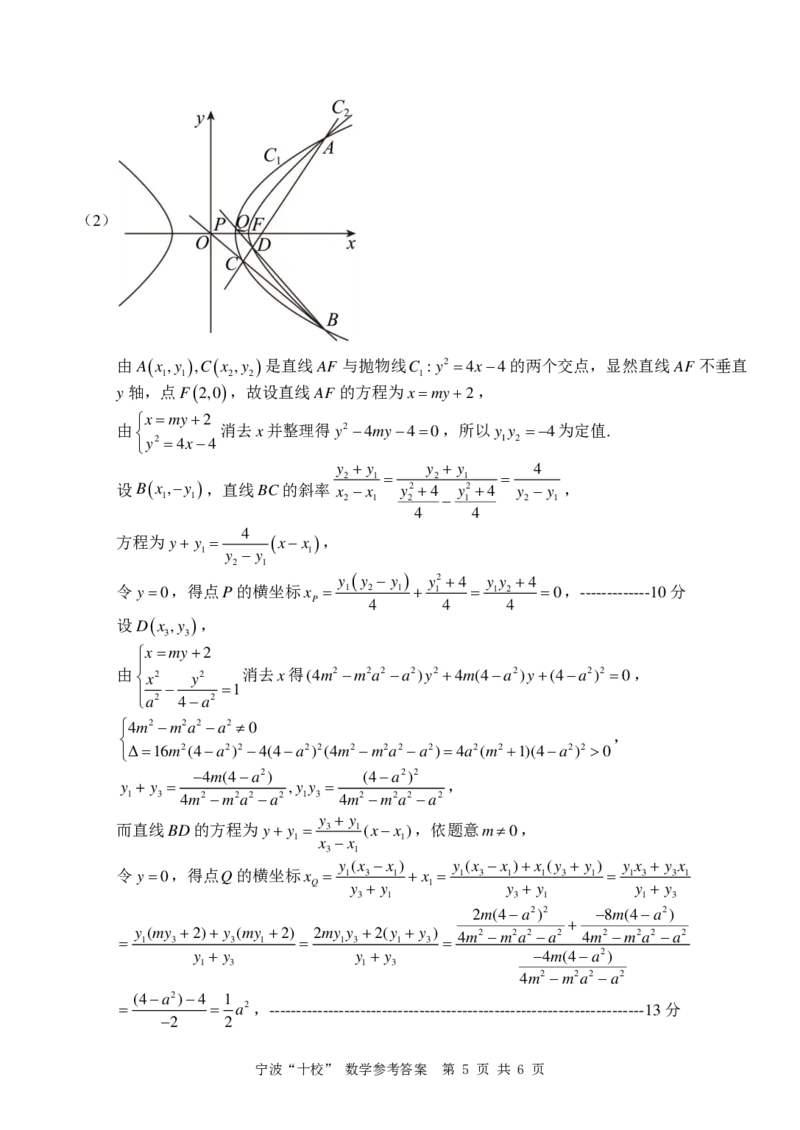综上，a(1, 5−1)( 5−1,2)------------------------------------------------------------------7分（2） 由 宁波“十校” 数学参考答案 第 5 页 共 6 页 A ( x 1 , y 1 ) , C ( x 2 , y 2 ) 是直线 A F 与抛物线 C 1 : y 2 = 4 x − 4 的两个交点，显然直线 A F 不垂直 y轴，点 F ( 2 , 0 ) ，故设直线 A F 的方程为 x = m y + 2 ， 由  x y = 2 m = y 4 x + − 2 4 消去x并整理得 y 2 − 4 m y − 4 = 0 ，所以 y 1 y 2 = − 4 为定值. 设 B ( x 1 , − y 1 ) ，直线 B C 的斜率 y x 2 2 + − y x 1 1 = y 22 + 4 y 24 + − y y 121 + 4 4 = y 2 4 − y 1 ， 方程为 y + y 1 = y 2 4 − y 1 ( x − x 1 ) ， 令 y = 0 ，得点 P 的横坐标 x P = y 1 ( y 2 4 − y 1 ) + y 21 + 4 4 = y 1 y 24 + 4 = 0 ，-------------10分 设D(x ,y )， 3 3 由  x x a = 2 2 m − y 4 + y − 2 2 a 2 = 1 消去 x 得 ( 4 m 2 − m 2 a 2 − a 2 ) y 2 + 4 m ( 4 − a 2 ) y + ( 4 − a 2 ) 2 = 0 ， 4m2 −m2a2 −a2 0  ， Δ=16m2(4−a2)2 −4(4−a2)2(4m2 −m2a2 −a2)=4a2(m2 +1)(4−a2)2 0 y 1 + y 3 = 4 m − 4 2 m − ( m 4 2 − a a 2 2 − ) a 2 , y 1 y 3 = 4 m ( 2 4 − − m a 2 2 a ) 2 2 − a 2 ， 而直线BD的方程为 y + y 1 = y x 3 3 + − y x 1 1 ( x − x 1 ) ，依题意 m  0 ， 令 y = 0 ，得点 Q y (x −x ) y (x −x )+x (y + y ) y x + y x 的横坐标x = 1 3 1 +x = 1 3 1 1 3 1 = 1 3 3 1 Q y + y 1 y + y y + y 3 1 3 1 1 3 2m(4−a2)2 −8m(4−a2) + y (my +2)+ y (my +2) 2my y +2(y + y ) 4m2 −m2a2 −a2 4m2 −m2a2 −a2 = 1 3 3 1 = 1 3 1 3 = y + y y + y −4m(4−a2) 1 3 1 3 4m2 −m2a2 −a2 (4−a2)−4 1 = = a2，----------------------------------------------------------------------13分 −2 2因此 宁波“十校” 数学参考答案 第 6 页 共 6 页 | Q F |= 2 − 1 2 a 2 ， | P Q |= 1 2 a 2 . 联立抛物线与双曲线方程  x ay 2 2 2 − = 44 y −x 2 a − 2 4 = 1 ，得到 ( 4 − a 2 ) x 2 − 4 a 2 x + a 4 = 0 ，解得点 A 的坐标 ( 2 a − 2 a , 2 ( a + 2 2 ) − ( a a − 1 ) ) ，由 y 1 y 2 = − 4 ， y 2 = − y 4 1 = ( a + − 2 2 2 ) − ( a a − 1 ) . 根据 S 1 = 3 S 2 ，则 S S 1 2 = 1 21 2 | | Q P F Q | |   | | y y A C | | = 3 ，代入得到 ( 2 − 1 2 1 2 a a 2  2 | )  | y 2 y | 1 | = 3 ，即 ( 4 a − 2  a | 2 y ) 1  y y 2 21| = 3 ， 化简得 ( 4 − a 2 )  4 ( a + 2 2 ) − ( a a − 1 ) = 1 2 a 2 解得 a 3 = 4 ，故 a = 3 4 .--------------------17分