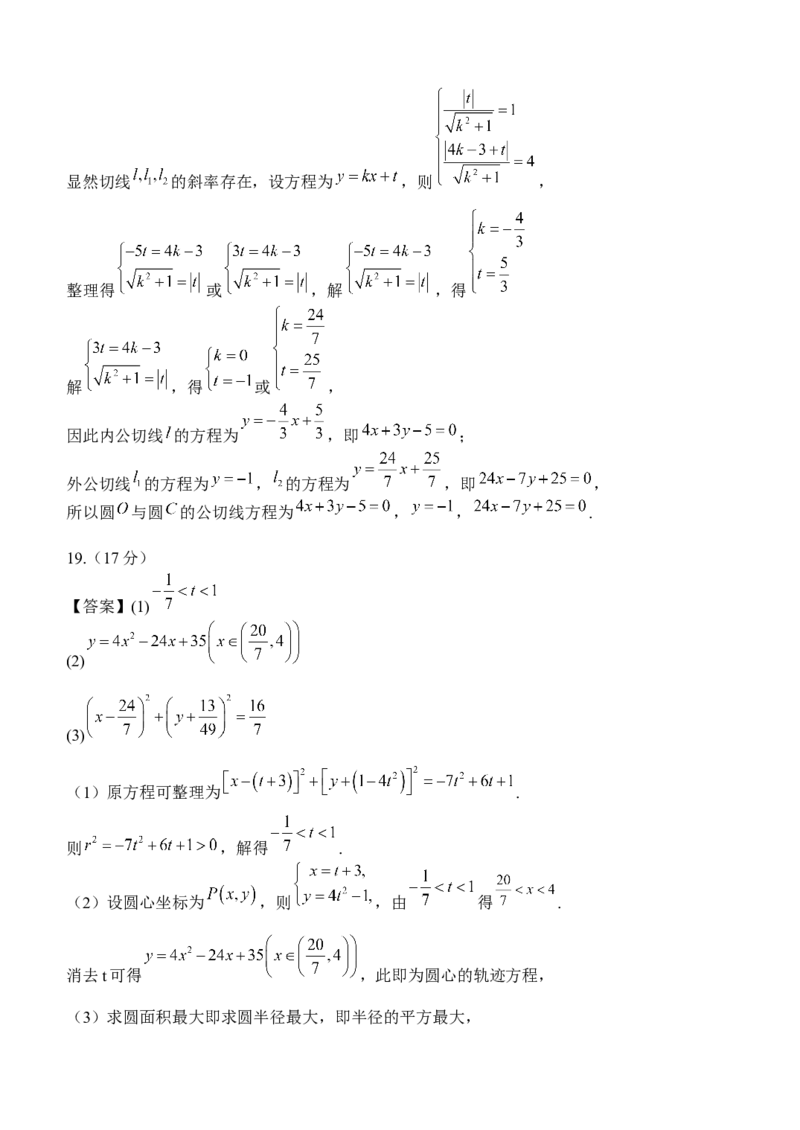文档内容
南阳一中高二年级2025年秋期第一次月考
数学学科答案
一、单选题(每小题5分,共40分)
1.B 2.D 3.C
4.B
【详解】因为 两点横坐标不同,故倾斜角不为 ,
由题意得 ,
因为 ,所以 .
故选:B
5.B
6.C
依题意,由椭圆定义得 ,即 ,
令椭圆 : 的半焦距为c,则F2(c,0),直线AB:x=c,
由 得 ,于是得 ,则 ,
所以椭圆 的方程为 .
故选:C
7.D,应为
8.A【详解】若 的欧拉线方程为 ,设点 ,则 的重心为 ,
显然点 在直线 上,于是得 ,
直线 的斜率为2,线段 的中点 ,则线段 的中垂线方程为 ,即 ,
由 得 的外心 ,即有 ,因此 ,
解得 或 ,于是得点C的坐标为 或 ;
当C的坐标为 时, 的重心为 ,外心为 ,因此 的欧拉线方程
为 ,
所以“ 的欧拉线方程为 ”是“点C的坐标为 ”的必要不充分条件.
故选:A
9.ACD
10.AD
【详解】对于A项,由题意可得 ,所以 ,从而点 在圆 的外
部,故A项正确;
对于B项,直线 恒过定点 , ,
点 在圆的内部,所以直线与圆相交,则最长的弦为直径4,故B项错;
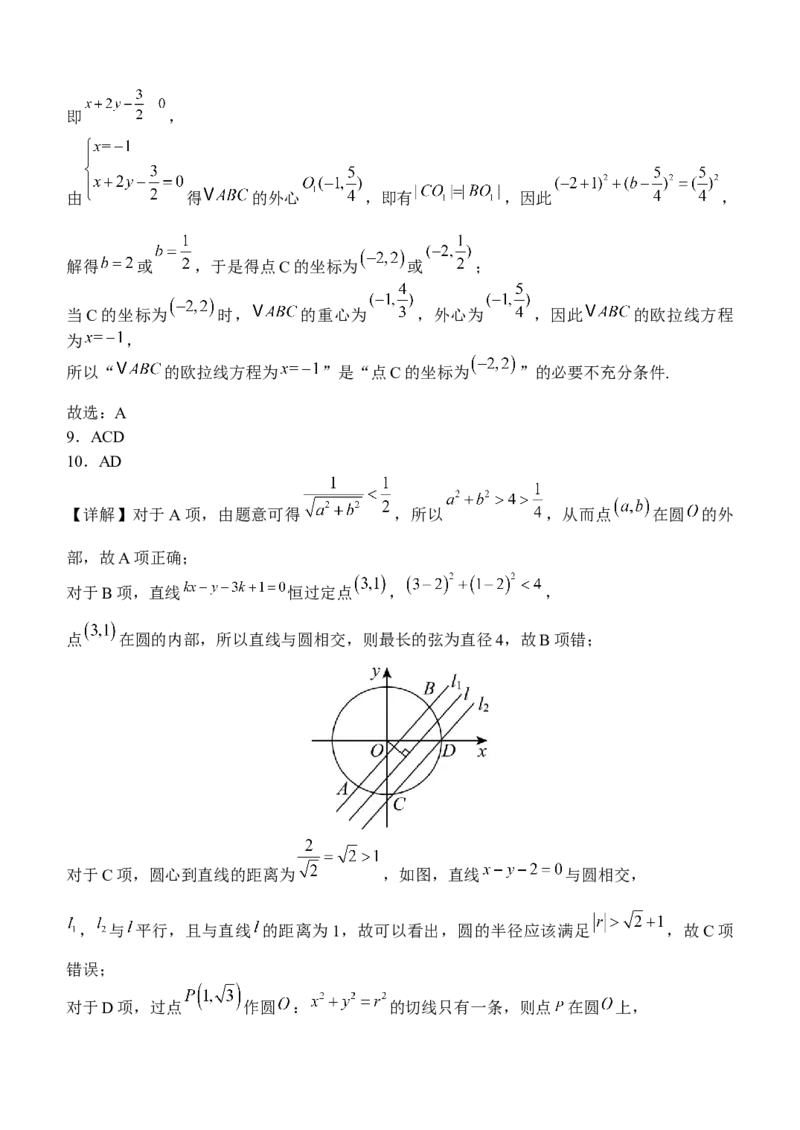
对于C项,圆心到直线的距离为 ,如图,直线 与圆相交,
, 与 平行,且与直线 的距离为1,故可以看出,圆的半径应该满足 ,故C项
错误;
对于D项,过点 作圆 : 的切线只有一条,则点 在圆 上,又 ,故切线的斜率为 ,
所以切线方程为 ,即 ,故D项正确.
故选:AD.
11.ACD
【 详 解 】 圆 的 圆 心 为 半 径
故 正确;
由 题 知
当 时, 取得最小值为 故 错误;
根据向量投影的几何意义,知 在 方向上的投影的取值范围为
故 正确;
若 ,且 ,则 三点共线.
直线 的方程为 圆心 到直线 的距离为
所以直线 与圆相交,故存在两个不同的点 ,使 ,故 正确.
故选: .
三、填空题(每小题5分,共15分)
12.
13. 或14.6
【详解】 变形为 ,
令 ,解得 ,
故 恒过点 ,
设点 ,则 ⊥ ,
即 ,
整理得 ,
所以 点轨迹为以 为圆心, 为半径的圆,
又 ,即 在圆外,
则 的最大值为 .
故答案为:6
四、解答题(共77分)
15.(13分)
(1)
(2) 或 .
(1)解:设圆心为 ,
依题意有 ,解得 或 (舍去),
,则 ,故圆 的标准方程为
(2)若 斜率不存在,则 ,代入圆 方程得 ,
解得 或 , ,符合题意;
若 斜率存在,设斜率为 ,则直线 ,即 ,
由圆心 到直线 的距离为 ,
即 ,所以 , ,即
综上,所求直线 的方程为 或 .
16.(15分)
(1)解:因为 ,而直线 : 的斜率为 ,
所以直线 的斜率为 ,即直线 的方程为: ,即 ,
所以点 在直线 与 边上的中线的交点, ,解得 , ,
所以顶点 的坐标 ,而 为线段 的中点,所以
,即 的坐标 ;
(2)解:当直线 经过原点时,设直线 的方程为 ,将
的坐标 代入可得 ,解得 ,这时直线的方程为
;当直线 不过原点时,设直线 的方程为 ,
将 代入可得 ,解得 ,这时直线 的方程为
,综上所述:直线 的方程为 或 .
17.(15分)(1)
(2)
【详解】(1)直线 的斜率 ,
因为 ,所以直线 的斜率存在,设为 ,且 .
即 ,所以 ,解得 .
将 代入直线 得 ,即 ,
所以 与 之间的距离为 .
(2)若 ,则 ,
由 可知,点 是线段 的中点,
设 ,所以点 关于 的对称点 ,
因为点 在直线 上,
把点 代入 方程 ,即 ,
解得 ,
所以 ,
可得直线斜率 ,所以直线 的方程为 ,即 ,
所以直线 的方程为 .
18.(17分)(1) ;(2) ;
(3) , , .
【详解】(1)圆 的圆心 ,半径为 ,
圆 的圆心 ,半径为4,
由圆 与圆 有两个不同的交点,得 ,而 ,
因此 ,解得 ,
所以 的取值范围是 .
(2)当 时,圆 ,此时圆 与圆 相交,两圆方程相减得直线 方程
,
点 到直线 的距离 ,
所以 .
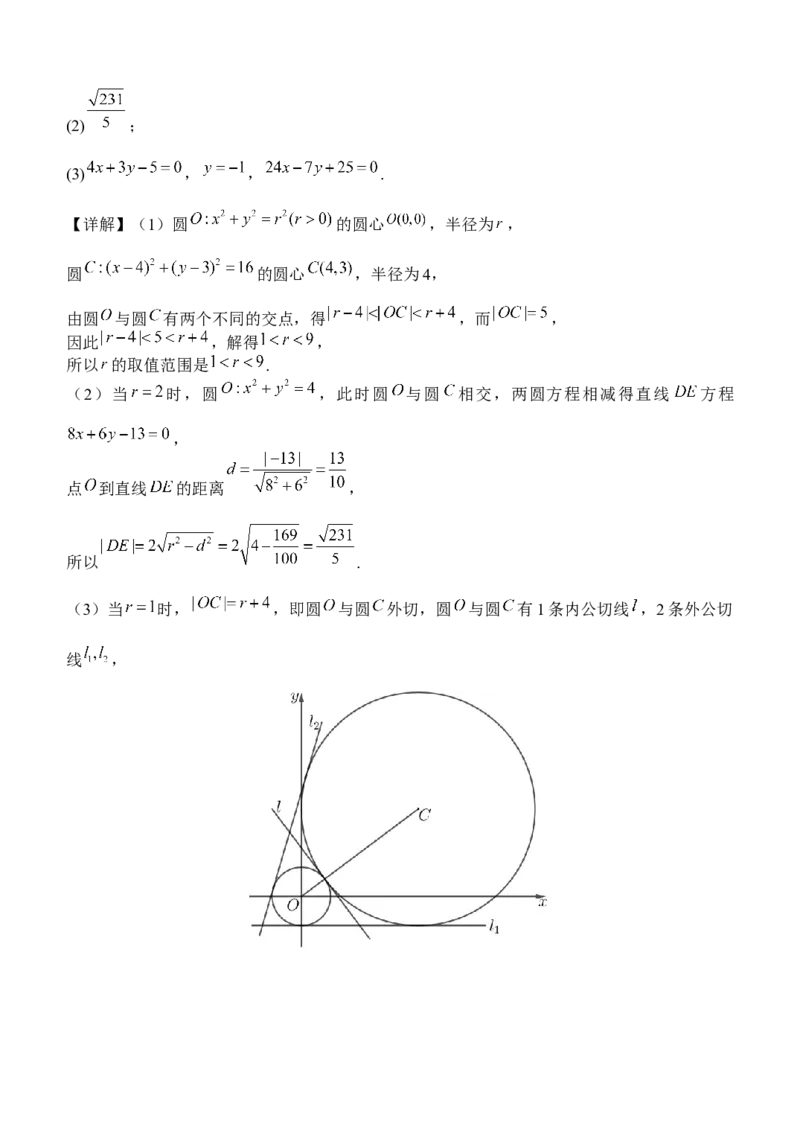
(3)当 时, ,即圆 与圆 外切,圆 与圆 有1条内公切线 ,2条外公切
线 ,显然切线 的斜率存在,设方程为 ,则 ,
整理得 或 ,解 ,得
解 ,得 或 ,
因此内公切线 的方程为 ,即 ;
外公切线 的方程为 , 的方程为 ,即 ,
所以圆 与圆 的公切线方程为 , , .
19.(17分)
【答案】(1)
(2)
(3)
(1)原方程可整理为 .
则 ,解得 .
(2)设圆心坐标为 ,则 ,由 得 .
消去t可得 ,此即为圆心的轨迹方程,
(3)求圆面积最大即求圆半径最大,即半径的平方最大,则 , .
所以当 时, 的最大值为 ,此时圆的方程为 .