郑州二测数学答案_2024年3月_013月合集_2024届河南省郑州市周口市高三下学期第二次质量预测（郑州周口二测）

郑州市 2024 高三第二次质量预测数学（参考答案） 一、单选题 题号 1 2 3 4 5 6 7 8 答案 B D C B D C C A 二、多选题 题号 9 10 11 答案 AD ABD ACD 三、填空题 1  12. 4 4 5 13. 10， 5 14. 22ln2 四、解答题 15.解：(1)前3局比赛甲都不下场说明前3局甲都获胜， 1 1 1 1 故前3局甲都不下场的概率为P    . ...........................4分 2 2 2 8 (2)X 的所有可能取值为0，1，2，3. ...........................5分 1 1 1 其中， X 0表示第1局乙输，第3局是乙上场，且乙输，则P(X 0)   ； 2 2 4 ...........................6分 X 1表示第1局乙输，第3局是乙上场，且乙赢；或第1局乙赢，且第2局乙输， 1 1 1 1 1 则P(X 1)     ； ............................8分 2 2 2 2 2 X  2表示第1局乙赢，且第2局乙赢，第3局乙输， 1 1 1 1 则P(X 2)    ； ...........................9分 2 2 2 8 X 3表示第1局乙赢，且第2局乙赢，第3局乙赢， 1 1 1 1 则P(X 3)    ； ...........................10分 2 2 2 8 所以X的分布列为 X 0 1 2 3 1 1 1 1 P 4 2 8 8 1 {#{QQABCQKEogAAAIJAARgCUQGACEEQkBCAAIoGhBAEsAAACBNABAA=}#}...........................11分 1 1 1 1 9 故X的数学期望为E(X)0 1 2 3  . ...........................13分 4 2 8 8 8 2ax2 (12a2)xa f(x) 16. 解： (1) 函数定义域为 (0,) ， x , ...........................2分 因为x 1是函数 y  f(x) 的极值点， 1 所以 f(1)1a2a2 0，解得a   或a 1， 2 因为a 0，所以a 1. ...........................5分 2x2 x1 2x1x1 此时 fx  x x 令 fx0得x 1，令 fx0得0 x1， ∴ f(x)在（0,1）单调递减，在（1,）单调递增，所以x 1是函数的极小值点. 所以a 1. ...........................7分 (2)当a 0时， f(x) x，则函数 f x的单调增区间为(0,); ...........................8分 2ax2 (12a2)xa (2ax1)(xa) 当a 0时， f(x)  ， ...........................9分 x x 因为a 0，x0，则2ax10， 令 f(x) 0得x  a；令 f(x) 0 得0 x a ; 函数的单调减区间为(0,a),单调增区间为(a,). ...........................13分 综上可知：当a 0时，函数 f x在(0,)上单调递增，无递减区间； 当a 0时，函数 f x在(0,a)上单调递减，在 (a,) 上单调递增. 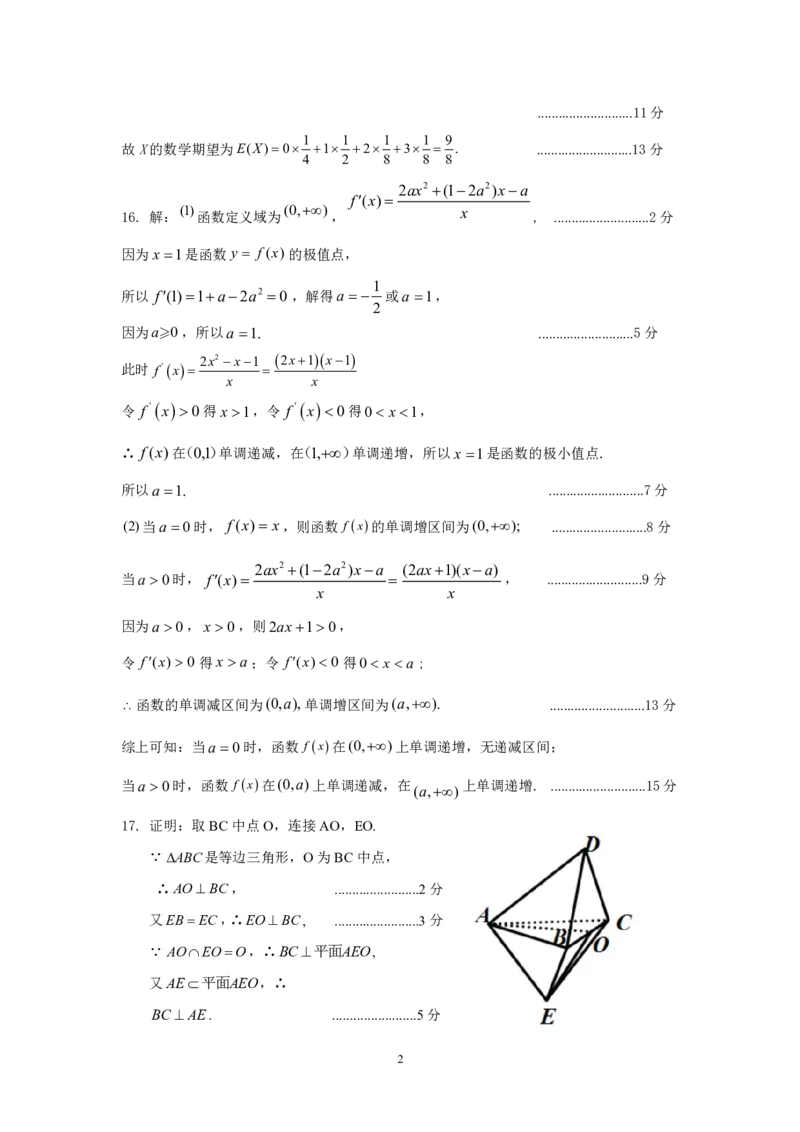...........................15分 17. 证明：取BC中点O，连接AO，EO. ABC是等边三角形，O为BC中点， ∴AOBC， ........................2分 又EBEC，∴EOBC, ........................3分  AOEOO，∴BC平面AEO, 又AE平面AEO，∴ BCAE. ........................5分 2 {#{QQABCQKEogAAAIJAARgCUQGACEEQkBCAAIoGhBAEsAAACBNABAA=}#}(2)连接DO，则DO⊥BC， 由AB ACBC2，DBDCEBEC 2得 AO 3，DO1， 又AD2，AO2DO2  AD2， DOAO, .......................8分 又AOBCO， DO平面ABC . ........................9分 如图，以O为坐标原点，OA，OB，OD所在直线分别为x,y,z轴，建立空间直角坐标系Oxyz， 则O(0,0,0)，A( 3,0,0)，C(0,1,0)，D(0,0,1)，   ∴CA( 3,1,0)，CD(0,1,1), ......................................10分     nCA0,  3xy0, 设平面ACD的法向量为n(x,y,z)，则  即 nCD0, yz0,  取x1，则n(1, 3, 3). ........................................12分 ∵AOE是二面角ABCE的平面角，∴AOE30， ........................................13分 3 1  3 3 又OE1，∴E( ,0, ),DE( ,0, ), ........................................14分 2 2 2 2     DEn 7 则cosDE,n    , ........................................16分 DE n 7 7 ∴直线DE与平面ACD所成角的正弦值为 . ........................................17分 7 18.解：（1）依题意有b1,c 3，解得a2 b2 c2 4， x2 所以椭圆的方程为  y2 1. ........................................4分 4 1 （2）设l :xmy1(m0), A(x ,y ),B(x ,y ),则l :x y1(m0), AB 1 1 2 2 CD m xmy1 联立 ,故(m2 4)y2 2my30， x2 4y2 4 2m 16m2480， y  y  ， ........................................6分 1 2 m2 4 3 {#{QQABCQKEogAAAIJAARgCUQGACEEQkBCAAIoGhBAEsAAACBNABAA=}#}4 m 故M( , )， ........................................7分 m2 4 m2 4 1 4m2 m 由 代替m，得N( , )， ........................................8分 m 14m2 14m2 4 4m2 4 4 当  ,即m2 1时，l :x ，过点K( ,0) . m2 4 14m2 MN 5 5 4 4m2 当  ,即m2 1时， m2 4 14m2 5m m 5m 4 K  ，l :y  (x )(m2 1,m0), MN 4(m2 1) MN m2 4 4(m2 1) m2 4 4(m2 1) 4 4m2 16 4 令 y0,x    ， 5(m2 4) (m2 4) 5(m2 4) 5 4 ∴直线MN恒过点K( ,0). 5 4 当m0,经验证直线MN过点K( ,0). 5 4 综上，直线MN恒过点K( ,0). ........................................12分 5 (3) 1 1 1 m m 1 |m3 m| S S S  |KS|| y  y |   |  |  MNS MKS NKS 2 M N 2 5 14m2 m2 4 2 4m4 17m2 4 1 |m | 1 m   , 2 4 4m2  17 m2 ........................................14分 1 |m | 令t|m 1 |[2,)，S  1  m  1  t  1  1 m MNS 2 4 2 4t2 9 2 9 4m2  17 4t m2 t ， 1 ∵S 在t[2,)上单调递减，∴S  ， .........................................16分 MNS MNS 25 当且仅当t2,m1,时取等号. 1 故MNS面积的最大值为 . ........................................17分 25 19. 解：（1）由题意得a a a 4，则1124或134， 1 2 n 故所有4的1增数列有数列1,2,1和数列1，3. ............................................3分 （2）当n5时，因为存在m的6增数列， 所以数列{a }的各项中必有不同的项，所以m6且mN*. n 4 {#{QQABCQKEogAAAIJAARgCUQGACEEQkBCAAIoGhBAEsAAACBNABAA=}#}若m6，满足要求的数列{a }中有四项为1，一项为2， n 所以k4，不符合题意，所以m6. 若 m7 ，满足要求的数列{a n }中有三项为1，两项为2，符合m的6增数列. 所以，当n5时，若存在m的6增数列，m的最小值为7. .........................8分 （3）若数列{a }中的每一项都相等，则k 0， n 若k 0，所以数列{a }中存在大于1的项， n 若首项a 1，将a 拆分成a 个1后k变大， 1 1 1 所以此时k不是最大值，所以a 1. 1 当i2,3,...,n时，若a a ，交换a,a 的顺序后k变为k1， i i1 i i1 所以此时k不是最大值，所以a a . i i1 若a a 0,1，所以a a 2， i1 i i1 i 所以将a 改为a 1，并在数列首位前添加一项1，所以k的值变大， i1 i1 所以此时k不是最大值，所以a a 0,1 . i1 i 若数列{a }中存在相邻的两项a 2,a 3，设此时{a }中有x项为2， n i i1 n 将a 改为2，并在数列首位前添加a 2个1后，k的值至少变为k1， i1 i1 所以此时k不是最大值， 所以数列{a }的各项只能为1或2，所以数列{a }为1,1,...,1,2,2,,2的形式. n n 设其中有x项为1，有y项为2， 因为存在100的k增数列，所以x2y100， 所以k xy1002yy2y2100y2(y25)21250， 所以，当且仅当x50,y25时，k取最大值为1250. .........................17分 5 {#{QQABCQKEogAAAIJAARgCUQGACEEQkBCAAIoGhBAEsAAACBNABAA=}#}