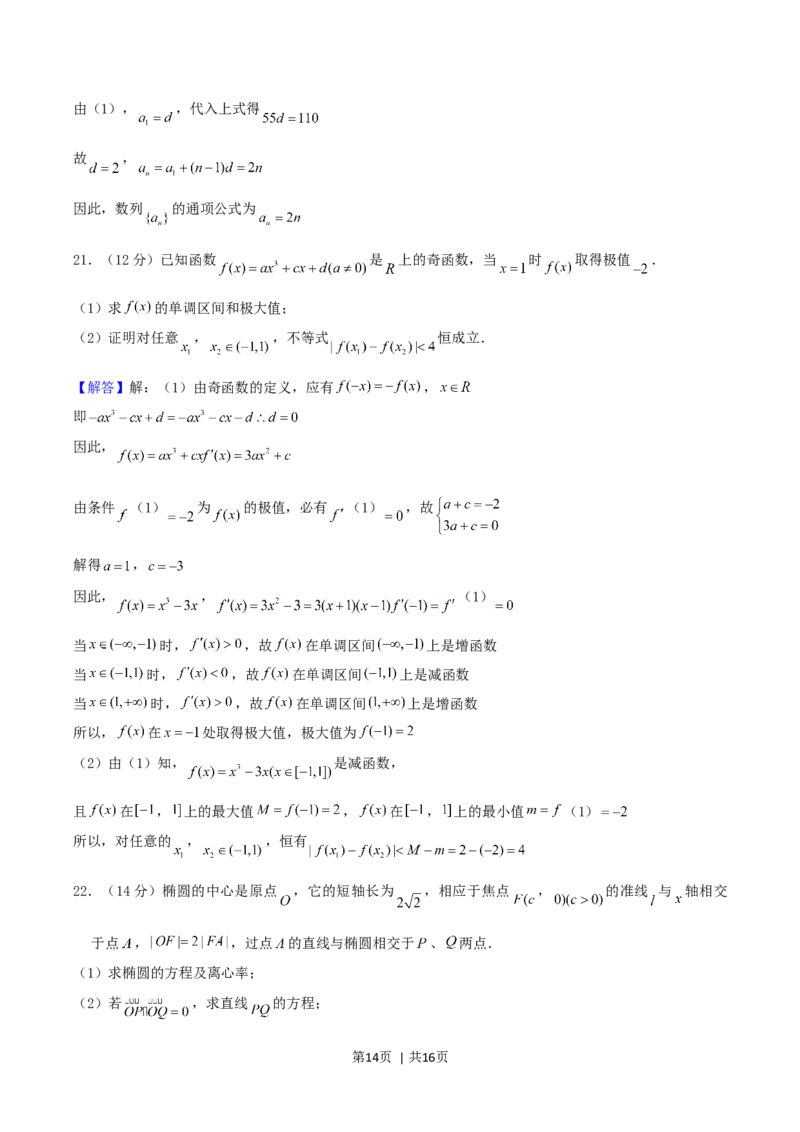2004年天津市高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·word_天津

2004 年天津市高考文科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）设集合 ，2，3，4，5， ， ，那么下列结论正确的是 A． B． C． D． 2．（5分）不等式 的解集为 A． ， B． ， C． ， D． ， 3．（5分）对任意实数 、 、 ，在下列命题中，真命题是 A．“ ”是“ ”的必要条件 B．“ ”是“ ”的必要条件 C．“ ”是“ ”的充分条件 D．“ ”是“ ”的充分条件 4．（5分）若平面向量 与向量 的夹角是 ，且 ，则 A． B． C． D． 5．（5分）设 是双曲线 上一点，该双曲线的一条渐近线方程是 ， ， 分别是 双曲线的左、右焦点，若 ，则 等于 A．2 B．18 C．2或18 D．16 6．（5分）若函数 在区间 ， 上的最大值是最小值的3倍，则 等于 A． B． C． D． 7．（5分）若过定点 且斜率为 的直线与圆 在第一象限内的部分有交点，则 的取值范围是 A． B． C． D． 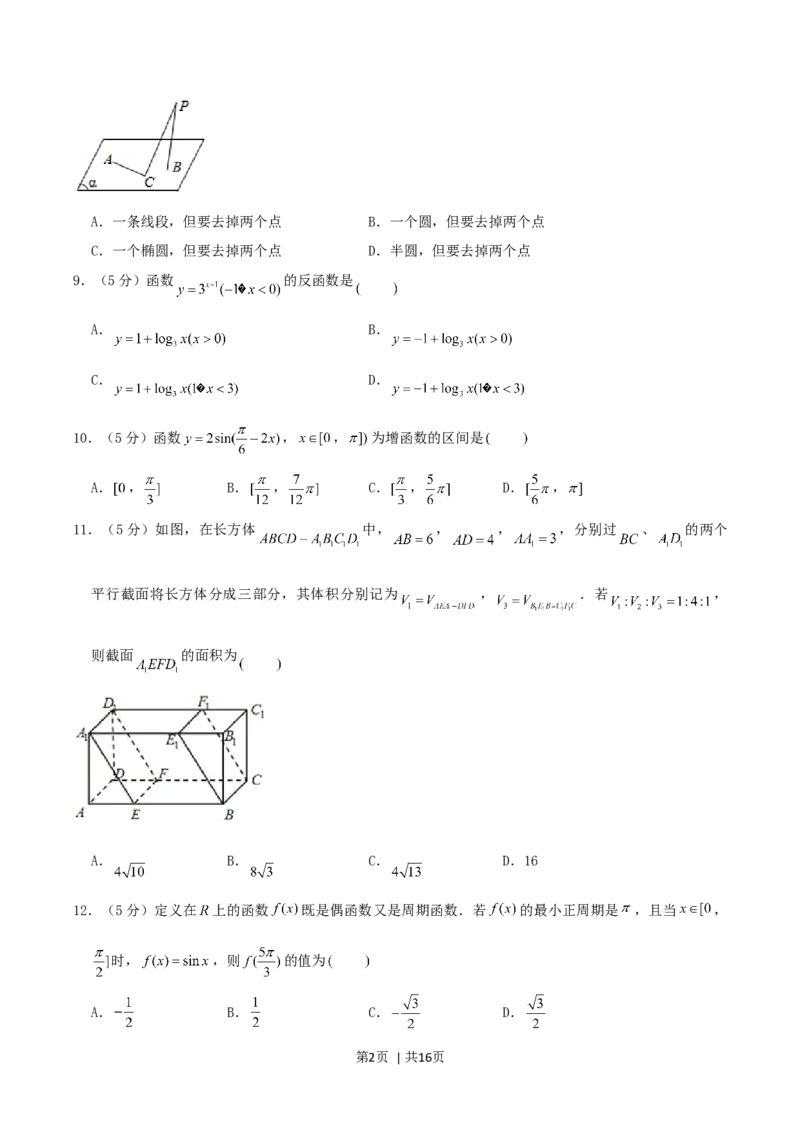8．（5分）如图，定点 和 都在平面 内，定点 ， ， 是 内异于 和 的动点，且 ．那么，动点 在平面 内的轨迹是 第1页 | 共16页A．一条线段，但要去掉两个点 B．一个圆，但要去掉两个点 C．一个椭圆，但要去掉两个点 D．半圆，但要去掉两个点 9．（5分）函数 的反函数是 A． B． C． D． 10．（5分）函数 ， ， 为增函数的区间是 A． ， B． ， C． ， D． ， 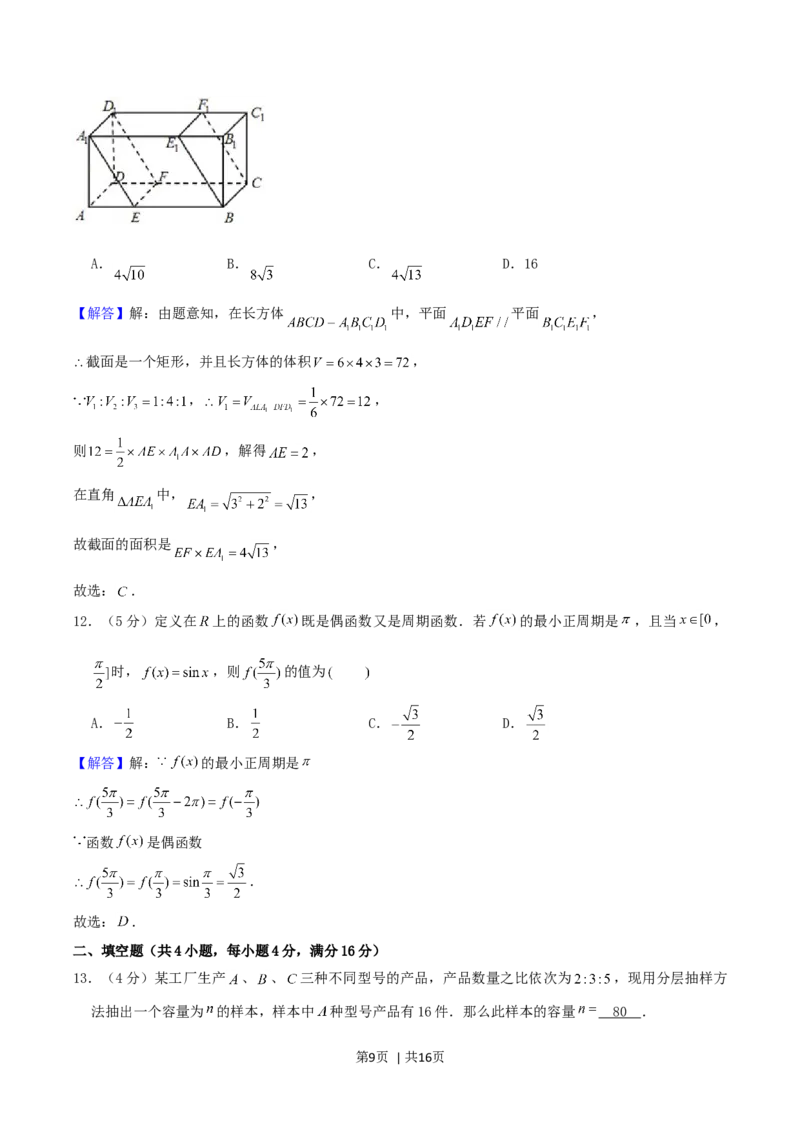11．（5分）如图，在长方体 中， ， ， ，分别过 、 的两个 平行截面将长方体分成三部分，其体积分别记为 ， ．若 ， 则截面 的面积为 A． B． C． D．16 12．（5分）定义在 上的函数 既是偶函数又是周期函数．若 的最小正周期是 ，且当 ， 时， ，则 的值为 A． B． C． D． 第2页 | 共16页二、填空题（共4小题，每小题4分，满分16分） 13．（4分）某工厂生产 、 、 三种不同型号的产品，产品数量之比依次为 ，现用分层抽样方 法抽出一个容量为 的样本，样本中 种型号产品有16件．那么此样本的容量 ． 14．（4分）已知向量 ， ，若 与 垂直，则实数 等于 ． 15．（4分）如果过两点 和 的直线与抛物线 没有交点，那么实数 的取值范围 是 ． 16．（4分）从0，1，2，3，4，5中任取3个数字，组成没有重复数字的三位数，其中能被5整除的三位 数共有 个．（用数字作答） 三、解答题（共6小题，满分74分） 17．（12分）已知 ． （Ⅰ）求 的值； （Ⅱ）求 的值． 18．（12分）从4名男生和2名女生中任选3人参加演讲比赛． （1）求所选3人都是男生的概率； （2）求所选3人中恰有1名女生的概率； （3）求所选3人中至少有1名女生的概率． 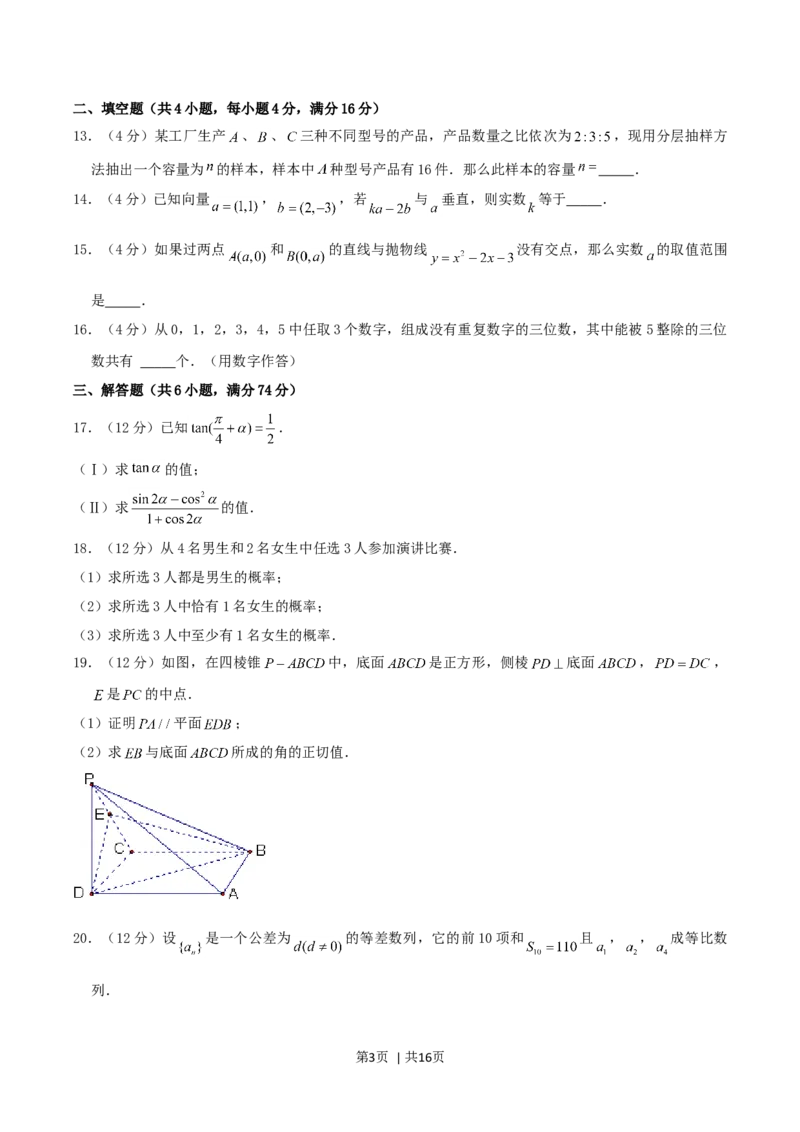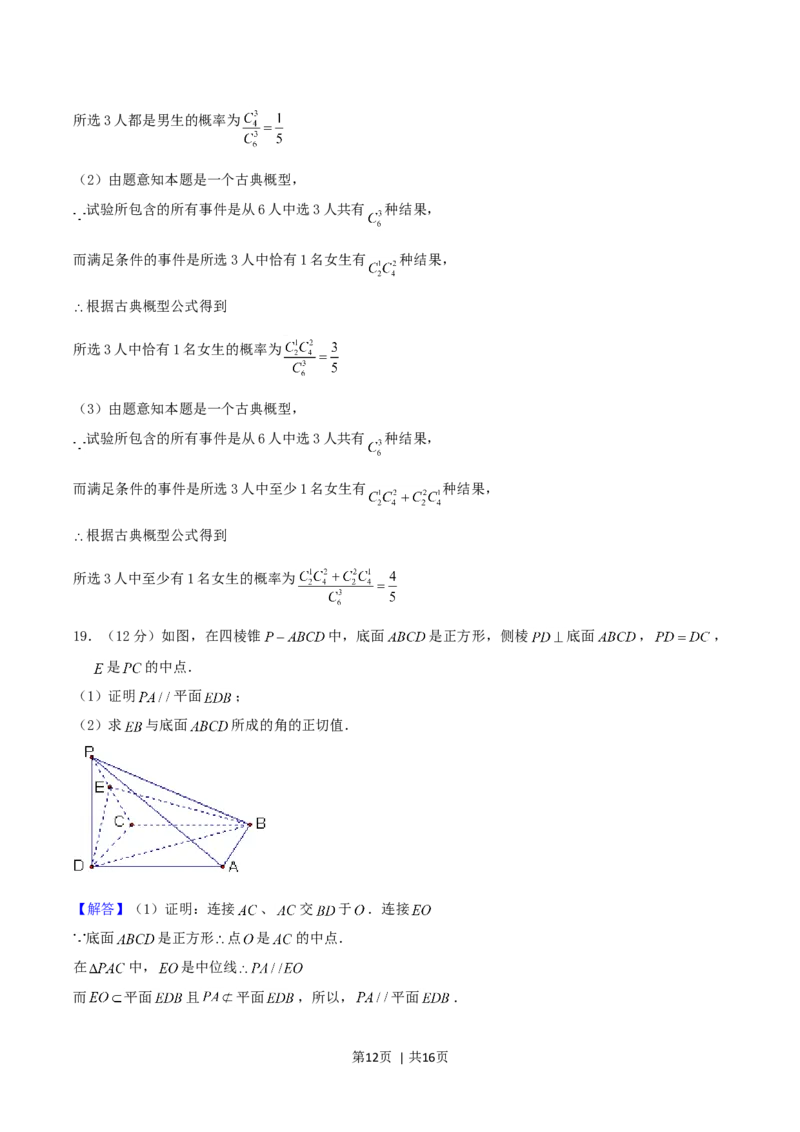19．（12分）如图，在四棱锥 中，底面 是正方形，侧棱 底面 ， ， 是 的中点． （1）证明 平面 ； （2）求 与底面 所成的角的正切值． 20．（12分）设 是一个公差为 的等差数列，它的前10项和 且 ， ， 成等比数 列． 第3页 | 共16页（1）证明 ； （2）求公差 的值和数列 的通项公式． 21．（12分）已知函数 是 上的奇函数，当 时 取得极值 ． （1）求 的单调区间和极大值； （2）证明对任意 ， ，不等式 恒成立． 22．（14分）椭圆的中心是原点 ，它的短轴长为 ，相应于焦点 ， 的准线 与 轴相交 于点 ， ，过点 的直线与椭圆相交于 、 两点． （1）求椭圆的方程及离心率； （2）若 ，求直线 的方程； （3）设 ，过点 且平行于准线 的直线与椭圆相交于另一点 ，证明 ． 第4页 | 共16页2004年天津市高考数学试卷（文科） 参考答案与试题解析 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）设集合 ，2，3，4，5， ， ，那么下列结论正确的是 A． B． C． D． 【解答】解： ，3，4，5， ， 故 、 错误， 故 正确． 故选： ． 2．（5分）不等式 的解集为 A． ， B． ， C． ， D． ， 【解答】解： 故选： ． 3．（5分）对任意实数 、 、 ，在下列命题中，真命题是 A．“ ”是“ ”的必要条件 B．“ ”是“ ”的必要条件 C．“ ”是“ ”的充分条件 D．“ ”是“ ”的充分条件 【解答】解： 、 当 时，“ ”即不是“ ”的必要条件也不是充分条件，故 ， 不成 立； 、 当 时 一定有 ． 但 时，且 时， ， 可以不相等． 即“ ”是“ ”的必要条件． 、当 时，“ ”是“ ”的充分条件不成立； 故选： ． 第5页 | 共16页4．（5分）若平面向量 与向量 的夹角是 ，且 ，则 A． B． C． D． 【解答】解 向量 与向量 的夹角是 ， 向量 与向量 反向， 令 （则 ， 又 ， 解得 故 故选： ． 5．（5分）设 是双曲线 上一点，该双曲线的一条渐近线方程是 ， ， 分别是 双曲线的左、右焦点，若 ，则 等于 A．2 B．18 C．2或18 D．16 【解答】解：整理准线方程得 ， ， ， 或 或18， 故选： ． 6．（5分）若函数 在区间 ， 上的最大值是最小值的3倍，则 等于 A． B． C． D． 【解答】解： ， 是减函数． 第6页 | 共16页． ． ． ． ． 故选： ． 7．（5分）若过定点 且斜率为 的直线与圆 在第一象限内的部分有交点，则 的取值范围是 A． B． C． D． 【解答】解：圆的方程可变形为 ，圆心 ，半径等于3，令 ，则 ． 设 ， ． 又 直线过第一象限且过 点， ．又直线与圆在第一象限内有相交点， ， ，故选 ． 8．（5分）如图，定点 和 都在平面 内，定点 ， ， 是 内异于 和 的动点，且 ．那么，动点 在平面 内的轨迹是 A．一条线段，但要去掉两个点 B．一个圆，但要去掉两个点 C．一个椭圆，但要去掉两个点 D．半圆，但要去掉两个点 【解答】解： 又 面 第7页 | 共16页动点 在平面 内的轨迹是以 为直径的一个圆，但要去掉 、 两个点 故选： ． 9．（5分）函数 的反函数是 A． B． C． D． 【解答】解：由 解得： ， 函数 的反函数是 故选： ． 10．（5分）函数 ， ， 为增函数的区间是 A． ， B． ， C． ， D． ， 【解答】解：由 其增区间可由 的减区间得到， 即 ， ， ． 令 ， ， 故选： ． 11．（5分）如图，在长方体 中， ， ， ，分别过 、 的两个 平行截面将长方体分成三部分，其体积分别记为 ， ．若 ， 则截面 的面积为 第8页 | 共16页A． B． C． D．16 【解答】解：由题意知，在长方体 中，平面 平面 ， 截面是一个矩形，并且长方体的体积 ， ， ， 则 ，解得 ， 在直角 中， ， 故截面的面积是 ， 故选： ． 12．（5分）定义在 上的函数 既是偶函数又是周期函数．若 的最小正周期是 ，且当 ， 时， ，则 的值为 A． B． C． D． 【解答】解： 的最小正周期是 函数 是偶函数 ． 故选： ． 二、填空题（共4小题，每小题4分，满分16分） 13．（4分）某工厂生产 、 、 三种不同型号的产品，产品数量之比依次为 ，现用分层抽样方 法抽出一个容量为 的样本，样本中 种型号产品有16件．那么此样本的容量 8 0 ． 第9页 | 共16页【解答】解： 故答案是80 14．（4分）已知向量 ， ，若 与 垂直，则实数 等于 ． 【解答】解： 向量 ， ，若 与 垂直， ，即： ， ， ， ， ． 15．（4分）如果过两点 和 的直线与抛物线 没有交点，那么实数 的取值范围 是 ． 【解答】解：过 、 两点的直线为： 与抛物线 联立得： ． 因为直线与抛物线没有交点，则方程无解． 即△ ， 解之得 ． 故答案为： 16．（4分）从0，1，2，3，4，5中任取3个数字，组成没有重复数字的三位数，其中能被5整除的三位 数共有 3 6 个．（用数字作答） 【解答】解：其中能被5整除的三位数末位必为0或5． ①末位为0的三位数其首次两位从 的5个数中任取2个排列而成方法数为 ， ②末位为5的三位数，首位从非0，5的4个数中选1个，有 种挑法，再挑十位，还有 种挑法， 合要求的数有 种． 共有 个合要求的数． 三、解答题（共6小题，满分74分） 第10页 | 共16页17．（12分）已知 ． （Ⅰ）求 的值； （Ⅱ）求 的值． 【解答】解：（Ⅰ）解： ， 由 ，有 ，解得 ； （Ⅱ）解法一： ． 解法二：由（1）， ，得 ， 于是 ， 代入得 ． 18．（12分）从4名男生和2名女生中任选3人参加演讲比赛． （1）求所选3人都是男生的概率； （2）求所选3人中恰有1名女生的概率； （3）求所选3人中至少有1名女生的概率． 【解答】解：（1）由题意知本题是一个古典概型， 试验所包含的所有事件是从6人中选3人共有 种结果， 而满足条件的事件是所选3人都是男生有 种结果， 根据古典概型公式得到 第11页 | 共16页所选3人都是男生的概率为 （2）由题意知本题是一个古典概型， 试验所包含的所有事件是从6人中选3人共有 种结果， 而满足条件的事件是所选3人中恰有1名女生有 种结果， 根据古典概型公式得到 所选3人中恰有1名女生的概率为 （3）由题意知本题是一个古典概型， 试验所包含的所有事件是从6人中选3人共有 种结果， 而满足条件的事件是所选3人中至少1名女生有 种结果， 根据古典概型公式得到 所选3人中至少有1名女生的概率为 19．（12分）如图，在四棱锥 中，底面 是正方形，侧棱 底面 ， ， 是 的中点． （1）证明 平面 ； （2）求 与底面 所成的角的正切值． 【解答】（1）证明：连接 、 交 于 ．连接 底面 是正方形 点 是 的中点． 在 中， 是中位线 而 平面 且 平面 ，所以， 平面 ． 第12页 | 共16页（2）解：作 交 于 ．连接 ，设正方形 的边长为 ． 底面 ， 为 的中点 底面 ， 为 在底面 内的射影，故 为直线 与底面 所成的角． 在 中， 在 中 所以 与底面 所成的角的正切值为 20．（12分）设 是一个公差为 的等差数列，它的前10项和 且 ， ， 成等比数 列． （1）证明 ； （2）求公差 的值和数列 的通项公式． 【解答】（1）证明：因 ， ， 成等比数列，故 而 是等差数列，有 ， 于是 即 化简得 （2）解：由条件 和 ，得到 第13页 | 共16页由（1）， ，代入上式得 故 ， 因此，数列 的通项公式为 21．（12分）已知函数 是 上的奇函数，当 时 取得极值 ． （1）求 的单调区间和极大值； （2）证明对任意 ， ，不等式 恒成立． 【解答】解：（1）由奇函数的定义，应有 ， 即 因此， 由条件 （1） 为 的极值，必有 （1） ，故 解得 ， 因此， ， （1） 当 时， ，故 在单调区间 上是增函数 当 时， ，故 在单调区间 上是减函数 当 时， ，故 在单调区间 上是增函数 所以， 在 处取得极大值，极大值为 （2）由（1）知， 是减函数， 且 在 ， 上的最大值 ， 在 ， 上的最小值 （1） 所以，对任意的 ， ，恒有 22．（14分）椭圆的中心是原点 ，它的短轴长为 ，相应于焦点 ， 的准线 与 轴相交 于点 ， ，过点 的直线与椭圆相交于 、 两点． （1）求椭圆的方程及离心率； （2）若 ，求直线 的方程； 第14页 | 共16页（3）设 ，过点 且平行于准线 的直线与椭圆相交于另一点 ，证明 ． 【解答】（1）解：由题意，可设椭圆的方程为 ． 由已知得 解得 所以椭圆的方程为 ，离心率 ． （2）解：由（1）可得 ． 设直线 的方程为 ．由方程组 得 依题意△ ，得 ． 设 ， ， ， ，则 ，① ．② 由直线 的方程得 ， ．于是 ．③ ， ．④ 由①②③④得 ，从而 ． 所以直线 的方程为 或 （3）证明： ． 第15页 | 共16页由已知得方程组 注意 ，解得 因 ， ， ，故 ． 而 ，所以 ． 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/5/23 23:12:58；用户：15217760367；邮箱：15217760367；学号：10888156 第16页 | 共16页