文档内容
光岳楼与鹳雀楼、黄鹤楼、岳阳楼、太白楼、滕王阁、蓬莱阁、镇海楼、甲秀楼、大观楼共同组成中国十
2024 年高考数学第一次模拟考试(七省新高考 02)
大名楼.其墩台为砖石砌成的正四棱台,如图所示,光岳楼的墩台上底面正方形的边长约为32m,下底面正
高三数学
方形的边长约为34.5m,高的4倍比上底面的边长长4m,则光岳楼墩台的体积约为( )
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准
考证号填写在答题卡上.
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.
3.回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.
A. B. C. D.
4.测试范围:高考全部内容
5.考试结束后,将本试卷和答题卡一并交回. 6.《红海行动》是一部现代海军题材影片,该片讲述了中国海军“蛟龙突击队”奉命执行撤侨任务的故事.
撤侨过程中,海军舰长要求队员们依次完成六项任务,并对任务的顺序提出了如下要求:重点任务B必须
第Ⅰ卷(选择题)
排在前三位,且任务A、D必须排在一起,则这六项任务的不同安排方案共有( )
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。 A.240种 B.188种 C.156种 D.120种
1.已知集合 , ,则 ( )
7.已知 ,则 的大小关系为( )
A. B. C. D.
A. B. C. D.
8.已知 的定义域为 ,且 是奇函数,当 时, ,函数
2.已知 ,则 ( )
,则方程 的所有的根之和为( )
A. B. C. D.
A.3 B.4 C.5 D.6
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
3.过抛物线 的焦点的直线的倾斜角为 ,则抛物线顶点到该直线的距离为( ) 要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
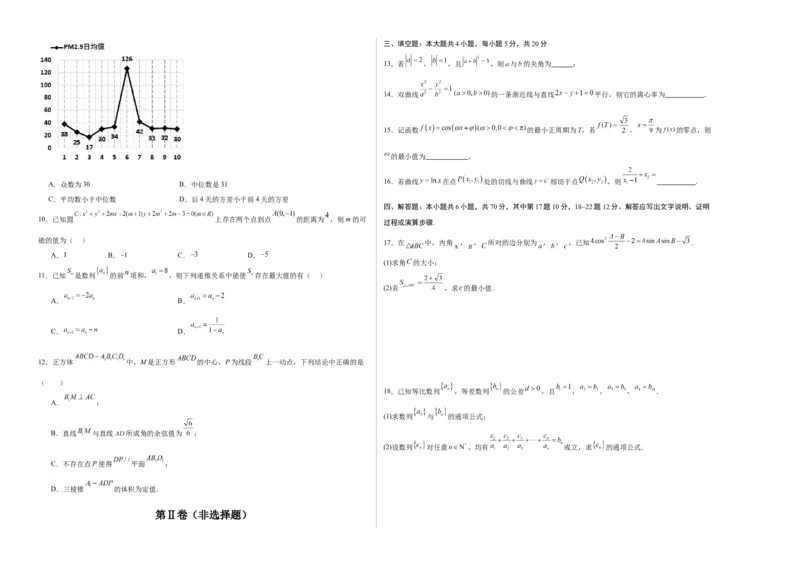
9.PM2.5是衡量空气质量的重要指标,下图是某地7月1日到10日的PM2.5日均值(单位: )的折线
A. B. C. D.1
图,则下列关于这10天中PM2.5日均值的说法正确的是( )
4.某校有1000人参加某次模拟考试,其中数学考试成绩近似服从正态分布N(105,σ2)(σ>0),试卷满分
150分,统计结果显示数学成绩优秀(高于120分)的人数占总人数的 ,则此次数学考试成绩在90分到
105分之间的人数约为( )
A.150 B.200 C.300 D.400
5.光岳楼,又称“余木楼”“鼓楼”“东昌楼”,位于山东省聊城市,在《中国名楼》站台票纪念册中,三、填空题:本大题共4小题,每小题5分,共20分
13.若 , ,且 ,则 与 的夹角为 ;
14.双曲线 的一条渐近线与直线 平行,则它的离心率为 .
15.记函数 的最小正周期为T,若 , 为 的零点,则
的最小值为 .
16.若曲线 在点 处的切线与曲线 相切于点 ,则 .
A.众数为30 B.中位数是31
C.平均数小于中位数 D.后4天的方差小于前4天的方差
四、解答题:本小题共6小题,共70分,其中第17题10分,18~22题12分。解答应写出文字说明、证明
10.已知圆 上存在两个点到点 的距离为 ,则m的可
过程或演算步骤.
能的值为( )
17.在 中,内角 , , 所对的边分别为 , , ,已知 .
A. B. C. D.
(1)求角 的大小;
11.已知 是数列 的前 项和, ,则下列递推关系中能使 存在最大值的有( )
(2)若 ,求 的最小值.
A. B.
C. D.
12.正方体 中,M是正方形 的中心,P为线段 上一动点,下列结论中正确的是
( )
18.已知等比数列 ,等差数列 的公差 ,且 , , , .
A. ;
(1)求数列 与 的通项公式;
B.直线 与直线 所成角的余弦值为 ;
(2)设数列 对任意 ,均有 成立,求 的通项公式.
C.不存在点P使得 平面 ;
D.三棱锥 的体积为定值.
第Ⅱ卷(非选择题)参考数据( )
19.如图,已知四边形 与 均为直角梯形,平面 平面EFAD, , ,
为 的中点, .
5215 17713 714 27 81.3 3.6
(3)根据以往每年平均气温以及对果园年产值的统计,得到以下数据:平均气温在22℃以下的年数占60%,
对柚子产量影响不大,不需要采取防虫措施;平均气温在22℃至28℃的年数占30%,柚子产量会下降
20%;平均气温在28℃以上的年数占10%,柚子产量会下降50%.为了更好的防治红蜘蛛虫害,农科所研发
出各种防害措施供果农选择.
在每年价格不变,无虫害的情况下,某果园年产值为200万元,根据以上数据,以得到最高收益(收益=产
(1)证明: , , , 四点共面;
值-防害费用)为目标,请为果农从以下几个方案中推荐最佳防害方案,并说明理由.
(2)求平面 与平面 夹角的余弦值.
方案1:选择防害措施A,可以防止各种气温的红蜘蛛虫害不减产,费用是18万;
方案2:选择防害措施B,可以防治22℃至28℃的蜘蛛虫害,但无法防治28℃以上的红蜘蛛虫害,费用是
10万;
方案3:不采取防虫害措施.
20.红蜘蛛是柚子的主要害虫之一,能对柚子树造成严重伤害,每只红蜘蛛的平均产卵数y(个)和平均温
度x(℃)有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值. 21.已知椭圆 的左、右顶点分别为 , ,点 为椭圆 上异于 , 的一点,且
直线 , 的斜率之积为 .
(1)求椭圆 的标准方程;
(2)直线 过右焦点 与椭圆 交于 , 两点( , 与 不重合), 不与 轴垂直,若
,求 .
(1)根据散点图判断, 与 (其中 …为自然对数的底数)哪一个更适合作为平均产卵
数y(个)关于平均温度x(℃)的回归方程类型?(给出判断即可,不必说明理由)
(2)由(1)的判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到0.1)
附:回归方程中 , ,
22.已知函数 .(1)若 ,求 在 上的最大值和最小值;
(2)讨论函数 的零点个数