文档内容
新题型 新高考新结构二十一大考点汇总
命题趋势
高考数学全国卷的考查内容、考查范围和考查要求层次与比例均与课程标准保持致注重考查内容的全面性的
同时,突出主干、重点内容的考查,通过依标施考,引导中学教学依标施教。
调整布局,打破固化模式。高考数学坚持稳中有变,通过调整试卷结构,改变相对固化的试题布局优化试题设
计,减少学生反复刷题、机械训练的收益,竭力破除复习备考中题海战术和题型套路,发挥引导作用。
热考题型解读
题型1 集合新考点
题型2 复数新考点
题型3 函数选图题新考点
题型4 比较大小新考点
题型5 数列小题新考点
题型6 排列组合小题新考点
题型7 圆锥曲线小题新考点
题型8 导数周期与对称新考点
题型9 抽象函数类新考点
题型10 函数导数新考点
题型11 不等式新考点
题型12 立体几何小题新考点
题型13 统计概率小题新考点
题型14 三角函数小题新考点
题型15 实际应用相关新考点
题型16 三角函数解答题新考点
题型17 立体几何解答题新考点
题型18 数列解答题新考点
题型19 统计概率解答题新考点
题型20 圆锥曲线解答题新考点
题型21 九省联考类19题
1【题型1集合新考点】
1 (2024·浙江温州·高三期末)设集合U=R,A= x2xx-2
2
<1 ,B=xy=ln(1-x) ,则图中阴影部分表
示的集合为 ( )
A.{x|x≥1} B.{x|1≤x<2} C.{x|00,则n的最小值为 ( )
A.1 B.3 C.6 D.9
【变式训练】
i2023
1 (多选)(2024上·云南·高三校联考阶段练习)若复数z= ,则 ( )
1-2i
2+i 5
A.z的共轭复数z= B.|z|=
5 5
1
C.复数z的虚部为- i D.复数z在复平面内对应的点在第四象限
5
2 (多选)(2024上·江西宜春·高三上高二中校考阶段练习)设z为复数,则下列命题中正确的是 ( )
A. z 2=zz B.若z=(1-2i)2,则复平面内z对应的点位于第二象限
C.z2=z 2 D.若z=1,则z+i的最大值为2
3 (多选)(2024上·云南德宏·高三统考期末)已知z是复数z的共轭复数,则下列说法正确的是 ( )
A.z⋅z=z2 B.若|z|=1,则z=±1
C.|z⋅z|=|z|⋅|z| D.若|z+1|=1,则|z-1|的最小值为1
1 3
4 (多选)(2024上·河南南阳·高三统考期末)设复数z=- - i的共轭复数为z,则下列结论正确的
2 2
有 ( )
2π 2π z 1
A.z=cos +isin B. =
3 3 z2 2
z
C. =1 D.z2+z2=2
z
【题型3函数选图题新考点】
1 (2024·浙江·高三期末)已知函数对任意的x∈R有f(x)+f(-x)=0,且当x>0时,f(x)=ln(x+1),则函
数f(x)的图象大致为 ( )
A. B.
C. D.
【变式训练】
5sinx
1 (2024·浙江宁波·高三期末)函数f(x)= +xcosx在[-2π,2π]上的图象大致为 ( )
e|x|
A. B.
3C. D.
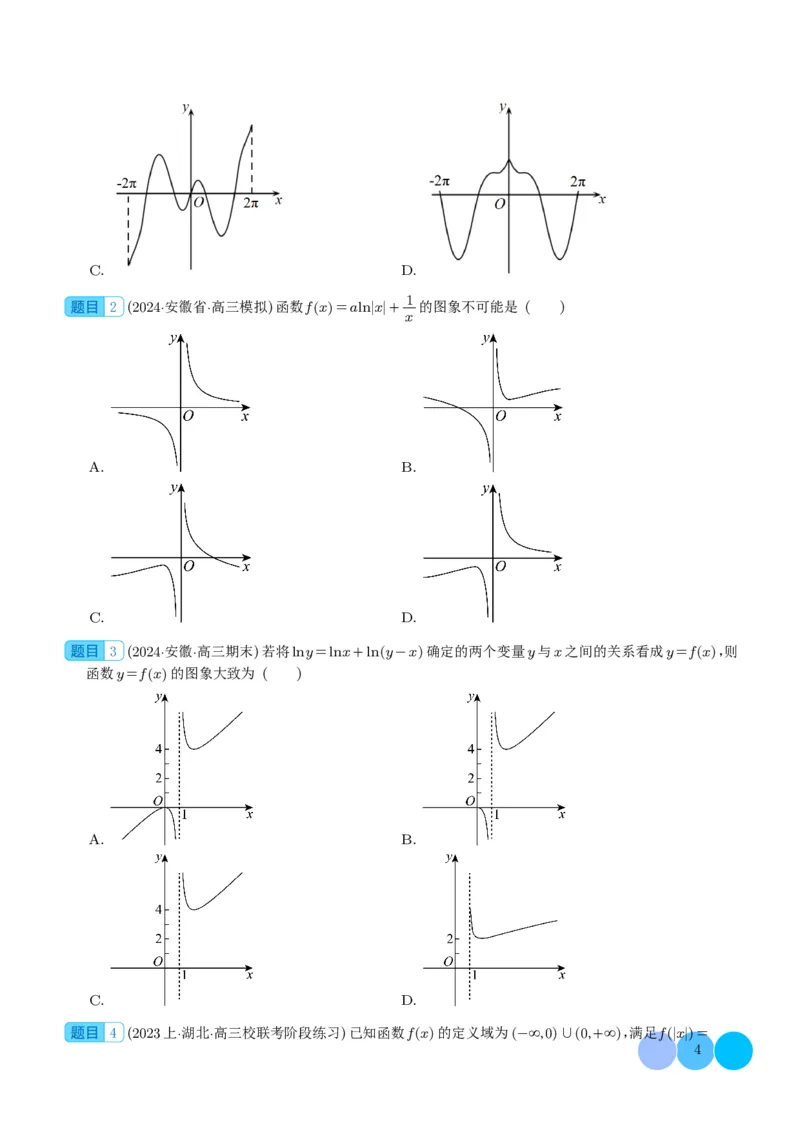
2 (2024·安徽省·高三模拟)函数fx
4
1
=alnx+ 的图象不可能是 ( )
x
A. B.
C. D.
3 (2024·安徽·高三期末)若将lny=lnx+lny-x 确定的两个变量y与x之间的关系看成y=fx ,则
函数y=fx 的图象大致为 ( )
A. B.
C. D.
4 (2023上·湖北·高三校联考阶段练习)已知函数fx 的定义域为-∞,0 ∪0,+∞ ,满足fx =fx
5
.当x<0时fx
1
= -x
x
lnx2,则fx 的大致图象为 ( )
A. B.
C. D.
【题型4比较大小新考点】
1
1 (2024·辽宁重点高中·模拟预测)设a=cos0.1,b=10sin0.1,c= ,则 ( )
10tan0.1
A.ab>c B.a>c>b C.c>a>b D.c>b>a
1
4 (2023·山东临沂·统考一模)已知x=
2
x
,log y= x,x=log z,则 ( )
1 x
2
A.xm>1,则 ( )
A3
A.C3=C5 B.C3= 7 C.mCm=(n-1)Cm-1 D.Am+mAm-1=Am
8 8 7 4! n n-1 n n n+1
【题型7 圆锥曲线小题新考点】
1 (2023上·上海浦东新·高三华师大二附中校考阶段练习)已知圆锥曲线Γ:fx,y =1关于坐标原点O对
称,定点P的坐标为x 0 ,y 0 .给出两个命题:①若00 ,M是抛物线C上的动
1
点,焦点F ,0
2
,N4,2 ,下列说法正确的是 ( )A.C的方程为y2=x B.C的方程为y2=2x
5 9
C. MF+MN的最小值为 D. MF+MN的最小值为
2 2
3 (2024江西九师联盟)阿波罗尼斯(约公元前262年~约公元前190年),古希腊著名数学家,主要著作
有《圆锥曲线论》、《论切触》等,尤其《圆锥曲线论》是一部经典巨著,代表了希腊几何的最高水平,此书集前人
之大成,进一步提出了许多新的性质,其中也包括圆锥曲线的光学性质,光线从双曲线的一个焦点发出,通过
x2 y2
双曲线的反射,反射光线的反向延长线经过其另一个焦点,已知双曲线C: - =1a>0,b>0的左、右
a2 b2
焦点分别为F,F,其离心率为e= 5,从F 发出的光线经过双曲线C的右支上一点E的反射,反射光线为
1 2 2
EP,若反射光线与入射光线垂直,则sin∠FFE=
2 1
5 5 4 2 5
A. B. C. D.
6 5 5 5
4 (2024·浙江宁波·高三期末)(多选)已知O为坐标原点,曲线Γ:x2+y2
8
2=ay3x2-y2 ,a>0,
Px 0 ,y 0 为曲线Γ上动点,则 ( )
A.曲线Γ关于y轴对称 B.曲线Γ的图象具有3条对称轴
C.y ∈ -a, 9 a
0 16
D. OP的最大值为 3a
【题型8 导数周期与对称新考点】
1 (2024·陕西西安·统考一模)已知函数f(x)及其导函数f(x)的定义域均为R,记g(x)=f(x),若f(1-2x)
1
+4x为偶函数,g(x+2)=g(x-4),且g-
2
5
=0,则g
2
+g(4)= ( )
A.4 B.6 C.8 D.10
【变式训练】
1 (2023上·四川·高三校联考阶段练习)已知函数fx 及其导函数f x 的定义域均为R,且fx-1 为
奇函数,f 2-x +f x =-2,f -1
27
=-2,则f 2i-1
i=1
= ( )
A.-28 B.-26 C.-24 D.-22
2 (2024上·浙江宁波·高三统考期末)已知函数fx 的定义域为R,且fx+y fx fy =fx+y -
fx -fy ,f1
2024
= 3,则 fk
k=1
= ( )
A.2024 B.1012 3 C. 3 D.0
3 (2024上·山东淄博·高三统考期末)已知函数fx ,gx 的定义域都为R,g x 为gx 的导函数,g
x 的定义域也为R,且fx +g x =2,fx -g 4-x =2,若gx 为偶函数,则下列结论中一定成立的
个数为 ( )
①f4 =2 ②g 2 =0 ③f1 =f3 ④f-1 +f-3 =4A.1 B.2 C.3 D.4
4 (多选)(2024上·河南漯河·高三统考期末)已知函数f(x)及其导函数f'(x)的定义域均为R,若函数y
1
=f(3-2x)为奇函数,函数y= x-f(x+2)为偶函数,g(x)=f'(x),则 ( )
3
2 1 2 2
A. g(0)= B. g(4)= C. g(0)+g(2)= D. g(4)-g(6)=
3 3 3 3
【题型9 抽象函数类新考点】
1【2024九省联考第11题】已知函数 fx
9
1
的定义域为R,且 f
2
≠0,若 fx+y + fx fy =4xy,则
( )
1
A. f-
2
1
=0 B. f
2
=-2
1
C.函数fx-
2
1
是偶函数 D.函数fx+
2
是减函数
【变式训练】
22
1 (2022•新高考Ⅱ)已知函数f(x)的定义域为R,且f(x+y)+f(x-y)=f(x)f(y),f(1)=1,则f(k)
k=1
= ( )
A.-3 B.-2 C.0 D.1
2 (2023•玉林三模)函数fx 对任意x,y∈R总有fx+y =fx +fy ,当x<0时,fx <0,f1
1
= ,则下列命题中正确的是 ( )
3
A. fx 是偶函数
B. fx 是R上的减函数
C. fx 在-6,6 上的最小值为-2
D.若fx +fx-3 ≥-1,则实数x的取值范围为3,+∞
3 已知函数fx 的定义域D为-∞,0 ∪0,+∞ ,fx 在-∞,0 上单调递减,且对任意的x,x ∈D, 1 2
都有fx 1 x 2 =fx 1 +fx 2 -1,若对任意的x∈1,+∞ ,不等式fax -flnx >f1 -1恒成立,则实数
a的取值范围是 .
4 (2024· 江苏南通·高三模拟)(多选)已知函数fx 的定义域为R,且fx+y fx-y =f2 x -f2 y ,
f1
3
= 3,f2x+
2
为偶函数,则 ( )
A. f(0)=0 B. fx 为偶函数
2023
C. f(3+x)=-f(3-x) D.f(k)= 3
k=1
【题型10函数导数新考点】
1 (多选)(2022·山东菏泽·统考一模)对圆周率π的计算几乎贯穿了整个数学史.古希腊数学家阿基米德(公
22
元前287-公元前212)借助正96边形得到著名的近似值: .我国数学家祖冲之(430-501)得出近似
7
355 355
值 ,后来人们发现π- <10-6,这是一个“令人吃惊的好结果” .随着科技的发展,计算π的方法
113 113
越来越多.已知π=3.141592653589793238462643383279502⋯,定义fn n∈N 的值为π的小数点后第
n个位置上的数字,如f1 =1,f4 =5,规定f0 =3.记f1 n =fn ,fk+1 n =fk fn k∈N* ,集合A 为函数fk n
k
10
n∈N 的值域,则以下结论正确的有 ( )
A.A=0,1,2,3,4,5,6,7,8,9
1
B.A =1,2,3,4,5,6,9
3
C.对∀k∈N*,1∈A D.对∀k∈N*,A 中至少有两个元素
k k
【变式训练】
1 (2024·高三·期末)(多选)在平面直角坐标系中,将函数f(x)的图象绕坐标原点逆时针旋转α (0<α≤
90°)后,所得曲线仍然是某个函数的图象,则称f(x)为“α旋转函数”.那么 ( )
A.存在90°旋转函数 B.80°旋转函数一定是70°旋转函数
1 bx
C.若g(x)=ax+ 为45°旋转函数,则a=1 D.若h(x)= 为45°旋转函数,则-e2≤b≤0
x ex
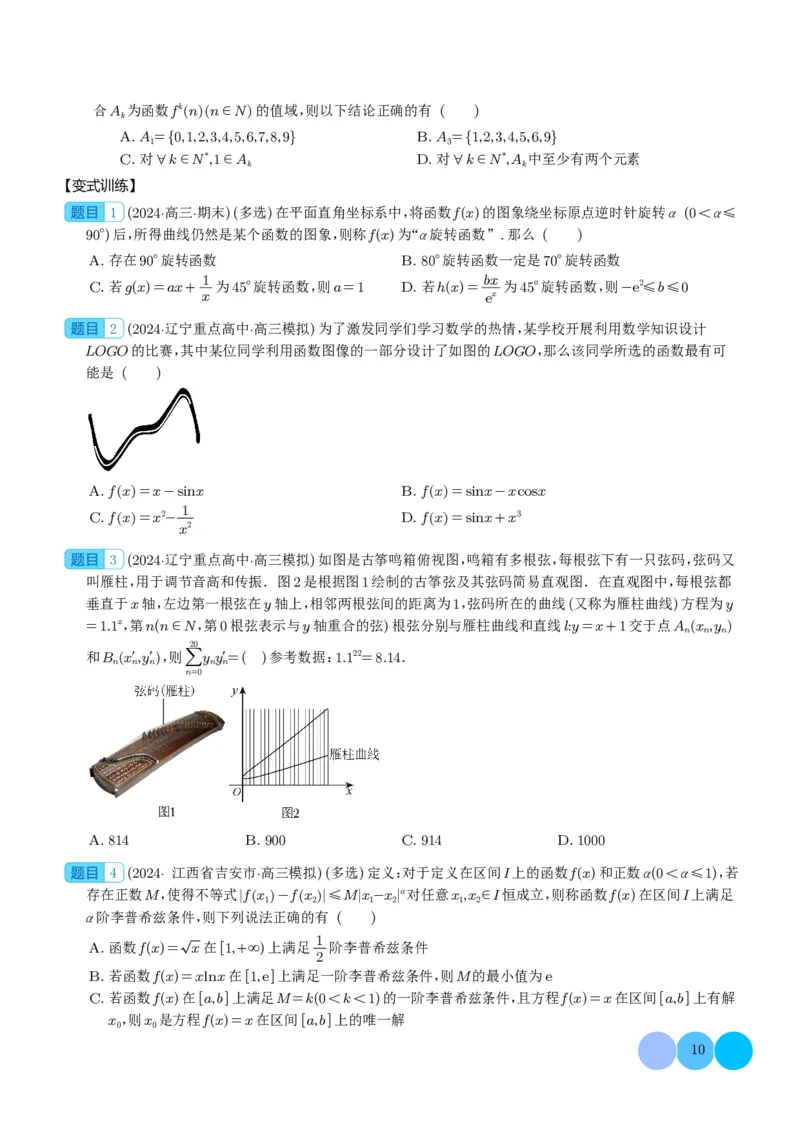
2 (2024·辽宁重点高中·高三模拟)为了激发同学们学习数学的热情,某学校开展利用数学知识设计
LOGO的比赛,其中某位同学利用函数图像的一部分设计了如图的LOGO,那么该同学所选的函数最有可
能是 ( )
A. fx =x-sinx B. fx =sinx-xcosx
C. fx
1
=x2- D. fx
x2
=sinx+x3
3 (2024·辽宁重点高中·高三模拟)如图是古筝鸣箱俯视图,鸣箱有多根弦,每根弦下有一只弦码,弦码又
叫雁柱,用于调节音高和传振.图2是根据图1绘制的古筝弦及其弦码简易直观图.在直观图中,每根弦都
垂直于x轴,左边第一根弦在y轴上,相邻两根弦间的距离为1,弦码所在的曲线(又称为雁柱曲线)方程为y
=1.1x,第n(n∈N,第0根弦表示与y轴重合的弦)根弦分别与雁柱曲线和直线l:y=x+1交于点A nx n ,y n
和B nx n ,y n
20
,则y y=( )参考数据:1.122=8.14. n n
n=0
A.814 B.900 C.914 D.1000
4 (2024· 江西省吉安市·高三模拟)(多选)定义:对于定义在区间I上的函数f(x)和正数α(0<α≤1),若
存在正数M,使得不等式 fx 1 -fx 2 ≤Mx 1 -x 2 α对任意x 1 ,x 2 ∈I恒成立,则称函数f(x)在区间I上满足
α阶李普希兹条件,则下列说法正确的有 ( )
1
A.函数f(x)= x在[1,+∞)上满足 阶李普希兹条件
2
B.若函数f(x)=xlnx在[1,e]上满足一阶李普希兹条件,则M的最小值为e
C.若函数f(x)在[a,b]上满足M=k(00,则A=maxx, 1
y
2 +maxy,
x
的最小值为 ;B=maxx, 1
y
2 +maxy,
z
3 +maxz,
x
的最小值为 .
【变式训练】
1 【2024九省联考】以max M表示数集M中最大的数.设0 ,y>3,不等式k2x-3
2
y-3 ≤8x3+y3-12x2
-3y2恒成立,则实数k的最大值为 ( )
A.12 B.24 C.2 3 D.4 3
1 2 4
3 (2018·河南·高三竞赛)已知a、b、c均为正数,则min , , ,3abc
a b c
的最大值为 .
4 (2018·全国·高三竞赛)设非负实数x、y、z满足x+y+z=1.则t= 9+x2+ 4+y2+ 1+z2的最
小值为 .
5 (2023·全国·高三专题练习)设fx,y,z
x2y-z
=
y2z-x
+
1+x+3y
z2x-y
+
1+y+3z
,其中x、y、z≥0 ,
1+z+3x
且x+y+z=1.求fx,y,z 的最大值和最小值.【题型12立体几何小题新考点】
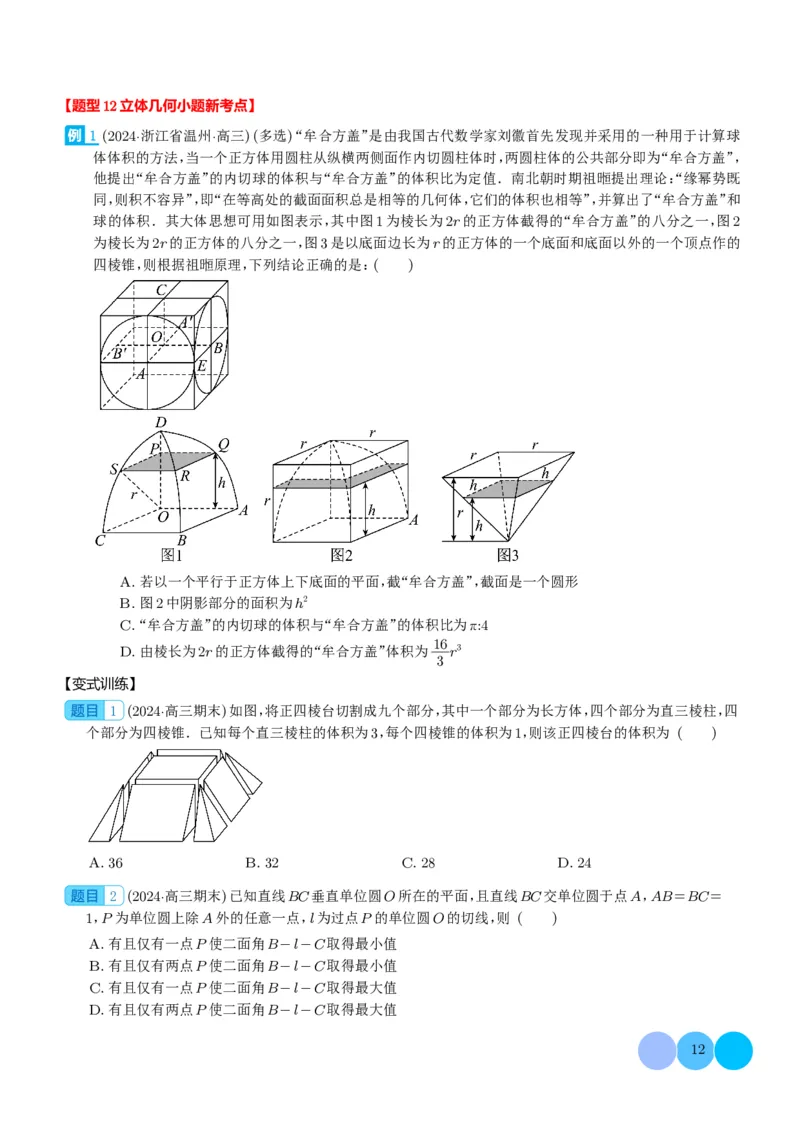
1 (2024·浙江省温州·高三)(多选)“牟合方盖”是由我国古代数学家刘徽首先发现并采用的一种用于计算球
体体积的方法,当一个正方体用圆柱从纵横两侧面作内切圆柱体时,两圆柱体的公共部分即为“牟合方盖”,
他提出“牟合方盖”的内切球的体积与“牟合方盖”的体积比为定值.南北朝时期祖暅提出理论:“缘幂势既
同,则积不容异”,即“在等高处的截面面积总是相等的几何体,它们的体积也相等”,并算出了“牟合方盖”和
球的体积.其大体思想可用如图表示,其中图1为棱长为2r的正方体截得的“牟合方盖”的八分之一,图2
为棱长为2r的正方体的八分之一,图3是以底面边长为r的正方体的一个底面和底面以外的一个顶点作的
四棱锥,则根据祖暅原理,下列结论正确的是:( )
A.若以一个平行于正方体上下底面的平面,截“牟合方盖”,截面是一个圆形
B.图2中阴影部分的面积为h2
C.“牟合方盖”的内切球的体积与“牟合方盖”的体积比为π:4
16
D.由棱长为2r的正方体截得的“牟合方盖”体积为 r3
3
【变式训练】
1 (2024·高三期末)如图,将正四棱台切割成九个部分,其中一个部分为长方体,四个部分为直三棱柱,四
个部分为四棱锥.已知每个直三棱柱的体积为3,每个四棱锥的体积为1,则该正四棱台的体积为 ( )
A.36 B.32 C.28 D.24
2 (2024·高三期末)已知直线BC垂直单位圆O所在的平面,且直线BC交单位圆于点A,AB=BC=
1,P为单位圆上除A外的任意一点,l为过点P的单位圆O的切线,则 ( )
A.有且仅有一点P使二面角B-l-C取得最小值
B.有且仅有两点P使二面角B-l-C取得最小值
C.有且仅有一点P使二面角B-l-C取得最大值
D.有且仅有两点P使二面角B-l-C取得最大值
123 (2024·辽宁重点高中·高三模拟)表面积为4π的球内切于圆锥,则该圆锥的表面积的最小值为 ( )
A.4π B.8π C.12π D.16π
4 (2024·辽宁重点高中·高三模拟)(多选)在空间直角坐标系中,有以下两条公认事实:
(1)过点P 0x 0 ,y 0 ,z 0
13
,且以u=a,b,c abc≠0
x-x y-y
为方向向量的空间直线l的方程为 0 = 0 = a b
z-z
0;
c
(2)过点Px 0 ,y 0 ,z 0
,且v=m,n,t mnt≠0 为法向量的平面α的方程为mx-x 0 +ny-y 0 +
tz-z 0 =0.
现已知平面α:x+2y+3z=6,l 1 : 2 3 x y- - 2 y z = = 1 1 ,l 2 :x=y=2-z,l 3 : x- 5 1 = - y 4 = z 1 ( )
A.l⎳α B.l ⎳α C.l ⎳α D.l⊥α
1 2 3 1
【题型13统计概率小题新考点】
1 (2024·浙江省温州)在研究急刹车的停车距离问题时,通常假定停车距离等于反应距离(d ,单位:m)与制
1
动距离(d ,单位:m)之和.如图为某实验所测得的数据,其中“KPH”表示刹车时汽车的初速度v(单位:
2
km/h).根据实验数据可以推测,下面四组函数中最适合描述d ,d 与v的函数关系的是 ( )
1 2
A.d=αv,d =β v B.d=αv,d =βv2 C.d=α v,d =βv D.d=α v,d =βv2
1 2 1 2 1 2 1 2
【变式训练】
1 (2024·河北省·高三模拟)现有甲、乙两组数据,每组数据均由六个数组成,其中甲组数据的平均数为3,
方差为5,乙组数据的平均数为5,方差为3.若将这两组数据混合成一组,则新的一组数据的方差为 ( )
A.3.5 B.4 C.4.5 D.5
2 (2022下·山西运城·高二校联考阶段练习)已知n为满足T=a+C 2 1 022 +C 2 2 022 +C 2 3 022 +⋯+C 2 2 0 0 2 2 2 2 a≥3
能被9整除的正整数a的最小值,则x2-x+2 x-1 n的展开式中含x10的项的系数为 .
3 (2022·贵州·高二统考竞赛)如图,“爱心”是由曲线C:x2+y2=2|y|(x≤0)和C :|y|=cosx+1(0≤x≤
1 2
-1≤x≤π
π)所围成的封闭图形,在区域Ω= (x,y)
-2≤y≤2
内任取一点A,则A取自“爱心”内的概率P=
.4 (2018·全国·高三竞赛)设n为正整数.从集合1,2,⋯,2015
14
中任取一个正整数n恰为方程 n
2
=
n
3
+ n
6
的解的概率为 (x 表示不超过实数x的最大整数).
【题型14三角函数小题新考点】
1 (2024浙江省温州高三)已知函数fx =asin2x+bcos2xab≠0
π
的图象关于直线x= 对称,若存在
6
x 1 ,x 2 ,⋯,x n ,满足 fx 1 -fx 2 + fx 2 -fx 3 +⋯+ fx n-1 -fx n =24b,其中n≥2,n∈N + ,则n的
最小值为 ( )
A.6 B.7 C.8 D.9
【变式训练】
1 (2024·辽宁重点高中·高三模拟)(多选)已知对任意角α,β均有公式sin2α+sin2β=
2sinα+β cosα-β .设△ABC的内角A,B,C满足sin2A+sinA-B+C =sinC-A-B
1
+ .面
2
积S满足1≤S≤2.记a,b,c分别为A,B,C所对的边,则下列式子一定成立的是 ( )
1 a
A.sinAsinBsinC= B.2≤ ≤2 2
4 sinA
C.8≤abc≤16 2 D.bcb+c >8
2 (2024· 江苏南通·高三模拟)(多选)若函数fx =2sin2x⋅log sinx+2cos2x⋅log cosx,则 ( ) 2 2
A. fx 的最小正周期为π B. fx
π
的图像关于直线x= 对称
4
C. fx 的最小值为-1 D. fx
π
的单调递减区间为2kπ, +2kπ
4
,k∈Z
3 8
3 (2024· 江苏南通·高三模拟)函数f(x)= + (x∈R)的最小值 .
2sin2x+1 3cos2x+2
4 (2024·河北省·高三模拟)蚊香具有悠久的历史,我国蚊香的发明与古人端午节的习俗有关.如图为某
校数学社团用数学软件制作的“蚊香”. 画法如下:在水平直线上取长度为1的线段AB,作一个等边三角形
ABC,然后以点B为圆心,AB为半径逆时针画圆弧交线段CB的延长线于点D(第一段圆弧),再以点C为圆
心,CD为半径逆时针画圆弧交线段AC的延长线于点E,再以点A为圆心,AE为半径逆时针画圆弧⋯⋯
以此类推,当得到的“蚊香”恰好有15段圆弧时,“蚊香”的长度为 ( )A.44π B.64π C.70π D.80π
5 (2024·浙江·高三期末)已知0 3 C.x+x <2x D.x+x >2x
x x x x 1 3 2 1 3 2
1 3 1 3
【题型15实际应用相关新考点】
1 (2024·浙江温州·高三)著名数学家、物理学家牛顿曾提出:物体在空气中冷却,如果物体的初始温度为
θ 1 °C,空气温度为θ 0 °C,则t分钟后物体的温度θ(单位:°C)满足:θ=θ 0 +θ 1 -θ 0 e-kt.若常数k=0.05,空
气温度为30°C,某物体的温度从90°C下降到50°C,大约需要的时间为( )(参考数据:ln3≈1.1)
A.16分钟 B.18分钟 C.20分钟 D.22分钟
【变式训练】
1 (2024上·河南·高三校联考期末)据科学研究表明,某种玫瑰花新鲜程度y与其花朵凋零时间t(分钟)
(在植物学上t表示从花朵完全绽放时刻开始到完全凋零时刻为止所需的时间)近似满足函数关系式:y=b⋅
t 1 1
210(b为常数),若该种玫瑰花在凋零时间为10分钟时的新鲜程度为 ,则当该种玫瑰花新鲜程度为 时,
10 2
其凋零时间约为(参考数据:lg2≈0.3) ( )
A.3分钟 B.30分钟 C.33分钟 D.35分钟
2 (2024上·北京房山·高三统考期末)保护环境功在当代,利在千秋,良好的生态环境既是自然财富,也是
经济财富,关系社会发展的潜力和后劲.某工厂将生产产生的废气经过过滤后排放,已知过滤过程中的污染
物的残留数量P(单位:毫米/升)与过滤时间t(单位:小时)之间的函数关系为P=P⋅e-kt(t≥0),其中k为常
0
数,k>0,P为原污染物数量.该工厂某次过滤废气时,若前9个小时废气中的污染物恰好被过滤掉80%,那
0
1
么再继续过滤3小时,废气中污染物的残留量约为原污染物的(参考数据:
5
1
3≈0.585) ( )
A.12% B.10% C.9% D.6%
3 (2023上·宁夏银川·高三宁夏育才中学校考阶段练习)“开车不喝酒,喝酒不开车.”,饮酒驾驶和醉酒驾
驶都是根据驾驶人员血液、呼气酒精含量来确定,经过反复试验,一般情况下,某人喝一瓶啤酒后血液中的酒
精含量值fx 随着时间x(小时)的变化规律,可以用函数模型fx
π
40sin x
= 3
+13, 0≤x<2
来拟
90⋅e-0.5x+14, x≥2
合,则该人喝一瓶啤酒至少经过多少小时后才可以驾车?( )(参考数据:ln15≈2.71,ln30≈3.40)
驾驶行为类别 酒精含量值(mg/100mL)
饮酒驾驶 ≥20,<80
醉酒驾驶 ≥80
A.5 B.6 C.7 D.84 (2024·山东青岛·高三期末)1551年奥地利数学家、天文学家雷蒂库斯在《三角学准则》中首次用直角三
角形的边长之比定义正割和余割,在某直角三角形中,一个锐角的斜边与其邻边的比,叫做该锐角的正割,用
sec(角)表示;锐角的斜边与其对边的比,叫做该锐角的余割,用csc(角)表示,则csc10°- 3sec10°= ( )
A. 3 B.2 3 C.4 D.8
【题型16三角函数解答题新考点】
π
1 (2024·高三·期末)设02;
x-sinx
(3)若tanx+2sinx-ax>0,求实数a的取值范围.
【变式训练】
1 (2024·河北省·高三模拟)已知定义域为R的函数hx
16
满足:对于任意的x∈R,都有hx+2π =hx
+h2π ,则称函数hx 具有性质P.
(1)判断函数fx =2x,gx =cosx是否具有性质P;(直接写出结论)
(2)已知函数fx =sinωx+φ
3 5 π
<ω< ,φ<
2 2 2
,判断是否存在ω,φ,使函数fx 具有性质P?若存
在,求出ω,φ的值;若不存在,说明理由;
(3)设函数fx 具有性质P,且在区间0,2π 上的值域为 f0 ,f2π .函数gx =sin fx ,满足
gx+2π =gx ,且在区间0,2π 上有且只有一个零点.求证:f2π =2π.2 (2024·安徽省·高三模拟)在△ABC中,角A,B,C的对边分别为a,b,c,sin2B+sin2C=sin2A+
sinBsinC.
(1)若△ABC的面积S=2 3,b+c=6,求a的值;
(2)若函数fx
17
lnx
=3x2-4x- +1在区间0,t
cosA
上有零点,求t的取值范围.
π
3 (浙江省杭州第二中学2021-2022学年高三上学期调研考试数学试题)在△ABC中,∠B= ,D为
2
BD AB+AD
BC边上一点且 = .
CD AC+AD
(1)证明:△ABD和△ADC的内切圆半径相等;
(2)若△ABC的三边长构成等差数列,求∠ADB的大小.4 (2021·上海普陀·统考二模)如图所示,某人为“花博会”设计一个平行四边形园地,其顶点分别为A(i
i
=1,2,3,4),AA =30米,∠A AA =120°,D为对角线A A 和AA 的交点.他以A 、A 为圆心分别画圆
1 2 2 1 4 2 4 1 3 2 4
弧,一段弧与AA 相交于A 、另一段弧与A A 相交于A ,这两段弧恰与A A 均相交于D.设∠AA D=θ.
1 2 1 3 4 3 2 4 1 2
(1)若两段圆弧组成“甬路”L(宽度忽略不计),求L的长(结果精确到1米);
L S
(2)记此园地两个扇形面积之和为S ,其余区域的面积为S .对于条件(1)中的L,当 - 1<0.12
1 2 AA S
1 3 2
时,则称其设计“用心”,问此人的设计是否“用心”?并说明理由.
【题型17立体几何解答题新考点】
1 (2024·江西省九师联盟)如图,在△ABC中,AB=BC=2,D为△ABC外一点,AD=2CD=4,记
∠BAD=α,∠BCD=β.
(1)求2cosα-cosβ的值;
(2)若△ABD的面积为S ,△BCD的面积为S ,求S2+S2的最大值.
1 2 1 2
18【变式训练】
1 (2024·浙江温州·高三)某数学建模小组研究挡雨棚(图1),将它抽象为柱体(图2),底面ABC与AB
1 1
C 全等且所在平面平行,△ABC与△ABC 各边表示挡雨棚支架,支架AA 、BB 、CC 垂直于平面ABC.雨
1 1 1 1 1 1 1
π π
滴下落方向与外墙(所在平面)所成角为 (即∠AOB= ),挡雨棚有效遮挡的区域为矩形AAOO(O、O
6 6 1 1 1
分别在CA、CA 延长线上).
1 1
(1)挡雨板(曲面BBCC)的面积可以视为曲线段BC与线段BB 长的乘积.已知OA=1.5米,AC=0.3
1 1 1
π
米,AA=2米,小组成员对曲线段BC有两种假设,分别为:①其为直线段且∠ACB= ;②其为以O为圆
1 3
心的圆弧.请分别计算这两种假设下挡雨板的面积(精确到0.1平方米);
π π
(2)小组拟自制△ABC部分的支架用于测试(图3),其中AC=0.6米,∠ABC= ,∠CAB=θ,其中 <θ
2 6
π
< ,求有效遮挡区域高OA的最大值.
2
192 (2024·浙江·高三期末)如图,以AD所在直线为轴将直角梯形ABCD旋转得到三棱台ABE-DCF,
其中AB⊥BC,AB=2BC=2CD.
(1)求证:AD⊥BE;
π
(2)若∠EAB= ,求直线AD与平面CDF所成角的正弦值.
3
3 (2024·辽宁重点高中·高三模拟)如图,在直三棱柱ABC-ABC 中,AB=AC,点D在棱AA 上,且
1 1 1 1
1
AD= AA,E为AC 的中点.
1 3 1 1 1
(1)证明:平面BDE⊥平面BCCB ;
1 1
(2)若AB=AA=2,BC=2 2,求二面角D-BE-A 的余弦值.
1 1
204 (2024· 江西省吉安市·高三模拟)如图,在正三棱锥P-ABC中,有一半径为1的半球,其底面圆O与
正三棱锥的底面贴合,正三棱锥的三个侧面都和半球相切.设点D为BC的中点,∠ADP=α.
(1)用α分别表示线段BC和PD长度;
π
(2)当α∈0,
2
21
时,求三棱锥的侧面积S的最小值.
【题型18数列解答题新考点】
1 (2024·辽宁重点高中·高三模拟) 记 S 为数列 a
n n
的前 n 项和,且满足 S = kna +pa +qn +
n n n
rk,p,q,r∈R .
1
(1)若p=r=0,k= ,求证:数列a
2 n
是等差数列;
(2)若k=q=0,p=2,r≠0,设b n =-1
S
n+1 n,数列b r n 的前n项和为T,若对任意的k∈N*,都有T < n 2k-1
λk
n m k
22
,必有a
m+1
-a =t”,则称数列{a }具有P(t)性质.
k+1 n
2n (n=1,2)
(1)若数列{a }满足a = n n 2n-5 n≥3,n∈N*
,判断数列{a n }是否具有P(1)性质?是否具有P(4)性
质?
(2)对于无穷数列{a },设T={x|x=a-a,i0)元,若试验成功则获利8a元,则该公司应
如何决策投资?请说明理由.3 (2024·安徽省·高三模拟)同余定理是数论中的重要内容.同余的定义为:设a,b∈Z,m∈N*且m>
1.若m(a-b)则称a与b关于模m同余,记作a≡b(modm)(“|”为整除符号).
(1)解同余方程x2-x≡0(mod3);
(2)设(1)中方程的所有正根构成数列a
n
23
,其中a0,y >0,k=1,2,⋯,n,x =y =1.指标D(X‖Y)可用来刻画X和Y的相似
k k k k k
k=1 k=1
n x
程度,其定义为D(X‖Y)=x ln k.设X~B(n,p),0b>0)上一点x 0 ,y 0 处的切线方程为 ?
x2
(3)P(m,n)是椭圆L: +y2=1外一点,过点P作椭圆的两条切线,切点分别为A,B,如图,则直线AB的方
3
程是 ?这是因为在Ax 1 ,y 1 ,Bx 2 ,y 2
xx x x
两点处,椭圆L的切线方程为 1 +y y=1和 2 +y y=1.两切 3 1 3 2
xm x m
线都过P点,所以得到了 1 +yn=1和 2 +y n=1,由这两个“同构方程”得到了直线AB的方程;
3 1 3 2
(4) 问题 (3) 中两切线 PA,PB 斜率都存在时,设它们方程的统一表达式为 y - n = k(x - m),由
y-n=k(x-m)
x2+3y2=3
,得(1+3k2)x2+6k(n-km)x+3(n-km)2-3=0,化简得Δ=0,得(3-m2)k2+2mnk+
1-n2=0.若PA⊥PB,则由这个方程可知P点一定在一个圆上,这个圆的方程为 ?2 (2023·安徽·统考一模)我们约定,如果一个椭圆的长轴和短轴分别是另一条双曲线的实轴和虚轴,则
x2 y2
称它们互为“姊妹”圆锥曲线.已知椭圆C 1 : 4 + b2 =100,b>0)的左、右焦点分别为F、F,离心率
a2 b2 1 2
1 π
为 ,经过点F且倾斜角为θ0<θ<
2 1 2
29
的直线l与椭圆交于A、B两点(其中点A在x轴上方),△ABF 的
2
周长为8.
(1)求椭圆C的标准方程;
(2)如图,将平面xOy沿x轴折叠,使y轴正半轴和x轴所确定的半平面(平面AFF)与y轴负半轴和x轴所
1 2
确定的半平面(平面BFF)互相垂直.
1 2
π
①若θ= ,求三棱锥A-BFF 的体积,
3 1 2
π
②若θ= ,异面直线AF和BF 所成角的余弦值;
3 1 2
π
③是否存在θ0<θ<
2
15
,使得△ABF 折叠后的周长为与折叠前的周长之比为 ?若存在,求tanθ的值;
2 16
若不存在,请说明理由.x2 y2 x2+4x y2
4 (2024·高三·期末)已知椭圆C: + =1的左焦点为F,P为曲线E: + =0上的动点,
25 9 25 9
且点P不在x轴上,直线FP交C于A,B两点.
(1)证明:曲线E为椭圆,并求其离心率;
(2)证明:P为线段AB的中点;
(3)设过点A,B且与AB垂直的直线与C的另一个交点分别为M,N,求△PMN面积的取值范围.
【题型21九省联考类19题】
a a
1 (2024·浙江温州·高三)设数阵A = 11 12
0 a a
21 22
30
,其中a ,a ,a ,a ∈1,2,3,4,5,6
11 12 21 22
.设S=e,e ,⋯,e
1 2 l
⊆
1,2,3,4,5,6 ,其中e