文档内容
2024 届高三第二学期期初学业质量监测
数学
注意事项:
考生在答题前请认真阅读本注意事项及各题答题要求
1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷
上无效.
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一项是
符合题目要求的。
1.已知样本数据1,2,2,3,7,9,则2.5是该组数据的( )
A.极差 B.众数 C.平均数 D.中位数
2.3名男生和2名女生站成一排.若男生不相邻,则不同排法种数为( )
A.6 B.12 C.24 D.72
3.设a∈R.若函数 f(x)=(a−1)x为指数函数,且 f(2)> f(3),则a的取值范围是( )
A.12b”是“sin A>sin2B”的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
x2 y2
7.已知双曲线C: − =1(a >0,b>0)的左、右焦点分别为F,F ,点P在C的左支上,∠PFF =60°,
a2 b2 1 2 1 2
△PFF 的周长为6a,则C的离心率为( )
1 2
A.2 B. 3 C. 2 D. 5−1
a
8.已知正五边形的边长为a,内切圆的半径为r,外接圆的半径为R,R+r = ,则θ=( )
2tanθ
A.9° B.18° C.27° D.36°
二、选择题:本题共 3小题,每小题 6分,共 18分。在每小题给出的选项中,有多项符合题目
学学科科网网((北北京京))股股份份有有限限公公司司要求。全部选对的得 6分,部分选对的得 3分,有选错的得 0分。
9.已知函数 f(x)=cos2x+2sinx,则( )
π
A. f(x)的最小正周期为2π B. f(x)关于直线x= 对称
2
π
C. f(x)关于点 ,0 中心对称 D. f(x)的最小值为−3
2
10.在平面直角坐标系xOy中,已知抛物线C: y2 =4x的焦点为F,准线l与x轴的交点为A,点M,N在C
上,且FM +FA=2FN ,则( )
2 2
A.ON∥FM B.直线MN的斜率为±
3
17 AF⋅AM
C.|MN |= D. =2 2
2 | AM |
11.已知函数 f(x)及其导函数g(x的定义域均为R, f(2x+1)与g(2x−1)均为偶函数,则( )
9
A. f(−1)=0 B. f(x+8)= f(x) C.g(3)=0 D.∑g(k)=0
k=1
三、填空题:本题共 3小题,每小题 5分,共 15分.
{ ( ) ( ) }
12.设m∈R,i为虚数单位.若集合M = 1,2, m2 +3m−1 + m2 +5m−6 i ,N ={−1,3},且M N ={3},
则m=__________.
13.一个三棱锥形木料P−ABC ,其中△ABC是边长为2dm的等边三角形,PA⊥底面ABC,二面角
P−BC−A的大小为45°,则点A到平面PBC的距离为__________dm.若将木料削成以A为顶点的圆锥,
且圆锥的底面在侧面PBC内,则圆锥体积的最大值为_________dm3.
14.已知a,b,c为某三角形的三边长,其中aa+b−c恒成立,则M的最小值为__________.
四、解答题:本题共 5小题、共 77分。解答应写出文字说明、证明过程成演算步骤。
15.(13分)
2
假定某同学每次投篮命中的概率为 ,
3
(1)若该同学投篮4次,求恰好投中2次的概率;
(2)该同学现有4次投篮机会,若连续投中2次,即停止投篮,否则投篮4次,求投篮次数X的概率分布及
数学期望.
16、(15分)
学学科科网网((北北京京))股股份份有有限限公公司司己知函数 f(x)=alnx−x+1,其中a∈R.
(1)若曲线y = f(x)在x=1处的切线在两坐标轴上的截距相等,求a;
(2)求函数 f(x)的单调区间.
17.(15分)
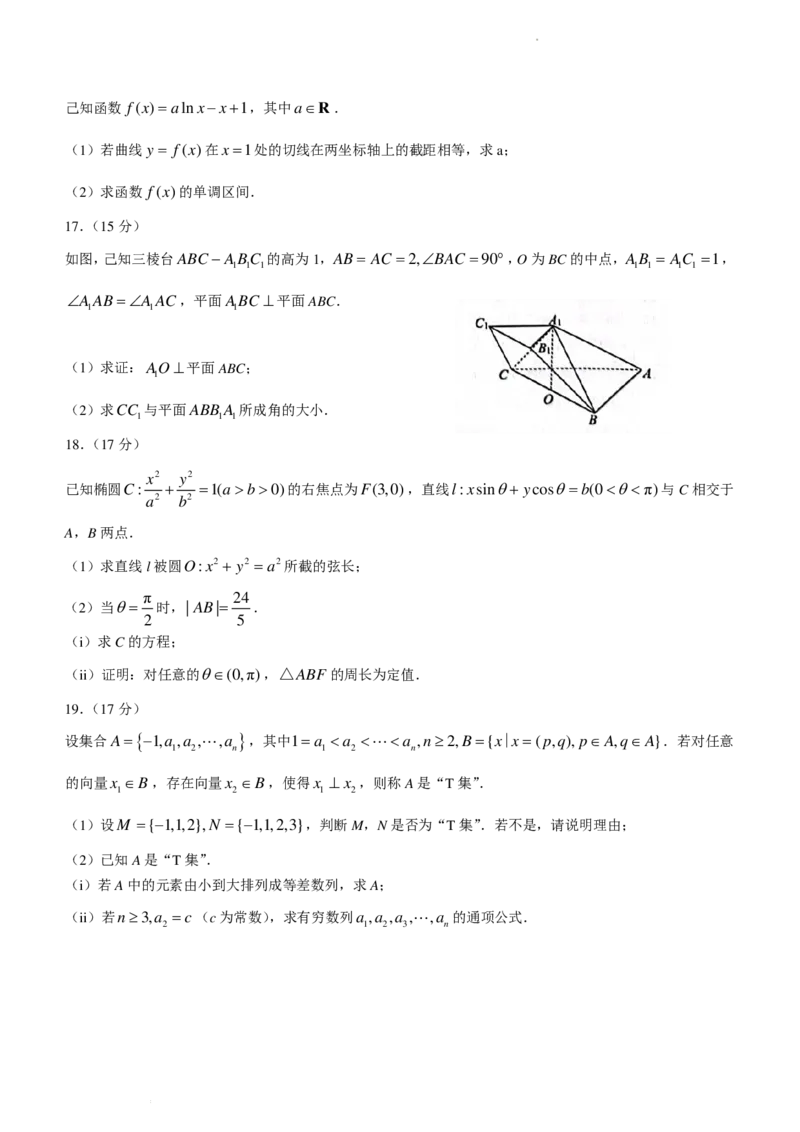
如图,己知三棱台ABC−ABC 的高为1,AB= AC =2,∠BAC =90°,O为BC的中点,AB = AC =1,
1 1 1 1 1 1 1
∠AAB=∠AAC,平面ABC ⊥平面ABC.
1 1 1
(1)求证:AO⊥平面ABC;
1
(2)求CC 与平面ABB A 所成角的大小.
1 1 1
18.(17分)
x2 y2
已知椭圆C: + =1(a >b>0)的右焦点为F(3,0),直线l:xsinθ+ ycosθ=b(0<θ<π)与C相交于
a2 b2
A,B两点.
(1)求直线l被圆O:x2 + y2 =a2所截的弦长;
π 24
(2)当θ= 时,| AB|= .
2 5
(i)求C的方程;
(ii)证明:对任意的θ∈(0,π),△ABF 的周长为定值.
19.(17分)
设集合A={−1,a ,a ,,a },其中1=a