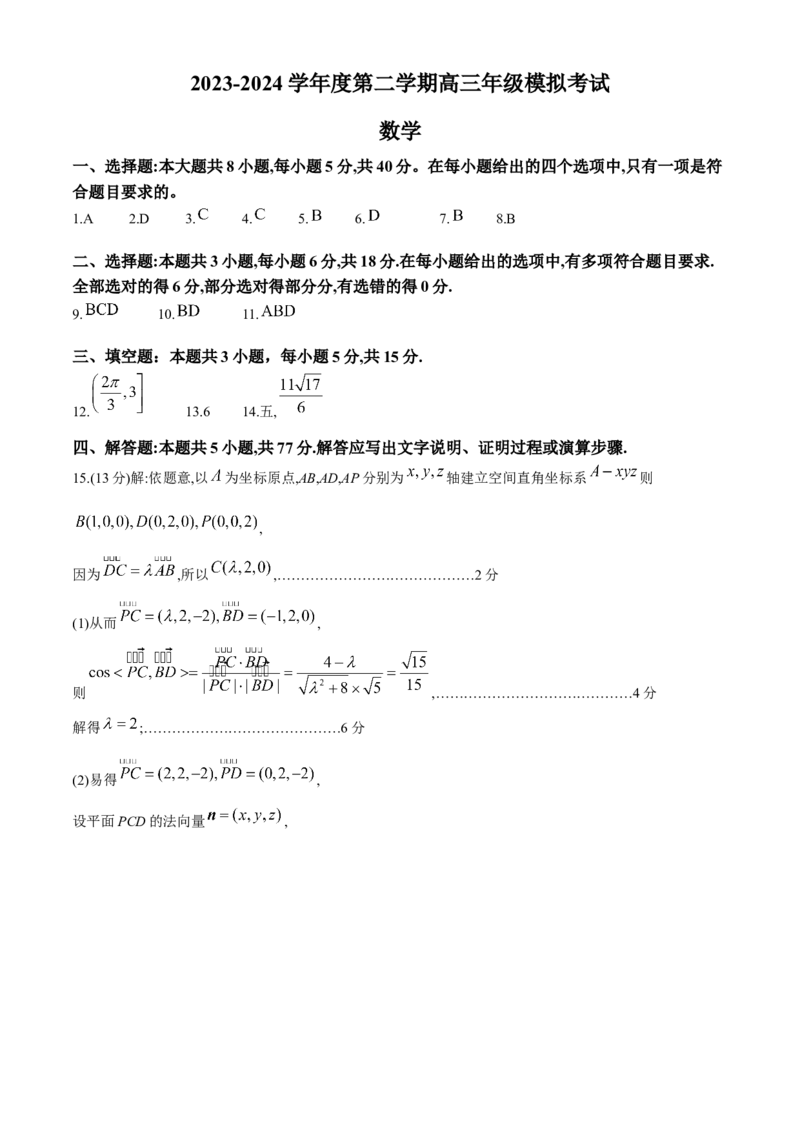文档内容
江苏省南通市海安高级中学 2023-2024 学年高三下学期第二次模拟考
试数学试题
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符
合题目要求的。
1.已知复数 (其中 为虚数单位, ).若 是纯虚数,则 ( )
A.-4 B.-1 C.1 D.4
2.直线 的倾斜角为( )
A. B. C. D.
3.有6名男教师和5名女教师,从中选出2名男教师、1名女教师组成一个支教小组,则不同的选法共有( )
A.60种 B.70种 C.75种 D.150种
4.已知等差数列 的前 项和为 ,且 ,则 是 中的( )
A.第28项 B.第29项 C.第30项 D.第32项
5.在 中,已知 ,则“ ”是“ ”成立的( )条件
A.充分不必要 B.必要不充分 C.充分必要 D.既不充分也不必要
6.已知双曲线 ,直线 .双曲线 上的点 到直线 的距离最小,则点 的横坐
标为( )
A. B. C. D.
7.若命题:“ ,使得 ”为假命题,则a,b的大小关系为( )
A. B. C. D.
8.设实数 满足 ,则 的最小值为( )
A. B. C. D.-1
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.
全部选对的得6分,部分选对得部分分,有选错的得0分.
9.下列可以反映总体数据集中趋势的统计特征数为( )A.方差 B.平均数 C.中位数 D.众数
10.已知不等式 对任意 恒成立,其中 是整数,则 的取值可以为( )
A.-4 B.-2 C.0 D.8
11.直线 与抛物线 相交于 两点,过 两点分别作该抛物线的切线,与直线
均交于点 ,则下列选项正确的是( )
A.直线 过定点 B. 两点的纵坐标之和的最小值为2p
C.存在某一条直线 ,使得 为直角
D.设点 在直线 上的射影为 ,则直线FH斜率的取值范围是
三、填空题:本题共3小题,每小题5分,共15分.
12.已知集合 ,则 ___________.
13.设 若 ,则 ___________.
14.在长方体 中, 分别是棱 的中点,则平面CEF截
该长方体所得的截面为___________边形,截面面积为___________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)如图,在四棱锥 中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2,若 ,且向量
与 夹角的余弦值为 .
(1)求实数 的值;
(2)求直线PB与平面PCD所成角的正弦值.16.(15分)已知向量 .设 .
(1)求函数 的单调递增区间;
(2)在 中,若 的平分线交BC于点 ,求AD长.
17.(15分)在平面直角坐标系xOy中,设椭圆 的离心率为 分别是椭圆的
左、右焦点,过 作两条互相垂直的直线 ,直线 与 交于A,B两点,直线 与 交于D,E两点,且
的周长是 .
(1)求椭圆 的方程;
(2)当 时,求 的面积.
18.(17分)设函数 .
(1)若 ,求函数 的单调区间;
(2)若 ,试判断函数 在区间 内的极值点的个数,并说明理由;
(3)求证:对任意的正数 ,都存在实数 ,满足:对任意的 .
19.(17分)“踩高跷,猜灯谜”是我国元宵节传统的文化活动.某地为了弘扬文化传统,发展“地推经济”,在元
宵节举办形式多样的猜灯谜活动.
(1)某商户借“灯谜”活动促销,将灯谜按难易度分为B、C两类,抽到较易的 类并答对购物打八折优惠,抽
到稍难的 类并答对购物打七折优惠.抽取灯谜规则如下:在一不透明的纸箱中有8张完全相同的卡片,其中
3张写有 字母,3张写有 字母,2张写有 字母,顾客每次不放回从箱中随机取出1张卡片,若抽到写有
的卡片,则再抽1次,直至取到写有 或 卡片为止.求该顾客取到写有 卡片的概率.
(2)小明尝试去找全街最适合他的灯谜,规定只能取一次,并且只可以向前走,不能回头,他在街道上一共会遇到
条灯谜(不妨设每条灯谜的适合度各不相同),最适合的灯谜出现在各个位置上的概率相等,小明准备采
用如下策略:不摘前 条灯谜,自第 条开始,只要发现比他前面见过的灯谜适合的,就摘这条灯谜,否则就摘最后一条.设 ,记小明摘到那条最适合的灯谜的概率为 .
①若 ,求 ;
②当 趋向于无穷大时,从理论的角度,求 的最大值及 取最大值时 的值.
(取 )2023-2024 学年度第二学期高三年级模拟考试
数学
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符
合题目要求的。
1.A 2.D 3. 4. 5. 6. 7. 8.B
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.
全部选对的得6分,部分选对得部分分,有选错的得0分.
9. 10. 11.
三、填空题:本题共3小题,每小题5分,共15分.
12. 13.6 14.五,
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)解:依题意,以 为坐标原点,AB,AD,AP分别为 轴建立空间直角坐标系 则
,
因为 ,所以 ,……………………………………2分
(1)从而 ,
则 ,……………………………………4分
解得 ;……………………………………6分
(2)易得 ,
设平面PCD的法向量 ,则 ,且 ,
即 ,且 ,所以 ,
不妨取 ,则平面PCD的一个法向量 ,…………………………………………9分
又易得 ,
故 ,………………………………………………12分
所以直线PB与平面PCD所成角的正弦值为 .………………………………………………13分
16.(15分)解:(1)由
……………………………………………………………………………………4分
令 ,则 ,
所以函数的单调递增区间为 .…………………………………………7分
(2)因 ,因为 ,所以 ,即 ,故 ;…………………………………………………………9分
由余弦定理得 ,即 ,
所以 (负舍),……………………………………………………………………………11分
所以 ,
即 ,
所以 .………………………………………………………………………………………15分
17.(15分)解:(1)由 ,知 ,所以 ,……………………………2分
因为 的周长是 ,所以 ,……………………………4分
所以 ,故 ,
所以椭圆 的方程为 .…………………………………………………………6分
(2)分析知直线 的斜率存在,且不为0,设 的方程为: ,
与椭圆方程联立:
,得 ,……………………………8分
同理: ,……………………………………………………10分
所以 ,解得 ,…………………………………………12分所以 ,直线 的方程为 ,
所以 ,故 .……………………………………………15分
18.(17分)解:(1)当 时, ,
令 ,列表分析
1
— 0 +
单调递减 单调递增
故 的单调递减区间为 ,单调递增区间为 .………………………………4分
(2) ,其中 ,
令 ,分析 的零点情况.
,令 ,列表分析
— 0 +
单调递减 单调递增
...........6分
因为 ,
所以 ,即 ,
而 ,
因此 在 有一个零点, 在 内有一个极值点;当 时, 在 内有一个极值点.……………………………………10分
(3)猜想: 恒成立.……………………………………………11分
证:由(2)得 在 上单调递增,
且 .
因为当 时, ,所以 .
故 在 上存在唯一的零点,设为 .
由
- 0 +
单调递减 单调递增
知, .…………………………………………13分
又 ,而 时, ,
所以 .
即 .
所以对任意的正数 ,存在 ,使对任意的 ,使 .……………………15分
补充证明(*):
令 ,所以 在 上单调递增.
所以 时, ,即 .
补充证明(**)
令 ,所以 在 上单调递减.
所以 时, ,即 .……………………………………………………17分19.(17分)解:(1)该顾客第一次取到写有 卡片的概率为 ,……………………………………..1分
该顾客第二次取到写有 卡片的概率 ,………………………………………………..2分
该顾客第三次取到写有 卡片的概率 ,……………………………………………3分
该顾客第四次取到写有 卡片的概率 ,………………………………………4分
该顾客取到写有 卡片的概率为 ;……………………………………5分
(2)①这4条灯谜的位置从第1个到第4个排序,有 种情况,………………………………7分
要摘到那条最适合灯谜,有以下两种情况:
(i)最适合灯谜是第3个,其它的随意在哪个位置,有 种情况;
(ii)最适合灯谜是最后1个,第二适合灯谜是第1个或第2个,其它的随意在哪个位置,有 种情况,
………………………………………………………………………………………………………………9分
故所求概率为 ;……………………………………………………………………………………10分
②记事件 表示最适合灯谜被摘到,事件 表示最适合灯谜排在第 个,
则 ,
由全概率公式知: ,
当 时,最适合灯谜在前 条中,不会被摘到,此时 ;
当 时,最适合灯谜被摘到,当且仅当前 条灯谜中的最适合那条在前 个之中时,
此时 ,所以 ,………………………………………………………14分
令 ,则 ,
由 ,得 ,
当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 ,所以当 时, 取得最大值 ,
从而 的最大值为 ,此时 的值为 .…………………………………………………………………17分