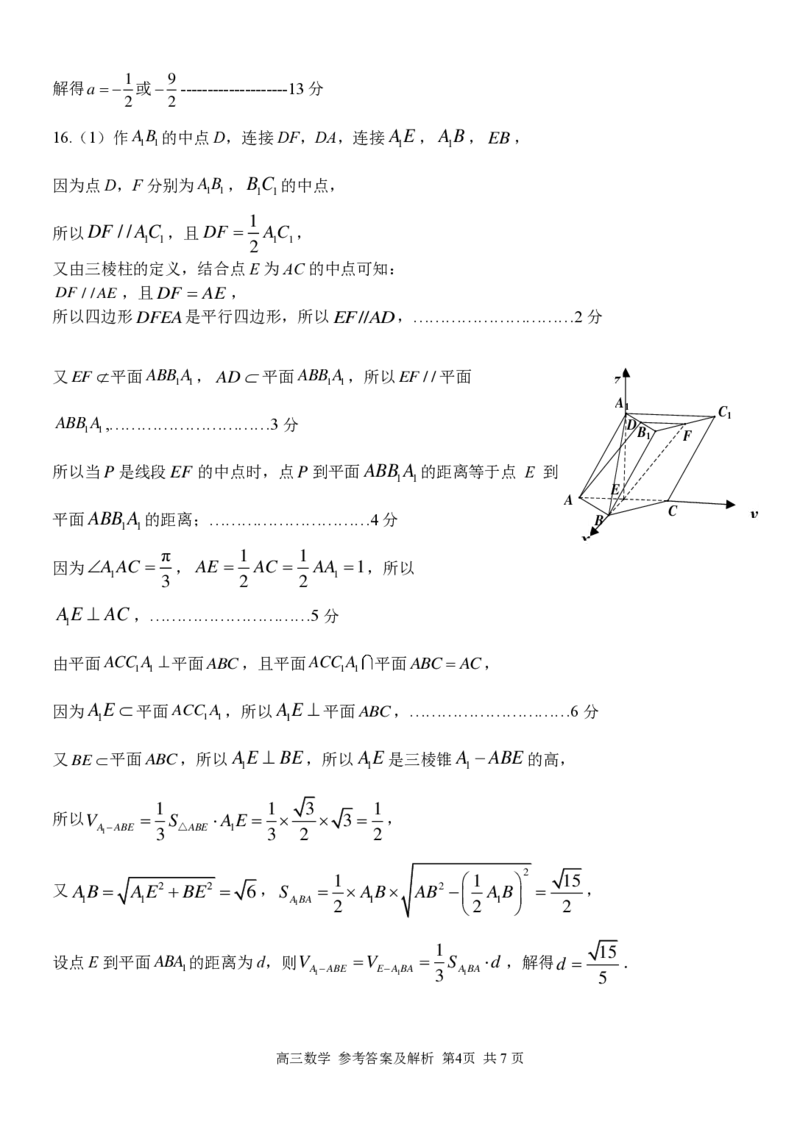浙江卷浙江省2023学年第二学期浙江精诚联盟适应性联考)(5.15-5.17)数学试卷答案_2024年5月_01按日期_21号_2024届浙江省第二学期浙江精诚联盟适应性联考

2023 学年第二学期浙江精诚联盟适应性联考
高三数学学科 参考答案及解析
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合
题目要求的.
1．A 解析：
高三数学 参考答案及解析 第1页 共7页
B = R  A B = R ，故选A．
2．B 解析： T
r + 1
= C r3 ( x 2 ) 3 − r  − 1
2 x

r
为常数项，则 r = 2 ，所以 T
3
= C 23 1
4
= 3
4
， 故选B．
3．D 解析：设 z = a + b i ， a , b  R ，则 a = − 2 ， b = 1 ．  z = − 2 + i , z = − 2 − i ，所以 z  z = 5 ，
故选D．
4．C 解析：若残留量不足初始量的50%，则 y
0
 e
t2
ln 0 .8
 0 .5 y
0
， ( 0 . 8 )
t2
 0 . 5 ，两边取常用对数
t
2
l g 0 . 8  l g 0 . 5 ， t 
−
3 l
2
g
l
2
g
−
2
1
 6 .2 ，所以至少需要7年．故选C．
5．C 解析：当 n  2 0 2 3 时， S
n
= S
4 0 4 7 − n
 0 = a
n + 1
+ a
n + 2
+ ... + a
4 0 4 7 − n
=
a
n + 1
+
2
a
4 0 4 7 -n ( 4 0 4 7 − 2 n )
，得 a
2 0 2 4
= 0 ；当 n  2 0 2 3 时， S
n
= S
4 0 4 7 − n
 0 = a
4 0 4 8 − n
+ a
4 0 4 6 − n
+ ... + a
n
=
a
n
+ a
2
4 0 4 8 -n ( 4 0 4 7 − 2 n )
，得 a
2 0 2 4
= 0 ，易得“ a
2 0 2 4
= 0 ”是“ S
n
= S
4 0 4 7 − n
( n  4 0 4 7 , n  N  ) ”的充要条件，故选C．
6．A 解析： c o s
2
π
3
c o s
2
π
6
1
2
c o s
π
6
c o s
π
2
1
4
 


+
 
−

=
 
+

+

= ，
c o s
π
6
1
2
 

+

=
 π  π 1
，cos  2+  =2cos2  +  −1=− ，故选A．
 3  6 2
1 1 1
7．A 解析：集合A中的函数为奇函数的有y = x+ ，y = x− ，y = −x，而有单调递减区
x x x
间的函数有 y = x +
1
x
和 y =
1
x
− x ，所以概率为
2
3
，故选A．
8．A 解析：设 F A =t，由
2
S
△ C O F 2
= 2 S
△ A F F1 2
易得 FC =4t = FC ， 又
2 1
a
FC ⊥FA, AC =5t，FA =3t，又 AF + AF =2a=4t，t = ，在△CFO中，
1 1 1 1 2 2 2
2 2 2
c AF + FF − AF
cosCFO= ．在△AF F中，cosAF F = 2 1 2 1 ，
2 2a 2 1 2 1 2 F A FF
2 1 2
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}高三数学 参考答案及解析 第2页 共7页
c o s  A F
2
F
1
+ c o s  C F
2
O = 0
10
．解得e= ，故选A．
5
二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要
求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9．AD 解析：对于A选项，原数据的平均数为8，插入一个数8，平均数不变，正确；
对于B选项，取 a = − 2 , b = 1 ，原数据的中位数为9，新数据的中位数为8.5，错误；
对于C选项，新数据的方差为 s  2 =
1
1
0
 ( 2 + a − 8 ) 2 + ( 3 − 8 ) 2 + ( 1 3 − 8 ) 2 + ( 8 − 8 ) 2 

1
9
 ( 2 + a − 8 ) 2 + ( 3 − 8 ) 2 + ( 1 3 − 8 ) 2  = s 2 ，错误；
对于D选项，因为 3  8  1 3 ，所以8不是最值，故新数据的极差不变，正确．故选AD
………………………按0，3，6分给分
10．ABD 解析：对于A选项，由平面与平面垂直的性质定理可知，A正确；
对于B选项，在内作a的垂线，则此垂线必垂直于，自然也就垂直内的已知直线.这种垂线可
以作无数条，所以B正确；

对于C选项，b与所成的角为 ，但
6
b 与的位置关系不确定，特殊情况下可以是 b //，所以
C错误；对于D选项，由最小角定理可知，D正确．故选ABD．
………………………按0，2，4，6分给分
11．ABD 解析：取 n = 2 ，ABD正确，C显然错误．
对于不等式 ln x x − 1 ，当且仅当 x = 1 时，等号成立，
1
对于A选项，令x=1+ (n 2)，所以
n
ln

1 +
1
n

 1 +
1
n
− 1 =
1
n
，
故 ln

1 +
1
1

+ ln

1 +
1
2

+ + ln

1 +
n
1
− 1

 1 +
1
2
+ +
n
1
− 1
，
其中 ln

1 +
1
1

+ ln

1 +
1
2

+ + ln

1 +
n
1
− 1

= ln 2 − ln 1 + ln 3 − ln 2 + + ln ( n ) − ln ( n − 1 )
1 1 1
=ln(n)−ln1=ln(n)，所以ln(n)1+ + + + ，A正确；
2 3 n−1
对于B选项，将x替换为 1 − x ，可得ln(1−x) 1−x−1=−x，当且仅当x=0时等号成立.令 x =
1
n
 0 ，
 1 1 1
可得ln1− − ，所以lnn−ln(n−1) ，
 n n n
1 1 1
故ln2−ln1+ln3−ln2+ +ln2n−ln(2n−1) + + + ，
2 3 2n
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}得
高三数学 参考答案及解析 第3页 共7页
ln ( 2 n ) 
1
2
+
1
3
+ +
1
2 n
，所以 ln ( n ) 
1
2
+
1
3
− ln 2 +
1
4
+ +
1
2 n

1
4
+ +
1
2 n
，所以B正确;
1 n 2 n n n e
对于D选项，等价于证明   +  + +   ，将
n n n e−1
ln x x − 1 中的x替换为
i
n
，其中 i  N * ，
n  N *
i i
，则 ln −1，则
n n
n ln
i
n
i − n ，故
 i
n
 n
e i− n ，当且仅当 i = n 时，等号成立，则
 1
n
 n
+
 2
n
 n
+ +
 n
n
 n
 e 1− n + e 2 − n + + e n − n =
e 1− ( n
1
1
−
−
e
e n )
=
e −
e
e
−
1−
1
n

e
e
− 1
，D正确．故选ABD．
………………………按0，2，4，6分给分
三、填空题：本题共3小题，每小题5分，共15分.
12． 1
6
2 解析：由P(60 X 100)= ，
3
X 服从正态分布 N ( 8 0 , 2 )  ，故
P ( X  6 0 ) =
1
2
(1 −
2
3
) =
1
6
.
13．4051 解析：因为函数 y = f ( x + 2 ) − 1 为定义在 R 上的奇函数，所以函数 f ( x ) 关于 ( 2 , 1 ) 中
心对称，
4051
i=1 f ( i − 2 0 2 4 ) = [ f ( − 2 0 2 3 ) + f ( 2 0 2 7 ) ] + [ f ( − 2 0 2 2 ) + f ( 2 0 2 6 ) ] + … + [ f (1 ) + f ( 3 ) ] + f ( 2 )
= 2 0 2 5  2 + 1 = 4 0 5 1 ．
14．25 解析：设△ABC的外接圆圆心为O，取弦 E F 的中点 H ，则 P E  P F = P H
2
− 1 6 ，
因为 P E  P F 的最大值为 48，所以 P H
m a x
= 8 .由圆的相关知识可知，当 P 、 H 、 O 三点共线时
P H 最大.在 △ O H E 中， r 2 = ( 8 − r ) 2 + 1 6 ，所以圆的半径为 5，所以△ABC的面积的最大值为
25．
四、解答题：本题共5小题，共77分.解答时应写出文字说明、证明过程或演算步骤.
15．（1）易知 f(x)定义域为R， f ( x ) =
2 −
e x
x
，---------------------2分
所以 x  ( −  , 2 ) , f ( x )  0 , x  ( 2 , +  ) , f ( x )  0 . ---------------------4分
故 f(x)单调增区间：(−,2)，单调减区间：(2,+).-----------------6分
（2）因为 f(0)=2，f(0)=0，--------------------8分
所以曲线 y = f ( x ) 在点(0,0)处的切线为y=2x--------------------9分
把切线方程y=2x代入二次曲线方程y=ax2 +（2a+5）x−2，得ax2 +（2a+3）x−2=0有唯一解，
即=0且a0，即4a2 +20a−9=0---------------------12分
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}1 9
解得a=− 或− --------------------13分
2 2
16.（1）作
高三数学 参考答案及解析 第4页 共7页
A
1
B
1
的中点D，连接DF，DA，连接 A
1
E ， A
1
B ， E B ，
因为点D，F分别为 A
1
B
1
，BC 的中点，
1 1
所以 D F / / A
1
C
1
，且 D F =
1
2
A
1
C
1
，
又由三棱柱的定义，结合点E为AC的中点可知：
D F / / A E ，且 D F = A E ，
所以四边形 D F E A 是平行四边形，所以 E F / / A D ，…………………………2分
又 E F  平面 A B B
1
A
1
， A D 平面 A B B
1
A
1
，所以 E F / / 平面
A B B
1
A
1
,…………………………3分
所以当 P 是线段EF 的中点时，点 P 到平面ABB A 的距离等于点 E 到
1 1
平面 A B B
1
A
1
的距离；…………………………4分
因为  A
1
A C =
π
3
， A E =
1
2
A C =
1
2
A A
1
= 1 ，所以
A
1
E ⊥ A C ，…………………………5分
由平面 A C C
1
A
1
⊥ 平面 A B C ，且平面 A C C
1
A
1
平面 A B C = A C ，
因为 A
1
E  平面 A C C
1
A
1
，所以 A
1
E ⊥ 平面ABC，…………………………6分
又 B E  平面 A B C ，所以 A
1
E ⊥ B E ，所以AE是三棱锥A −ABE的高，
1 1
1 1 3 1
所以V = S AE =   3 = ，
A 1 −ABE 3 △ABE 1 3 2 2
又 A
1
B = A
1
E 2 + B E 2 = 6
z
A
1 C
1 D
B 1 F
E
A
C y
B
x
2
1 1  15
，S = AB AB2 − AB = ，
 
A 1 BA 2 1 2 1  2
1 15
设点E到平面ABA的距离为d，则V =V = S d ，解得d = ．
1 A 1 −ABE E−A 1 BA 3 A 1 BA 5
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}即点P到平面
高三数学 参考答案及解析 第5页 共7页
A B B
1
A
1
的距离为
1
5
5
.…………………………8分
（2）以 E B 为 x 轴， E C 为 y 轴， E A
1
为 z 轴建立空间直角坐标系，
E ( 0 , 0 , 0 ) ， B ( 3 , 0 , 0 ) ， B
1
( 3 , 1 , 3 ) ， C
1
( 0 , 2 , 3 ) ，C(0,1,0)，
3 3
所以F( , , 3)，BC =(− 3,1,0)，
2 2
C C
1
= ( 0 , 1 , 3 ) ， E F = (
2
3
,
3
2
, 3 ) ，
设 E P E F ( 0 1 )   = ，则 P C (
2
3
, 1
3
2
, 3 )    = − − − ，…………………………10分
设平面 P C C
1
的一个法向量 n
1
= ( x
1
, y
1
, z
1
) ，
则有
 n
n
1
1
 P
 C
C
C
1
=
=
0
0
，所以 n
1
(
2
1 , 3 , 1 )

= − − ，…………………………11分
设平面 B B
1
C
1
C 的一个法向量 n
2
= ( x
2
, y
2
, z
2
) ，
则有
 n
n
2
2
 B
 C
C
C
1
=
=
0
0
，所以n =(1, 3,−1)，…………………………12分
2
所以 c o s n
1
, n
2
n
n
1
1
n
2
n
2 (
2
2
1 )
1
2
3
3
1
1 5
9
1
1
4
4
5
5 

  =


=
−
− +
+
+
+ 
= ，
1
解得= 或
3
1 3
3
 = （舍去）. …………………………14分
所以 E P =
1
3
E F =
1
3
3
4
+
9
4
+ 3 =
3
6 6
.即EP的长为 .…………………………15分
3
1+d =q
17．解析：（1）设公比为q,公差为d,则 ……………3分
3q2 =4(1+2d)
 2
q=
q=2   3
解得 或 (舍去)……………5分
d =1
d =−
1
 3
所以a =2n−1,b =n……………7分
n n
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}（2）
高三数学 参考答案及解析 第6页 共7页
T = 1
n
 2
2 T
0
n
+
=
2
1 

2
2
1
1
+
+
2
3 2  2
2  2
+
+
.... +
.... +
n
( n
 2
−
n −
1 )
1
 2 n + n  2 n
……………8分
所以 T
n
= − ( 2 0 + 2 1 + 2 2 + .... + 2 n − 1 ) + n  2 n = ( n − 1 )  2 n + 1 ……………10分
故
b
n
T

nb
n + 1
=
( n −
n (
1
n
) 2
+
n
1
+
)
1
=
( n
n (
−
n
1
+
) 2
1
n
)
+
n ( n
1
+ 1 )
(n−1)2n 2n+1 2n 1 1 1
得 = - ， = − …13分（一个裂项正确得2分，两个正确得3分）
n(n+1) n+1 n n(n+1) n n+1
所以 P
n
=
2
n
n +
+
1
1
− 1 −
n
1
+ 1

2
n
n +
+
1
1
− 1 ．…………15分
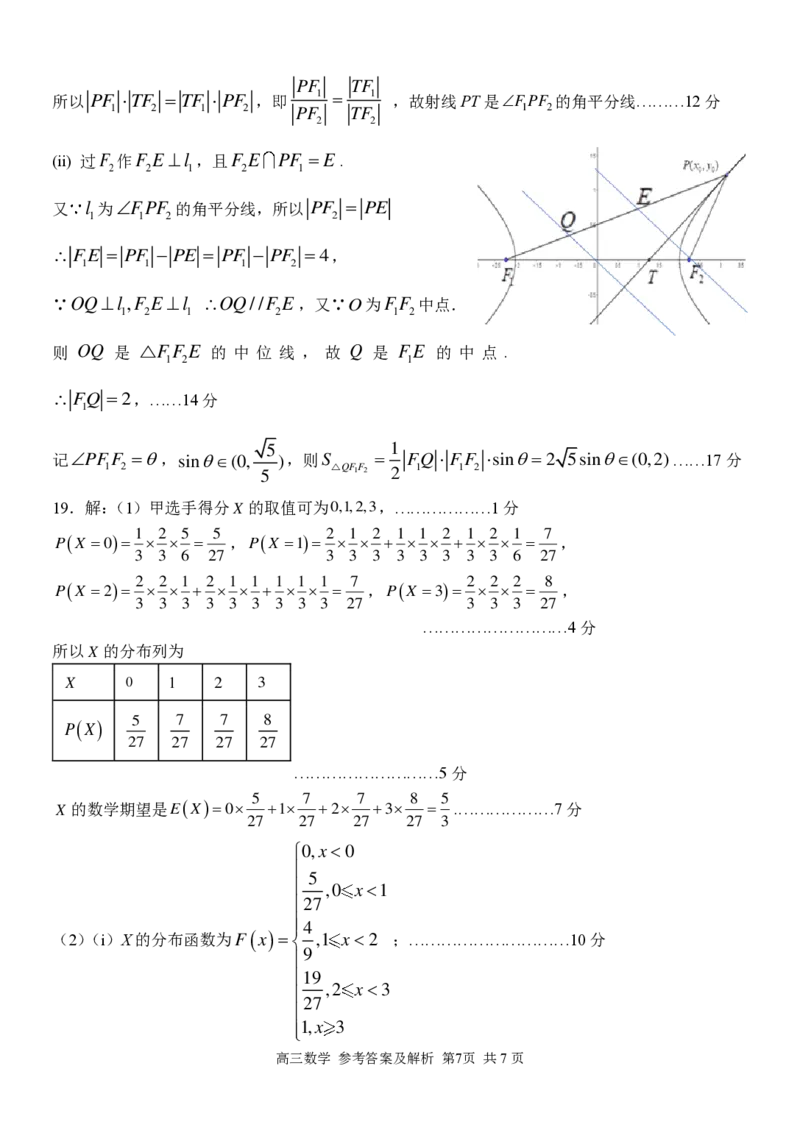
18．解析：（1） 实轴长为 4  2 a = 4 即 a = 2 ，又 右 焦 点 到 渐 近 线 距 离 为 1 ，∴
b = 1 ，…………3分
故双曲线  的标准方程为  :
x
4
2
− y 2 = 1 ．…………5分
(2) (i) 设 P ( x
0
, y
0
) ， 切 线 l ： y−y =k(x−x ) ， 则
1 0 0
x 20 − 4 y 20 = 4 ，联立
x2
 − y2 =1
 4 化 简 得 ：
 y− y =k(x−x )
 0 0
 1
4
− k 2

x 2 − 2 k ( y
0
− k x
0
) x − ( y
0
− k x
0
) 2 − 1 = 0 …………7分
由  = 0 , 解得： k =
4
x
0
y
0
，所以直线PT： y − y
0
=
4
x
0
y
0
( x − x
0
) ，令 y = 0 ，得： T (
4
x
0
, 0 ) ，…………8分
4 4
故 TF = + 5，TF =− + 5…………9分
1 x 2 x
0 0
5 5
因 为 PF = (x + 5)2+ y2 = x 2+ 5x +4 =2+ x ， 所 以
1 0 0 4 0 0 2 0
5
PF = PF −4= x −2，…………10分
2 1 2 0
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}PF TF
所以 PF TF = TF  PF ，即 1 = 1 ，故射线PT是
1 2 1 2 PF TF
2 2
高三数学 参考答案及解析 第7页 共7页
 F
1
P F
2
的角平分线………12分
(ii) 过 F
2
作 F
2
E ⊥ l1 ，且 F
2
E P F
1
= E .
又 l1 为  F
1
P F
2
的角平分线，所以 P F
2
= P E
FE = PF − PE = PF − PF =4，
1 1 1 2
∵OQ⊥l ,F E ⊥l
1 2 1
 O Q / / F
2
E ，又∵ O 为 F
1
F
2
中点．
则 O Q 是 △ F
1
F
2
E 的 中 位 线 ， 故 Q 是 F
1
E 的 中 点 .
 F
1
Q = 2 ，……14分
记 P F
1
F
2
  = ， s i n ( 0 ,
5
5
)  
1
，则S = FQ  FF sin=2 5sin(0,2)……17分
△QF 1 F 2 2 1 1 2
19．解：（1）甲选手得分 X 的取值可为0,1,2,3，………………1分
P ( X = 0 ) =
1
3

2
3

5
6
=
5
2 7
， P ( X = 1 ) =
2
3

1
3

2
3
+
1
3

1
3

2
3
+
1
3

2
3

1
6
=
7
2 7
，
P ( X = 2 ) =
2
3

2
3

1
3
+
2
3

1
3

1
3
+
1
3

1
3

1
3
=
7
2 7
， P ( X = 3 ) =
2
3

2
3

2
3
=
8
2 7
，
………………………4分
所以 X 的分布列为
X 0 1 2 3
P ( X )
5
2 7
7 7 8
27 27 27
………………………5分
X
5 7 7 8 5
的数学期望是E(X)=0 +1 +2 +3 = .………………7分
27 27 27 27 3
0,x0

5
 ,0 x1
27

4
（2）（i）X的分布函数为F(x)= ,1 x2 ；…………………………10分
9

19
,2 x3

27

 1,x 3
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}（ii）设随机变量Y的分布函数为
高三数学 参考答案及解析 第8页 共7页
G ( x ) ，
若x0，此时G(x)=0；………………………11分
若 0 x 2 ，由题意设 P ( 0 Y x ) = k x 2 ，
当 x = 2 时，有 P ( 0 Y 2 ) = k  2 2 = 4 k ，又因为 P ( 0 Y 2 ) = 1 ，
1 x2
所以k = ，即P(0 Y x)= ，
4 4
所以 G ( x ) = P ( Y x ) = P ( Y  0 ) + P ( 0 Y x ) =
x
4
2
；………………………15分
若 x 2 ，此时G(x)=P(Y x)=1，………………………16分
综上所述， G ( x ) =
 0 , x
2 x
4
1 , x
,

0
2
0
x  2 .…………………………17分
{#{QQABCYiAogCgAJAAABgCQwEyCkCQkBACAIoOxEAIMAAAyQFABAA=}#}