文档内容
集宁二中 2024-2025 学年下学期高二年级月考检测卷
数学
注意:本试卷包含两卷,第一卷为选择题,所有答案必须用 2B 铅笔涂在答题卡中相应的位置
.第二卷为非选择题,所有答案必须填在答题卡的相应位置,答案写在试卷上均无效,不予记
分.
第一卷
一、单选题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的选项中,只有一项是符合
题目要求的.
1. 在等差数列 中, , ,则 ( )
A. 17 B. 18 C. 19 D. 20
2. 已知函数 ,则 ( )
A. 2 B. C. 4 D.
3. 已知函数 ( 是 的导函数),则 ( )
A. B. C. D.
4. 已知函数 存在单调递减区间,则 的取值范围是
A. B. C. D.
5. 已知 在 处的极大值为 5,则 ( )
A B. 6
C. 或 6 D. 或 2
6. 已知函数 ,则关于 不等式 的解集为( )
A. B.
C. D.
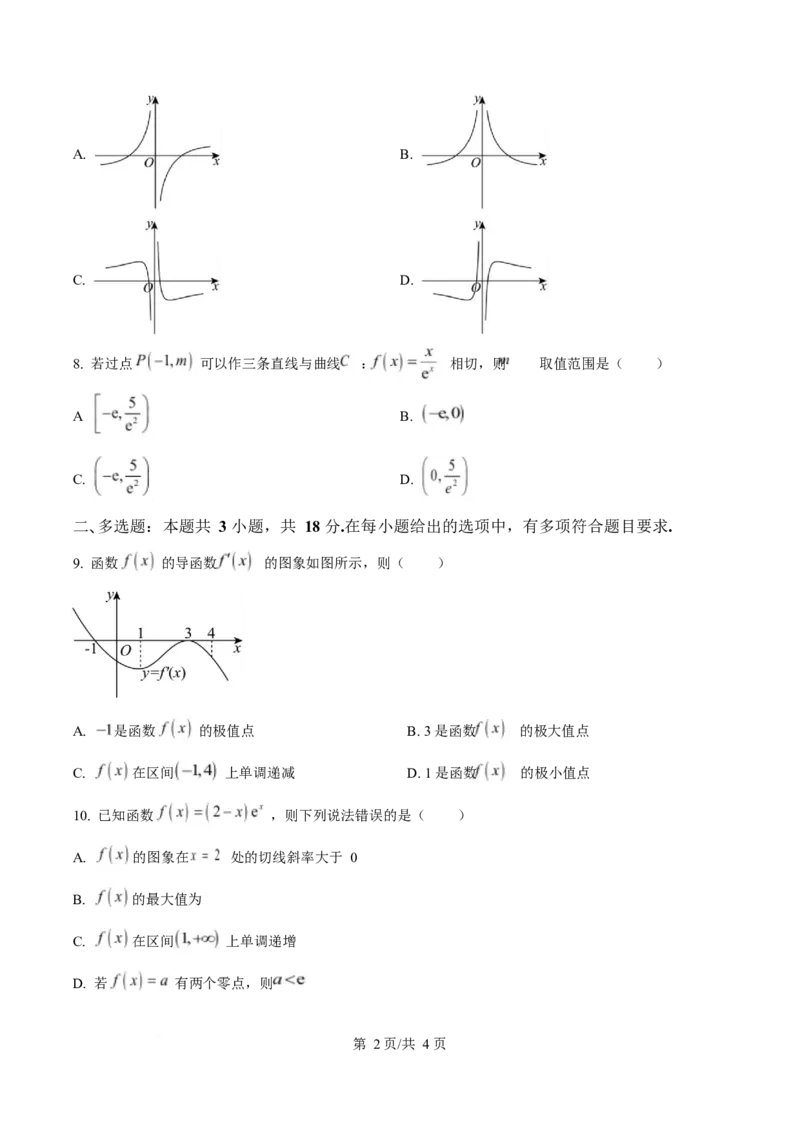
7. 函数 的图象大致是( )
第 1页/共 4页A. B.
C. D.
8. 若过点 可以作三条直线与曲线 : 相切,则 取值范围是( )
A B.
C. D.
二、多选题:本题共 3 小题,共 18 分.在每小题给出的选项中,有多项符合题目要求.
9. 函数 的导函数 的图象如图所示,则( )
A. 是函数 的极值点 B. 3 是函数 的极大值点
C. 在区间 上单调递减 D. 1 是函数 的极小值点
10. 已知函数 ,则下列说法错误的是( )
A. 的图象在 处的切线斜率大于 0
B. 的最大值为
C. 在区间 上单调递增
D. 若 有两个零点,则
第 2页/共 4页11. 关于函数 , ,下列说法不正确的是( )
A. 当 时, 在 上单调递增 B. 当 时, 恒成立
C. 当 时, 在 上单调递增 D. 当 恒成立,则
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12. 函数 的极小值点为______.
13. 已知函数 在区间 上不单调,则 m 的取值范围是______
.
14. 若直线 与曲线 相切,则 的最大值为______.
四、解答题:本题共 6 小题,共 77 分.解答应写出文字说明,证明过程或演算步骤.
15. 已知函数 ,a 为实数.
(1)当 时,讨论 的单调性;
(2)若 在区间 上是减函数,求 a 的取值范围.
16. 已知函数 , .
(1)讨论函数 的单调性;
(2)求函数 在区间 上的最小值.
17. 已知函数 .
(1)求曲线 在点 处的切线方程;
(2)求 的极值;
(3)若对于任意 ,不等式 恒成立,求实数 的取值范围.
18. 已知函数 .
(1)当 时,求函数 在 上 值域;
(2)若函数 在 上仅有两个零点,求实数 的取值范围.
19. 已知函数 , .
第 3页/共 4页(1)若函数 存在两个极值,求 的取值范围;并证明:函数 存在唯一零点.
(2)若存在实数 , ,使 ,且 ,求 的取值范围.
第 4页/共 4页