文档内容
武昌区 2024 届高三年级 5 月质量检测
数学
本试题共19题,满分150分,考试用时120分钟
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 若复数 满足 ,则 的虚部为( )
A. B. C. D.
2. 已知二项式 展开式的二项式系数的和为64,则 ( )
A. B.
C. 展开式的常数项为 D. 的展开式中各项系数的和为1
3. 已知 ,向量 ,且 ,则 在 上的投影向量为( )
.
A B. 5 C. D.
4. 已知等差数列 的前 项和为 ,若 ,则 ( )
A. 288 B. 144 C. 96 D. 25
5. 已知函数 ,则关于 的不等式 的解集为( )
A. B. C. D.
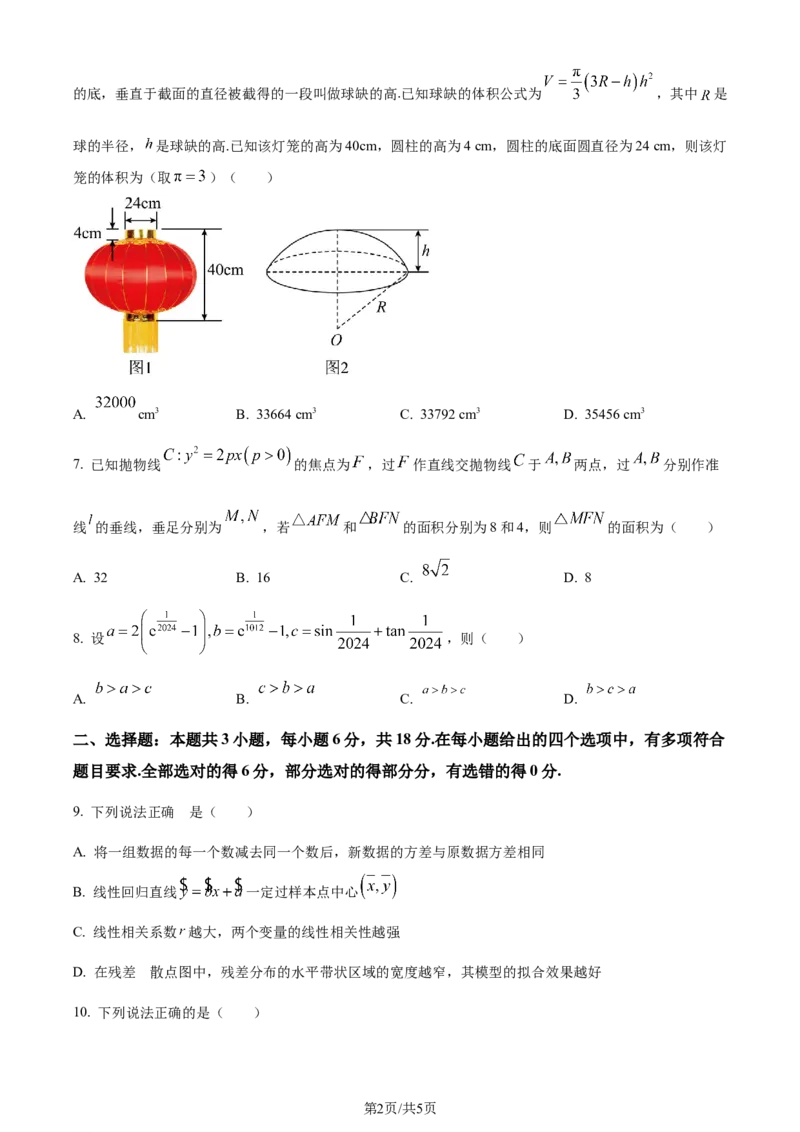
6. 灯笼起源于中国的西汉时期,两千多年来,每逢春节人们便会挂起象征美好团圆意义的红灯笼,营造一
种喜庆的氛围.如图1,某球形灯笼的轮廓由三部分组成,上下两部分是两个相同的圆柱的侧面,中间是球
面的一部分(除去两个球缺).如图2,“球缺”是指一个球被平面所截后剩下的部分,截得的圆面叫做球缺
第1页/共5页
学科网(北京)股份有限公司的底,垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为 ,其中 是
球的半径, 是球缺的高.已知该灯笼的高为40cm,圆柱的高为4 cm,圆柱的底面圆直径为24 cm,则该灯
笼的体积为(取 )( )
A. cm3 B. 33664 cm3 C. 33792 cm3 D. 35456 cm3
7. 已知抛物线 的焦点为 ,过 作直线交抛物线 于 两点,过 分别作准
线 的垂线,垂足分别为 ,若 和 的面积分别为8和4,则 的面积为( )
A. 32 B. 16 C. D. 8
8. 设 ,则( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
的
9. 下列说法正确 是( )
A. 将一组数据的每一个数减去同一个数后,新数据的方差与原数据方差相同
B. 线性回归直线 一定过样本点中心
C. 线性相关系数 越大,两个变量的线性相关性越强
的
D. 在残差 散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好
10. 下列说法正确的是( )
第2页/共5页
学科网(北京)股份有限公司A. 若 ,则 B. 的最小值为2
C. D. 的最小值为2
11. 已知无穷数列 中, 是以10为首项,以 为公差的等差数列, 是
以 为首项,以 为公式的等比数列 ,对一切正整数 ,都有 .设数列 的
前 项和为 ,则( )
A. 当 时, B. 当 时,
C. 当 时, D. 不存在 ,使得 成立
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知函数 的定义域为 ,则函数 的定义域为____________.
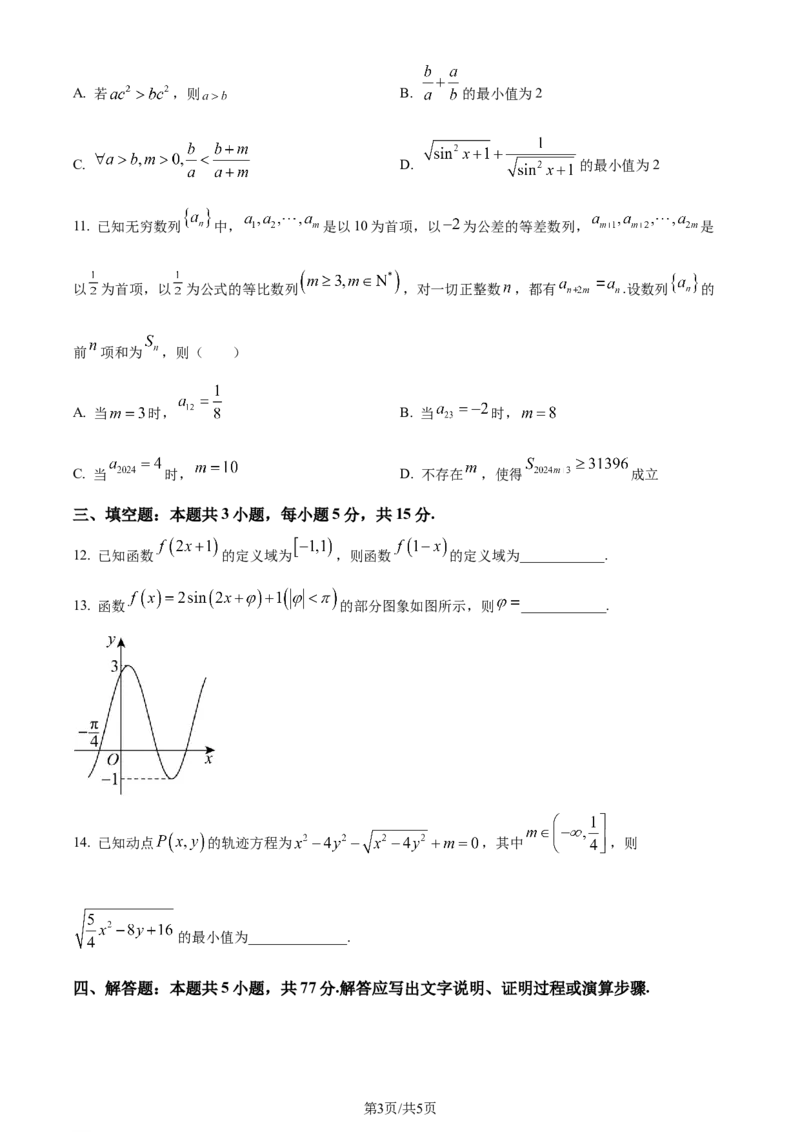
13. 函数 的部分图象如图所示,则 ____________.
14. 已知动点 的轨迹方程为 ,其中 ,则
的最小值为______________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
第3页/共5页
学科网(北京)股份有限公司15. 在 中,角 的对边分别为 ,已知 .
(1)求 ;
(2)已知 ,求 最的大值.
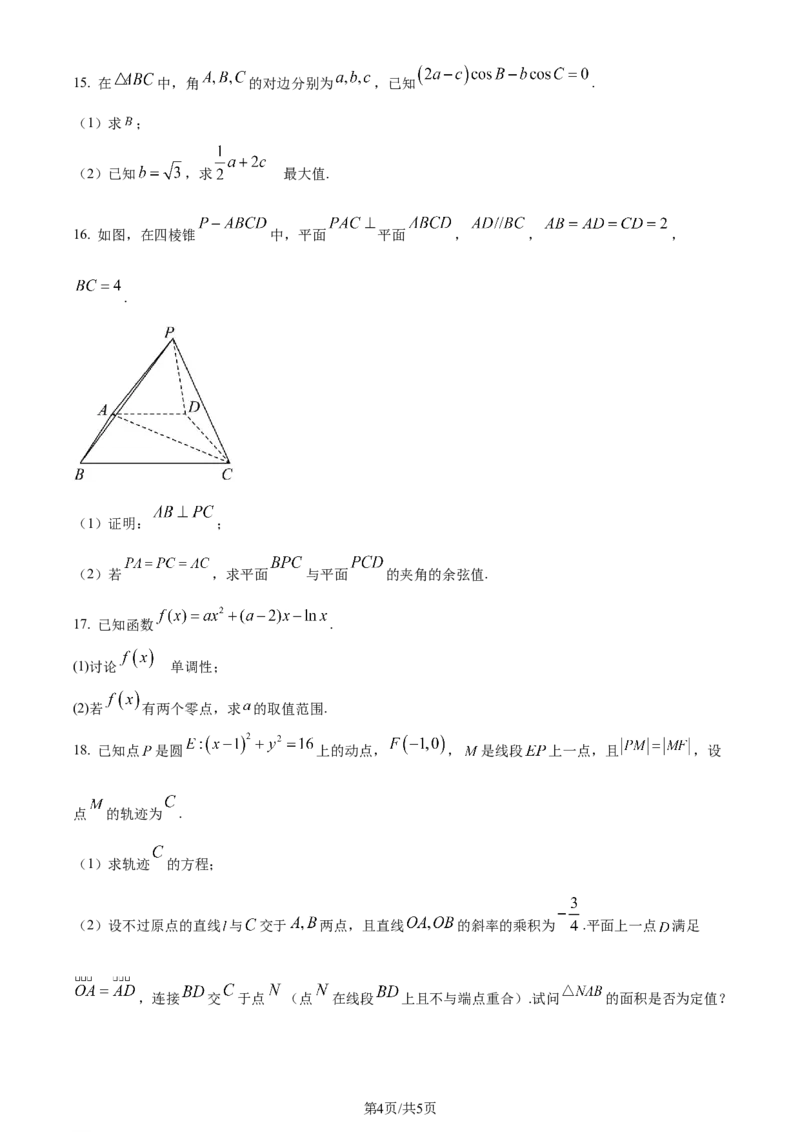
16. 如图,在四棱锥 中,平面 平面 , , ,
.
(1)证明: ;
(2)若 ,求平面 与平面 的夹角的余弦值.
17. 已知函数 .
的
(1)讨论 单调性;
(2)若 有两个零点,求 的取值范围.
18. 已知点 是圆 上的动点, , 是线段 上一点,且 ,设
点 的轨迹为 .
(1)求轨迹 的方程;
(2)设不过原点的直线 与 交于 两点,且直线 的斜率的乘积为 .平面上一点 满足
,连接 交 于点 (点 在线段 上且不与端点重合).试问 的面积是否为定值?
第4页/共5页
学科网(北京)股份有限公司若是,求出定值;若不是定值,说明理由.
19. 利用方程的方法可以将无限循环小数化为分数,例如将 化为分数是这样计算的:设 ,则
,即 ,解得 .
这是一种利用方程求解具有无限过程的问题的方法,这种方法在高中计算无限概率、无限期望问题时都有
很好的妙用.
已知甲、乙两人进行乒乓球比赛,每局比赛甲获胜的概率为 ,乙获胜的概率为 ,每局比赛的结果互不
影响.规定:净胜 局指的是一方比另一方多胜 局.
(1)如果约定先获得净胜两局者获胜,求恰好4局结束比赛的概率;
(2)如果约定先获得净胜三局者获胜,那么在比赛过程中,甲可能净胜 局.设甲
在净胜 局时,继续比赛甲获胜的概率为 ,比赛结束(甲、乙有一方先净胜三局)时需进行的局数为 ,
期望为 .
①求甲获胜的概率 ;
②求 .
第5页/共5页
学科网(北京)股份有限公司